Понятие модели и моделирования

1.

Понятие модели и моделирования
Процесс оптимизации транспортных систем –
отыскание
оптимальных
пропорций
между
количественными значениями и тенденциями
изменения
материальных,
технологических
и
организационных
факторов,
связанных
с
функционированием транспортных систем. Для
решения
таких
задач
необходимо
описать
количественные показатели транспортных систем
были бы связаны с экономическими математическим
соотношением.
Составление
таких
зависимостей
образует
математическую модель объекта исследования.

2.

Выделяют несколько классов задач
оптимизации транспортных систем:
•задачи маршрутизации перевозок и движения транспортных
средств – выбор рациональных или оптимальных схем
перемещения грузов и пассажиров между конечным числом
пунктов;
•задачи загрузки транспортных средств – определяют
номенклатуру, объем и схему размещения груза при перевозке;
•задачи составления графиков движения – обслуживание
технологических процессов производственных предприятий,
выполнение перевозок по технологии «точно в срок», при загрузке
или разгрузке транспортных средств на крупных терминалах и
складах, пассажирских перевозках;
•задачи планирования использования трудовых и технических
ресурсов в транспортном узле - составление согласованных
графиков работы всех видов транспорта с учетом их технических и
технологических особенностей, рационального распределения
объемов прямой и складской перевалки и т.д.

3.

Сущность моделирования заключается в замене реальной системы
некоторой другой искусственной системой более удобной для исследования.
После подобной замены исследуется прообраз, модель системы, и
результаты исследования распространяются на реальную систему.
Модель - это приближенное или упрощённое воспроизведение важнейших
сторон, особенностей и характеристик изучаемых систем, явлений и процессов.
Модели делятся на:
материальные – отображают оригинал за счет установления между ними определенного
подобия:
физическое (прямое) – модель воспроизводит изучаемый процесс с сохранением
изучаемых свойств (масштабные модели транспортных средств)
косвенное - совпадение или близость между оригиналом и абстрактной моделью
(часы – аналог времени, электрические схемы – аналог транспортных потоков, автопилот –
аналог летчика)
условное – достигаемое в результате соглашения (карты местности, удостоверение
личности)
абстрактные – создаются посредством мышления
внутренние – отражают механизм мышления и выражаются в языковых конструкциях
внешние – для коллективной деятельности (они бывают иррациональные – театральные
спектакли, и языковые – выражаются на естественном языке или в специальной знаковой
форме – формулы)
знаковые – материальные модели с абстрактным содержанием (к ним относят
информационные модели, или модели данных – это средство формирования
представления о данных, их составе и использовании в конкретных условиях)

4.

Необходимыми и достаточными признаками модели являются
следующие условия:
•между моделью и оригиналом имеется отношение сходства, форма которого
явно выражена и точно зафиксирована (условие отражения);
•модель в процессе научного познания является заместителем изучаемого
объекта (условие репрезентативности);
•изучение модели позволяет получить информацию об оригинале (условие
экстраполяции).
Модель никогда не бывает тождественна рассматриваемому
объекту или процессу, не передает всех его свойств и особенностей.
Основанная на упрощении, идеализации, она является его
приближенным отражением. Поэтому результаты, которые
получаются при анализе исследования модели, всегда носят для
объекта или процесса приближенный характер. Точность
результатов оценивается степенью соответствия объекта и его
модели, называемой адекватностью.

5.

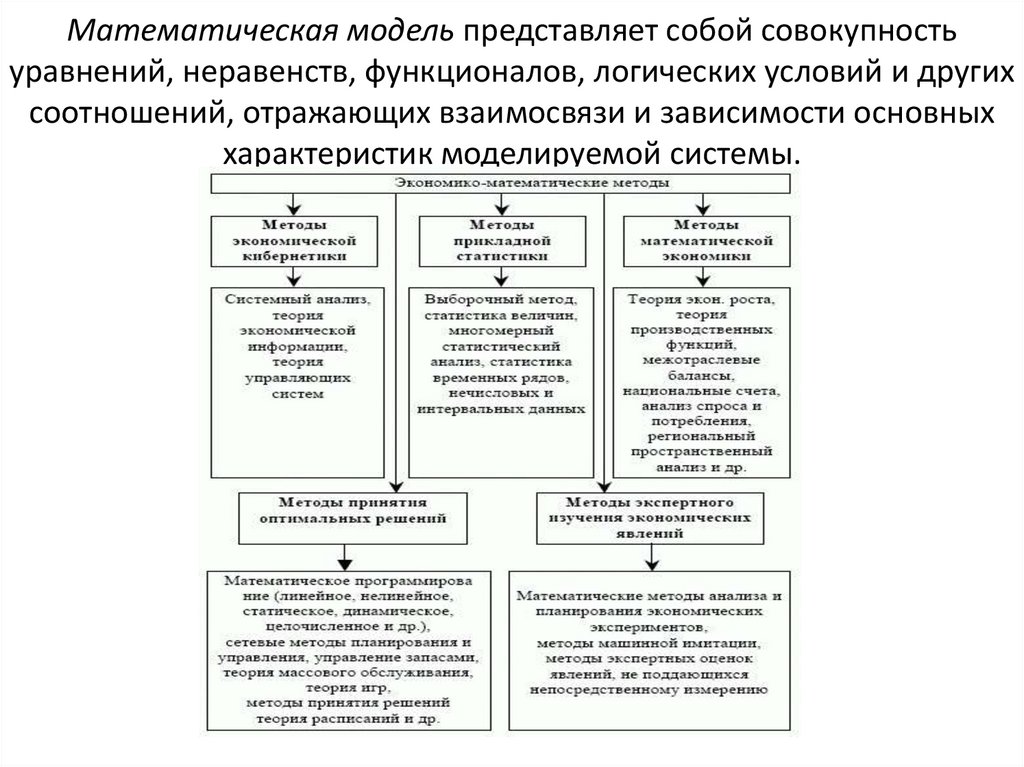
Математическая модель представляет собой совокупность
уравнений, неравенств, функционалов, логических условий и других
соотношений, отражающих взаимосвязи и зависимости основных
характеристик моделируемой системы.

6.

Особенности применения методов математического
моделирования в экономике:
Первая особенность связана с необходимостью при модельном
исследовании сохранить целостность системы.
Второй особенностью является отсутствие полностью однородных
объектов как на микро-, так и на макроуровнях, что затрудняет
перенос результатов исследований с одного объекта на другой.
Третьей особенностью является непрерывное изменение изучаемых
экономических объектов во времени. Динамический характер
процессов связан с изменением параметров и структуры
экономических систем, что требует периодической «поднастройки»
моделей.
Четвёртая особенность применения математического
моделирования в экономике связана с факторами случайности и
неопределенности.

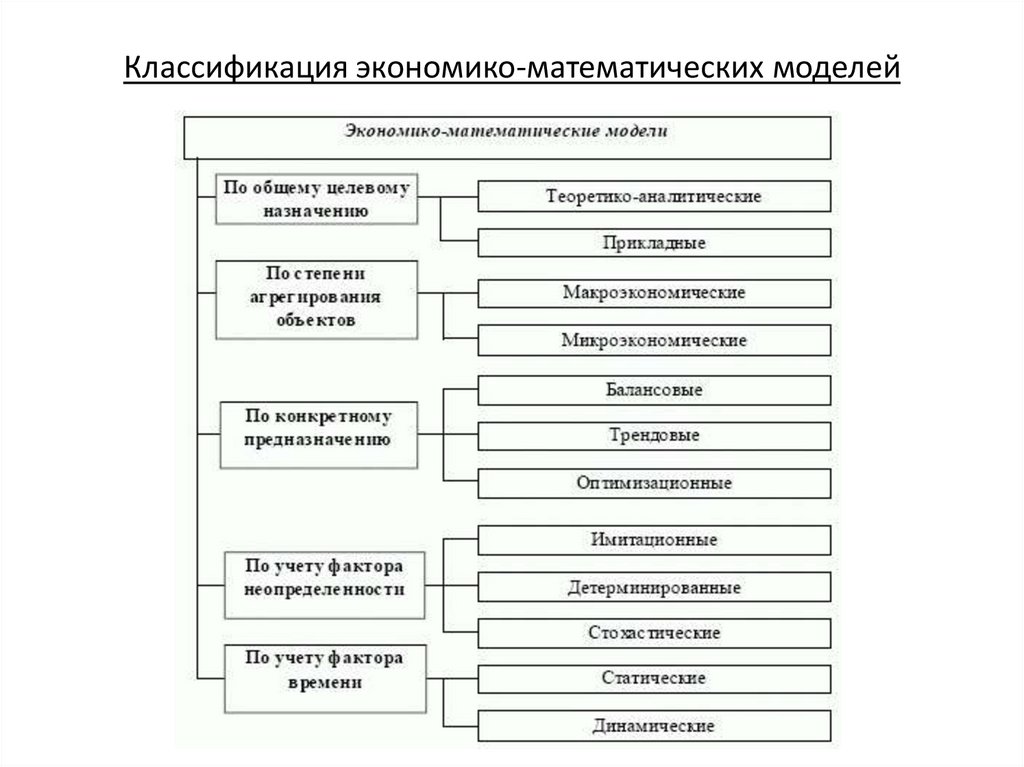
7.

Классификация экономико-математических моделей

8.

Процесс математического моделирования в общем
случае содержит следующее этапы:
•постановка задачи и описание ее содержания;
•сбор и обработка исходных данных, анализ полученной
информации с целью выявления наиболее существенных
и качественных взаимосвязей между факторами;
•построение экономико-математической модели в виде
системы уравнений и неравенств, определение функции
цели и систем ограничений;
•выбор в зависимости от характера модели численного
метода решения задачи, разработка или выбор
соответствующего вычислительного алгоритма
(машинной программы);
•выполнение расчетов и анализ результатов решения.

9.

Экономико-математические модели
обычно состоят из двух частей:
•ограничений задачи в виде набора независимых
переменных и условий, характеризующих их
приемлемые значения;
•целевой функции, которую необходимо
оптимизировать.
Поиск наилучшего решения обычно связан с
определением максимального или минимального
значения целевой функции в зависимости от
выбранного критерия оптимизации.

10.

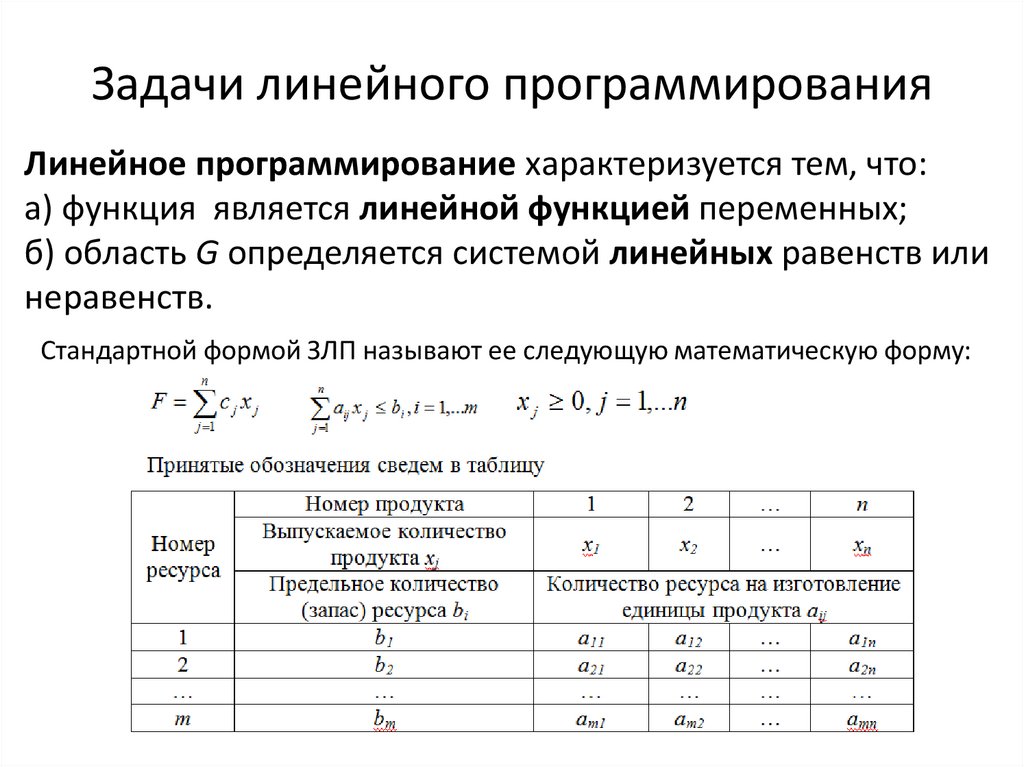
Задачи линейного программирования
Линейное программирование характеризуется тем, что:
а) функция является линейной функцией переменных;
б) область G определяется системой линейных равенств или
неравенств.
Стандартной формой ЗЛП называют ее следующую математическую форму:

11.

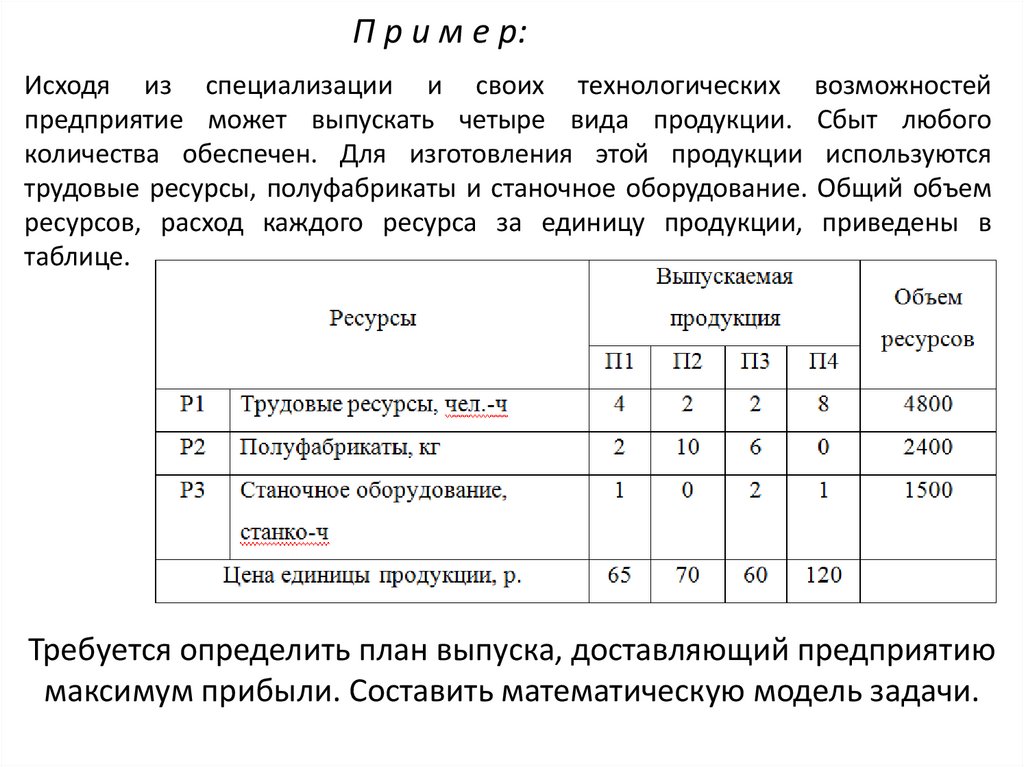
П р и м е р:
Исходя из специализации и своих технологических возможностей
предприятие может выпускать четыре вида продукции. Сбыт любого
количества обеспечен. Для изготовления этой продукции используются
трудовые ресурсы, полуфабрикаты и станочное оборудование. Общий объем
ресурсов, расход каждого ресурса за единицу продукции, приведены в
таблице.
Требуется определить план выпуска, доставляющий предприятию
максимум прибыли. Составить математическую модель задачи.

12.

П р и м е р:
Пусть
– объемы продукции
Z— сумма ожидаемой выручки.
Математическая модель задачи:
, планируемой к выпуску;

13.

Задача коммивояжера
Задача коммивояжера – задача математического программирования по
определению оптимального маршрута движения коммивояжера, цель которого
состоит в том, чтобы посетить все объекты, записанные в задании, за кратчайший
срок и с наименьшими затратами.
Задача коммивояжера формулируется очень просто: на плоскости (в
пространстве) расположены N городов, заданы расстояния между каждой парой
городов, требуется найти маршрут минимальной длины с посещением каждого
города ровно один раз и с возвращением в исходную точку.
Гамильтонов путь (или гамильтонова цепь) – путь (цепь), содержащий каждую
вершину графа ровно один раз.
Асимметричная задача коммивояжера отличается тем, что она моделируется
ориентированным графом. Таким образом, следует также учитывать, в каком
направлении находятся ребра.
Симметричная задача - все пары ребер между одними и теми же вершинами
имеют одинаковую длину. В симметричном случае количество возможных
маршрутов вдвое меньше асимметричного случая. Симметричная задача
моделируется неориентированным графом.

14.

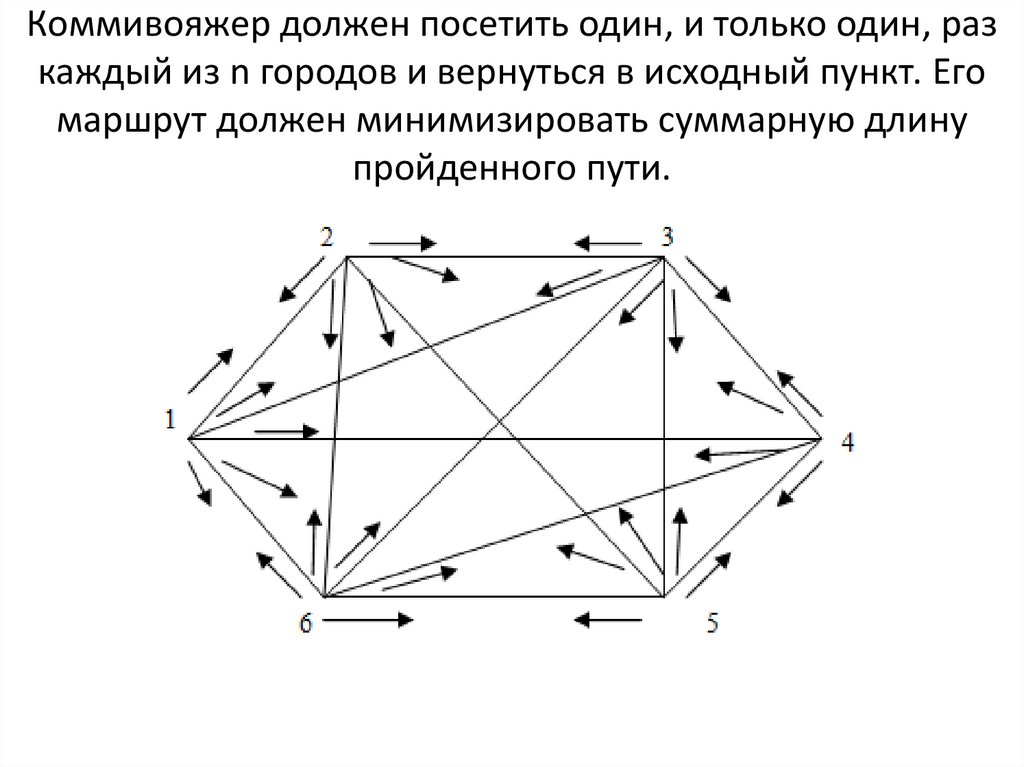
Коммивояжер должен посетить один, и только один, раз
каждый из n городов и вернуться в исходный пункт. Его
маршрут должен минимизировать суммарную длину
пройденного пути.

15.

В общем виде математическая постановка задачи
коммивояжера может быть сформулирована следующим
образом:

16.

Решение задачи коммивояжера (алгоритм Литтла)
Алгоритм Литтла – частный случай применения метода ветвей и
границ.
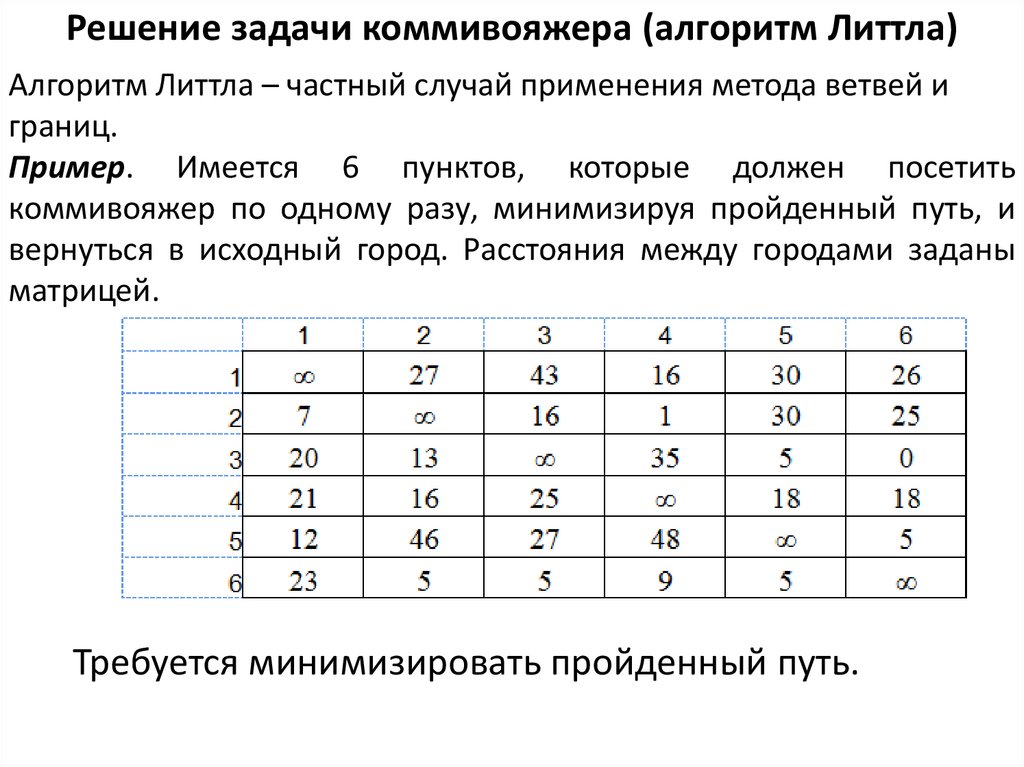
Пример. Имеется 6 пунктов, которые должен посетить
коммивояжер по одному разу, минимизируя пройденный путь, и
вернуться в исходный город. Расстояния между городами заданы
матрицей.
Требуется минимизировать пройденный путь.

17.

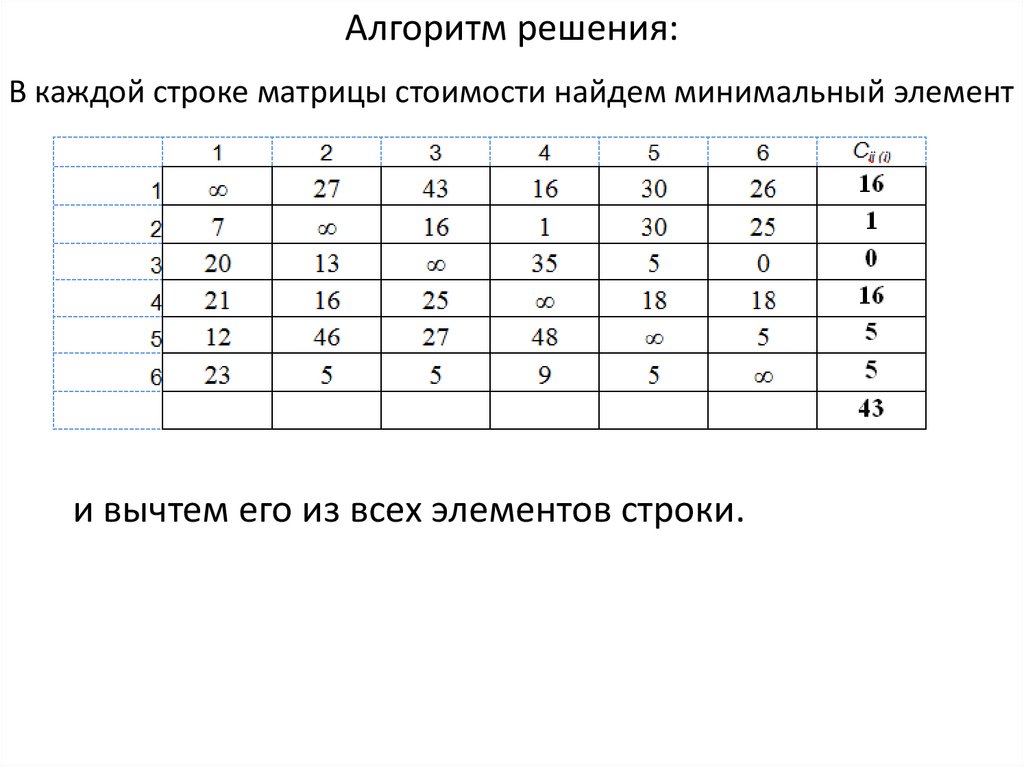
Алгоритм решения:
В каждой строке матрицы стоимости найдем минимальный элемент
и вычтем его из всех элементов строки.

18.

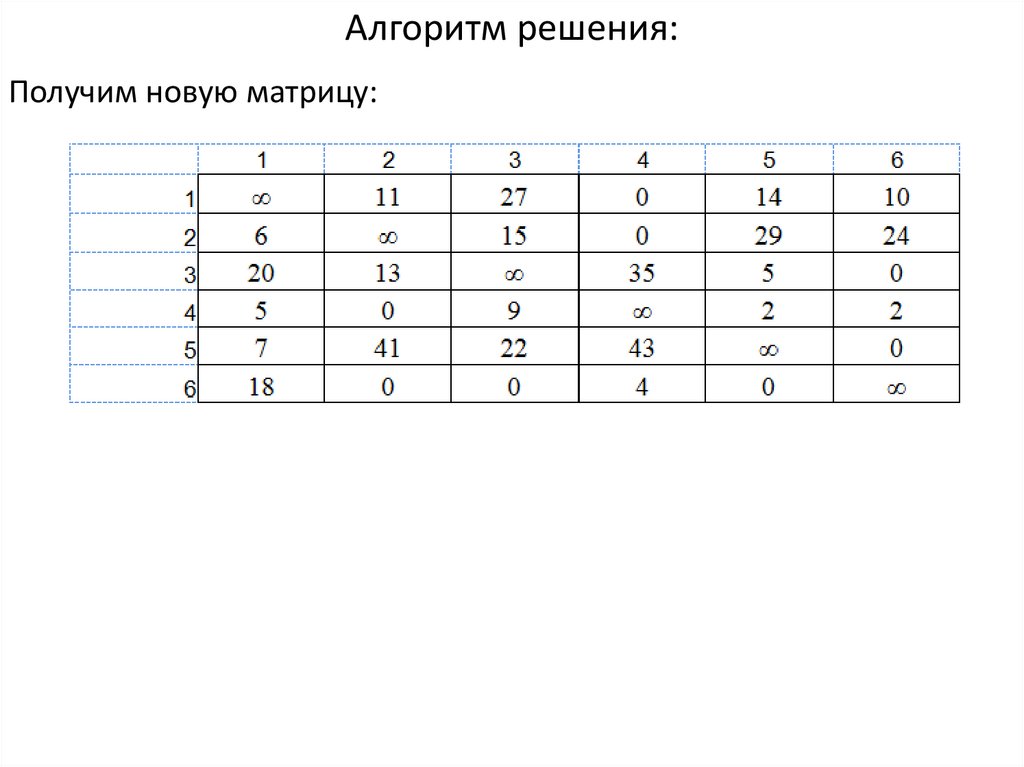
Алгоритм решения:
Получим новую матрицу:

19.

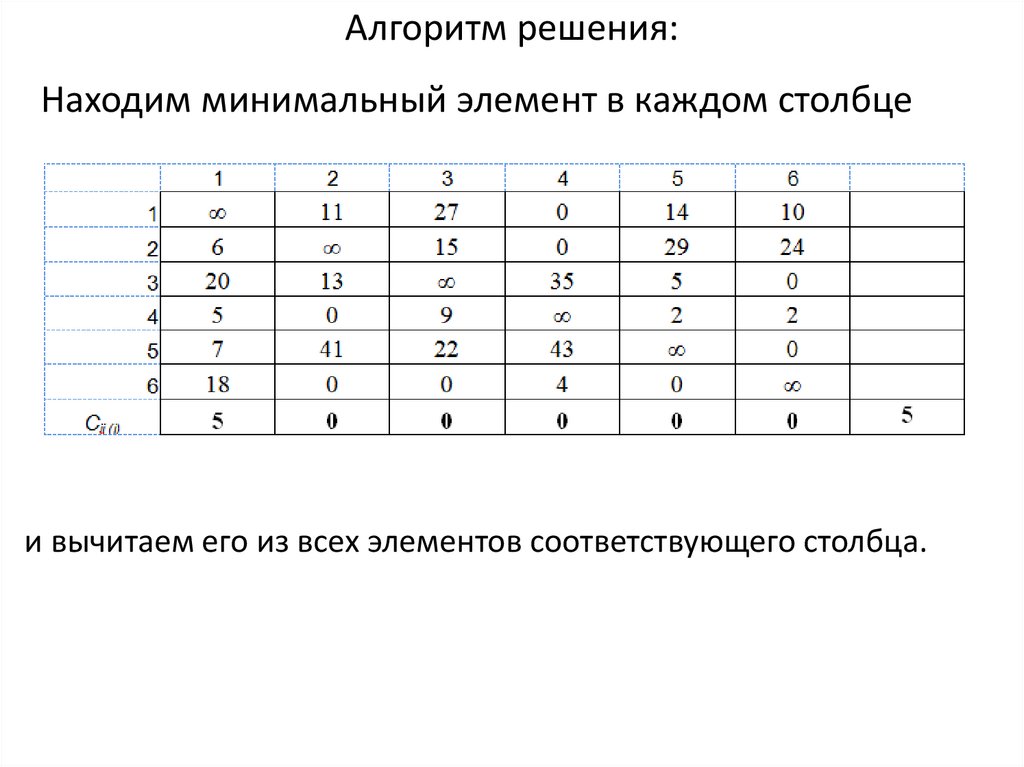
Алгоритм решения:
Находим минимальный элемент в каждом столбце
и вычитаем его из всех элементов соответствующего столбца.

20.

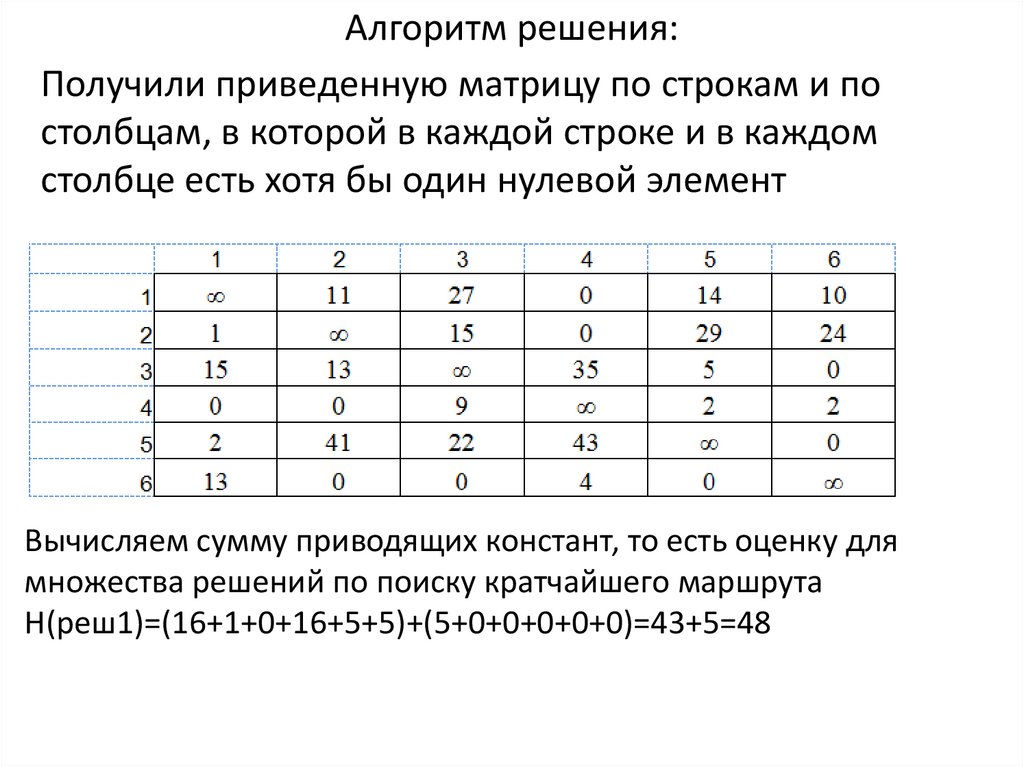
Алгоритм решения:
Получили приведенную матрицу по строкам и по
столбцам, в которой в каждой строке и в каждом
столбце есть хотя бы один нулевой элемент
Вычисляем сумму приводящих констант, то есть оценку для
множества решений по поиску кратчайшего маршрута
Н(реш1)=(16+1+0+16+5+5)+(5+0+0+0+0+0)=43+5=48

21.

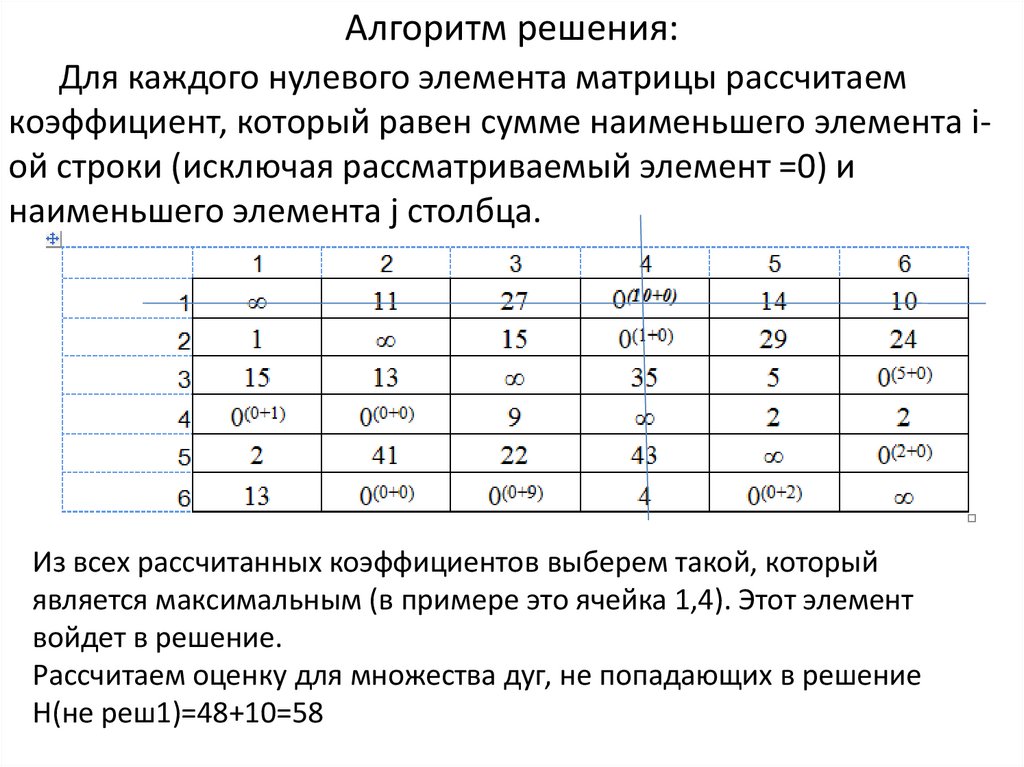
Алгоритм решения:
Для каждого нулевого элемента матрицы рассчитаем
коэффициент, который равен сумме наименьшего элемента iой строки (исключая рассматриваемый элемент =0) и
наименьшего элемента j столбца.
Из всех рассчитанных коэффициентов выберем такой, который
является максимальным (в примере это ячейка 1,4). Этот элемент
войдет в решение.
Рассчитаем оценку для множества дуг, не попадающих в решение
Н(не реш1)=48+10=58

22.

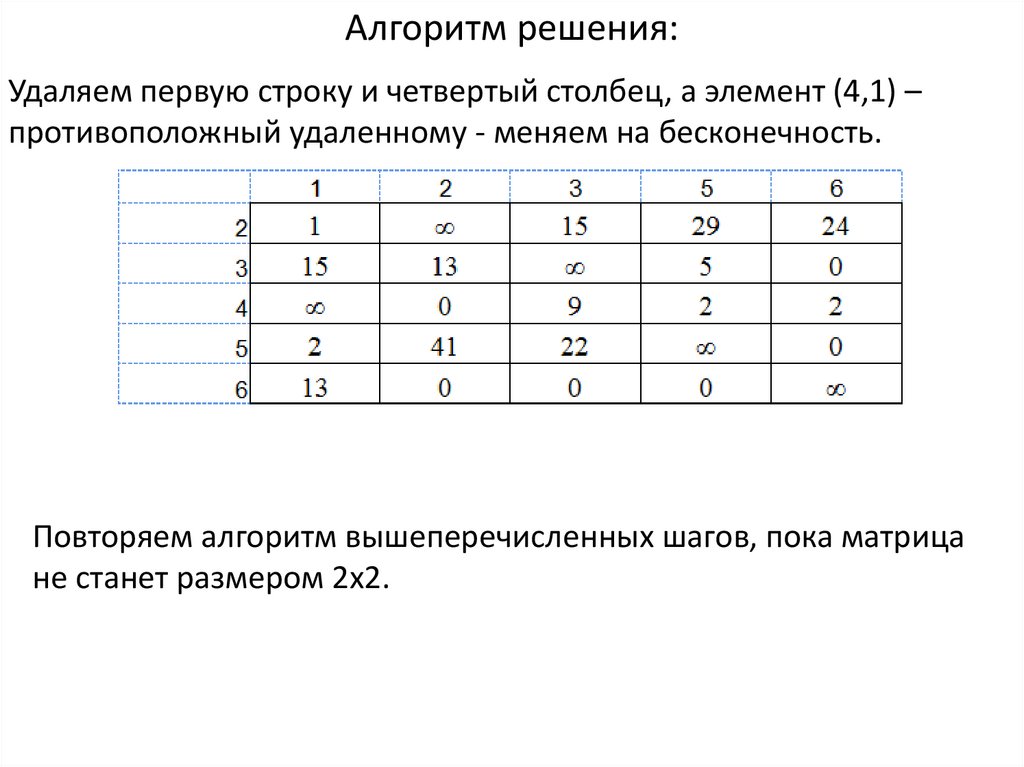
Алгоритм решения:
Удаляем первую строку и четвертый столбец, а элемент (4,1) –
противоположный удаленному - меняем на бесконечность.
Повторяем алгоритм вышеперечисленных шагов, пока матрица
не станет размером 2х2.

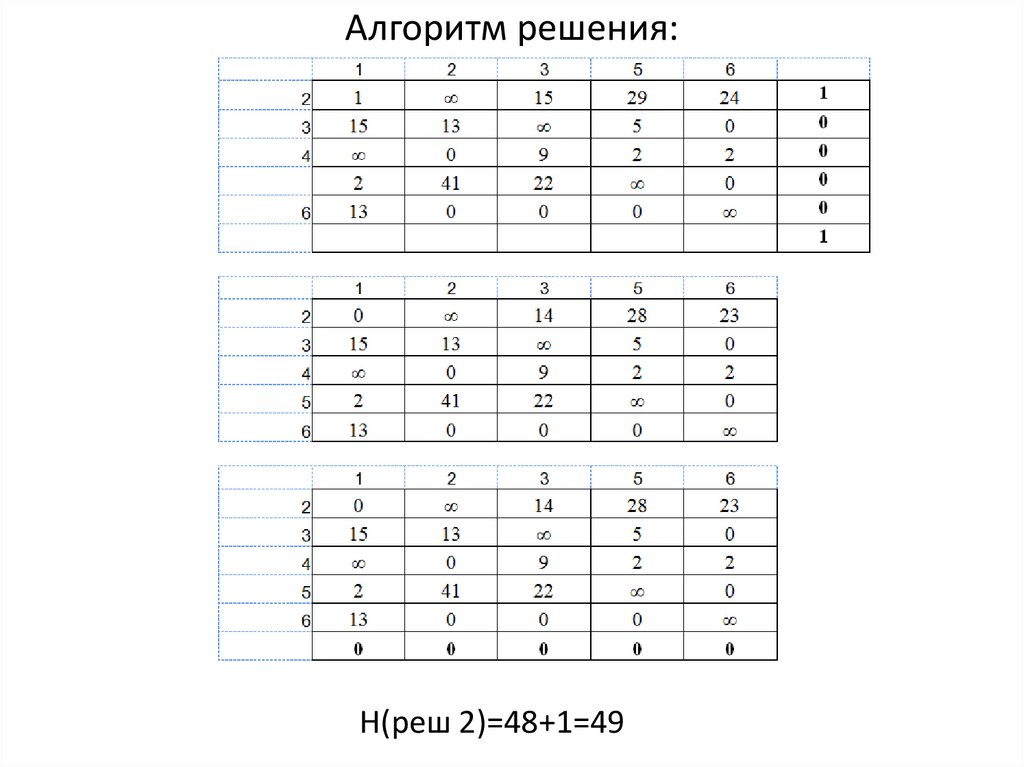
23.

Алгоритм решения:
Н(реш 2)=48+1=49

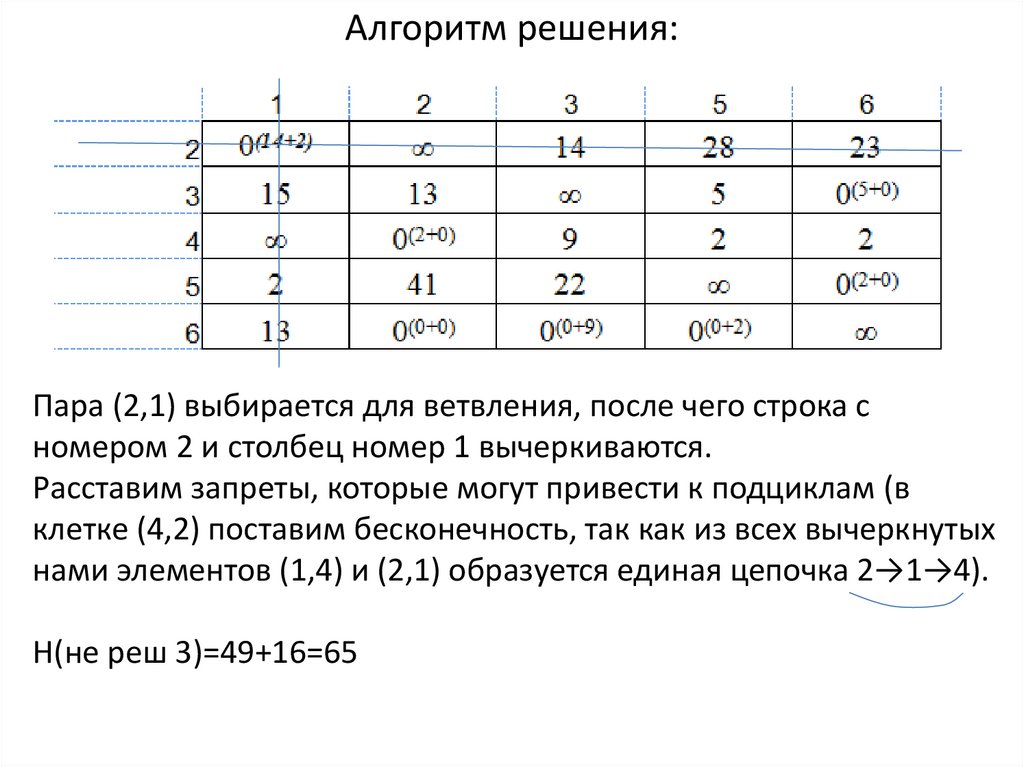
24.

Алгоритм решения:
Пара (2,1) выбирается для ветвления, после чего строка с
номером 2 и столбец номер 1 вычеркиваются.
Расставим запреты, которые могут привести к подциклам (в
клетке (4,2) поставим бесконечность, так как из всех вычеркнутых
нами элементов (1,4) и (2,1) образуется единая цепочка 2→1→4).
Н(не реш 3)=49+16=65

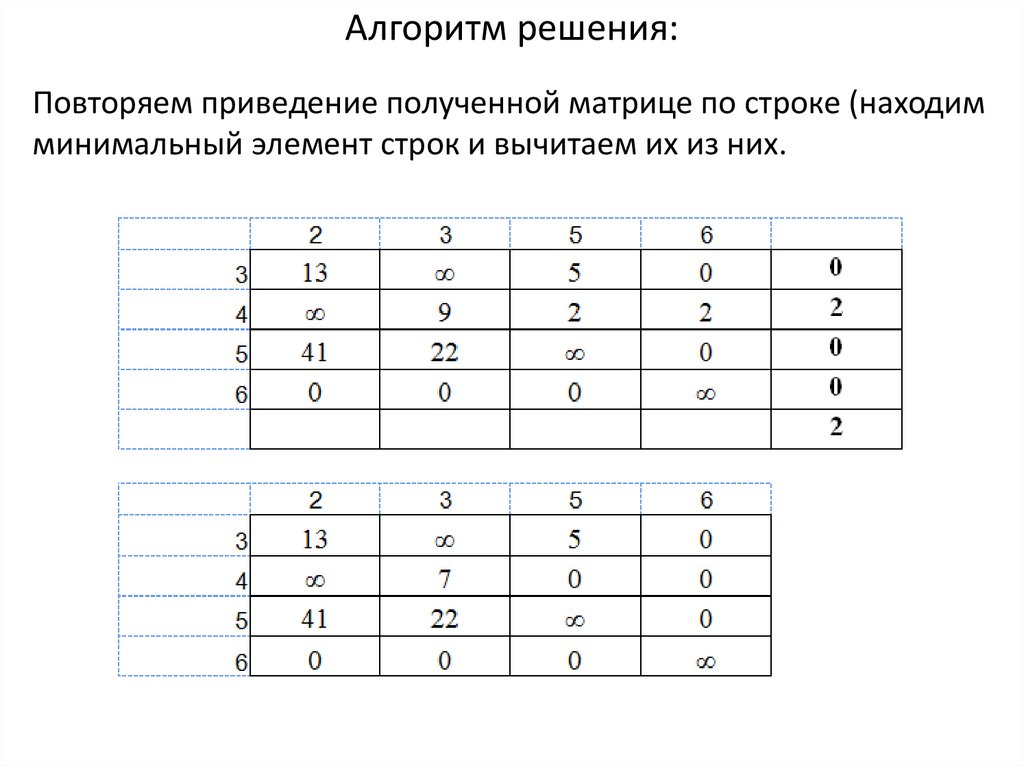
25.

Алгоритм решения:
Повторяем приведение полученной матрице по строке (находим
минимальный элемент строк и вычитаем их из них.

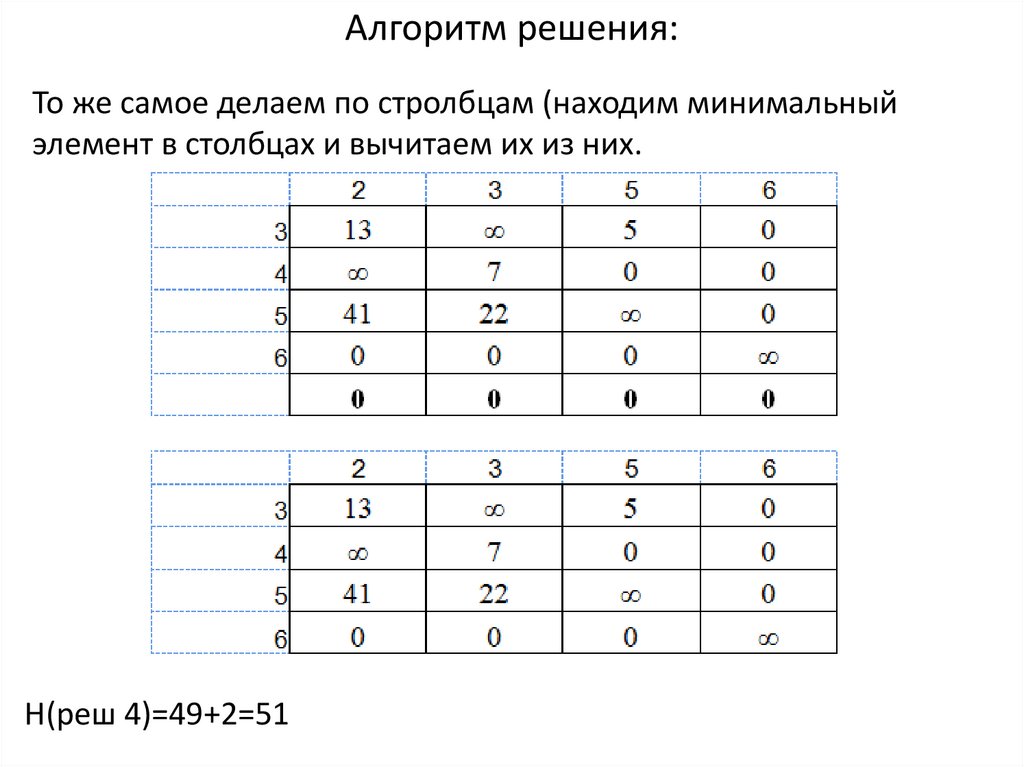
26.

Алгоритм решения:
То же самое делаем по стролбцам (находим минимальный
элемент в столбцах и вычитаем их из них.
Н(реш 4)=49+2=51

27.

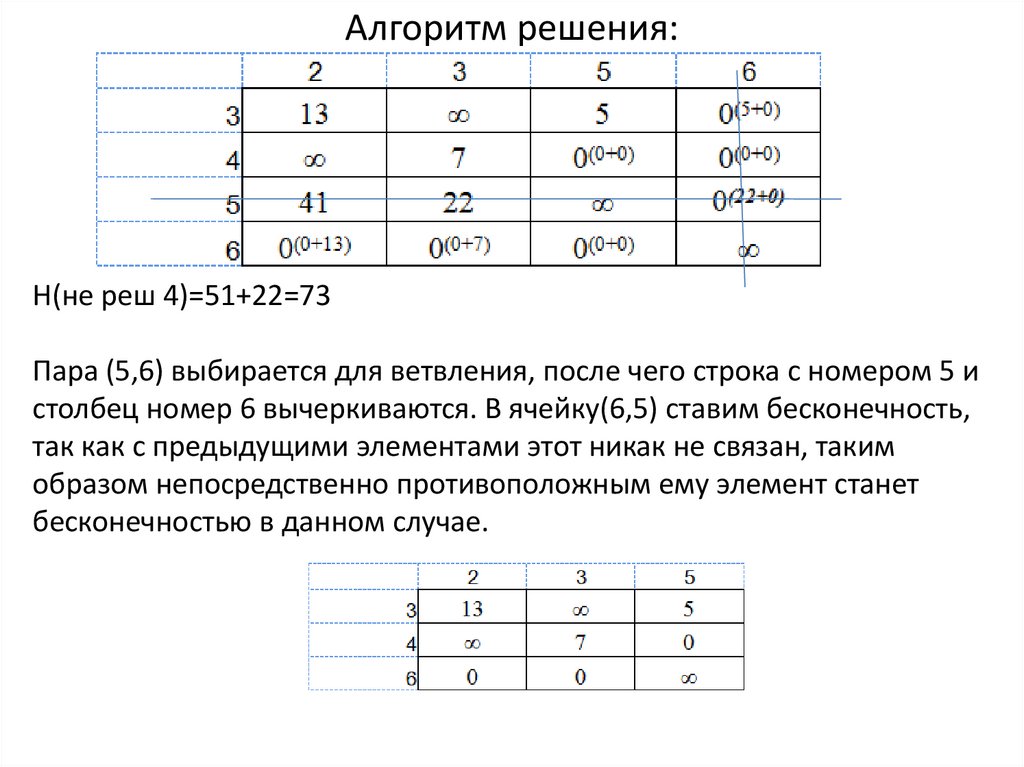
Алгоритм решения:
Н(не реш 4)=51+22=73
Пара (5,6) выбирается для ветвления, после чего строка с номером 5 и
столбец номер 6 вычеркиваются. В ячейку(6,5) ставим бесконечность,
так как с предыдущими элементами этот никак не связан, таким
образом непосредственно противоположным ему элемент станет
бесконечностью в данном случае.

28.

Алгоритм решения:
Н(реш 5)=51+5=56

29.

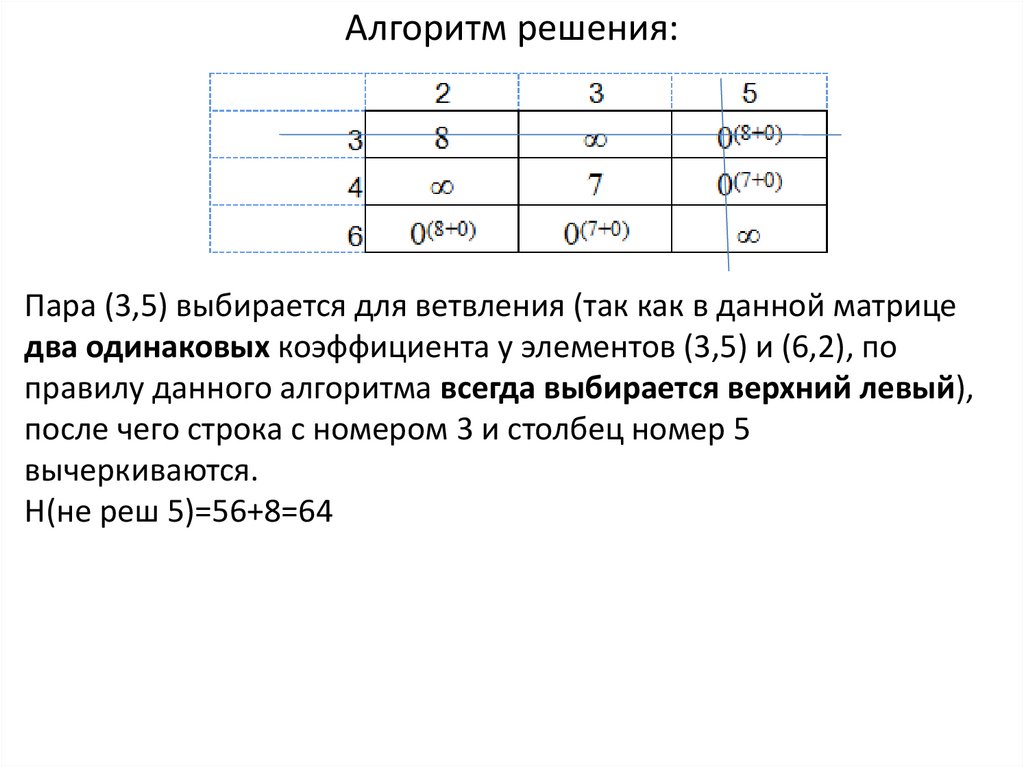
Алгоритм решения:
Пара (3,5) выбирается для ветвления (так как в данной матрице
два одинаковых коэффициента у элементов (3,5) и (6,2), по
правилу данного алгоритма всегда выбирается верхний левый),
после чего строка с номером 3 и столбец номер 5
вычеркиваются.
Н(не реш 5)=56+8=64

30.

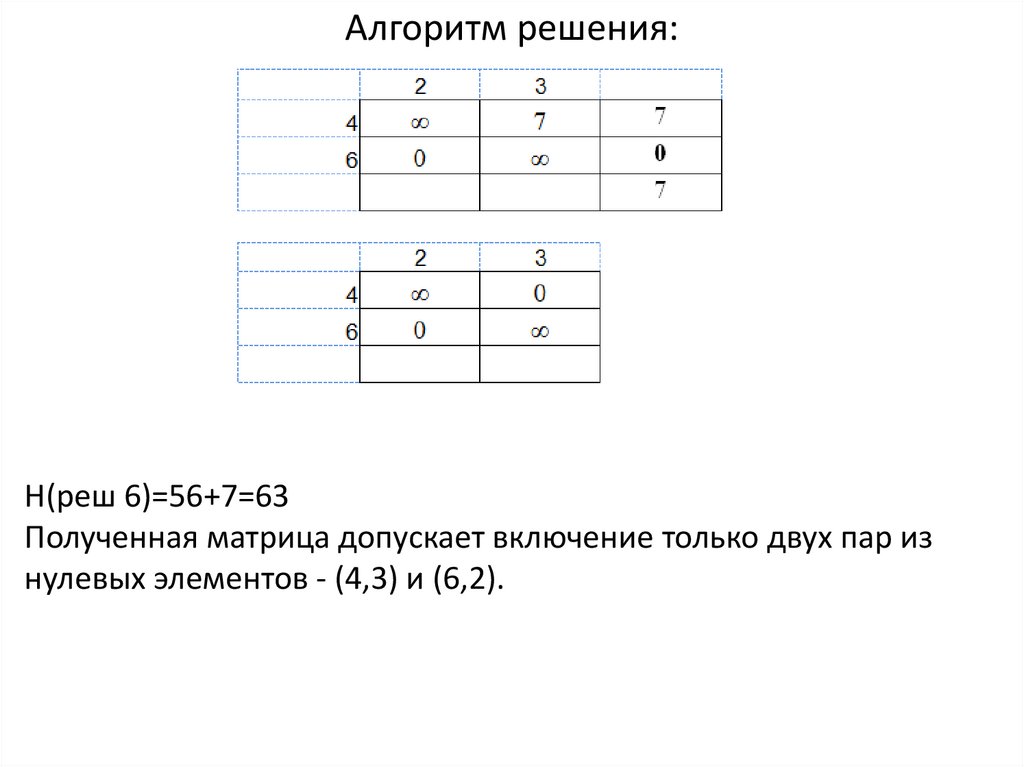
Алгоритм решения:
Н(реш 6)=56+7=63
Полученная матрица допускает включение только двух пар из
нулевых элементов - (4,3) и (6,2).

31.

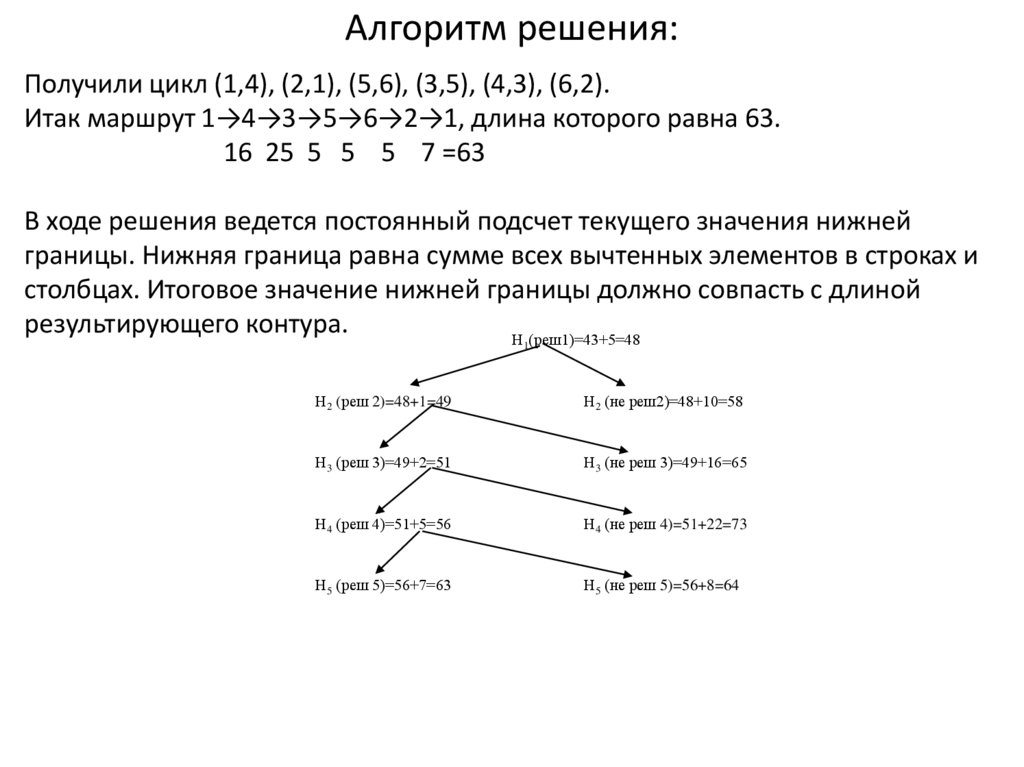
Алгоритм решения:
Получили цикл (1,4), (2,1), (5,6), (3,5), (4,3), (6,2).
Итак маршрут 1→4→3→5→6→2→1, длина которого равна 63.
16 25 5 5 5 7 =63
В ходе решения ведется постоянный подсчет текущего значения нижней
границы. Нижняя граница равна сумме всех вычтенных элементов в строках и
столбцах. Итоговое значение нижней границы должно совпасть с длиной
результирующего контура.
Н (реш1)=43+5=48
1
Н2 (реш 2)=48+1=49
Н2 (не реш2)=48+10=58
Н3 (реш 3)=49+2=51
Н3 (не реш 3)=49+16=65
Н4 (реш 4)=51+5=56
Н4 (не реш 4)=51+22=73
Н5 (реш 5)=56+7=63
Н5 (не реш 5)=56+8=64

32.

Методы нахождения опорных планов при решении
транспортных задач
Опорный план является допустимым решением ТЗ и используется в качестве
начального базисного решения при нахождении оптимального решения
методом потенциалов.
Существует четыре самых распространенных методов нахождения опорных
планов: метод северо-западного угла, метод минимального элемента, метод
двойного предпочтения и метод Фогеля.
«Качество» опорных планов, полученных этими методами, различается: в
общем случае метод Фогеля дает наилучшее решение (зачастую оптимальное),
а метод северо-западного угла – наихудшее.
Все существующие методы нахождения опорных планов отличаются только
способом выбора клетки для заполнения. Само заполнение происходит
одинаково независимо от используемого метода.
Следует помнить, что перед нахождением опорного плана транспортная задача
должна быть сбалансирована.

33.

Метод северо-западного угла
На каждом шаге метода северо-западного угла из всех не вычеркнутых клеток
выбирается самая левая и верхняя (северо-западная) клетка. Другими словами,
на каждом шаге выбирается первая из оставшихся не вычеркнутых строк и
первый из оставшихся не вычеркнутых столбцов.
Пункты
отправления,
А1
Пункты потребления,
В1
125
8
5
В4
1
130
2
ед. продукции
5
2
35
4
9
65
А3
ед. продукции
В3
85
5
А2
Потребность,
В2
Запасы,
9
125
2
90
3
130
1
100
целевая функция - общие затраты на перевозку составят
F
210
170
65

34.

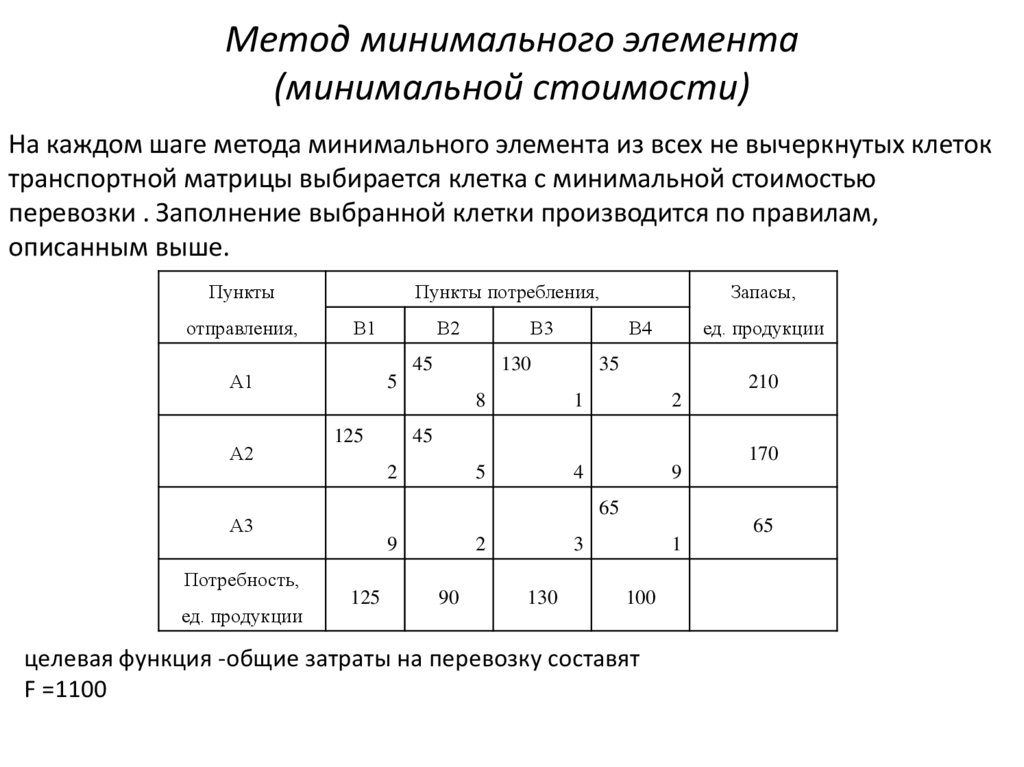
Метод минимального элемента
(минимальной стоимости)
На каждом шаге метода минимального элемента из всех не вычеркнутых клеток
транспортной матрицы выбирается клетка с минимальной стоимостью
перевозки . Заполнение выбранной клетки производится по правилам,
описанным выше.
Пункты
отправления,
Пункты потребления,
В1
А1
А2
5
125
ед. продукции
В3
45
В4
130
8
ед. продукции
35
1
2
45
2
5
4
9
65
А3
Потребность,
В2
Запасы,
9
125
2
90
3
130
1
100
целевая функция -общие затраты на перевозку составят
F =1100
210
170
65

35.

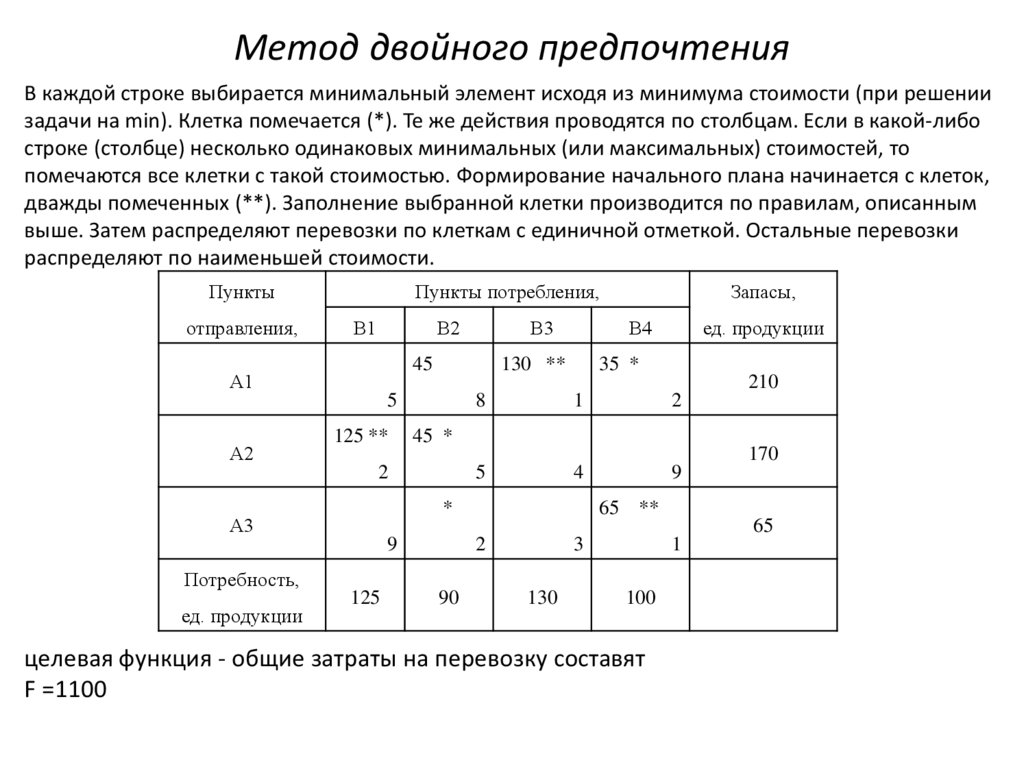
Метод двойного предпочтения
В каждой строке выбирается минимальный элемент исходя из минимума стоимости (при решении
задачи на min). Клетка помечается (*). Те же действия проводятся по столбцам. Если в какой-либо
строке (столбце) несколько одинаковых минимальных (или максимальных) стоимостей, то
помечаются все клетки с такой стоимостью. Формирование начального плана начинается с клеток,
дважды помеченных (**). Заполнение выбранной клетки производится по правилам, описанным
выше. Затем распределяют перевозки по клеткам с единичной отметкой. Остальные перевозки
распределяют по наименьшей стоимости.
Пункты
отправления,
Пункты потребления,
В1
В2
45
А1
А2
5
125 **
Потребность,
ед. продукции
В3
В4
130 **
35 *
8
1
5
2
4
*
9
125
ед. продукции
45 *
2
А3
Запасы,
65 **
2
90
9
3
130
1
100
целевая функция - общие затраты на перевозку составят
F =1100
210
170
65

36.

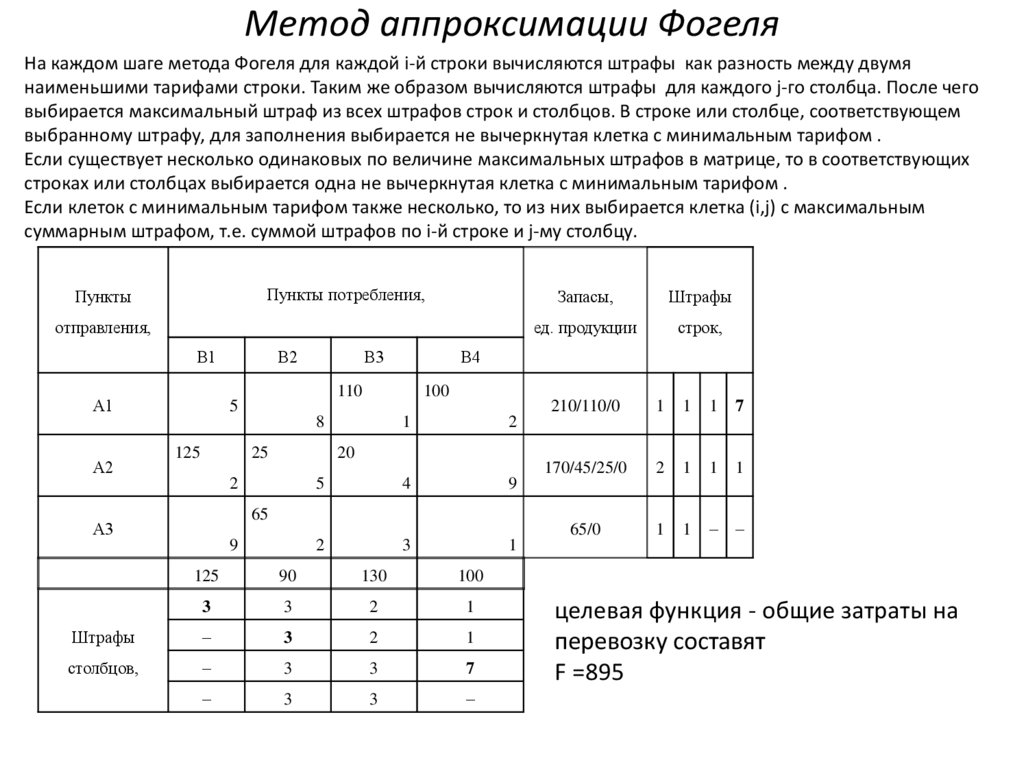
Метод аппроксимации Фогеля
На каждом шаге метода Фогеля для каждой i-й строки вычисляются штрафы как разность между двумя
наименьшими тарифами строки. Таким же образом вычисляются штрафы для каждого j-го столбца. После чего
выбирается максимальный штраф из всех штрафов строк и столбцов. В строке или столбце, соответствующем
выбранному штрафу, для заполнения выбирается не вычеркнутая клетка с минимальным тарифом .
Если существует несколько одинаковых по величине максимальных штрафов в матрице, то в соответствующих
строках или столбцах выбирается одна не вычеркнутая клетка с минимальным тарифом .
Если клеток с минимальным тарифом также несколько, то из них выбирается клетка (i,j) с максимальным
суммарным штрафом, т.е. суммой штрафов по i-й строке и j-му столбцу.
Пункты потребления,
Пункты
отправления,
В1
А1
В2
В3
100
8
А2
125
1
2
5
4
9
2
3
1
25
20
2
65
А3
9
Штрафы
ед. продукции
строк,
В4
110
5
Запасы,
125
90
130
100
3
3
2
1
Штрафы
–
3
2
1
столбцов,
–
3
3
7
–
3
3
–
210/110/0
1
1
1
7
170/45/25/0
2
1
1
1
65/0
1
1
–
–
целевая функция - общие затраты на
перевозку составят
F =895