Похожие презентации:
Фрагменты
1.
Фрагменты• «Кусок» стандартной схемы со свободными
дугами, многовходовая схема.
• Без операторов старт.
• Все дуги занумерованы
• Номера входных дуг уникальны
• Для входных дуг – множество результатов
(аналог старт) (есть много точек входа)
• Для выходных дуг – множество аргументов
(аналог стоп)
2.
Фрагменты - пример1
3
4 {x,y}
{x,y}
x := x
2
{x}
y := h(x)
{x}
2
{y}
• вход(G) =
{1,3,4}
• выход(G) = {2}
3.
Сужение фрагмента• Сужение фрагмента G[i o] –
стандартная схема, в которой
начальный оператор совпадает со
входом i вход(G), заключительный
оператор – с выходом o выход(G) { },
где означает «ни один из выходов
G».
4.
Сужение фрагмента• Случай i вход(G), o выход(G)
старт(x,y)
{x,y}
i
стоп(x,y)
петля
стоп(x)
петля
o
o
стоп(x)
{x}
{x,y}
стоп(x,y)
петля
5.
Сужение фрагмента• Случай i вход(G), o
старт(x,y)
{x,y}
i
стоп(x,y)
стоп(x)
петля
петля
петля
6.
Эквивалентность фрагментовФрагменты G1 и G2 эквивалентны, если
1. вход(G1) = вход(G2)
2. вход(G1) выход(G2) = ,
вход(G2) выход(G1) =
3. выходы с одинаковыми номерами имеют
одинаковые аргументы в обоих фрагментах
4. i вход(G1) o выход(G1) выход(G2) { } :
G1[i o] эквивалентно G2[i o]
Для любой эквивалентности:
функциональной, логико-термальной, ...
7.
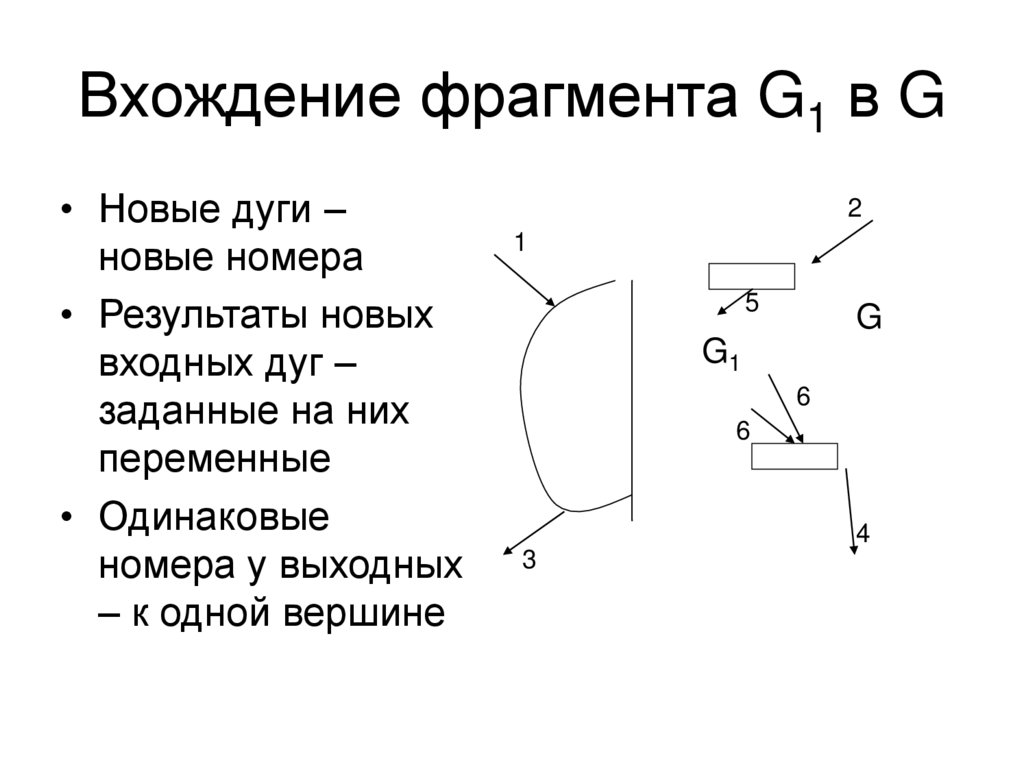
Вхождение фрагмента G1 в G• Новые дуги –
новые номера
• Результаты новых
входных дуг –
заданные на них
переменные
• Одинаковые
номера у выходных
– к одной вершине
2
1
5
G
G1
6
6
4
3
8.
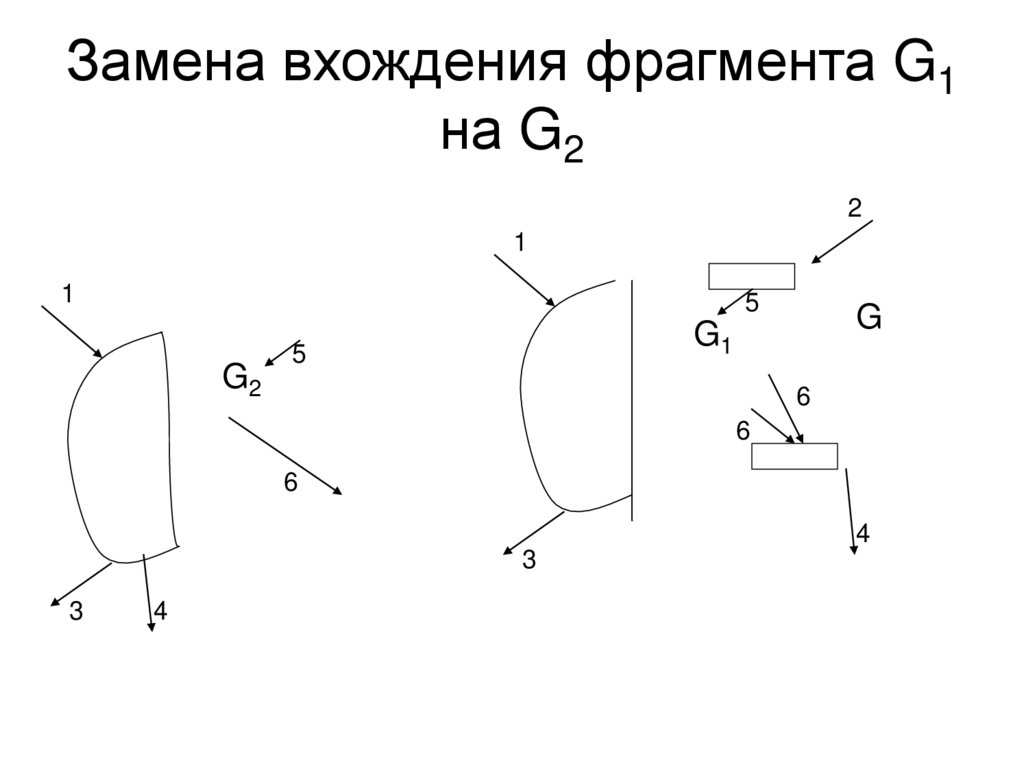
Замена вхождения фрагмента G1на G2
2
1
1
5
G2
G
G1
5
6
6
6
4
3
3
4
9.
Система преобразований• Правило преобразования – пара
эквивалентных фрагментов G1 G2
• Применение правила к фрагменту G –
замена в G фрагмента G1 на G2 (или
наоборот).
• Пример:
1
x := x
2
1
2
10.
Система преобразований• Схема правила – разрешимое
множество правил
• Применение схемы правила –
применение одного из правил
• Пример:
1
…
n
1
…
петля
n
11.
Система преобразований• Вывод в системе (схем) правил –
последовательность фрагментов G1,G2,…,Gn,
где Gi+1 получается из Gi применением схемы
правила из .
• Если существует вывод G1,G2,…,Gn, то
фраменты G1 и Gn называются
–равносильными – G1 Gn.
• Система называется полной для
эквивалентности ≈, если G1≈G2 G1 G2
• Система корректна относительно
эквивалентности ≈, если G1 Gn G1≈G2
12.
Система лт• ЛТ1) Удаление недостижимых
• ЛТ2) Стягивание тупиков
• ЛТ3) Копирование
• ЛТ4) Замена переменных
• ЛТ5) Удаление неиспользуемых
преобразователей
• ЛТ6) Удаление неиспользуемого входа
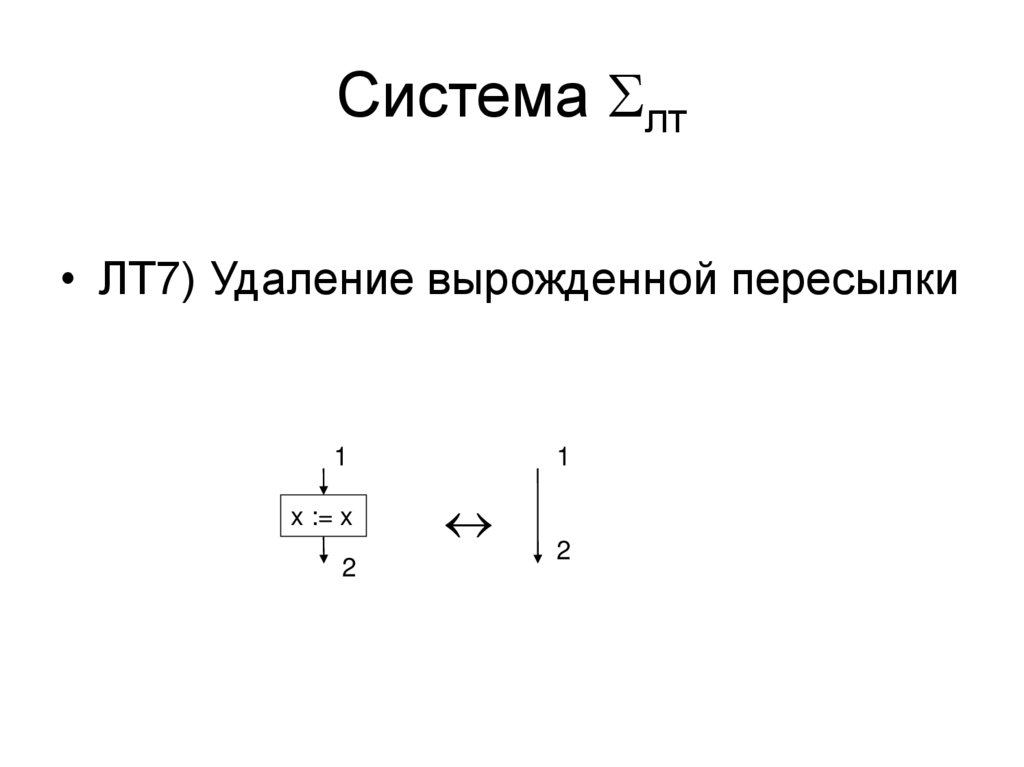
• ЛТ7) Удаление вырожденной пересылки
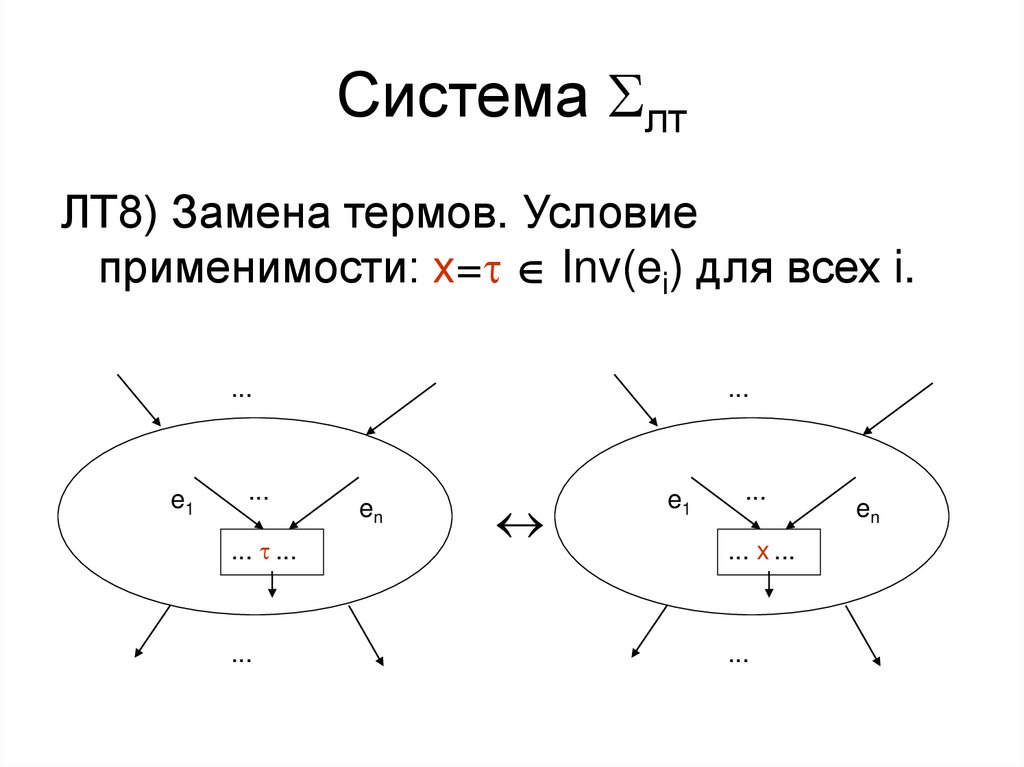
• ЛТ8) Замена термов
13.
Система лт• ЛТ1) Удаление недостижимых
нет входов
пусто
...
Необходим
глобальный
анализ
14.
Система лт• ЛТ2) Стягивание тупиков
...
...
петля
нет выходов
Необходим глобальный анализ
15.
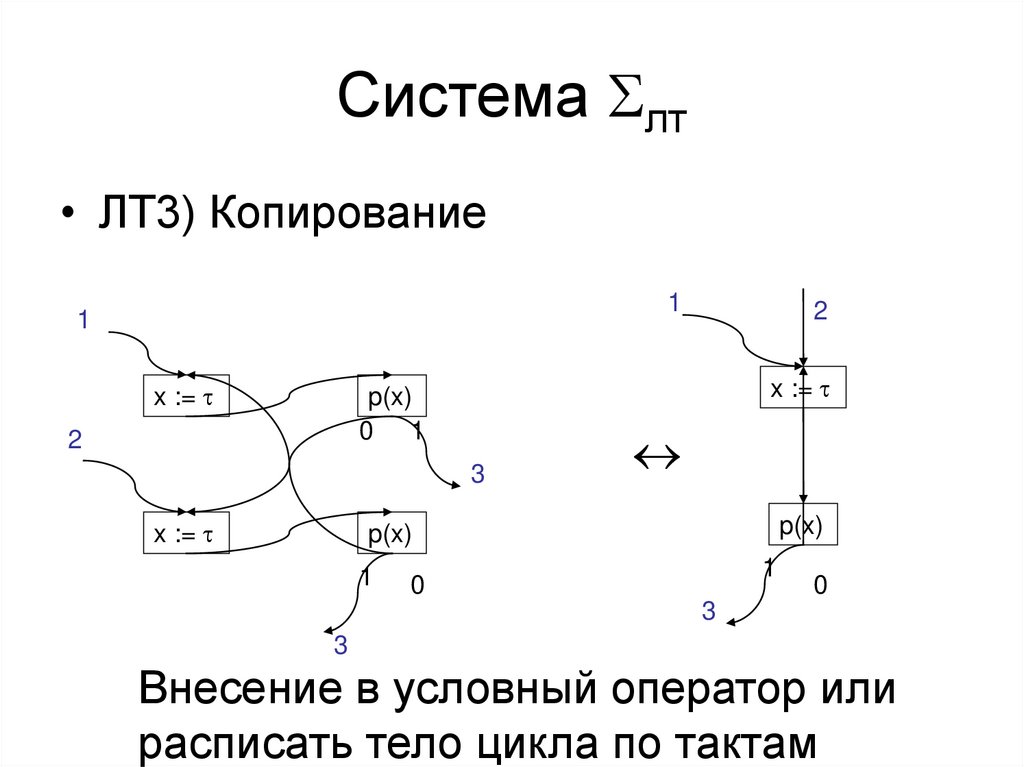
Система лт• ЛТ3) Копирование
1
1
x :=
x :=
p(x)
0 1
2
3
x :=
2
p(x)
p(x)
1
1
0
0
3
3
Внесение в условный оператор или
расписать тело цикла по тактам
16.
используетСистема лт информацинон
ный граф
• ЛТ4) Замена переменных: все
вхождения x заменить на y.
Условия применимости:
– ни один информационный маршрут x не
зацеплен ни с одним информационным
маршрутом y.
– x и y не являются результатами входов и
аргументами выходов
17.
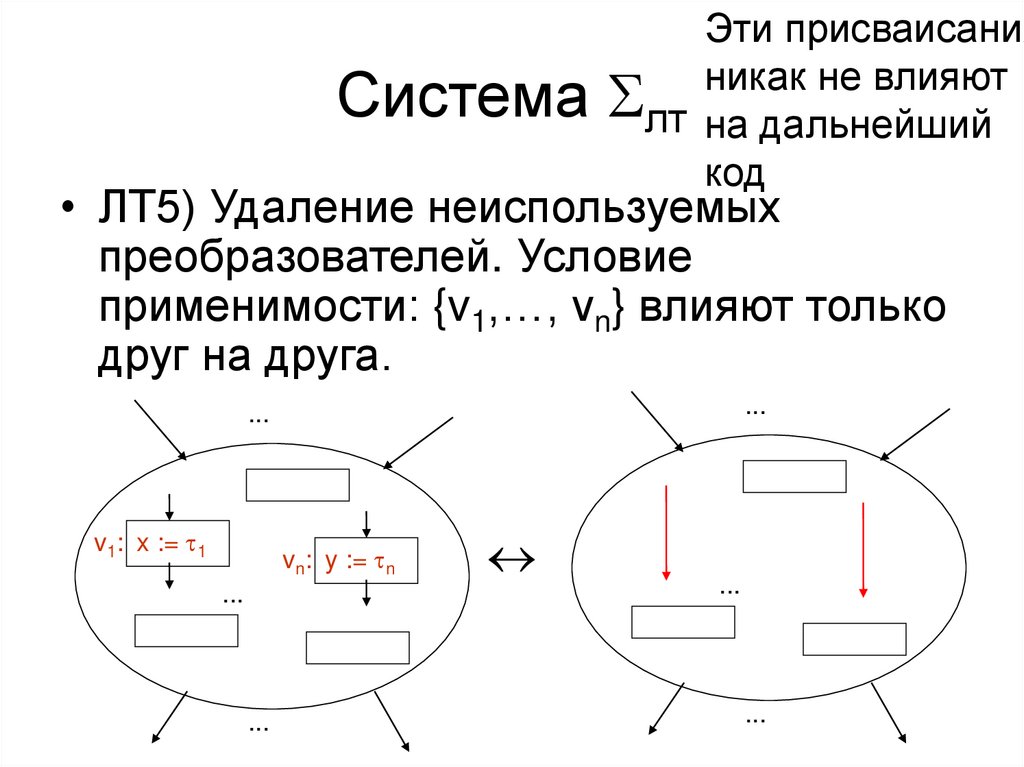
Эти присваисанияникак не влияют
Система лт на дальнейший
код
• ЛТ5) Удаление неиспользуемых
преобразователей. Условие
применимости: {v1,…, vn} влияют только
друг на друга.
...
...
v1: x := 1
vn: y := n
...
...
...
...
18.
Система лт• ЛТ6) Удаление неиспользуемого входа.
Условие применимости: от результата
x нет ни одной информационной
зависимости.
{x, … }
{…}
...
...
19.
Система лт• ЛТ7) Удаление вырожденной пересылки
1
x := x
2
1
2
20.
Система лтЛТ8) Замена термов. Условие
применимости: x= Inv(ei) для всех i.
...
e1
...
... ...
...
...
en
e1
...
... x ...
...
en
21.
Корректность• Теорема. Система лт корректна
относительно эквивалентности ≈лт:
G1 лт Gn G1≈лт G2
• Доказательство. Достаточно
проверить, что ни одно из
преобразований не меняет множество
лт-историй фрагмента. (Упражнение)
• Конец доказательства.
Множество
маршрутов от старта
22.
ПолнотаТеорема. Система лт полна для
эквивалентности ≈: G1≈лтG2
G1 лтG2
Доказательство. Построим процедуру
распознавания ≈лт путём
преобразовния G1 и G2 к одному и
тому же фрагменту:
1. Gi лт Fi : Fi - приведённый (не
зависимо)
2. Fi лт Hi : H1 согласован с H2
3. H1 лт H2
23.
Приведённые фрагменты• Фрагмент называется приведённым, если
– Любая вершина на пути от входа (ЛТ1 – удаление
недостижимых)
– От любой вершины есть путь к выходу (ЛТ2 – удаление
тупиков)
– К любому не распознавателю ровно одна дуга (ЛТ3 —
копирование) (этого нет тк мы удалили тупики, нет цикла
только с присваиваниями )
– В распознавателях и заключительных операторах – только
переменные (ЛТ5 – вставка неиспользуемых, ЛТ8 – замена
термов)
– Результаты входов не пересекаются с результатами
преобразователей (ЛТ7 – пустая пересылка, ЛТ4 – замена
пременных)
• Лемма. G F - приведённый : G лтF (это пункт 1)
24.
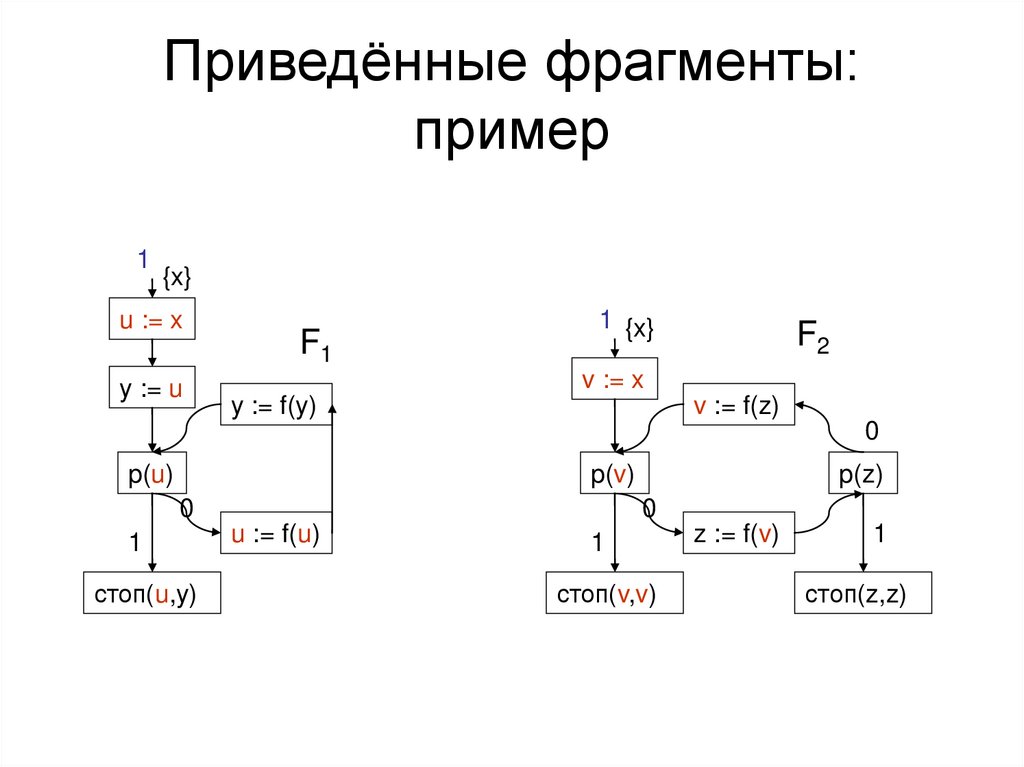
Приведённые фрагменты:пример
Все требования вып.,
кроме последнего
1
{x}
G2
G1
y := x
y := f(y)
1 {x}
x := f(z)
0
p(x)
p(x)
0
1
стоп(x,y)
p(z)
0
x := f(x)
1
стоп(x,x)
z := f(x)
1
стоп(z,z)
25.
Приведённые фрагменты:пример
1
{x}
u := x
y := u
F1
1 {x}
F2
v := x
y := f(y)
v := f(z)
0
p(u)
p(v)
0
1
стоп(u,y)
p(z)
0
u := f(u)
1
стоп(v,v)
z := f(v)
1
стоп(z,z)
26.
Согласованные фрагменты• Л-граф приведённого фрагмента:
– преобразователи заменяются дугой
– в распознавателях и операторах стоп
удаляются аргументы
– результаты (аргументы) входов (выходов)
удаляются
У нас уже все операторы имеют только
одну дугу, коме распознавателя
27.
1Л-граф – пример
{x}
u := x
y := u
1 {x}
F1
F2
v := x
y := f(y)
v := f(z)
0
p(u)
p(v)
0
1
0
u := f(u)
z := f(v)
1
стоп(u,y)
стоп(v,v)
1
{x}
p(z)
стоп
стоп(z,z)
1
Эквив
p
1
1
0
0
p
1
стоп
p
0
1
стоп
28.
Эквивалентность Л-графов• Разбиваем на классы эквивалентных вершин
(аналогично проверке эквивалентности
конечных автоматов): если не удалось –
фрагменты не эквивалентны.
1
1
0
p
1
стоп
0
p
1
стоп
p
0
1
стоп
29.
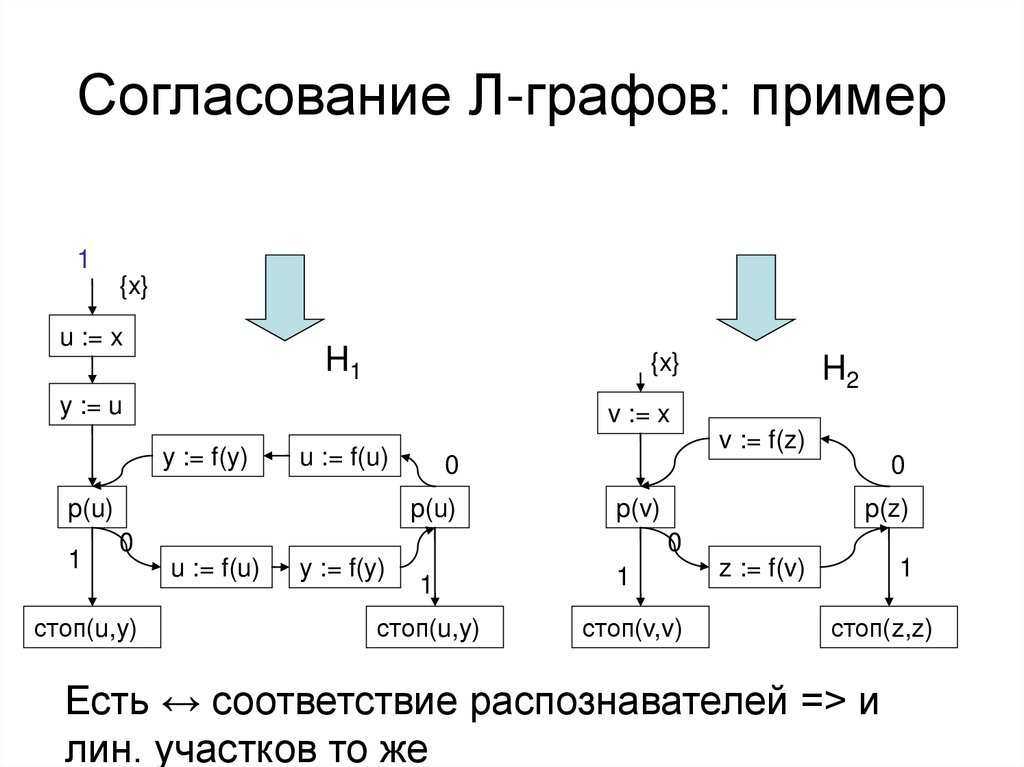
Согласование Л-графов5 и 7 => 35 и 35
• Каждая вершина-распознаватель
копируется (ЛТ3) столько раз, сколько
есть эквивалентных ей в другой схеме.
• Линейные участки (лучи,
последовательности
преобразователей) ведут к
соответствующим копиям.
Далее вернёмся от Л-графов
обратно
30.
Согласование Л-графов: пример1
{x}
u := x
H1
{x}
y := u
v := x
y := f(y)
v := f(z)
u := f(u)
p(u)
1
0
p(u)
0
p(v)
0
стоп(u,y)
H2
p(z)
0
u := f(u)
y := f(y)
1
1
стоп(u,y)
стоп(v,v)
z := f(v)
1
стоп(z,z)
Есть ↔ соответствие распознавателей => и
лин. участков то же
31.
Согласование фрагментов• Фрагменты согласованы, если
– Л-графы совпадают (уже есть)
– Множество результатов соответствующих входов
совпадает (ЛТ6 – неиспользуемые входы)
– Если есть оператор x:= в одном фрагменте, то x
не используется в другом (ЛТ4 – замена
пременных)
• Лемма. приведённых F1,F2 : Л-графы F1 и
F2 эквивалентны => H1,H2 : F1 лтH1 &
F2 лтH2 & H1 согласован с H2
32.
Доказательство теоремы• Пусть H1 и H2 согласованы. Скопируем
(ЛТ6 – вставка неиспользуемого) за
каждым лучом в H1 соответствующий
луч из H2
33.
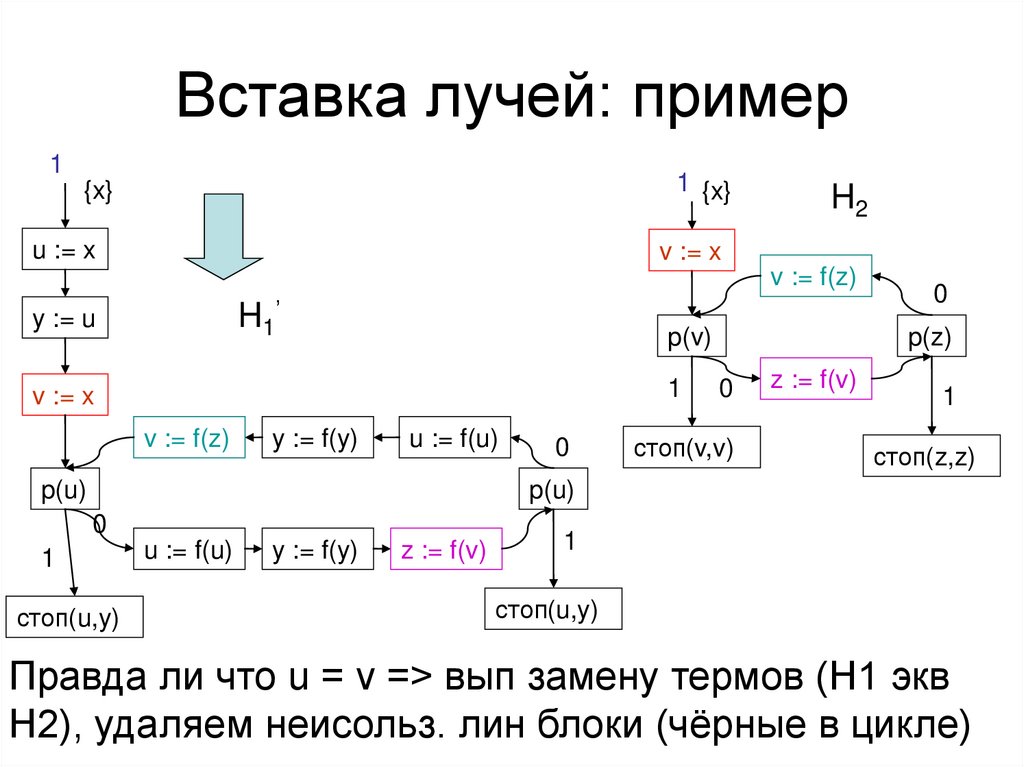
Вставка лучей: пример1
{x}
1 {x}
u := x
v := x
H2
v := f(z)
H1’
y := u
p(v)
1
v := x
v := f(z)
y := f(y)
u := f(u)
p(u)
0
0
p(z)
0
стоп(v,v)
z := f(v)
1
стоп(z,z)
p(u)
0
1
стоп(u,y)
u := f(u)
y := f(y)
z := f(v)
1
стоп(u,y)
Правда ли что u = v => вып замену термов (H1 экв
H2), удаляем неисольз. лин блоки (чёрные в цикле)
34.
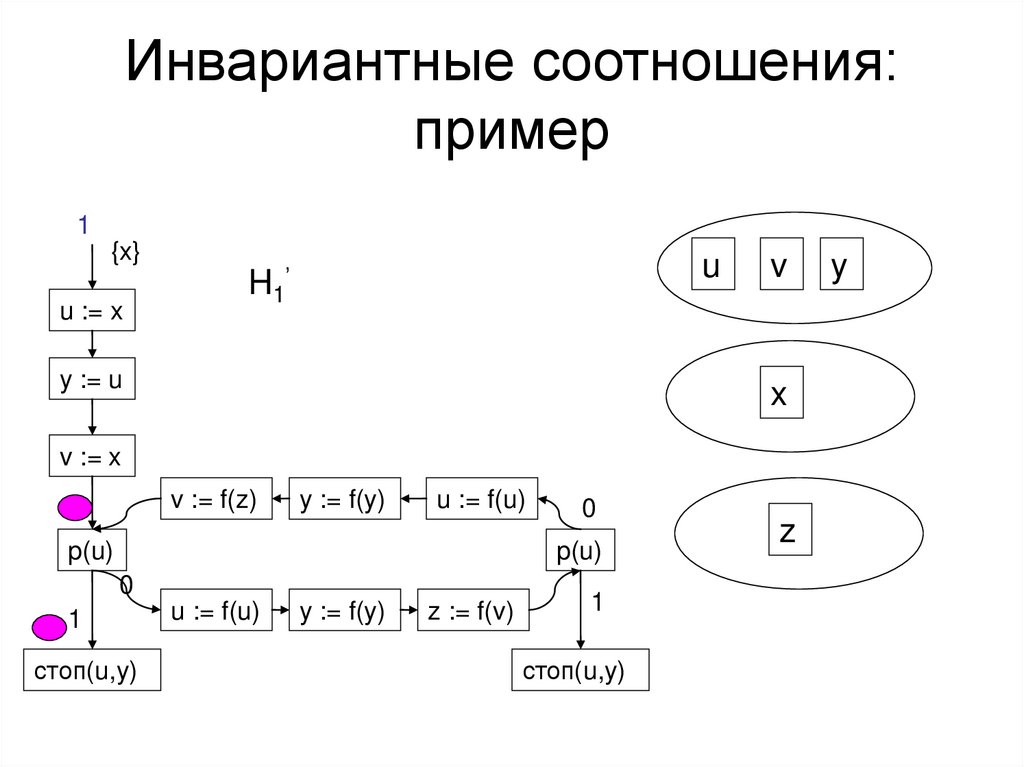
Доказательство теоремы• Найти инвариантные соотношения
перед каждым распознавателем,
выходом и остановом в H1.
• Если x – аргумент распознователя
(выхода, останова) в H1, а y –
соответствующий аргумент в H2, то
должно иметься соотношение x=y.
• Если нет, то фрагменты не лтэквивалентны.
35.
Инвариантные соотношения:пример
1
{x}
u := x
u
H1’
y := u
v
x
v := x
v := f(z)
y := f(y)
u := f(u)
p(u)
0
p(u)
0
1
стоп(u,y)
u := f(u)
y := f(y)
z := f(v)
1
стоп(u,y)
z
y
36.
Инвариантные соотношения:пример
1
{x}
u := x
H1’
y := u
v := x
v := f(z)
y := f(y)
u := f(u)
p(u)
0
p(u)
0
1
стоп(u,y)
u := f(u)
y := f(y)
z := f(v)
1
стоп(u,y)


























 Программирование
Программирование








