Логика предикатов. Машина Тьюринга. Лекция 3

1.

ЛЕКЦИЯ 3. ЛОГИКА
ПРЕДИКАТОВ. МАШИНА
ТЬЮРИНГА

2.

3.

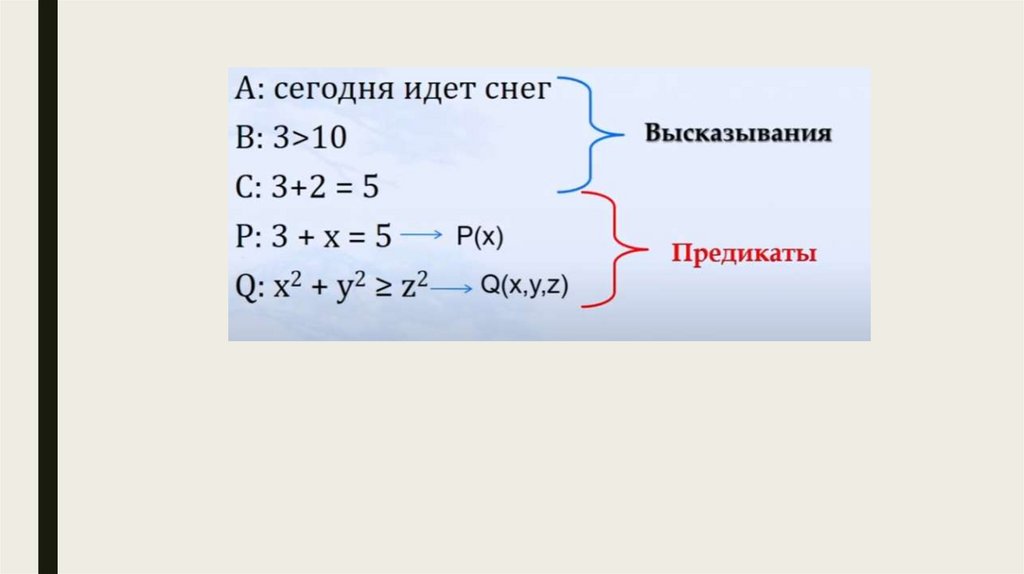
Предикаты
■ Предикатом (или высказывательной формой) называется
предложение с переменными, которое превращается в
высказывание при подстановке в него конкретных значений
переменных.
P(X): 3 + x = 5
P(2): 3 + 2 = 5
P(7): 3 + 7 = 5

4.

Предикаты
■ Одноместные – с одной переменной.
– P(n): n – простое число
■ Двуместные – с двумя переменными.
– P(x, y): x больше y
■ N-местные – с n переменных
– Q(x, y, z): 2*x + y = z/4

5.

Выполнимость предикатов
■ Предикат, заданный на множестве А1, А2, … ,Аn, называется:
■ Тождественно истинным, если при любой подстановке вместо переменных х1 ,
х2 , … , хn любых конкретных предметов а1 , а2 , …, аn из множеств А1, А2, … ,Аn
он превращается в истинное высказывание;
■ Тождественно ложным, если при любой подстановке вместо переменных х1, х2 ,
… , хn любых конкретных предметов а1 , а2 , …, аn из множеств А1 , А2 , … , Аn
он превращается в ложное высказывание;
■ Выполнимым (опровержимым), если существует по крайней мере один набор
предметов а1 , а2 , …, аn из множеств А1 , А2 , …, Аn, при подстановке которого
вместо соответствующих предметных переменных в предикат последний
превращается в истинное (ложное) высказывание

6.

■ P(x): x > 0, x ∈ N
■ P(x): x^2 = 3, x ∈ N
■ P(x, y): x + y = y^2, x ∈ N, y ∈ N

7.

Область определения и область
значения предиката
■ Совокупность всех допустимых значений переменной x называется областью
определения предиката. Обозначается Ua
■ Совокупность значений x, обеспечивающих истинность предиката, называется
множеством истинности предиката. Обозначается Ia.
■ Предикат С(х): «Движение разрешено, если горит х цвет светофора» одноместный предикат, выполнимый. Множество допустимых значений
■ Ua = «красный, желтый, зеленый»
■ Ia =«зеленый»

8.

Следствие предикатов
■ Предикат В(х) называют следствием предиката А(х), если множество истинности
предиката А(х) является частью множества истинности предиката В(х). Например,
из равенства х=0 следует, что sinx=0, но не наоборот
■ Предикаты А(х) и В(х) одной и той же областью определения равносильны тогда и
только тогда, когда В(х) есть следствие предиката А(х), и А(х) есть следствие
предиката В(х).

9.

Логические операции над
предикатами

10.

Пример логических операций
■ P(x): x – простое число, определен на множестве M: целых чисел и его областью
истинности являются простые числа (делятся на 1 и на себя)
■ !P(x): x – составное число
■ P(x): x – четное число, Q(x): x – делится на 7
■ P(x) • Q(x): - x четное число и делится на 7

11.

Кванторы
■ Квантор (quantum - сколько), логическая операция, дающая количественную
характеристику области предметов, к которой относится выражение, получаемое
в результате её применения
■ В математическую литературу кванторы вошли с середины 20 века. Их
используют для сокращения записей и превращение таких сокращенных
записей в удобный текст.
■ Кванторами называются символы ∀ и ∃, являющиеся сокращением:
■ ∀ – «для любого», «для каждого», «для всех»;
■ ∃ – «существует», «найдётся».

12.

Квантор всеобщности
■ Квантор всеобщности (универсальный квантор, квантор общности)
■ ∀x
■ Читается: «для всех…», «для каждого …», «для любого …» или «все»,
«каждый», «любой»
■ Истинно в том и только в том случае, когда предикат P(x),
тождественно истинен(выполняется для каждого значения
переменной x), и ложно в противном случае
■ ∀xS(x) – для любого x истинно S(x)

13.

Квантор всеобщности. Пример
■ P(x) – x грек
■ ∀xP(x) - все люди греки (ложное высказывание)
■ P(x): x^2 ≥ 0
■ ∀xP(x) – для любого x истинно x^2 ≥ 0 (истинное высказывание)

14.

Квантор существования
■ Квантор существования
■ ∃x
■ Читается: «существует…», «найдется …», «имеется
■ Истинно тогда и только тогда, когда для некоторых значениях x
выполняется предикат P(x)
■ ∃xP(x) – существует x такой, что P(x) истинно

15.

Квантор существования. Пример
■ P(x) – x грек
■ ∃xP(x) – существует человек, который является греком (истинное
высказывание)
■ P(x): x^2 = 4
■ ∃xP(x) – существует x, для которого выполняется x^2 =4 (истинное
высказывание)

16.

■ Кванторы часто применяются при записи математических теорем. Предикаты и
кванторы являются логической основой для построения экспертных систем
■ Помимо кванторов и вместе с ними часто используются символы «!», «:», «|»,
являющиеся сокращением:
■ ! – «единственный»;
■ : – «такой, что»;
■ | – «не такой, что».

17.

Применение кванторов к
естественному языку:

18.

Операции над кванторами.
■ Рассмотрим на множестве Х = {-2, -1, 0, 1, 2, 3, 4, 5, …,9} предикат А(х): «х –
натуральное число». Его отрицанием является предикат !(