Похожие презентации:
Корпускулярно - волновой дуализм
1.
ЭЛЕМЕНТЫ КВАНТОВОЙМЕХАНИКИ
2.
Корпускулярно-волновойдуализм
Фотоэффект, Комптон- эффект
электромагнитные волны- частицы –
корпускулы
Поляризация ,интерференция волны
3.
Свет – это волна иличастица?
С каждым объектом связаны
корпускулярные характеристики(E ,P)
и волновые (λ,ω)
E h
Формула де Бройля
h
P k
4.
ПримерДлина волны человека
m 60кг
V 1 м / с
h
6,63 10
P
60 1
34
1,1 10
Современными средствами не
измеряется
33
м
5.
Длина волны электрона, ускоренногоразностью потенциалов 100 В
mV
eU
2
2
2eU
V
m
19
2 1,6 10 100
6
5,93 10 м / с
31
9,1 10
34
h
6,63 10
10
м
31
6 1,23 10
P 9,1 10 5,93 10
6.
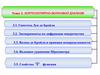
Опыт Дэвиссона и Джермера(1927)
П – электронная пушка
Э – приемник электронов
Рассеяние электронов наблюдается в
широком диапазоне углов и
удовлетворяет формуле ВульфаБрэггов
7.
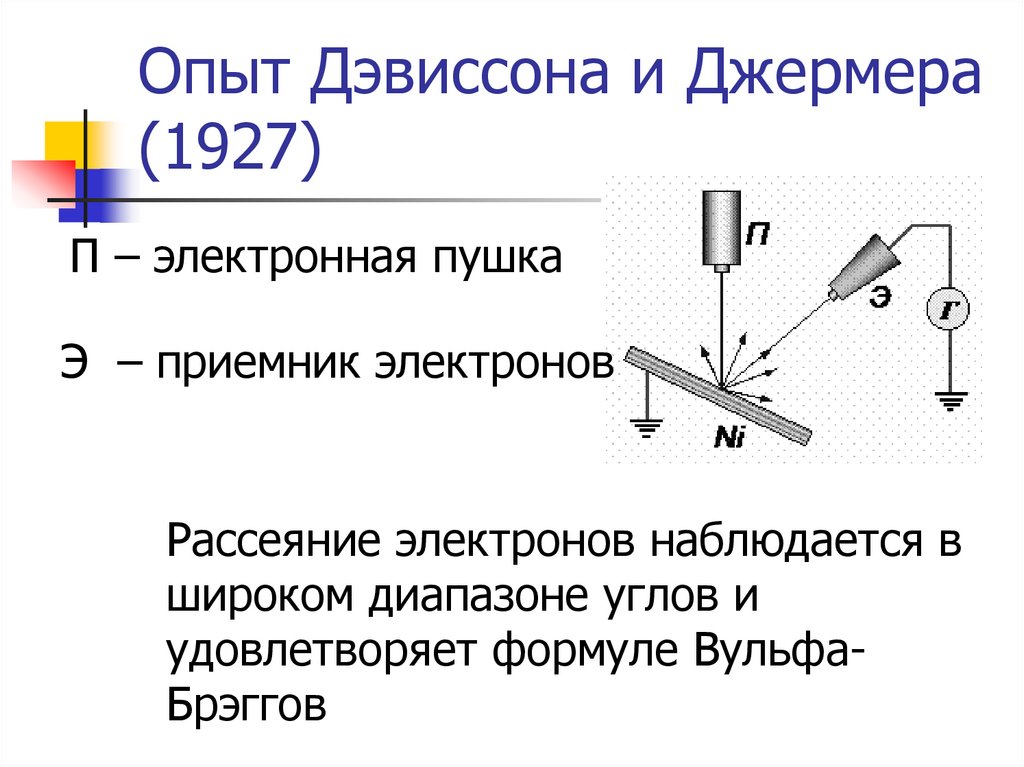
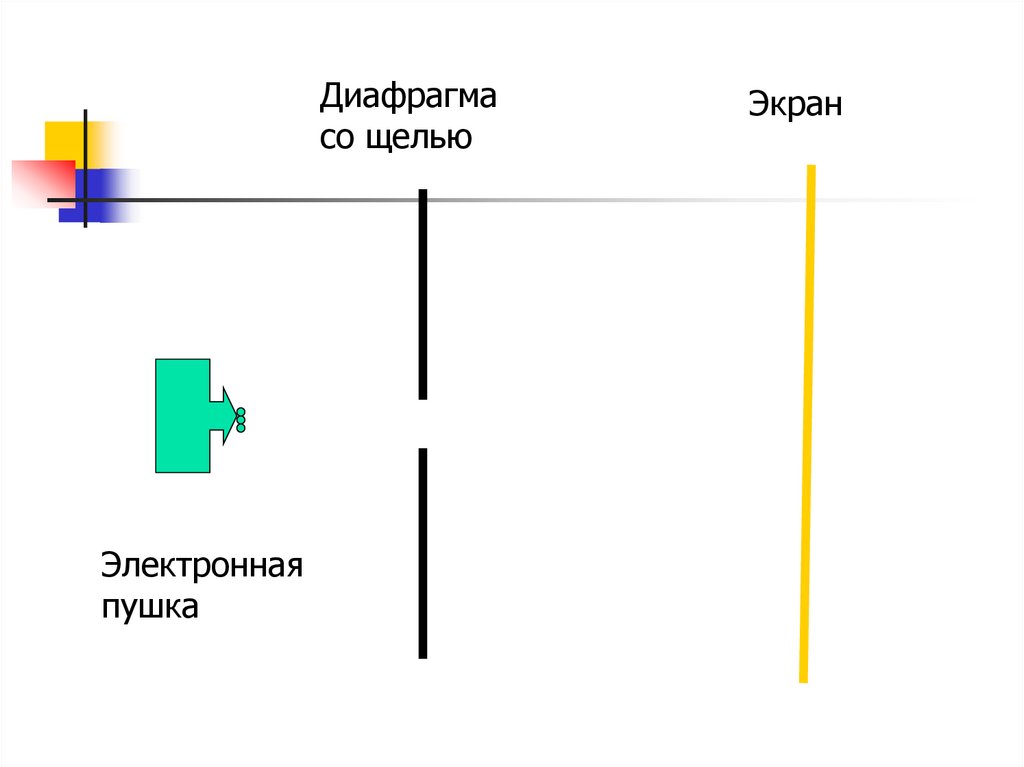
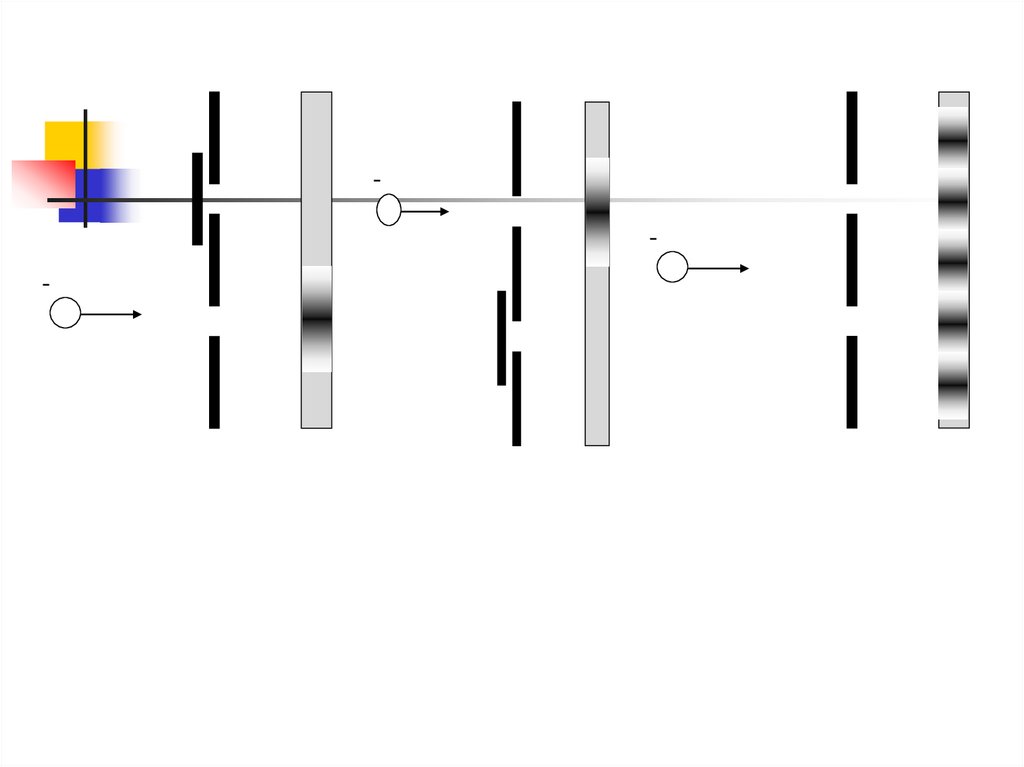
Опыт Фабриканта (1948)Электронная пушка стреляет по
одному электрону, а на экране
наблюдается дифракционная картина
8.
Диафрагмасо щелью
Электронная
пушка
Экран
9.
10.
Дифракционная картина11.
-12.
Соотношениенеопределенностей
1927 (Гейзенберг)
13.
В классической физике всегда точноможно сказать о координате частицы
и ее импульсе
14.
В квантовой физикеНевозможно одновременно точно
измерить координату и
соответствующую проекцию импульса
x p x h
15.
ПРИМЕР шарикm =1 г
Δх= 10-3м – точность
измерения координаты
неопределенность скорости
P
h
V
m
X m
34
6,63 10
28
3 3 6,63 10 м / с
10 10
16.
Электрон в атоменеопределенность скорости
V V
Для круговой орбиты радиуса
10
r 0,5 10
м
V 2,3 10 м/с
6
10
r 0,25 10
м
Сравнима с размерами атома и
понятие траектории теряет
физический смысл
17.
Соотношениенеопределенностей для
энергии и времени
E t
- ΔΕ – неопределенность измерения энергии
за данный промежуток времени Δt
18.
Размытие энергетических уровнейатомов (естественное уширение)
Время жизни атома в возбужденном
состоянии Δt =10-8 с
h
26
1.05 10 Дж
E
t
Е
7
1,58 10 Гц
h
Наблюдается в эксперименте
19.
ВОЛНОВАЯ ФУНКЦИЯ И ЕЕСТАТИСТИЧЕСКИЙ СМЫСЛ
В квантовой механике состояние
частицы задается комплексной
величиной
( x, y , z , t )
- Волновая функция
20.
Физический смысл имеет плотностьвероятности – вероятность
нахождения частицы в единице
объема
W
*
2
- квадрат модуля волновой функции
Вероятность нахождения частицы в
объеме dV
dW dV
2
21.
Условие нормировки2
dV
1
Вероятность нахождения
частицы во всем
пространстве =1 , где-то
частица есть
22.
Принцип суперпозицииЕсли у некоторой системы возможными
являются состояния с 1 и 2 ,
то также возможно состояние
c1 1 c2 2
23.
Уравнение ШредингераВвести уравнение ( аналогичное
закону Ньютона), которому бы
удовлетворяла волновая функция
U i
2m
t
2
m- масса частицы
U- потенциальная энергия
24.
Оператор Лапласа2 ( x, y, z, t ) 2 ( x, y, z, t ) 2 ( x, y, z, t )
2
2
2
x
y
z
25.
Основная задача квантовой механикинайти вид волновой функции для
каждой конкретной задачи
26.
Волновая функцияКонечная, однозначная, непрерывная
Ее производные должны быть
конечны, однозначны, непрерывны
2
*
интегрируемая
27.
Решения уравнения Шредингеравозможны только для некоторых
дискретных значений энергии Е
Квантование энергии
Собственные значения энергии
28.
Уравнение Шредингера длястационарных состояний
Если силовое поле не меняется с
течением времени (поле
стационарно)
U U ( x, y , z )
( x, y, z, t ) ( x, y, z )e
E
i t
29.
( x, y, z, t ) ( x, y, z, t )2
*
( x, y, z ) ( x, y, z )e
*
i t i t
( x, y, z ) ( x, y, z )
*
*
e
30.
Подставим в уравнениеШредингера
U i
2m
t
2
( x, y, z )e
i t
i ( x, y, z )e
t
i t
31.
22m
ψ e iωt Uψ e iωt i ( iω)e iωt ψ
E
2
2m
ψ Uψ Eψ
32.
22m
ψ E U ψ 0
Уравнение Шредингера для
стационарных состояний
33.
Движение свободнойчастицы
U ( x, y , z ) 0
2
U E 0
2m
2
E 0
2m
34.
Рассмотрим одномерный случайAe
ikx
d
d
ikx
2 Ae ik
dx
dx
2
Ae (ik )
ikx
2
k
2
35.
2k
E 0
2m
2 2
2 Px
k
k
E
2m
2
Px – может принимать любые значения
2
P
E
2m
– может принимать любые значения,
энергетический спектр непрерывный
36.
Найдем плотность вероятностиобнаружения частицы в некоторой
точке пространства
( x, t ) ( x)e
i ( t kx )
Ae
i t
ikx i t
Ae e
i ( t kx )
* ( x, t ) Ae
i ( t kx )
i ( t kx )
2
* Ae
Ae
A
вероятность обнаружения свободной частицы
не зависит от ее положения в пространстве
и везде одинакова























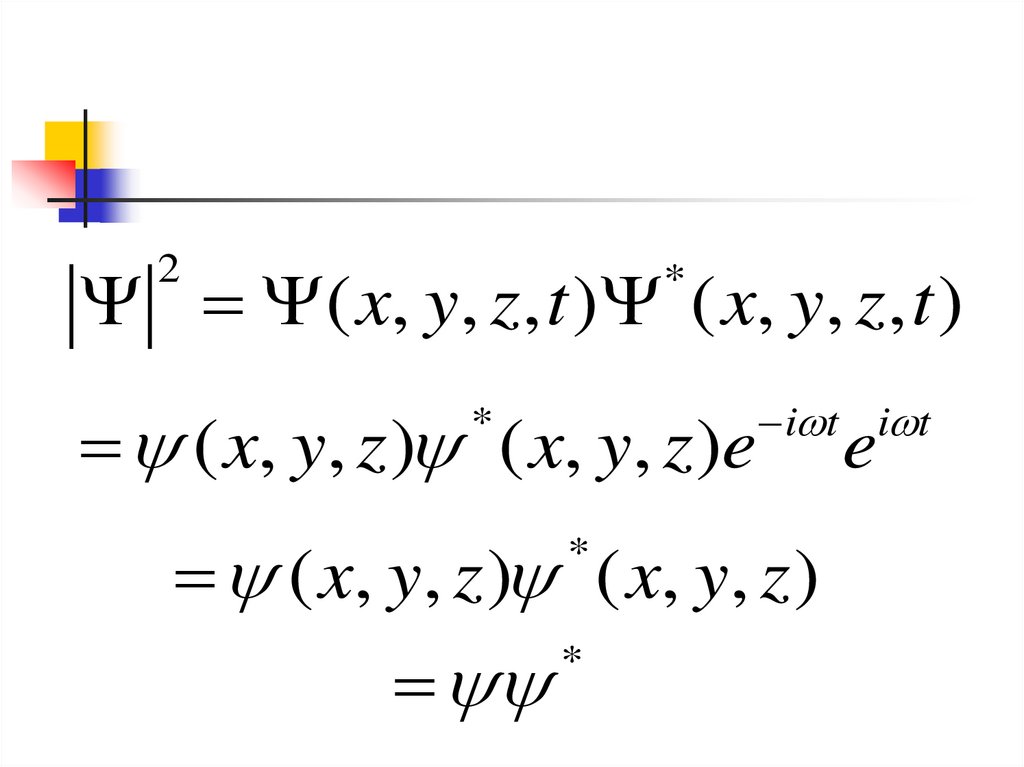

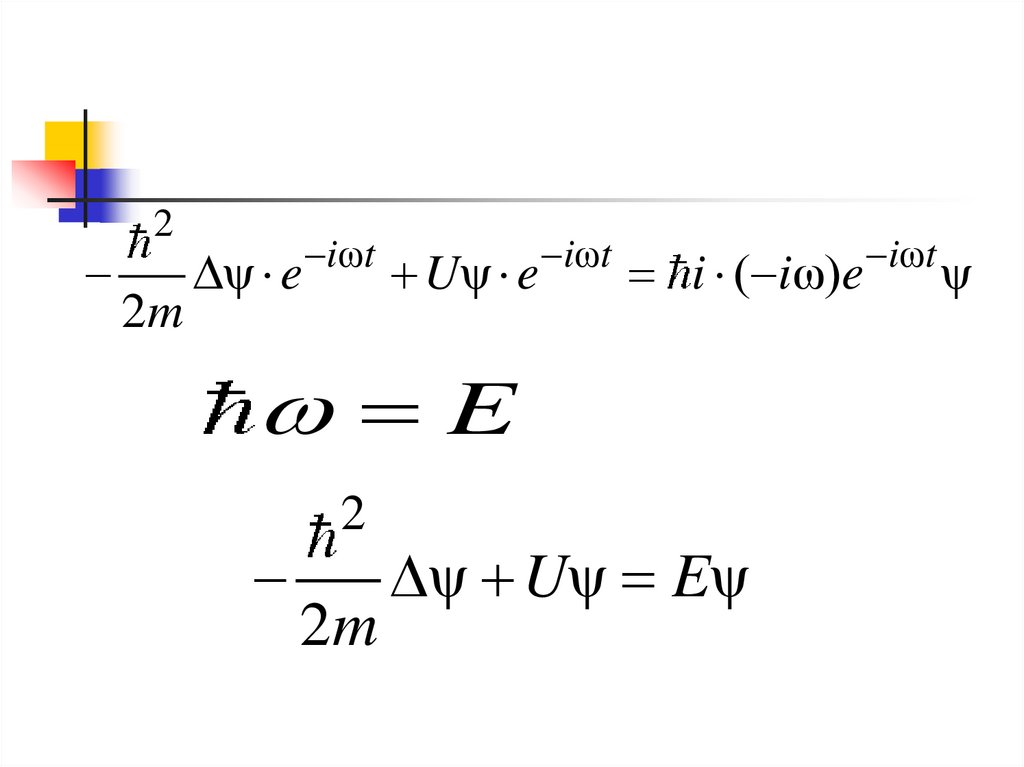





 Физика
Физика