Міріадний ЛАФ

1. Лекція 10 Міріадний ЛАФ

Деякі властивості звичайного міріадного фільтра
Оптимальне (квазіоптимальне) значення параметра k для фрагмента сигналу
(у сенсі забезпечення мінімальної локальної СКО) і залежить від масштабу
даних для розглянутого фрагмента.
Масштаб для заданого положення ковзного вікна одночасно визначається
характеристиками завад і сигналу:
- для сигналу постійного рівня масштаб даних у ковзному вікні визначається
середньоквадратичним відхиленням завад;
- для лінійно-змінного сигналу масштаб даних насамперед залежить від ∆S;
- для околу різкого перепаду міріадний фільтр при малому k здатний
забезпечити кращу обробку сигналу, ніж стандартний медіанний фільтр –
ця властивість рідко відзначається в літературі і вона невідома більшості
дослідників.
National Aerospace University
1

2. Лекція 10 Міріадний ЛАФ

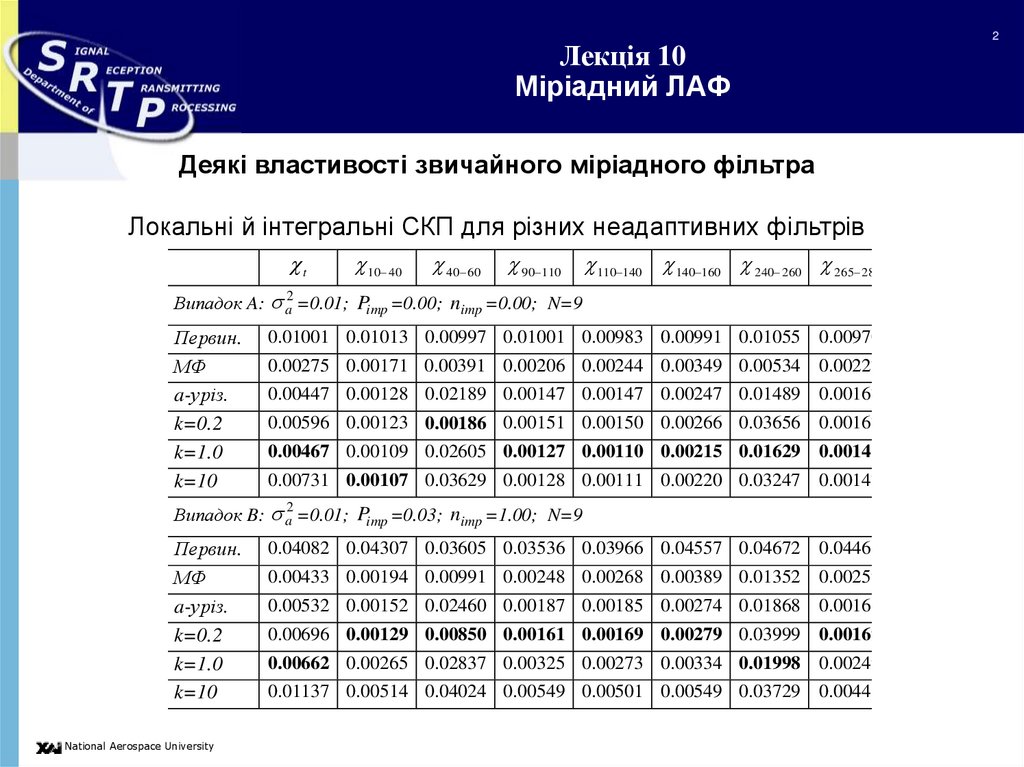
Деякі властивості звичайного міріадного фільтра
Локальні й інтегральні СКП для різних неадаптивних фільтрів
t
10 40
40 60
90 110
110 140 140 160 240 260 265 285
Випадок A: a2 =0.01; Pimp =0.00; nimp =0.00; N=9
Первин.
МФ
a-уріз.
k=0.2
k=1.0
k=10
0.01001 0.01013 0.00997 0.01001 0.00983 0.00991 0.01055 0.00970
0.00275 0.00171 0.00391 0.00206 0.00244 0.00349 0.00534 0.00227
0.00447 0.00128 0.02189 0.00147 0.00147 0.00247 0.01489 0.00167
0.00596 0.00123 0.00186 0.00151 0.00150 0.00266 0.03656 0.00167
0.00467 0.00109 0.02605 0.00127 0.00110 0.00215 0.01629 0.00141
0.00731 0.00107 0.03629 0.00128 0.00111 0.00220 0.03247 0.00147
Випадок B: a =0.01; Pimp =0.03; nimp =1.00; N=9
2
Первин.
МФ
a-уріз.
k=0.2
k=1.0
k=10
National Aerospace University
0.04082 0.04307 0.03605 0.03536 0.03966 0.04557 0.04672 0.04468
0.00433 0.00194 0.00991 0.00248 0.00268 0.00389 0.01352 0.00259
0.00532 0.00152 0.02460 0.00187 0.00185 0.00274 0.01868 0.00165
0.00696 0.00129 0.00850 0.00161 0.00169 0.00279 0.03999 0.00169
0.00662 0.00265 0.02837 0.00325 0.00273 0.00334 0.01998 0.00249
0.01137 0.00514 0.04024 0.00549 0.00501 0.00549 0.03729 0.00446
2

3. Лекція 10 Міріадний ЛАФ

Передумови розробки адаптивного міріадного фільтра (АМФ)
1) Звичайний міріадний фільтр (ЗМФ) при оптимальному значенні k часто
забезпечує менші локальні СКО, ніж традиційні неадаптивні фільтри (МФ і
α-урізаний).
2) ЗМФ при відносно малих k має дуже хорошу стійкість до імпульсних завад.
3) Змінюючи параметр k, можна забезпечувати мінімальні (або прийнятно
малі) локальні СКП для різних фрагментів оброблюваного сигналу.
4) Шляхом мінімізації локальних СКП можна мінімізувати СКП всього
сигналу.
5) Параметр k можна адаптивним чином змінювати з урахуванням локальної
поведінки сигналу та властивостей перешкод (їх локального масштабу) чим більше "масштаб", тим більше має бути значення k.
6) Адаптивний вибір k має бути стійким до можливої присутності імпульсних
заад.
Для різкого перепаду потрібно використовувати відносно малі значення k для
того, щоб зберегти його.
National Aerospace University
3

4. Лекція 10 Міріадний ЛАФ

Узагальнений принцип розробки адаптивного міріадного фільтра
Основна ідея - для кожного положення ковзного вікна розрахувати деякий
ПЛА і далі отримати поточне значення параметра k (що адаптується до
локальних властивостей сигналу та завад) у вигляді
Найпростіший варіант - лінійна залежність виду
Якщо такий варіант виявиться працездатним, то виникає наступне питання –
яким є оптимальний коефіцієнт пропорційності.
National Aerospace University
4

5. Лекція 10 Міріадний ЛАФ

Можливі варіанти розрахунку
Квазірізмах – АМФ AdaptI
QRipq xi q xi p ,
дде xi r - r-я порядкова статистика виборки данихх xi розміру N,
що сформована із значень в околі i-го відліку.
Квазірозмах, оброблений МФ – фільтр AdaptII
MdQRipq med QR jpq ,
де j i N 2 , i N 2 .
National Aerospace University
5

6. Лекція 10 Міріадний ЛАФ

Можливі варіанти розрахунку
Абсолютне медіанне відхилення – фільтр AdaptIII
MADi med x j med xi .
“Мінімізований” квазірозмах – фільтр Adapt IV
l
MQRim min Qlm ,
де l m 1, N m ; Qlm xi l m xi l m .
National Aerospace University
6

7. Лекція 10 Міріадний ЛАФ

7
Лекція 10
Міріадний ЛАФ
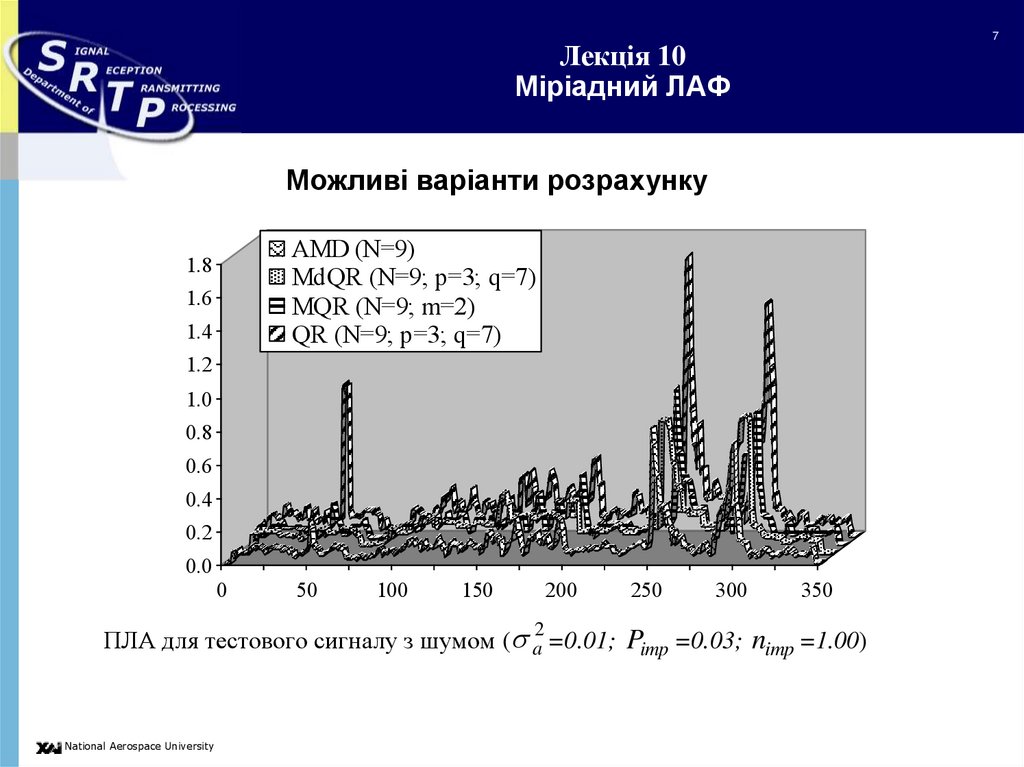
Можливі варіанти розрахунку
AMD (N=9)
MdQR (N=9; p=3; q=7)
MQR (N=9; m=2)
QR (N=9; p=3; q=7)
1.8
1.6
1.4
1.2
1.0
0.8
0.6
0.4
0.2
0.0
0
50
100
200
150
250
300
350
ПЛА для тестового сигналу з шумом ( a =0.01; Pimp =0.03; nimp =1.00)
2
National Aerospace University

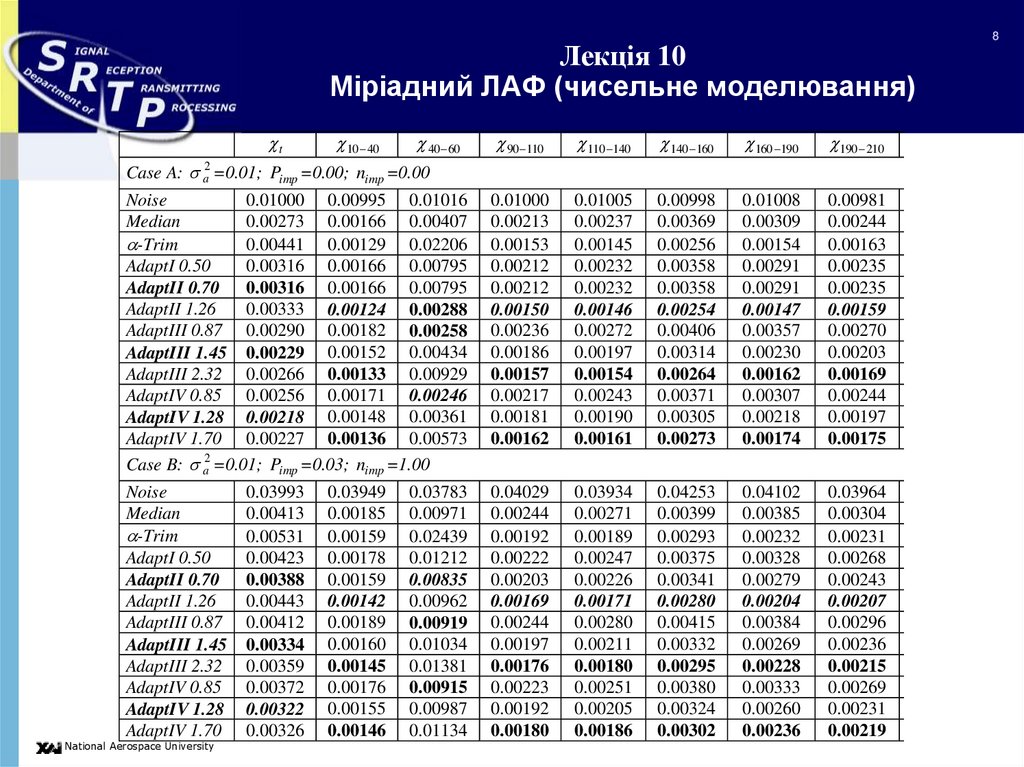
8. Лекція 10 Міріадний ЛАФ (чисельне моделювання)

8
90 110
110 140
140 160
160 190
190 210
240 260
265
Noise
0.01000 0.00995 0.01016
Median
0.00273 0.00166 0.00407
-Trim
0.00441 0.00129 0.02206
AdaptI 0.50
0.00316 0.00166 0.00795
AdaptII 0.70 0.00316 0.00166 0.00795
AdaptII 1.26
0.00333 0.00124 0.00288
AdaptIII 0.87 0.00290 0.00182 0.00258
AdaptIII 1.45 0.00229 0.00152 0.00434
AdaptIII 2.32 0.00266 0.00133 0.00929
AdaptIV 0.85 0.00256 0.00171 0.00246
AdaptIV 1.28 0.00218 0.00148 0.00361
AdaptIV 1.70 0.00227 0.00136 0.00573
Case B: a2 =0.01; Pimp =0.03; nimp =1.00
0.01000
0.00213
0.00153
0.00212
0.00212
0.00150
0.00236
0.00186
0.00157
0.00217
0.00181
0.00162
0.01005
0.00237
0.00145
0.00232
0.00232
0.00146
0.00272
0.00197
0.00154
0.00243
0.00190
0.00161
0.00998
0.00369
0.00256
0.00358
0.00358
0.00254
0.00406
0.00314
0.00264
0.00371
0.00305
0.00273
0.01008
0.00309
0.00154
0.00291
0.00291
0.00147
0.00357
0.00230
0.00162
0.00307
0.00218
0.00174
0.00981
0.00244
0.00163
0.00235
0.00235
0.00159
0.00270
0.00203
0.00169
0.00244
0.00197
0.00175
0.00991
0.00542
0.01485
0.00723
0.00723
0.01581
0.00581
0.00392
0.00657
0.00462
0.00374
0.00483
0.01
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
Noise
Median
-Trim
AdaptI 0.50
AdaptII 0.70
AdaptII 1.26
AdaptIII 0.87
AdaptIII 1.45
AdaptIII 2.32
AdaptIV 0.85
AdaptIV 1.28
AdaptIV 1.70
0.04029
0.00244
0.00192
0.00222
0.00203
0.00169
0.00244
0.00197
0.00176
0.00223
0.00192
0.00180
0.03934
0.00271
0.00189
0.00247
0.00226
0.00171
0.00280
0.00211
0.00180
0.00251
0.00205
0.00186
0.04253
0.00399
0.00293
0.00375
0.00341
0.00280
0.00415
0.00332
0.00295
0.00380
0.00324
0.00302
0.04102
0.00385
0.00232
0.00328
0.00279
0.00204
0.00384
0.00269
0.00228
0.00333
0.00260
0.00236
0.03964
0.00304
0.00231
0.00268
0.00243
0.00207
0.00296
0.00236
0.00215
0.00269
0.00231
0.00219
0.04015
0.01232
0.01846
0.01310
0.01373
0.01989
0.01200
0.00873
0.01068
0.01043
0.00838
0.00899
0.04
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
t
10 40
40 60
Case A: a2 =0.01; Pimp =0.00; nimp =0.00
National Aerospace University
0.03993
0.00413
0.00531
0.00423
0.00388
0.00443
0.00412
0.00334
0.00359
0.00372
0.00322
0.00326
0.03949
0.00185
0.00159
0.00178
0.00159
0.00142
0.00189
0.00160
0.00145
0.00176
0.00155
0.00146
0.03783
0.00971
0.02439
0.01212
0.00835
0.00962
0.00919
0.01034
0.01381
0.00915
0.00987
0.01134

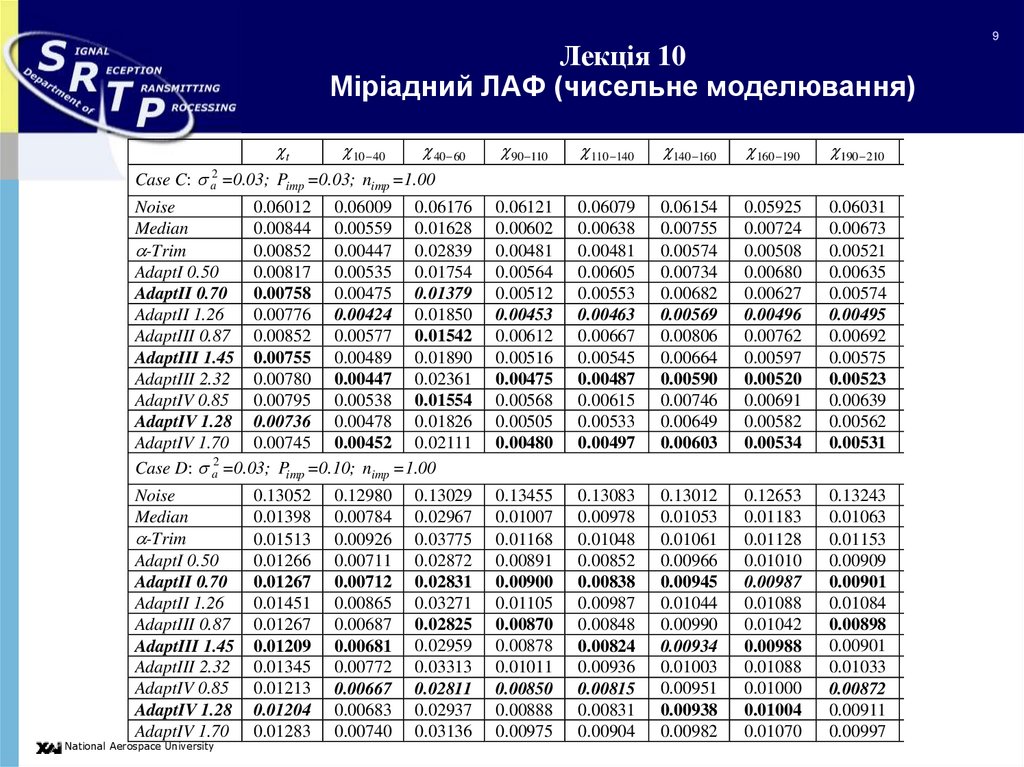
9. Лекція 10 Міріадний ЛАФ (чисельне моделювання)

9
90 110
110 140
140 160
160 190
190 210
240 260
265
Noise
0.06012 0.06009 0.06176
Median
0.00844 0.00559 0.01628
-Trim
0.00852 0.00447 0.02839
AdaptI 0.50
0.00817 0.00535 0.01754
AdaptII 0.70 0.00758 0.00475 0.01379
AdaptII 1.26
0.00776 0.00424 0.01850
AdaptIII 0.87 0.00852 0.00577 0.01542
AdaptIII 1.45 0.00755 0.00489 0.01890
AdaptIII 2.32 0.00780 0.00447 0.02361
AdaptIV 0.85 0.00795 0.00538 0.01554
AdaptIV 1.28 0.00736 0.00478 0.01826
AdaptIV 1.70 0.00745 0.00452 0.02111
Case D: a2 =0.03; Pimp =0.10; nimp =1.00
0.06121
0.00602
0.00481
0.00564
0.00512
0.00453
0.00612
0.00516
0.00475
0.00568
0.00505
0.00480
0.06079
0.00638
0.00481
0.00605
0.00553
0.00463
0.00667
0.00545
0.00487
0.00615
0.00533
0.00497
0.06154
0.00755
0.00574
0.00734
0.00682
0.00569
0.00806
0.00664
0.00590
0.00746
0.00649
0.00603
0.05925
0.00724
0.00508
0.00680
0.00627
0.00496
0.00762
0.00597
0.00520
0.00691
0.00582
0.00534
0.06031
0.00673
0.00521
0.00635
0.00574
0.00495
0.00692
0.00575
0.00523
0.00639
0.00562
0.00531
0.05879
0.01945
0.02332
0.01854
0.01947
0.02346
0.01893
0.01655
0.01974
0.01729
0.01608
0.01760
0.05
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
Noise
Median
-Trim
AdaptI 0.50
AdaptII 0.70
AdaptII 1.26
AdaptIII 0.87
AdaptIII 1.45
AdaptIII 2.32
AdaptIV 0.85
AdaptIV 1.28
AdaptIV 1.70
0.13455
0.01007
0.01168
0.00891
0.00900
0.01105
0.00870
0.00878
0.01011
0.00850
0.00888
0.00975
0.13083
0.00978
0.01048
0.00852
0.00838
0.00987
0.00848
0.00824
0.00936
0.00815
0.00831
0.00904
0.13012
0.01053
0.01061
0.00966
0.00945
0.01044
0.00990
0.00934
0.01003
0.00951
0.00938
0.00982
0.12653
0.01183
0.01128
0.01010
0.00987
0.01088
0.01042
0.00988
0.01088
0.01000
0.01004
0.01070
0.13243
0.01063
0.01153
0.00909
0.00901
0.01084
0.00898
0.00901
0.01033
0.00872
0.00911
0.00997
0.12454
0.03580
0.03551
0.03274
0.03376
0.03665
0.03345
0.02964
0.03226
0.03101
0.02888
0.03004
0.12
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
t
10 40
40 60
Case C: a2 =0.03; Pimp =0.03; nimp =1.00
National Aerospace University
0.13052
0.01398
0.01513
0.01266
0.01267
0.01451
0.01267
0.01209
0.01345
0.01213
0.01204
0.01283
0.12980
0.00784
0.00926
0.00711
0.00712
0.00865
0.00687
0.00681
0.00772
0.00667
0.00683
0.00740
0.13029
0.02967
0.03775
0.02872
0.02831
0.03271
0.02825
0.02959
0.03313
0.02811
0.02937
0.03136

10. Лекція 10 Міріадний ЛАФ

10
Лекція 10
Міріадний ЛАФ
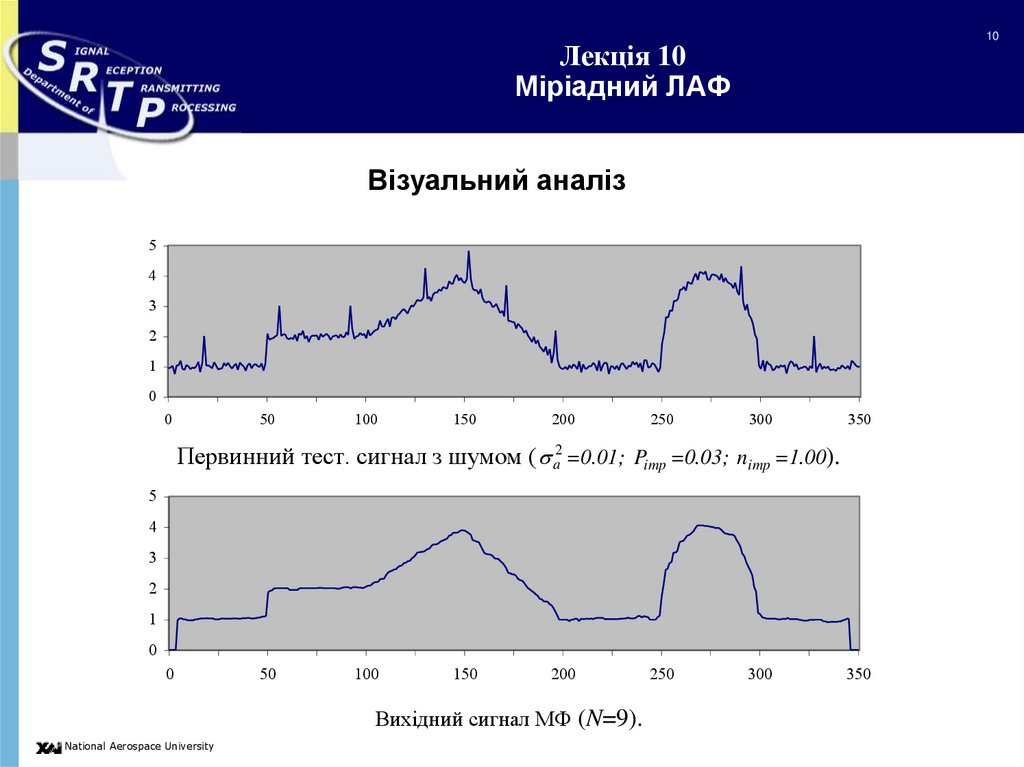
Візуальний аналіз
5
4
3
2
1
0
0
50
100
150
200
250
300
350
Первинний тест. сигнал з шумом ( a2 =0.01; Pimp =0.03; nimp =1.00).
5
4
3
2
1
0
0
50
100
150
200
Вихідний сигнал МФ (N=9).
National Aerospace University
250
300
350

11. Лекція 10 Міріадний ЛАФ

11
Лекція 10
Міріадний ЛАФ
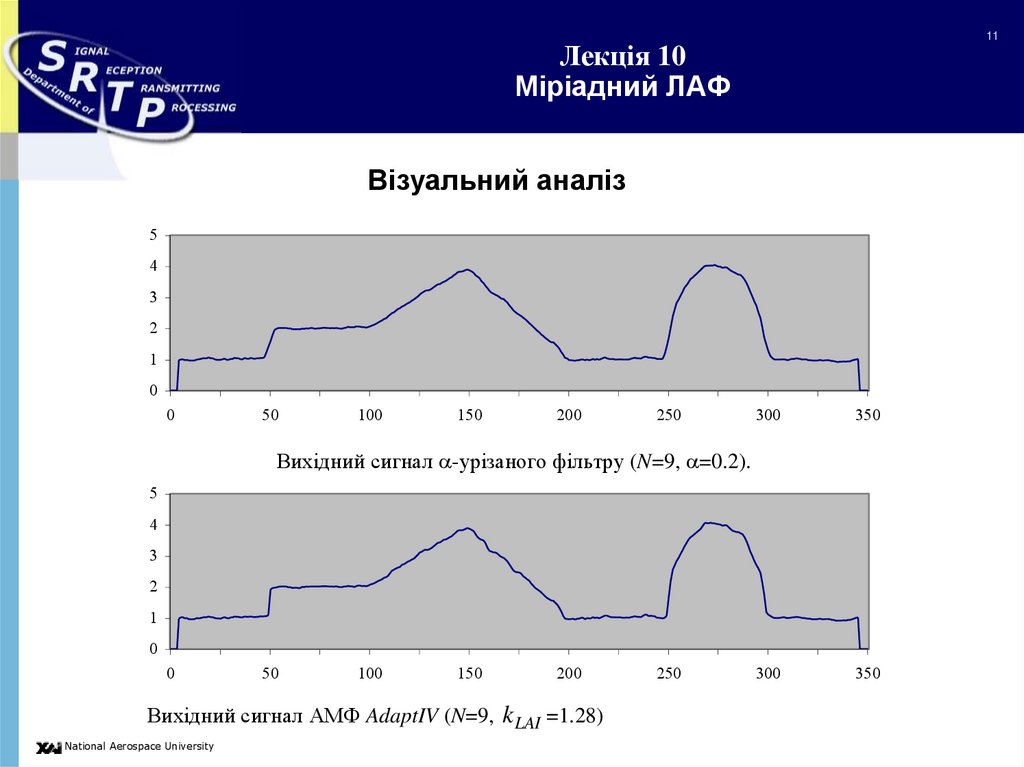
Візуальний аналіз
5
4
3
2
1
0
0
50
100
150
200
250
300
350
300
350
Вихідний сигнал -урізаного фільтру (N=9, =0.2).
5
4
3
2
1
0
0
50
100
150
200
Вихідний сигнал АМФ AdaptIV (N=9, k LAI =1.28)
National Aerospace University
250

12. Лекція 10 Міріадний ЛАФ

12
Властивості та переваги АМФ
1. Розроблені АМФ, особливо АМФ на основі ПЛА типу АМО і мінімізований
квазірозмах володіють прийнятним компромісом властивостей у плані
придушення завад, стійкості та збереження інформативних фрагментів.
2. Для розглянутого тестового сигналу та завадових ситуацій вони
забезпечують покращення ССШ на 7...11 дБ. По СКП для всього сигналу ці
АМФ забезпечують виграш у порівнянні з МФ і α-урізаним фільтром з тими ж
розмірами ковзного вікна.
3. Важливо також, що ці АМФ забезпечують краще збереження різкого перепаду
ніж МФ, який за цією властивістю зазвичай вважають найкращим серед
нелінійних фільтрів.
4. За рахунок вибору k можна дещо варіювати властивості розроблених АМФ.
Збільшення k призводить до поліпшення ступеня придушення флуктуаційних
перешкод за рахунок деякого погіршення здатності зберігати перепади та
усувати імпульсні завади.
5. Перевагою АМФ основі ПЛА типу АМО та мінімізований квазірозмах у
порівнянні з ЛАФ на основі Z-параметрів є менша затримка отримання
вихідного сигналу.
National Aerospace University