Похожие презентации:
Дискретная математика. Лекция 1. Множества
1.
Дискретная математикаЛекция 1
Множества
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
Бином Ньютона55.
56.
57.
58.
59.
60.
61.
ЗАДАЧИЗадача 1
В учебной группе N = 20 студентов. Для выполнения
проективного задания из них нужно отобрать группу из K = 8
человек. Сколько различных групп можно создать?
62.
Решение63.
ЗАДАЧИЗадача 2
Сколько различных слов, состоящих из K = 8 букв можно
составить из алфавита, в котором 30 букв? Считать словом
любую комбинацию букв, независимо от смысла.
64.
Решение65.
ЗАДАЧИЗадача 3
В поезде 18 вагонов. Сколькими способами можно рассадить
N = 10 человек, если они должны ехать в разных вагонах?
66.
РешениеТак как пассажиры должны ехать в различных вагонах, требуется
отобрать 10 вагонов из 18 с учетом порядка (вагоны могут отличаться
номерами), эти выборки – размещения из n = 18 различных элементов по m
= 10 элементов. Число таких размещений находим по формуле:
67.
ЗАДАЧИЗадача 4
Сколькими способами можно рассадить за столом K = 8
гостей на К = 8 стульев
68.
Решение69.
ЗАДАЧИЗадача 5
В буфете продаются пирожки с начинкой K = 8 видов.
Сколькими способами можно купить N = 10 пирожков.
70.
РешениеДанная
задача
на
отыскание
повторениями из 8 элементов по 10
числа
сочетаний
с
71.
ЗАДАЧИЗадача 6
Сколько различных буквосочетаний можно получить
перестановкой букв в Вашем имени?
Имя: ИРИНА
72.
РешениеКоличество букв n = 5
Количество возможных перестановок:
Однако, в имени "ИРИНА" есть две буквы И, а при
перестановке их местами не меняется смысл слова, поэтому
результат нужно поделить на 2. То есть 5! / 2 = 120 / 2 = 60
различных вариантов.




















































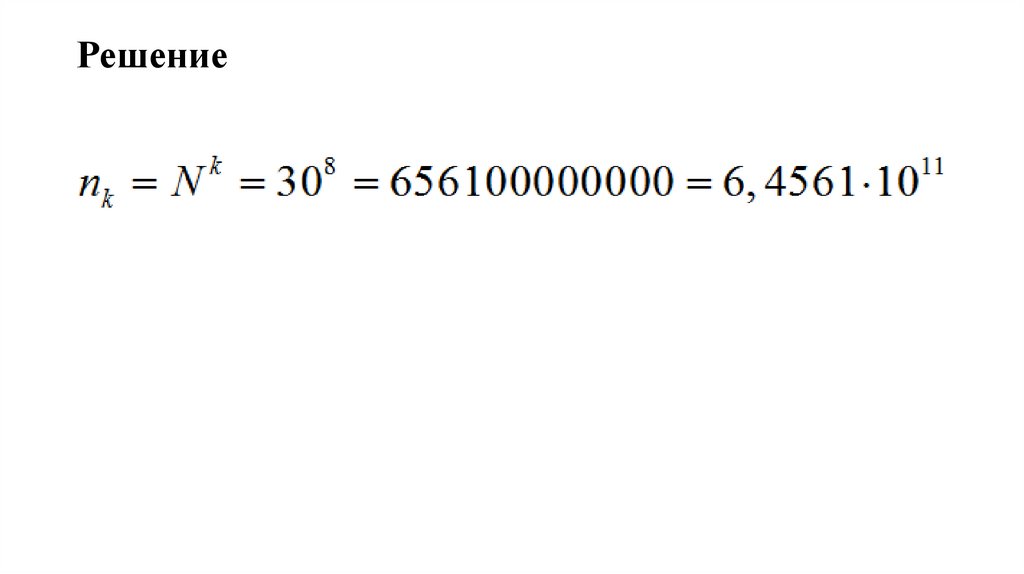



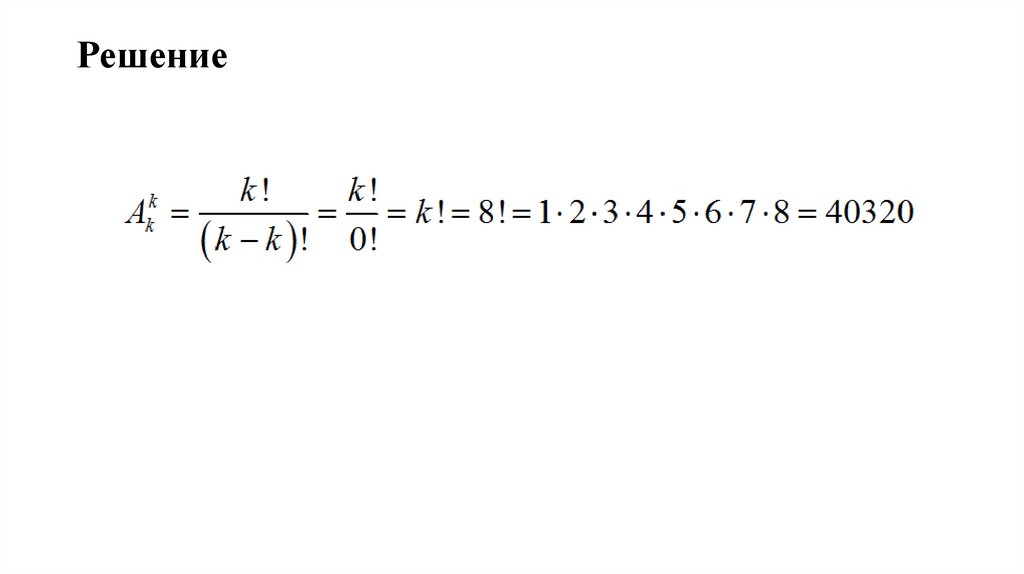





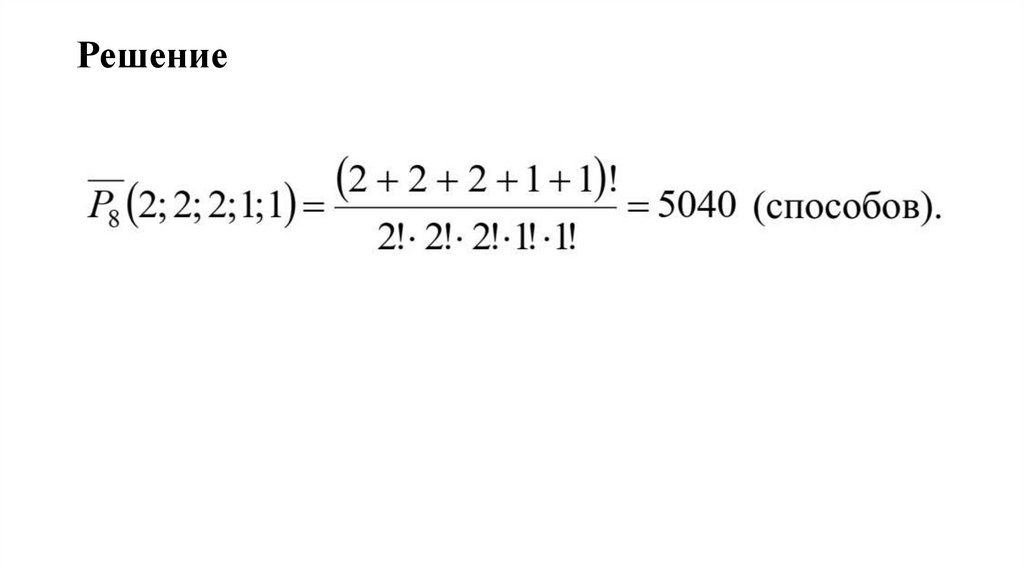

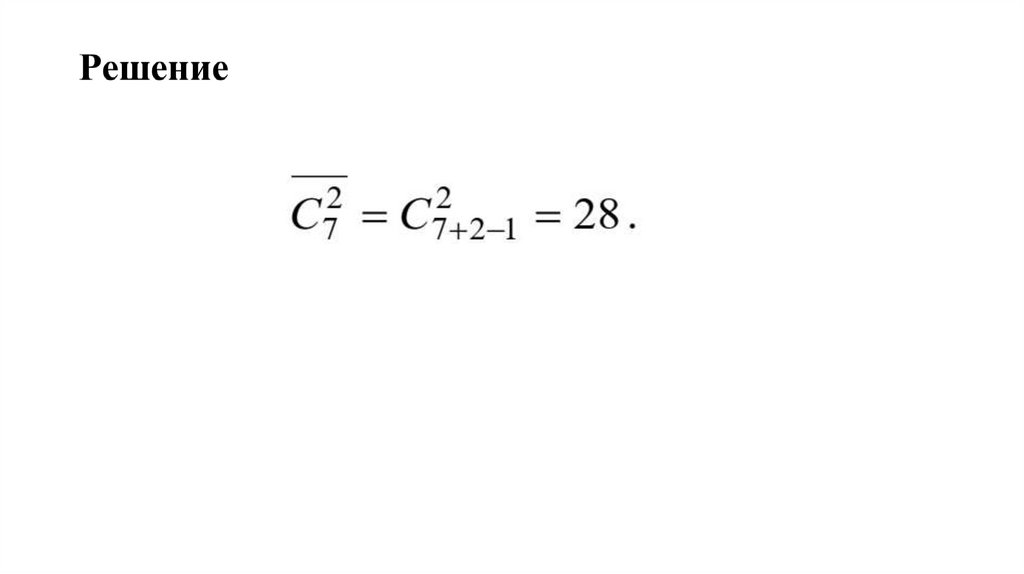
 Математика
Математика








