Геометрия. Задание №24

1.

Основной государственный экзамен

2.

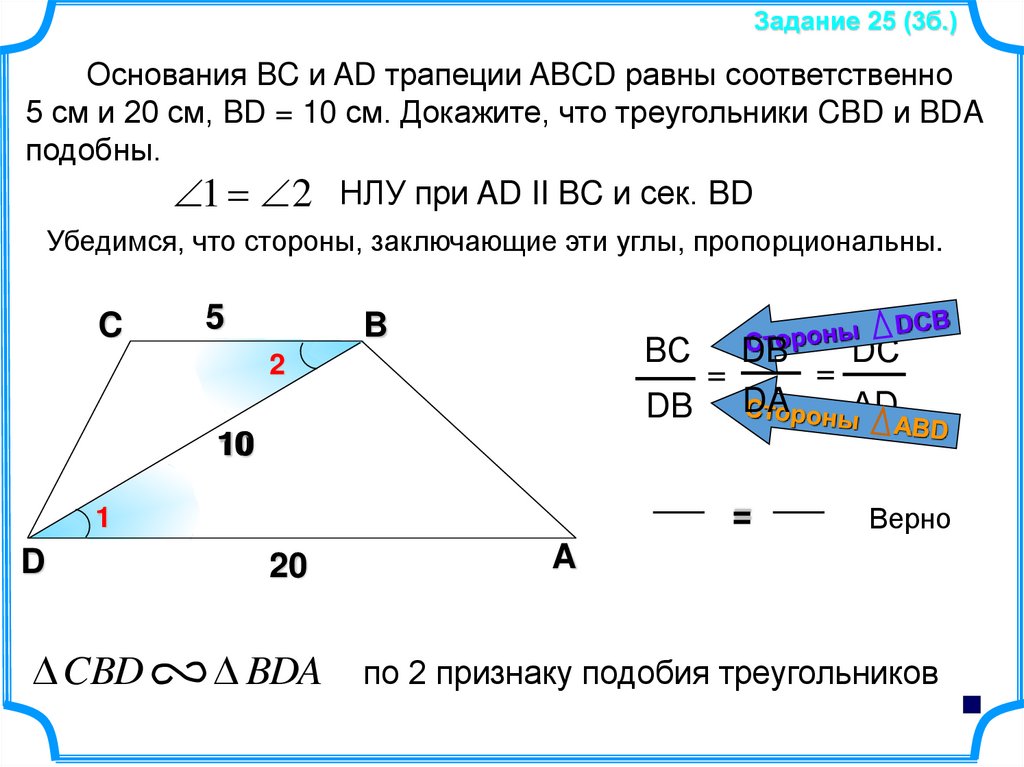
Задание 25 (3б.)
Основания BC и AD трапеции ABCD равны соответственно
5 см и 20 см, BD = 10 см. Докажите, что треугольники CBD и BDA
подобны.
1 2 НЛУ при AD II BC и сек. BD
Убедимся, что стороны, заключающие эти углы, пропорциональны.
C
5
B
BС
DB
DС
=
=
АD
DB DA
2
10
=
1
D
CBD
20
Верно
A
BDA по 2 признаку подобия треугольников

3.

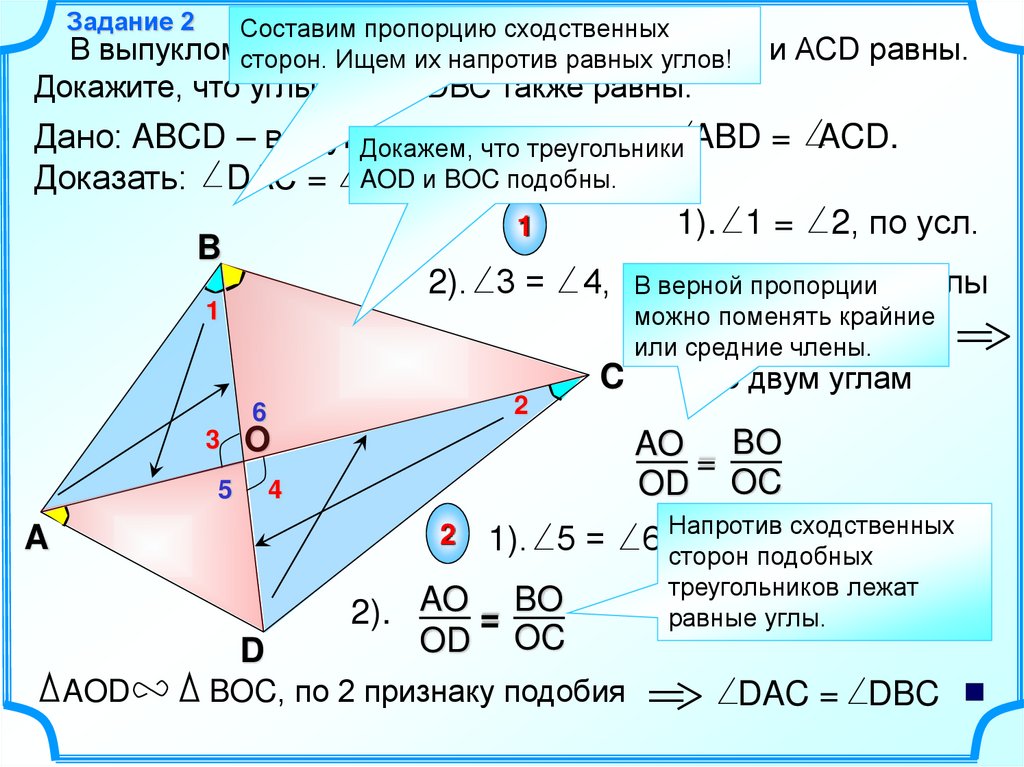
Задание 2
Составим пропорцию сходственных
В выпукломсторон.
четырехугольнике
АВСD
углы
АВD и АСD равны.
Ищем их напротив
равных
углов!
Докажите, что углы DАС и DВС также равны.
Дано: ABCD – выпук.Докажем,
четырехугольник,
что треугольники ABD = ACD.
и BOC подобны.
Доказать: DАС = AOD
DBC.
1). 1 = 2, по усл.
1
B
2). 3 = 4, как
вертикальные
В верной
пропорции углы
1
можно поменять крайние
ABO члены.
DCO,
или средние
C
2
6
3
O
5
4
AO BO
=
OD OC
2
A
D
AOD
по двум углам
1). 5 =
2). AO = BO
OD OC
BOC, по 2 признаку подобия
сходственных
6,Напротив
вертикальные
углы
сторон подобных
треугольников лежат
равные углы.
DAC = DBC

4.

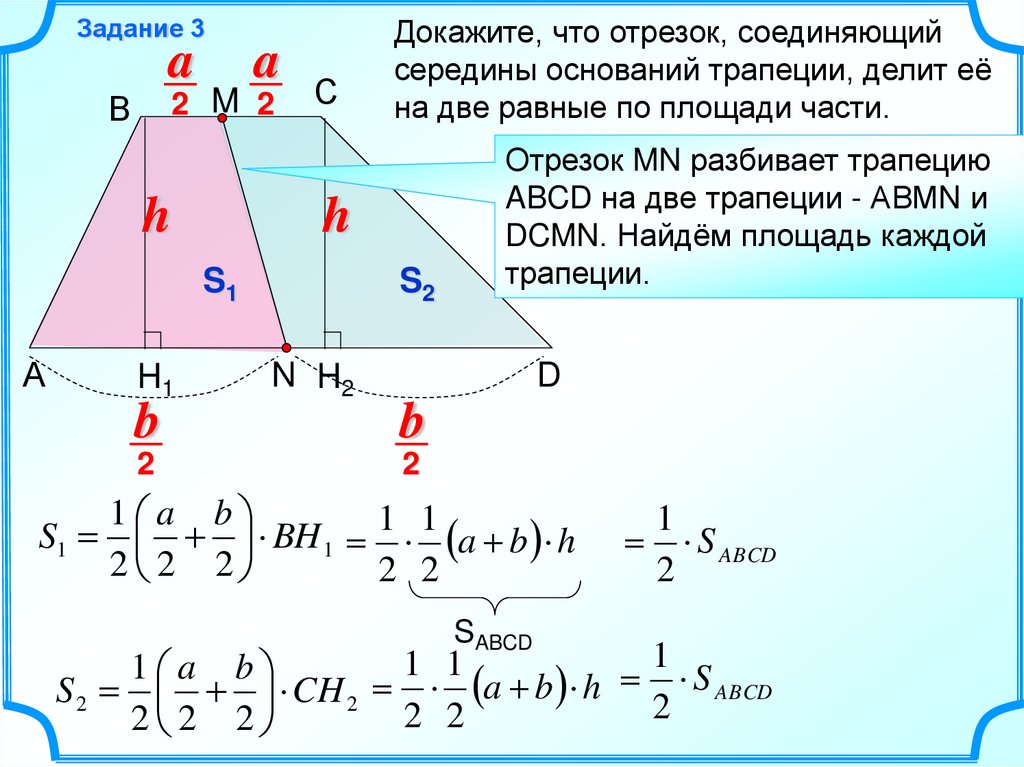
Задание 3
a
a
2 M 2
В
h
С
h
S1
А
H1
Докажите, что отрезок, соединяющий
середины оснований трапеции, делит её
на две равные по площади части.
S2
Отрезок MN разбивает трапецию
ABCD на две трапеции - АВМN и
DCMN. Найдём площадь каждой
трапеции.
N H2
D
b
b
2
2
1 a b
S1 BH 1 1 1 a b h
2 2 2
2 2
SABCD
1
S ABCD
2
1
1 1
1 a b
S 2 CH 2 a b h 2 S ABCD
2 2
2 2 2

5.

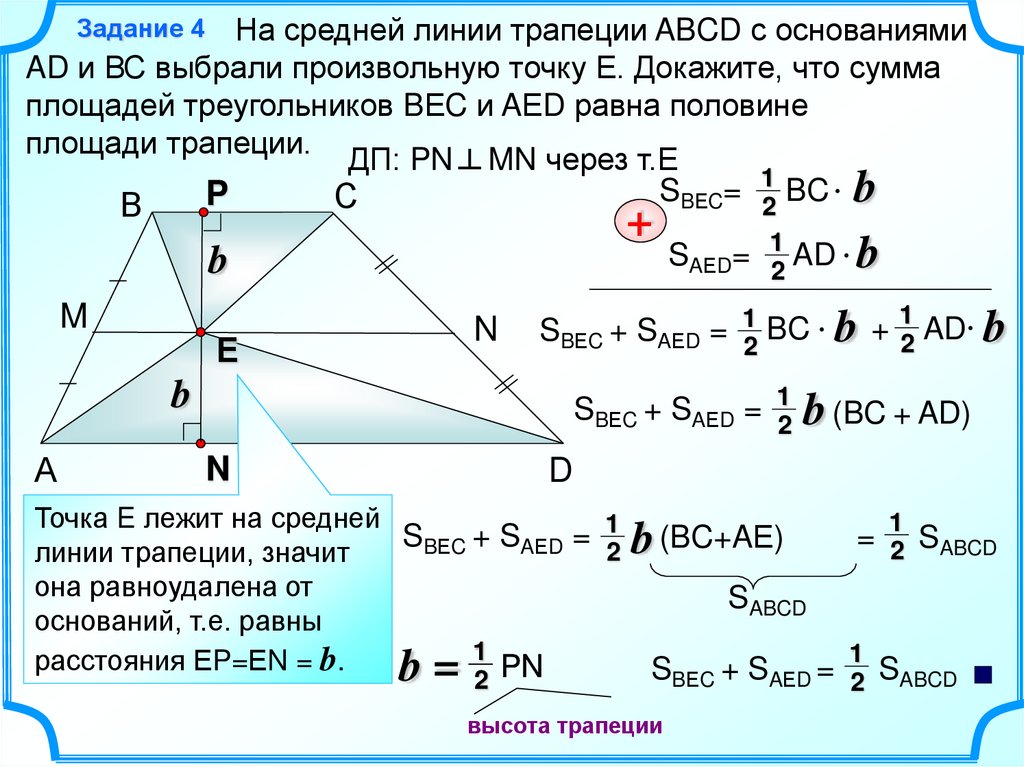
На средней линии трапеции ABCD с основаниями
AD и ВС выбрали произвольную точку Е. Докажите, что сумма
площадей треугольников BЕC и AЕD равна половине
площади трапеции.
ДП: PN ┴ MN через т.Е
SBЕC= 12 BC b
P
С
Задание 4
В
+
b
M
Е
N
SBЕC + SAЕD = 12 BC b + 2 AD b
1
b
А
SAЕD= 12 AD b
SBЕC + SAЕD = 12 b (BC + AD)
N
D
Точка E лежит на средней
1
SBЕC + SAЕD = 12 b
(BC+AЕ)
=
2 SABCD
линии трапеции, значит
она равноудалена от
SABCD
оснований, т.е. равны
1
1
расстояния ЕP=ЕN = b.
S
+S
= S
b = PN
2
высота трапеции
BЕC
AЕD
2
ABCD

6.

Задание 5
Окружность, проходящая через вершины А и В треугольника
АВС, пересекает стороны треугольника АС и ВС в точках L и К
соответственно. Докажите, что треугольники АВС и СКL подобны.
В треугольнике АМD окружность проходит через вершины А и
D, пересекает стороны треугольника АM и DM в точках B и C
соответственно. Докажите, что треугольник АMD подобен
треугольнику СMB.
Продолжения сторон СВ и DЕ вписанного в окружность
четырёхугольника ВСЕD пересекаются в точке А.
Докажите, что треугольники BDА и CAЕ подобны.
Известно, что около четырехугольника ABCD можно описать
окружность и что продолжения сторон АВ и CD
четырехугольника пересекаются в точке М. Докажите, что
треугольник МВС и MDА подобны.

7.

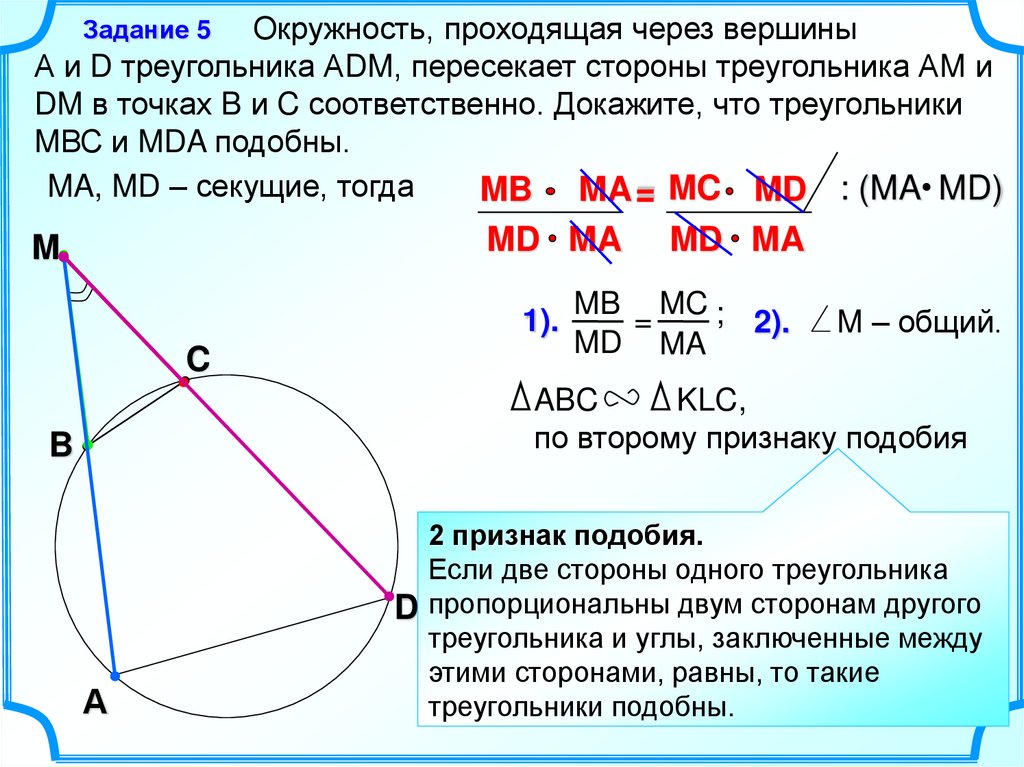
Окружность, проходящая через вершины
А и D треугольника АDM, пересекает стороны треугольника АM и
DM в точках B и C соответственно. Докажите, что треугольники
MВС и MDA подобны.
MA, MD – секущие, тогда
MB MA = MC MD : (MA MD)
Задание 5
MD MA
M
1).
C
MD MA
MB MC ;
=
2).
MD MA
M – общий.
ABC
KLC,
по второму признаку подобия
B
А
2 признак подобия.
Если две стороны одного треугольника
D пропорциональны двум сторонам другого
треугольника и углы, заключенные между
этими сторонами, равны, то такие
треугольники подобны.

8.

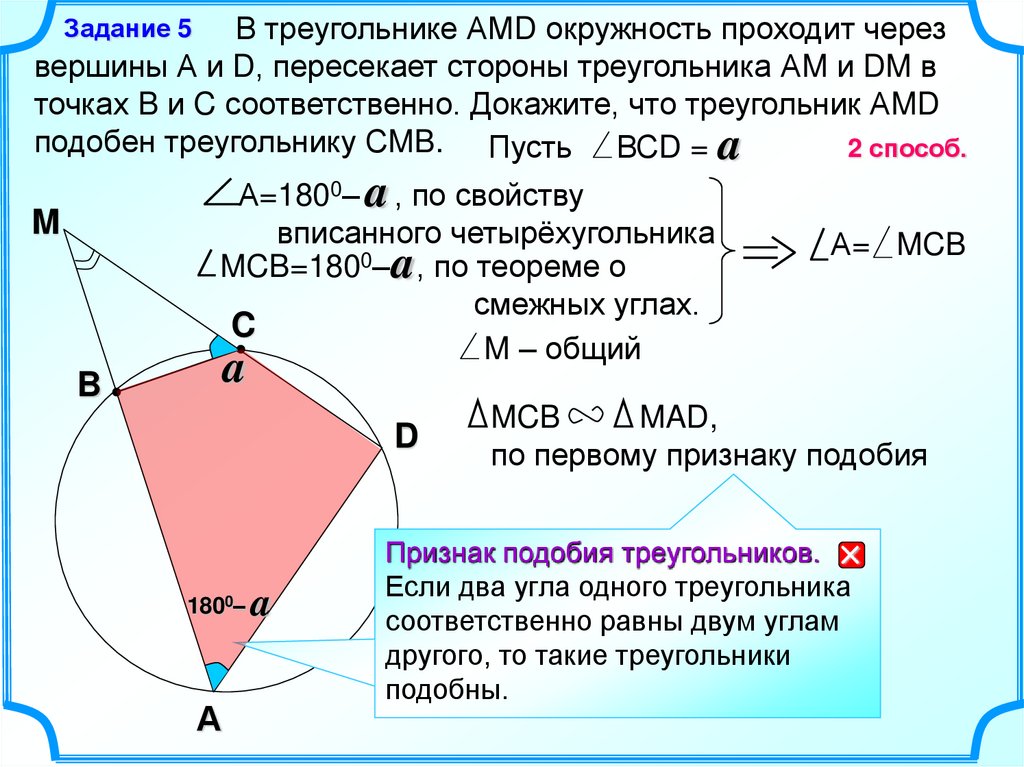
В треугольнике АМD окружность проходит через
вершины А и D, пересекает стороны треугольника АM и DM в
точках B и C соответственно. Докажите, что треугольник АMD
подобен треугольнику СMB. Пусть ВСD = a
2 способ.
Задание 5
А=1800– a , по свойству
вписанного четырёхугольника
MCB=1800– a , по теореме о
смежных углах.
C
M – общий
M
А= MCB
a
B
D
1800–
А
a
MCB
MAD,
по первому признаку подобия
Признак подобия
Свойство
углов вписанного
треугольников.
четырехугольника.
Если
два угла одного треугольника
В любом вписанном
соответственно
равны двум углам
четырехугольнике
другого,
то такие треугольники
сумма
противоположных углов равна 1800.
подобны.

9.

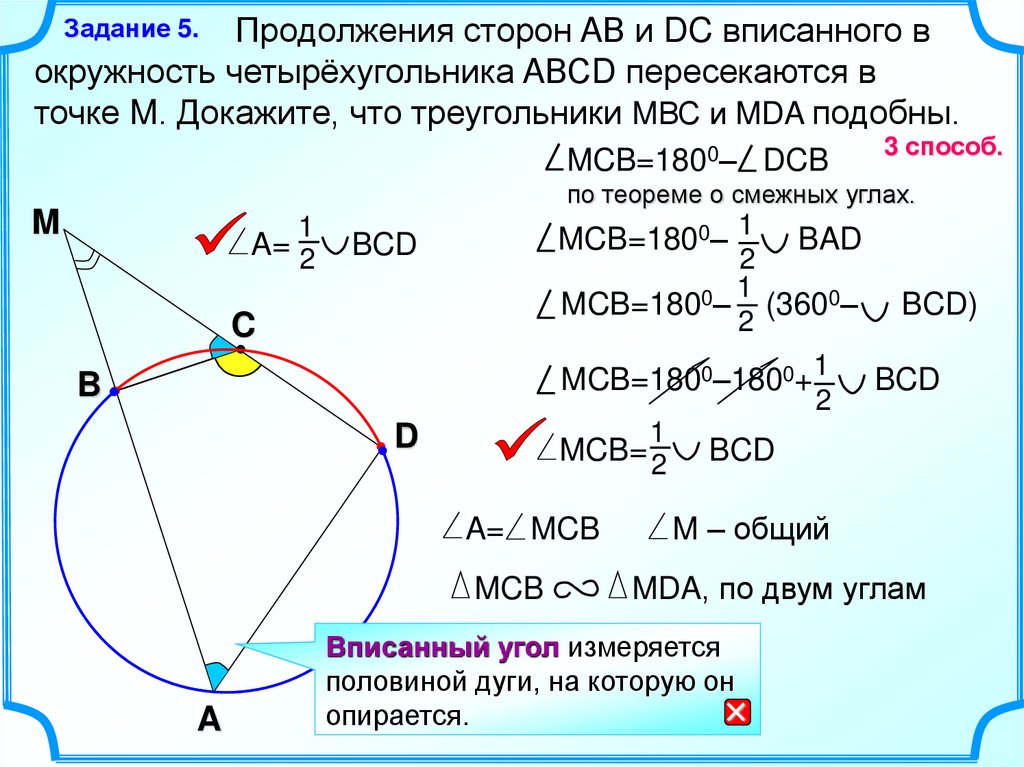
Продолжения сторон AВ и DC вписанного в
окружность четырёхугольника AВСD пересекаются в
точке M. Докажите, что треугольники MВС и MDA подобны.
Задание 5.
MCB=1800– DCB
3 способ.
по теореме о смежных углах.
M
1
A= 2
MCB=1800– 1
BCD
BAD
2
1
MCB=1800– (3600–
2
C
MCB=1800–1800+1
B
2
1
MCB= 2
D
A= MCB
MCB
A
BCD)
BCD
BCD
M – общий
MDA, по двум углам
Вписанный угол измеряется
половиной дуги, на которую он
опирается.

10.

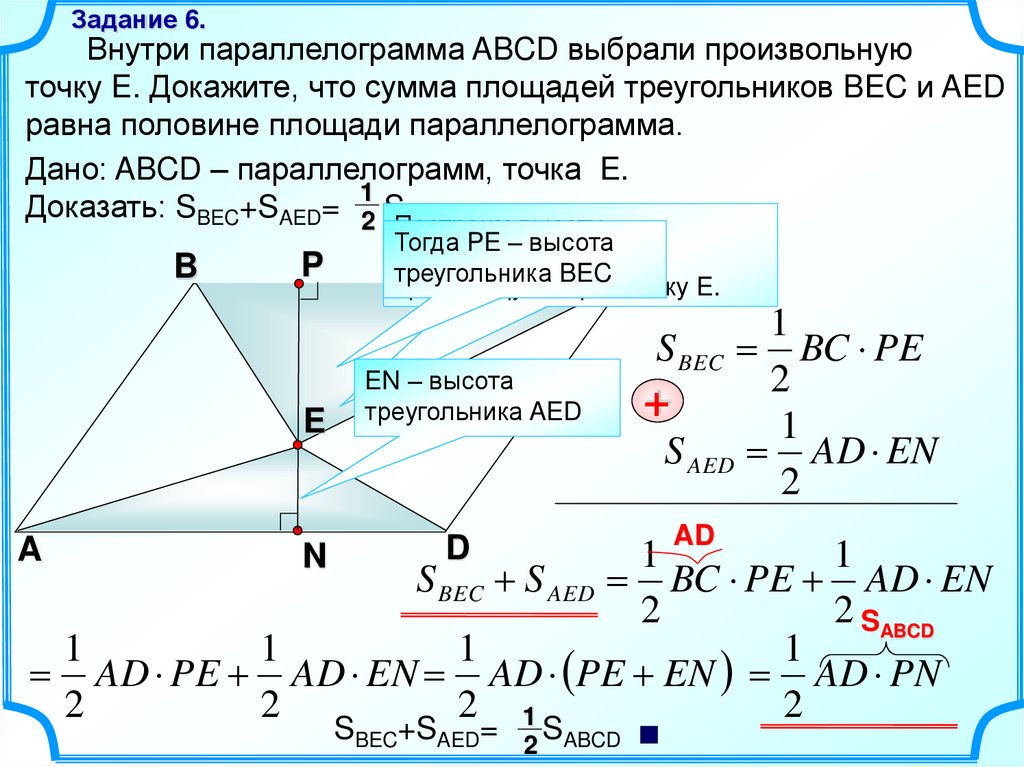
Задание 6.
Внутри параллелограмма ABCD выбрали произвольную
точку E. Докажите, что сумма площадей треугольников BEC и AED
равна половине площади параллелограмма.
Дано: ABCD – параллелограмм, точка E.
1
Доказать: SBEC+SAED= 2 SABCD.
B
P
E
A
Построим высоту
Тогда PE – высота
параллелограмма, C
треугольника BEC
проходящую через точку E.
EN – высота
треугольника AED
D
1
S BEC BC PE
2
+
1
S AED AD EN
2
AD
1
1
S BEC S AED BC PE AD EN
2
2 SABCD
1
1
1
1
AD PE AD EN AD PE EN AD PN
2
2
2 1
2
N
SBEC+SAED= 2 SABCD

11.

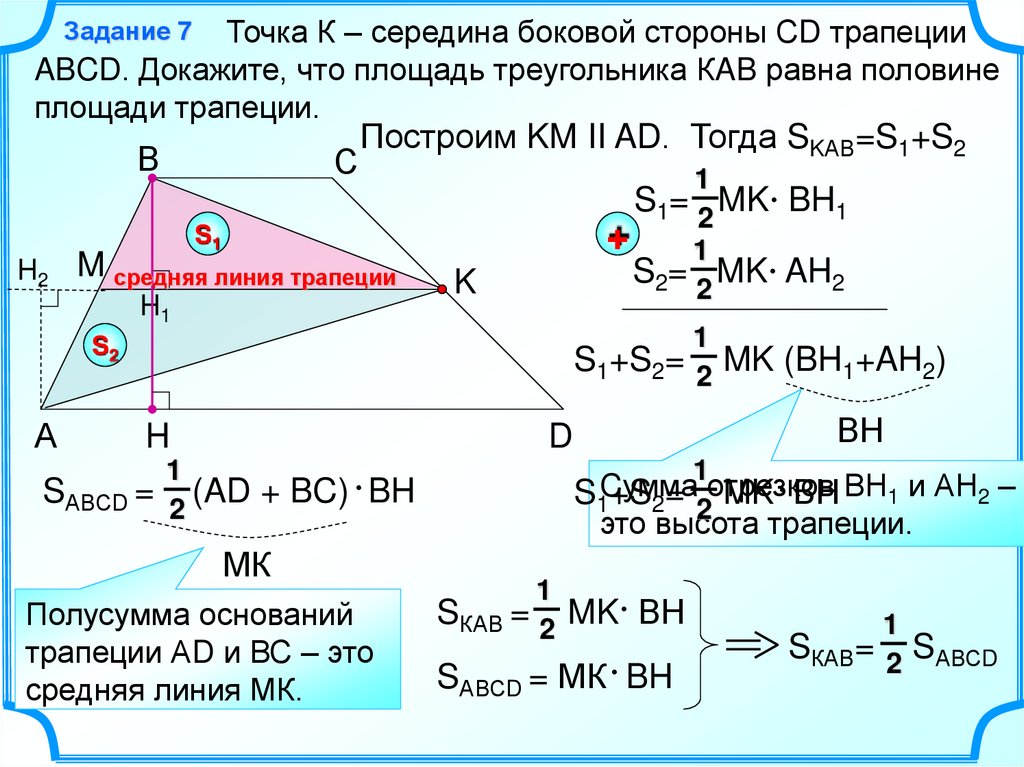
Точка К – середина боковой стороны СD трапеции
ABCD. Докажите, что площадь треугольника КAB равна половине
площади трапеции.
Задание 7
В
С
Построим KM II AD. Тогда SKАВ=S1+S2
1
S1= 2 MK BH1
+
1
S2= 2 MK AH2
S1
H2
M средняя линия трапеции
H1
K
1
S1+S2= 2 MK (BH1+AH2)
S2
А
H
ВН
D
1
SАВСD = 2 (AD + BC) BH
МК
Полусумма оснований
трапеции АD и ВС – это
средняя линия МК.
1
S1Cумма
+S2= 2отрезков
MK ВН ВН1 и АН2 –
это высота трапеции.
1
SКАВ = 2 MK ВН
SАВСD = МК BH
1
SКАВ= 2 SАВСD

12.

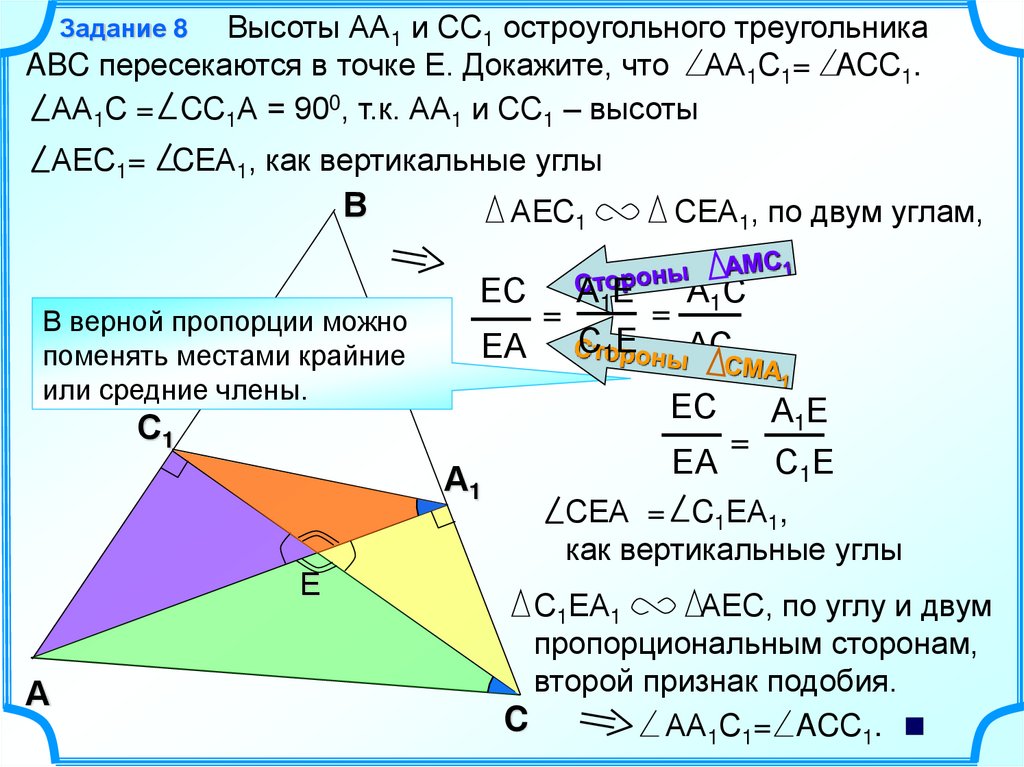
Высоты АА1 и СС1 остроугольного треугольника
ABC пересекаются в точке Е. Докажите, что АА1С1= ACС1.
АА1С = CС1А = 900, т.к. АА1 и СС1 – высоты
Задание 8
АЕС1= CЕА1, как вертикальные углы
В
В верной пропорции можно
поменять местами крайние
или средние члены.
АЕС1
ЕС
А1Е
А1С
=
=
ЕА С1Е АС1
ЕС
С1
А1
Е
А
СЕА1, по двум углам,
А1Е
=
ЕА
С1Е
СЕА = C1ЕА1,
как вертикальные углы
С1ЕА1
АЕС, по углу и двум
пропорциональным сторонам,
второй признак подобия.
C
АА1С1= ACС1.

13.

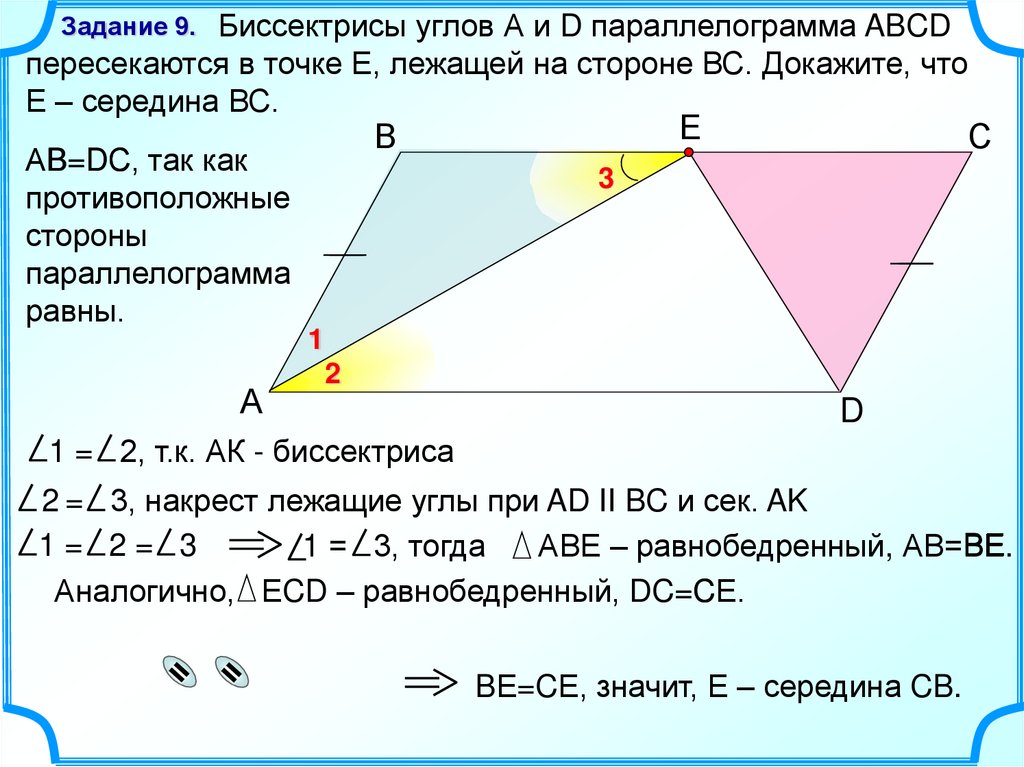
Биссектрисы углов А и D параллелограмма ABCD
пересекаются в точке Е, лежащей на стороне ВС. Докажите, что
Е – середина ВС.
Задание 9.
Е
В
АB=DС так как
АB=DС,
противоположные
стороны
параллелограмма
равны.
С
3
1
А
2
D
1 = 2, т.к. АК - биссектриса
2 = 3, накрест лежащие углы при AD II BC и сек. AK
1= 2= 3
BЕ
1 = 3, тогда
АВЕ – равнобедренный, АВ=ВЕ.
Аналогично, ЕCD – равнобедренный, DC=CЕ.
=СЕ
BЕ=CЕ, значит, Е – середина CB.

14.

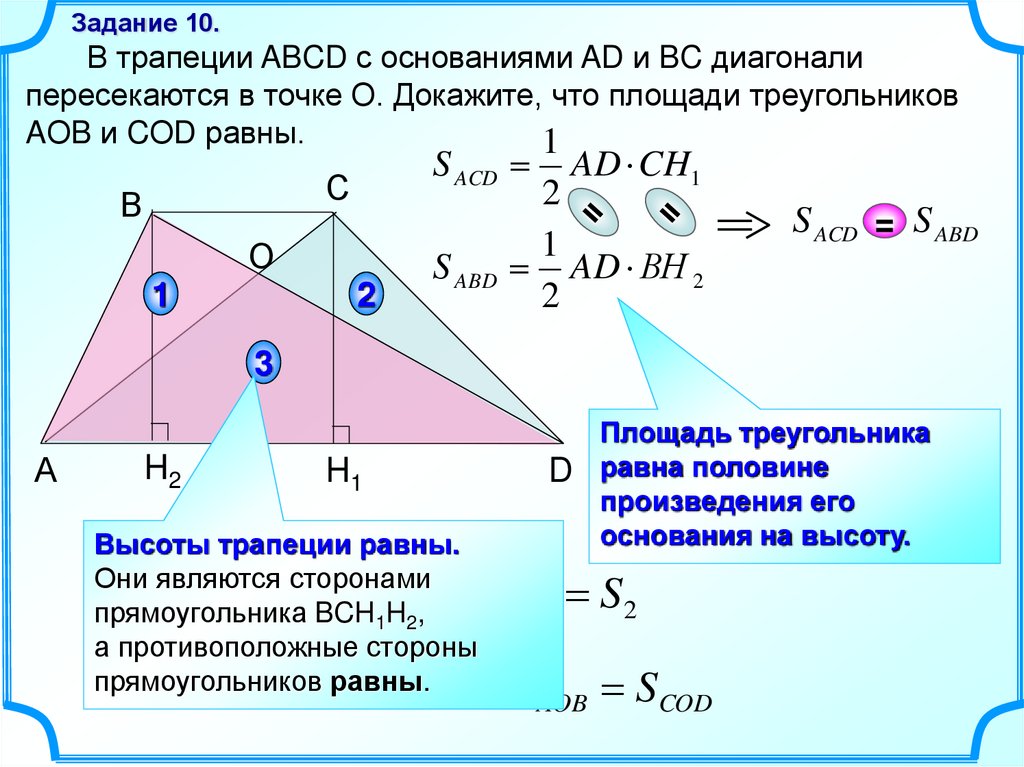
Задание 10.
В трапеции ABCD с основаниями AD и BC диагонали
пересекаются в точке О. Докажите, что площади треугольников
AОB и CОD равны.
1
S ACD
С
В
О
1
2
AD CH1
2
1
S ABD AD ВH 2
2
S ACD
= S ABD
3
А
H2
H1
Высоты трапеции равны.
S ACD сторонами
S 2 S3
Они являются
прямоугольника BCH1H2,
S ABD S1 стороны
S3
а противоположные
прямоугольников равны.
Площадь треугольника
D равна половине
произведения его
основания на высоту.
S1 S2
S AOB SCOD

15.

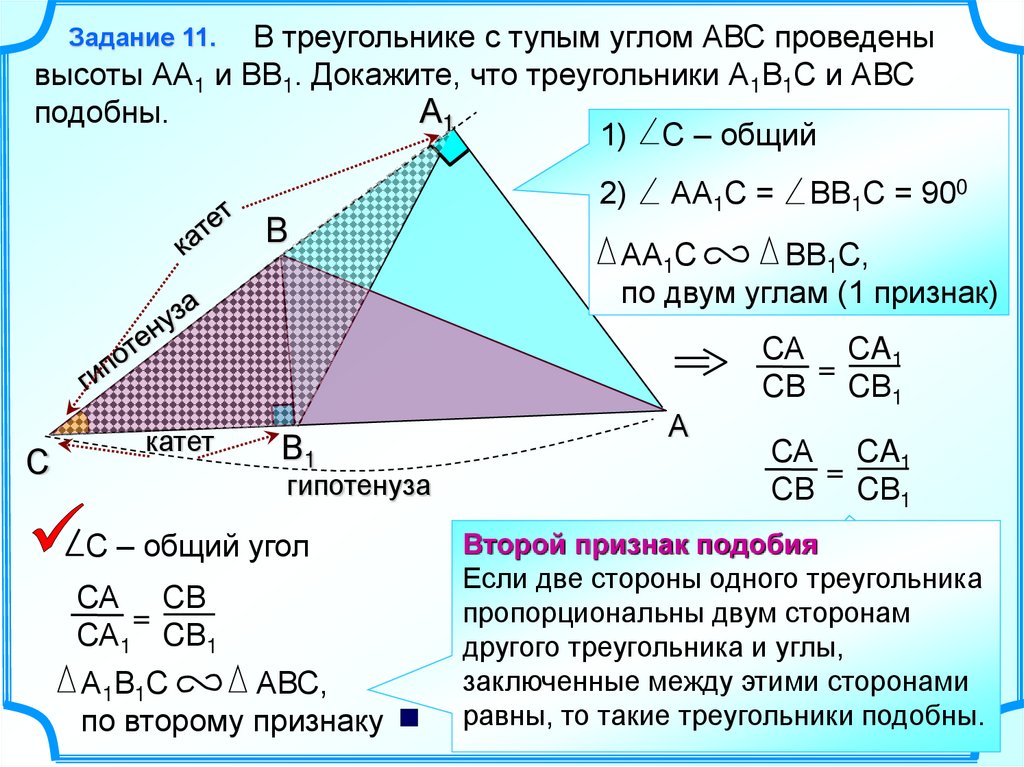
В треугольнике с тупым углом АВС проведены
высоты АА1 и ВВ1. Докажите, что треугольники А1В1С и АВС
А1
подобны.
1) С – общий
Задание 11.
2)
B
С
катет
В1
гипотенуза
С – общий угол
СА СВ
=
СА1 CВ1
А1В1С
АВС,
по второму признаку
АА1С =
ВВ1С = 900
АА1С
ВВ1С,
по двум углам (1 признак)
А
СА СA1
=
СВ CВ1
СА СA1
=
СВ CВ1
Второй признак подобия
Если двеСвойство
стороны одного
треугольника
пропорции.
пропорциональны
двум пропорции
сторонам
Если в верной
другого треугольника
и углы,средние
поменять местами
заключенные
между
этими сторонами
члены,
то получим
верную
равны, топропорцию.
такие треугольники подобны.

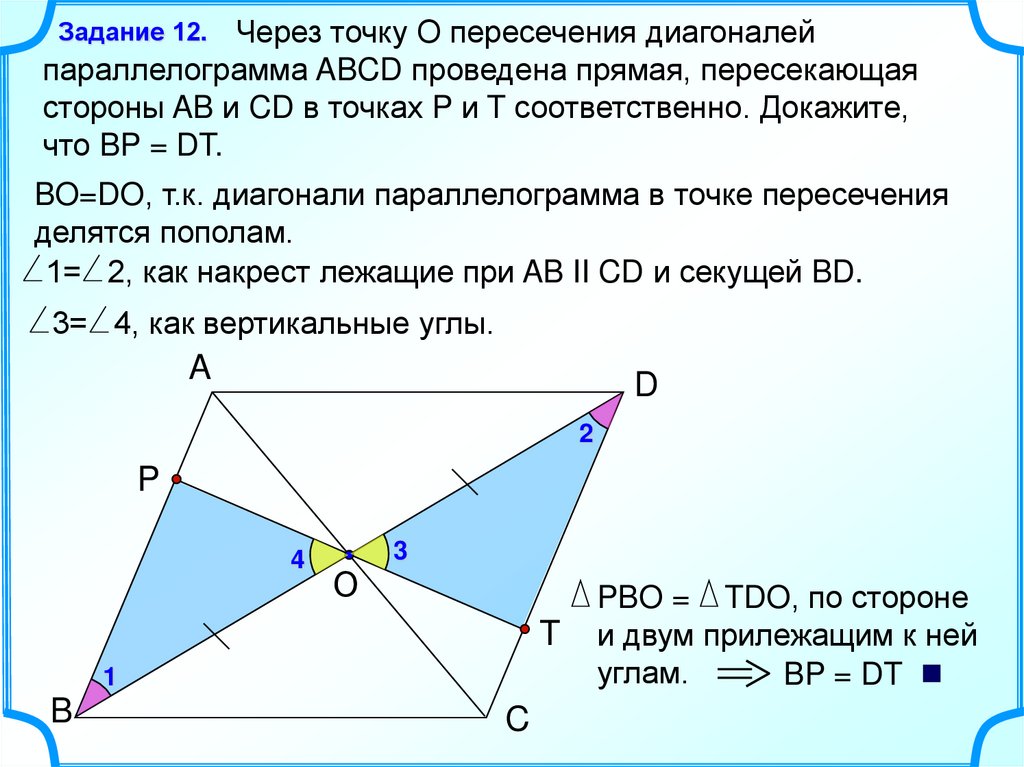
16.

Через точку О пересечения диагоналей
параллелограмма ABCD проведена прямая, пересекающая
стороны AB и CD в точках P и T соответственно. Докажите,
что BP = DT.
Задание 12.
BO=DO, т.к. диагонали параллелограмма в точке пересечения
делятся пополам.
1= 2, как накрест лежащие при AB II CD и секущей BD.
3= 4, как вертикальные углы.
A
D
2
P
4
3
О
T
1
B
C
PBO = TDO, по стороне
и двум прилежащим к ней
углам.
BP = DT

17.

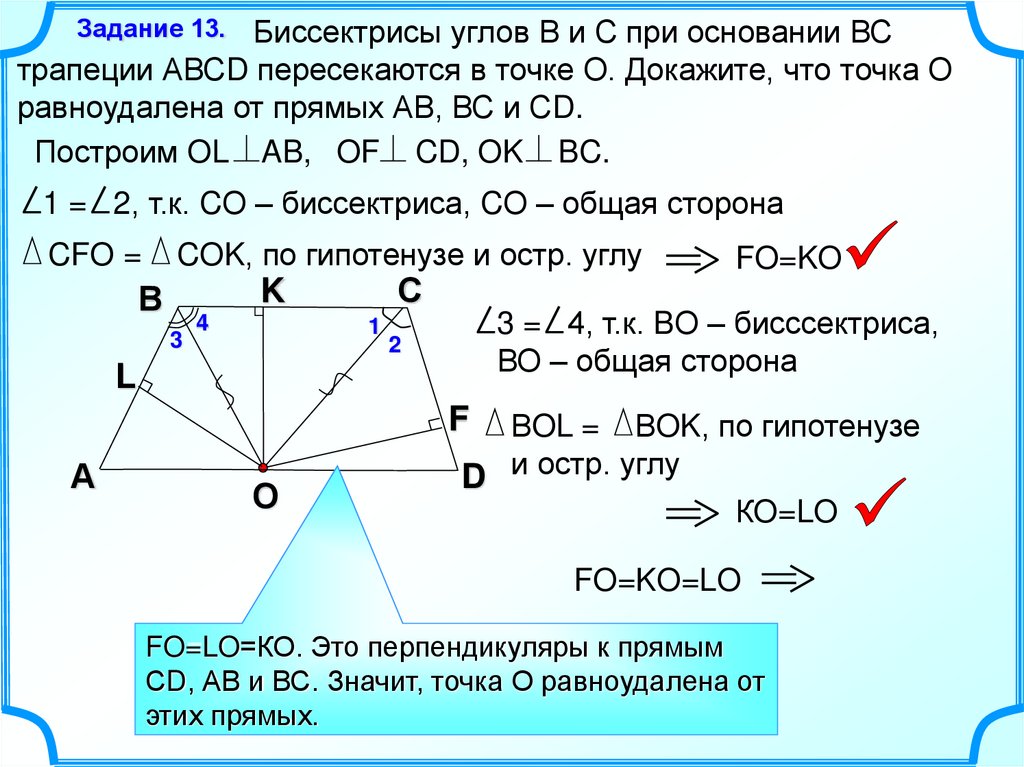
Задание 13.
Биссектрисы углов В и С при основании ВС
трапеции АВСD пересекаются в точке О. Докажите, что точка О
равноудалена от прямых АВ, ВС и СD.
Построим OL AB, OF CD, OK BC.
1 = 2, т.к. CО – биссектриса, CО – общая сторона
COK, по гипотенузе и остр. углу
CFO =
С
K
В
3
4
1
FO=KO
3 = 4, т.к. BО – бисссектриса,
ВО – общая сторона
2
L
F
А
О
ВOL = ВOK, по гипотенузе
D и остр. углу
КO=LO
FO=KO=LO
FO=LO=КО. Это перпендикуляры к прямым
СD, АВ и ВС. Значит, точка О равноудалена от
этих прямых.

18.

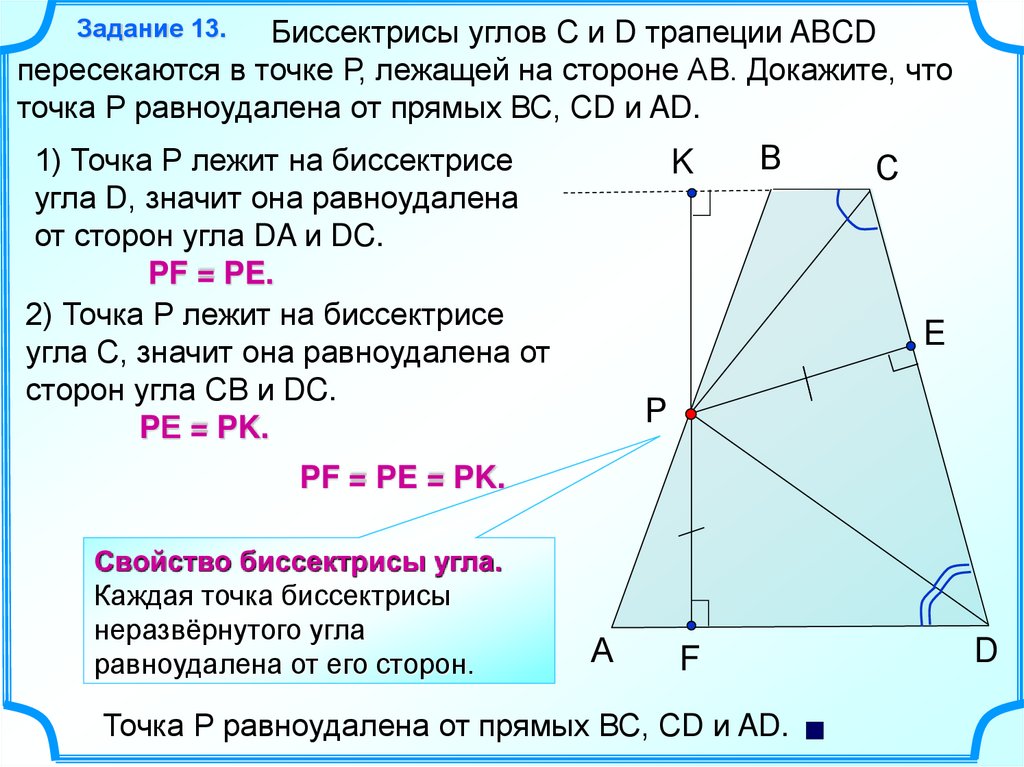
Задание 13.
Биссектрисы углов С и D трапеции ABCD
пересекаются в точке Р, лежащей на стороне АВ. Докажите, что
точка Р равноудалена от прямых ВС, СD и AD.
1) Точка Р лежит на биссектрисе
угла D, значит она равноудалена
от сторон угла DA и DC.
PF = PE.
2) Точка Р лежит на биссектрисе
угла С, значит она равноудалена от
сторон угла СВ и DC.
PЕ = PK.
K
В
С
E
Р
PF = PE = PK.
Свойство биссектрисы угла.
Каждая точка биссектрисы
неразвёрнутого угла
равноудалена от его сторон.
А
F
Точка Р равноудалена от прямых ВС, СD и AD.
D

19.

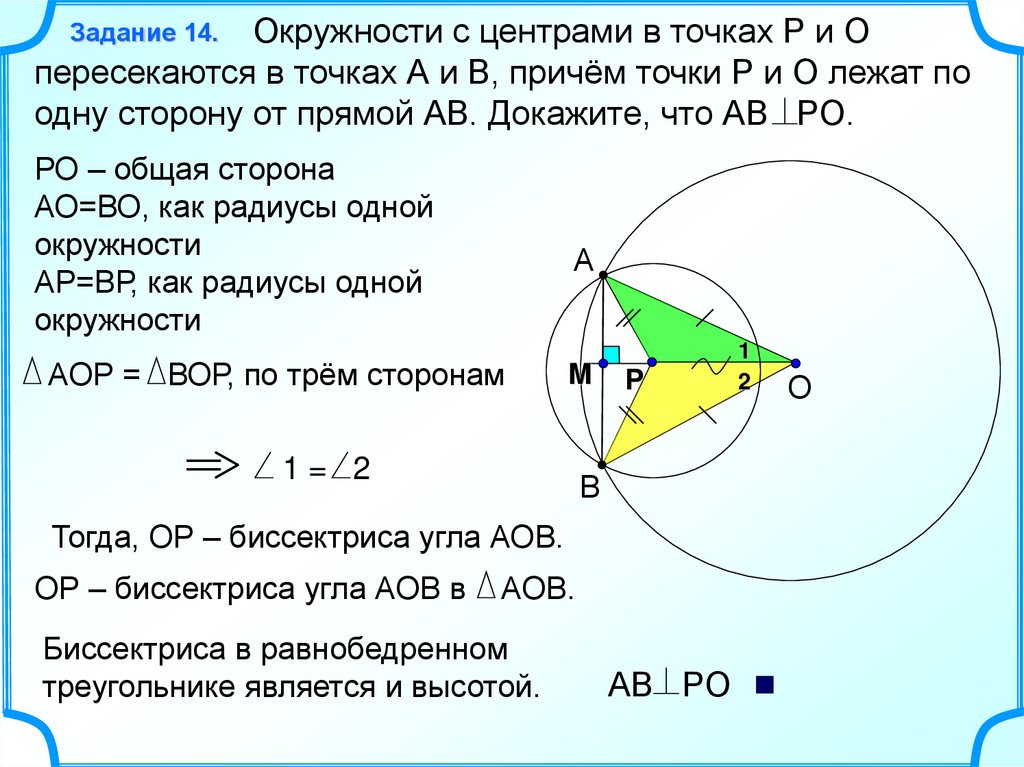
Окружности с центрами в точках Р и О
пересекаются в точках А и В, причём точки Р и О лежат по
одну сторону от прямой АВ. Докажите, что АВ РО.
Задание 14.
РО – общая сторона
АО=ВО, как радиусы одной
окружности
АР=ВР, как радиусы одной
окружности
А
АОР = ВОР, по трём сторонам
M
1= 2
Р
В
Тогда, ОР – биссектриса угла АОВ.
ОР – биссектриса угла АОВ в
АОВ.
Биссектриса в равнобедренном
треугольнике является и высотой.
АВ РО
1
2
О

20.

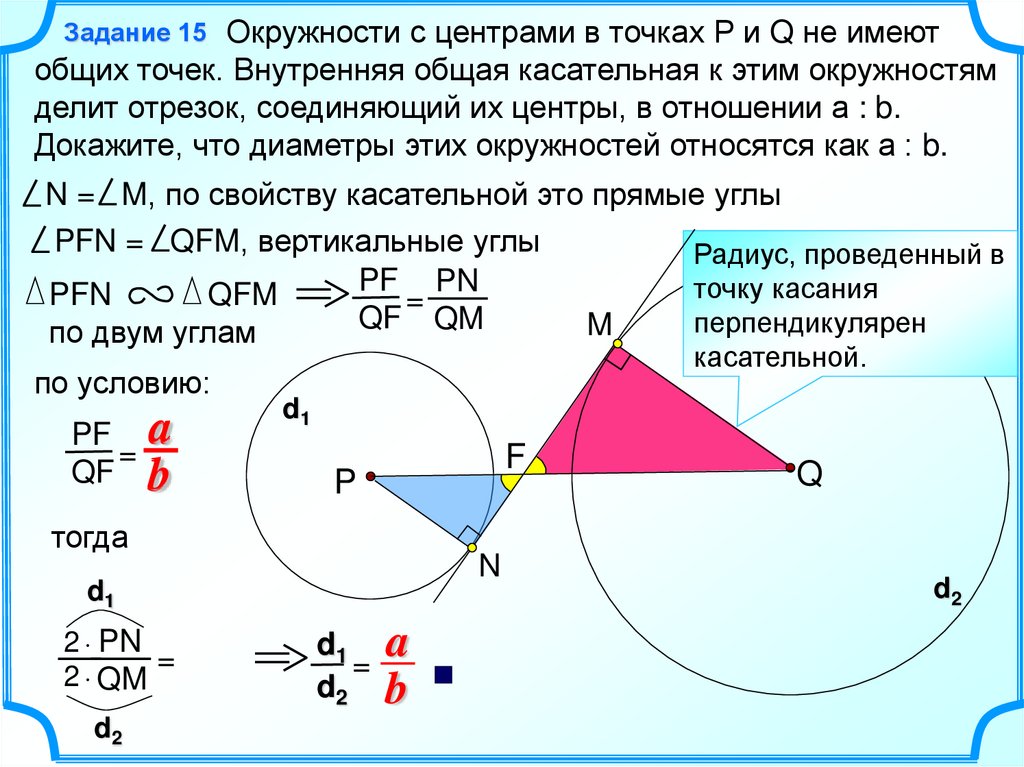
Окружности с центрами в точках Р и Q не имеют
общих точек. Внутренняя общая касательная к этим окружностям
делит отрезок, соединяющий их центры, в отношении а : b.
Докажите, что диаметры этих окружностей относятся как а : b.
Задание 15
N = M, по свойству касательной это прямые углы
PFN = QFM, вертикальные углы
Радиус, проведенный в
PF PN
точку касания
PFN
QFM
=
QF QM
перпендикулярен
M
по двум углам
по условию:
PF a
=
QF b
касательной.
d1
P
тогда
N
d1
2 PN
=
2 QM
d2
F
d1 a
=
d2 b
Q
d2

21.

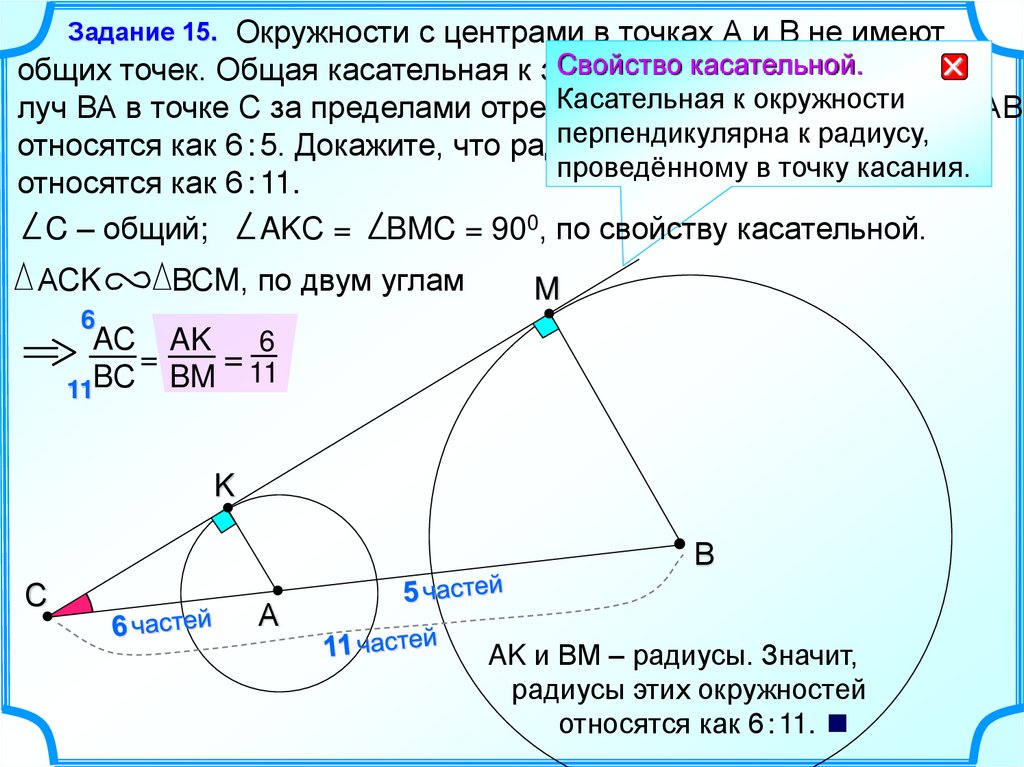
Окружности с центрами в точках А и В не имеют
Cвойство
касательной.
общих точек. Общая касательная к этим
окружностям
пересекает
Касательная
к окружности
луч ВА в точке С за пределами отрезка
АВ. Длины
отрезков АС и АВ
перпендикулярна
к радиусу,
относятся как 6 : 5. Докажите, что радиусы
этих окружностей
проведённому в точку касания.
относятся как 6 : 11.
C – общий;
AKС = BMC = 900, по свойству касательной.
Задание 15.
АСK
ВСM, по двум углам
M
6
AС AK
6
=
= 11
BM
BС
11
K
В
С
А
AK и ВМ – радиусы. Значит,
радиусы этих окружностей
относятся как 6 : 11.

22.

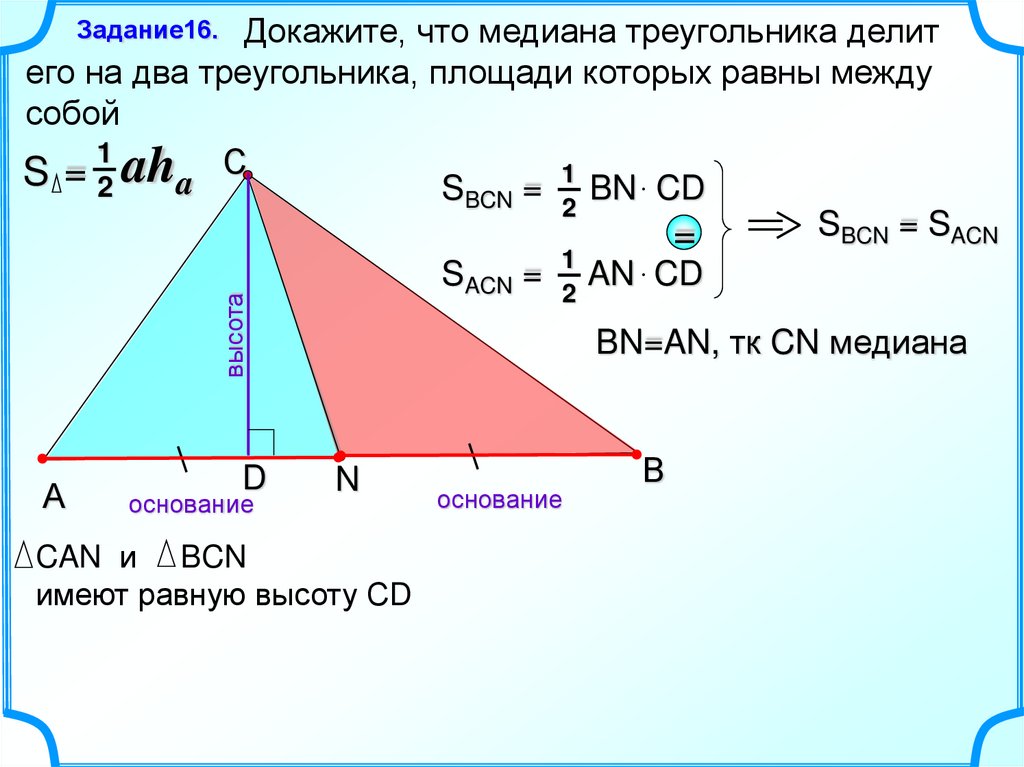
Докажите, что медиана треугольника делит
его на два треугольника, площади которых равны между
собой
1
S = 2 aha С
SBCN = 1 BN CD
2
SBCN = SACN
=
SACN = 1 AN CD
Задание16.
высота
2
А
D
основание
BN=AN, тк CN медиана
N
CAN и BCN
имеют равную высоту СD
основание
В

23.

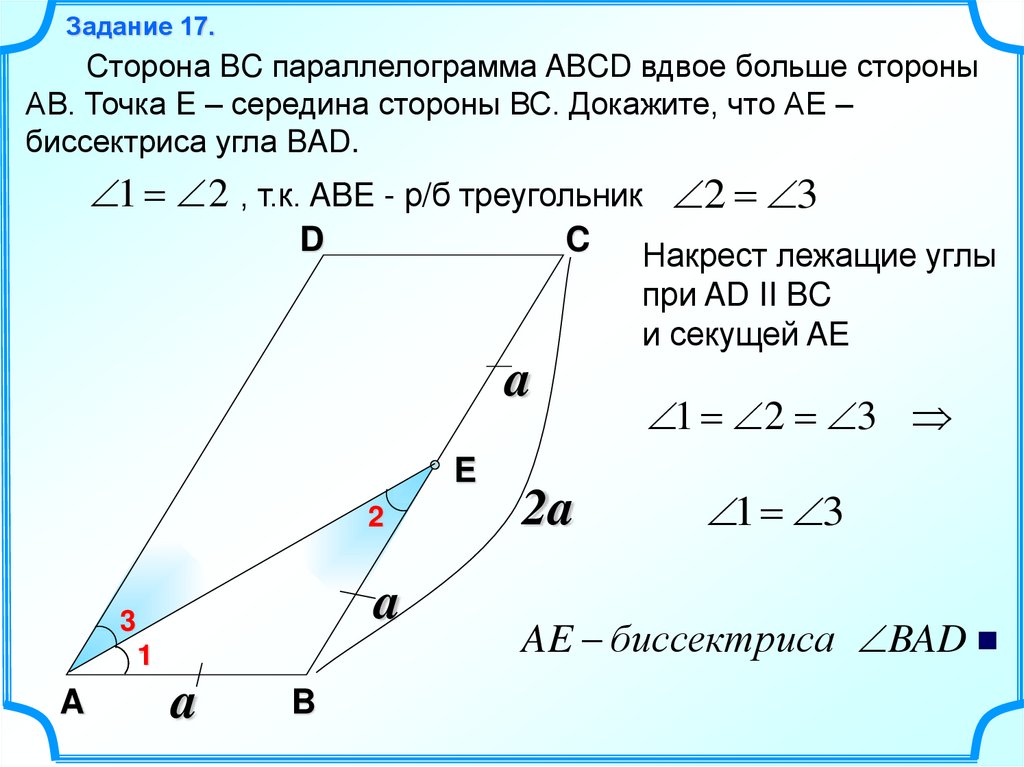
Задание 17.
Сторона BC параллелограмма ABCD вдвое больше стороны
АВ. Точка E – середина стороны ВС. Докажите, что АЕ –
биссектриса угла BAD.
1 2 , т.к. ABE - р/б треугольник 2 3
D
C
a
E
2
a
3
1
A
a
B
2a
Накрест лежащие углы
при AD II BC
и секущей AE
1 2 3
1 3
AE биссектриса BAD

24.

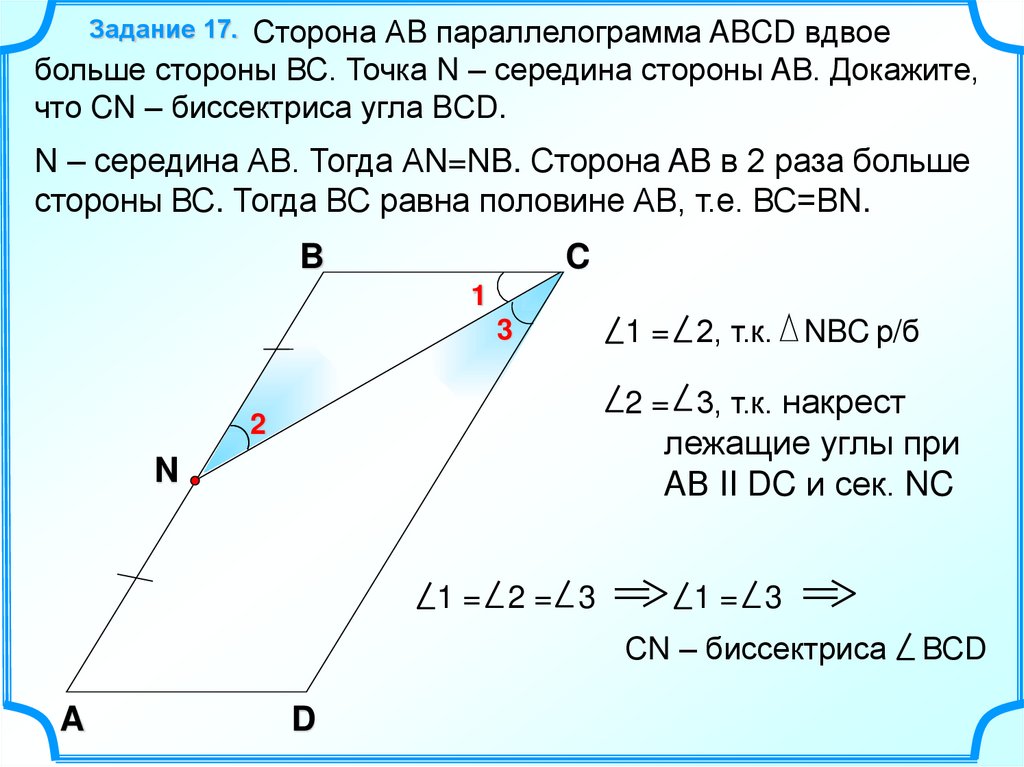
Задание 17. Сторона АB параллелограмма ABCD вдвое
больше стороны ВС. Точка N – середина стороны AВ. Докажите,
что CN – биссектриса угла BСD.
N – середина АВ. Тогда АN=NB. Сторона AB в 2 раза больше
стороны ВС. Тогда ВС равна половине АВ, т.е. ВС=ВN.
B
C
1
3
1 = 2, т.к. NBC р/б
2 = 3, т.к. накрест
2
лежащие углы при
AВ II DC и сек. NC
N
1= 2= 3
1= 3
СN – биссектриса
A
D
ВСD