Оценка сложности (эффективности) алгоритмов

1.

Оценка сложности (эффективности) алгоритмов
Лабораторная работа № 1
1. Основы расчетов временной сложности
2. Асимптотическая оценка эффективности
3. Правила оценки асимптотической сложности
4. Несколько примеров оценок сложности
5. Индивидуальные задания
1

2.

Оценки трудозатрат для элементарных операций
Для определения временной сложности алгоритма обычно
используют набор «элементарных» операций, характерных для
языков высокого уровня.
Для этого выделим ряд простейших операций высокого уровня,
которые в целом не зависят от используемого языка
программирования и могут использоваться в псевдокоде:
• присваивание переменной значения,
• вызов метода,
• выполнение арифметической операции (например, сложение
двух чисел),
• сравнение двух чисел,
• индексация массива,
• переход по ссылке,
• вызов метода
• возвращение из метода.
2

3.

Будем считать их длительность – 1 такт
1.1. Простое присваивание: а=b, будем считать ее сложность, равной
постоянной с=1;
1.2. Одномерная индексация a[i]: (адрес (a)+i*длина элемента),
сложность считается постоянной и равной 2;
1.3. Арифметические операции: (*, /, -, +), сложность считается
равной 1
1.4. Операции сравнения: a < b, сложность считается равной 1;
1.5. Логические операции or, and, not сложность считается равной 1
1.6. Переход (команда Goto) – 1 такт
Длительность зависит от количества аргументов на входе и выходе
1.7. Вызов метода (функции) - 1 такт переход
+к-тактов - загрузка к-аргументов
1.8. Возврат результатов - вызов метода - 1 такт переход
+к-тактов - загрузка к-результатов
3

4.

1.2. Оценки сложности основных управляющих конструкций
Доказано, что любую программу можно написать, используя
комбинации трех базовых структур
• последовательность команд (операторов, инструкций)
• ветвление (условный) оператор
• повторение или цикл (оператор)
Новые программные структуры
мы можем построить на основе приведенных выше.
4

5.

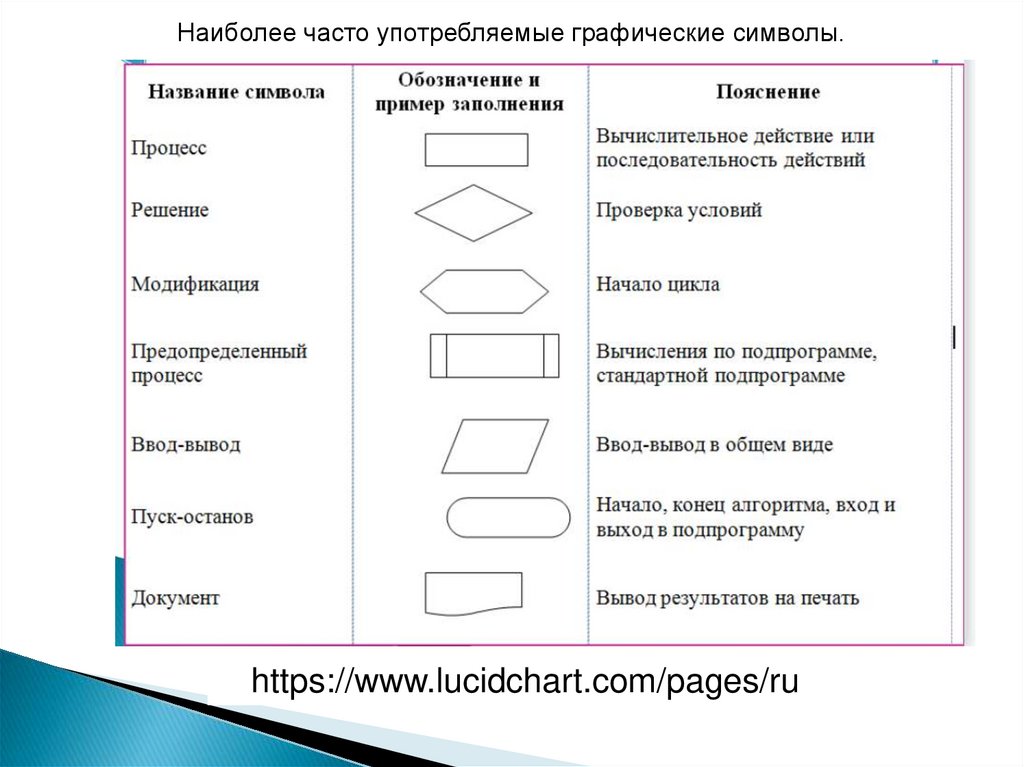
Наиболее часто употребляемые графические символы.
https://www.lucidchart.com/pages/ru

6.

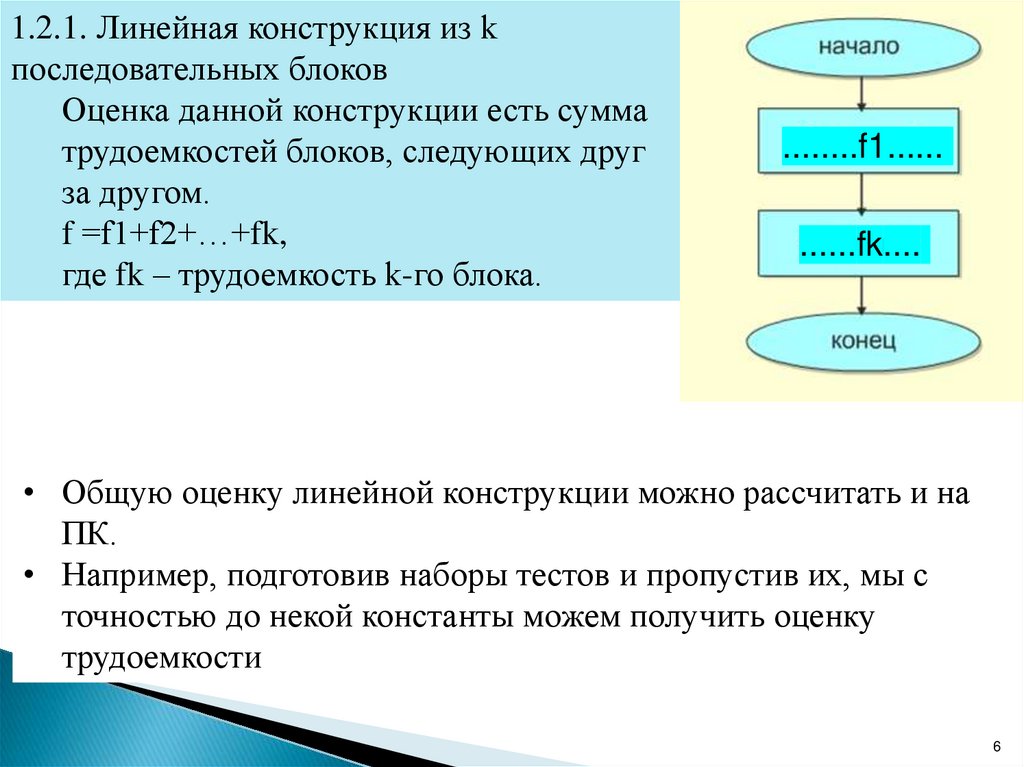
1.2.1. Линейная конструкция из k
последовательных блоков
Оценка данной конструкции есть сумма
трудоемкостей блоков, следующих друг
за другом.
f =f1+f2+…+fk,
где fk – трудоемкость k-го блока.
........f1......
......fk....
• Общую оценку линейной конструкции можно рассчитать и на
ПК.
• Например, подготовив наборы тестов и пропустив их, мы с
точностью до некой константы можем получить оценку
трудоемкости
6

7.

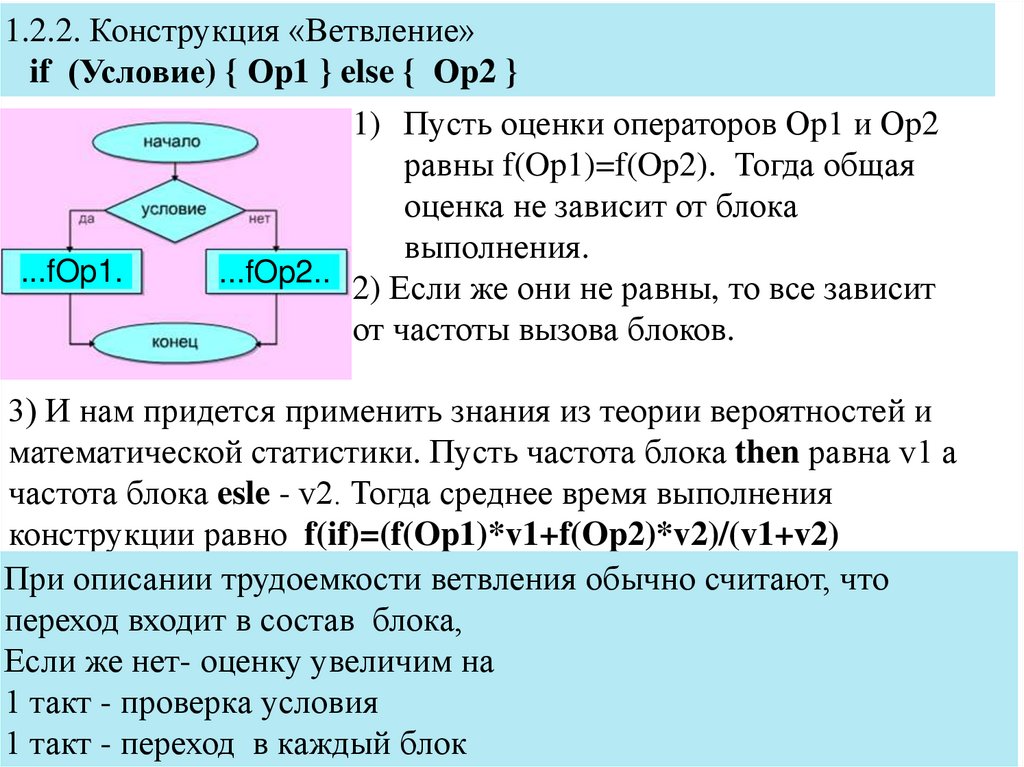
1.2.2. Конструкция «Ветвление»
if (Условие) { Оp1 } else { Оp2 }
...fOp1.
1) Пусть оценки операторов Оp1 и Оp2
равны f(Op1)=f(Op2). Тогда общая
оценка не зависит от блока
выполнения.
...fOp2..
2) Если же они не равны, то все зависит
от частоты вызова блоков.
3) И нам придется применить знания из теории вероятностей и
математической статистики. Пусть частота блока then равна v1 а
частота блока esle - v2. Тогда среднее время выполнения
конструкции равно f(if)=(f(Op1)*v1+f(Op2)*v2)/(v1+v2)
При описании трудоемкости ветвления обычно считают, что
переход входит в состав блока,
Если же нет- оценку увеличим на
1 такт - проверка условия
1 такт - переход в каждый блок
7

8.

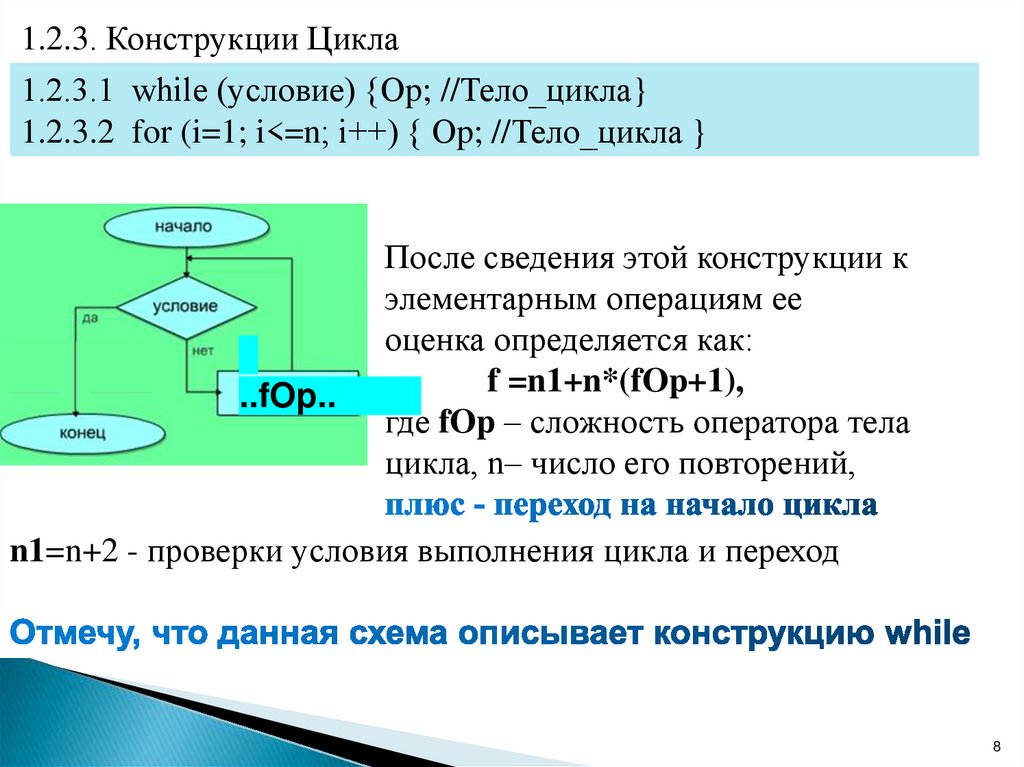
1.2.3. Конструкции Цикла
1.2.3.1 while (условие) {Оp; //Тело_цикла}
1.2.3.2 for (i=1; i<=n; i++) { Оp; //Тело_цикла }
..fOp..
После сведения этой конструкции к
элементарным операциям ее
оценка определяется как:
f =n1+n*(fOp+1),
где fOp – сложность оператора тела
цикла, n– число его повторений,
n1=n+2 - проверки условия выполнения цикла и переход
8

9.

2.3.2 Для конструкций цикла for (k=0;k<n;k++) {fOp}
• к=0 - 1 такт
• условие - 1 такт
• переход - 1 такт
• тело цикла - fOp
• увеличение счетчика - k++ - это 2 такта
• переход на начало цикла – 1 такт
Итого: 1+5
Нам не будет особой необходимости рассчитывать точное
количество тактов, так как в каждой среде они будут отличаться, да
и в литературе приводят упрощенный способ расчета.
- мы будет отталкиваться от блок - схемы
- для нас будет важна асимптотическая оценка, с которой
познакомимся позже
- и здесь погрешности в количестве тактов не влияют на результат
9

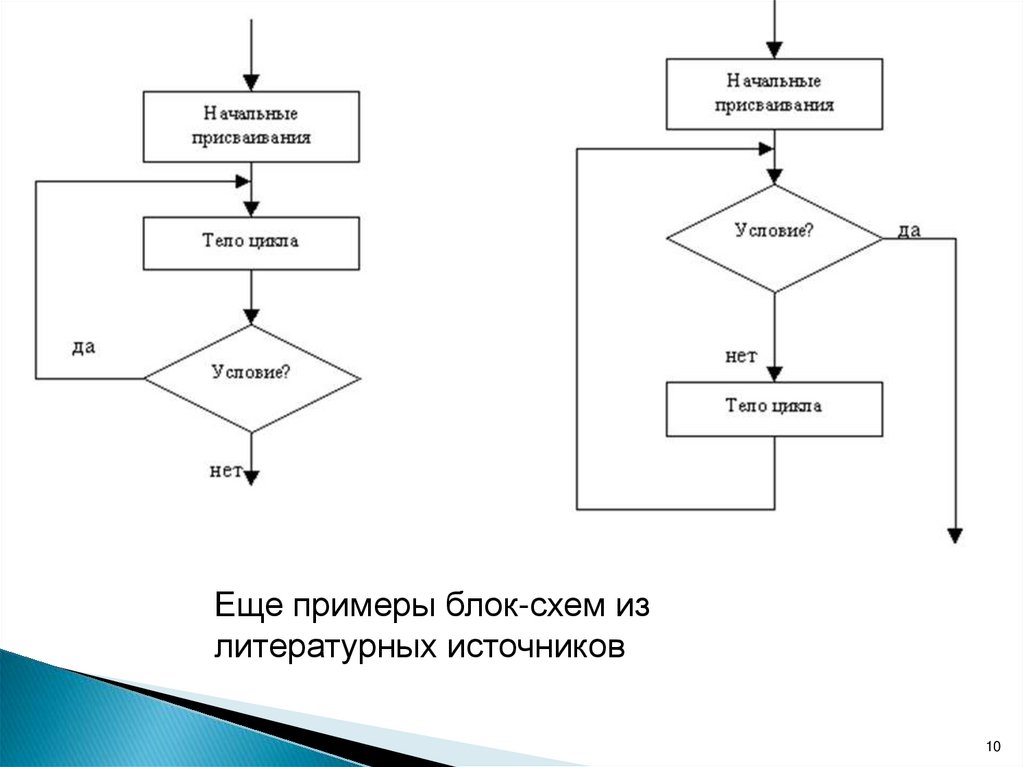
10.

Еще примеры блок-схем из
литературных источников
10

11.

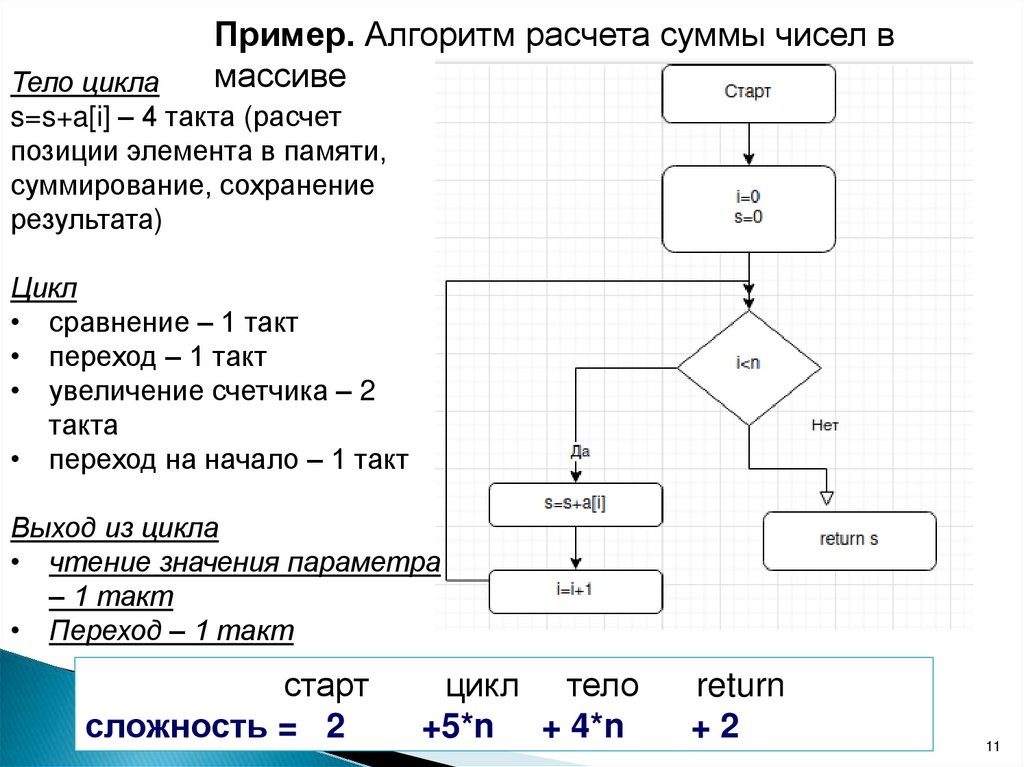
Пример. Алгоритм расчета суммы чисел в
массиве
Тело цикла
s=s+a[i] – 4 такта (расчет
позиции элемента в памяти,
суммирование, сохранение
результата)
Цикл
• сравнение – 1 такт
• переход – 1 такт
• увеличение счетчика – 2
такта
• переход на начало – 1 такт
Выход из цикла
• чтение значения параметра
– 1 такт
• Переход – 1 такт
старт
сложность = 2
цикл тело
+5*n + 4*n
return
+2
11

12.

2. Асимптотическая оценка эффективности
Для анализа скорости алгоритмов используют теоретические
методы, главным из которых является метод асимптотической
оценки временной эффективности
Вернемся к предыдущему примеру – расчета суммы элементов
массива.
Если размер массива n взять как параметр, то длительность всего
блока - 2+5*n+ 4*n+ 2 = 4+9*n
При стремлении n к бесконечности график функции f(n)
асимптотически стремится к n (с точностью до некоторой
константы), в нашем случае константа равна 9.
Отсюда следует вывод - оценка поиска элемента в обычном массиве
асимптотически стремится к n.
12

13.

В зависимости от эффективности существует много типов
алгоритмов, среди которых можно выделить следующие типы
алгоритмов:
Константный О(1)
Линейный О(N)
Квадратичный О(N2)
Полиномиальный (N**m)
Логарифмический О(logN)
Линейно-логарифмический О(N*logN)
Экспоненциальная сложность O(2**N)
Несколько простых примеров

14.

• Константный О(1) – прямая выборка из массива.
Например, извлечение А[k] сводится к операциям
расчет позиции элемента - k*s где s - размер элемента.
расчет адреса элемента адрес = адрес массива+позиция
элемента
извлечение элемента
Общая длительность зависит только от указанных трех операций с
общей длительностью О(1) с точностью до константы.
Следует отметить, что алгоритм, не имеющий циклов и рекурсий
можно смело отнести к алгоритмам с оценкой О(1)
14

15.

• Линейный O(N) – метод основан на простом цикле, например
поиск в массиве элемента, подсчет суммы, произведения, поиск
элемента
• Квадратичный О(N**2).
Основан на двойном цикле (внешний и вложенный). Это
‒ поиск элемента в матрице, расчет сумм, произведений в
матрице
‒ сортировка массива
• Полиномиальный (N**М) – это обобщение двух предыдущих.
Чаще основан на М – циклах.
• Логарифмический О(logN) – бинарный поиск (поиск делением
пополам), «угадать число» (да,нет)
• Линейно-логарифмический (N*logN) – сортировка слиянием
15

16.

• Экспоненциальная сложность O(2**N). Экспоненциальные
функции, такие как 2N, возрастают молниеносно и поэтому
полезны для решения ограниченного круга задач.
‒ Обычно посредством алгоритмов с подобным временем
работы ищется оптимальный набор входных данных.
‒
Хорошим примеров может быть задача поиска
оптимального решения, например, составления расписания.
• N! - функция N! (читается как «N факториал»).
‒ Она возрастает намного быстрее, чем экспоненциальная
функция 2N.
‒ В алгоритмах с факториальным временем работы, как
правило, ищется оптимальное распределение входных
данных.
‒ Например, задача о коммивояжере:
имеется список городов. Его задача — составить маршрут
таким образом, чтобы посетить каждый населенный пункт один
раз и вернуться в отправную точку, преодолев минимальное
расстояние.
16

17.

3. Правила оценки асимптотической сложности
17

18.

При оценке асимптотической временной сложности
руководствуются правилами:
1. Если для математической функции f алгоритму необходимо
выполнить определенные действия f(N) раз, то для этого ему
понадобится сделать O(f(N)) шагов.
2. Если алгоритм выполняет одну операцию, состоящую из
O(f(N)) шагов, а затем вторую операцию, включающую O(g(N))
шагов, то общая производительность алгоритма для функций f
и g составит O(f(N) + g(N)).
3. Если алгоритму необходимо сделать O(f(N) + g(N)) шагов и
производительность функции f(N) меньше, чем у g(N), то
асимптотическую сложность можно упростить до выражения
O(f(N)).

19.

4. Если алгоритму внутри каждого шага O(f(N)) одной операции
приходится выполнять еще O(g(N)) шагов другой операции, то
общая производительность алгоритма составит O(f(N) * g(N)).
5. Постоянными множителями (константами) можно пренебречь.
Если C является константой, то O(C * f(N)) или O(f(C * N)) можно
записать как O(f(N)).
19

20.

(Кратко) сводка правил оценки сложности
1) Вынесение константы O(C * f(N)) = C*O(f(N))
2) Последовательность инструкций –
O(f(N)); O( g(N)) = O(f(N) + g(N))
3) Упрощение (для асимптотической оценки)
O(f(N)+g(N)) = Max (O(f(N)), O(g(N))).
4) Вложенность - O(f(N)*g(N)) = O(f)*O(g),
20

21.

4. Несколько примеров
кода и оценок
21

22.

Пример 1. Размер коллекции
def getSize(collection):
return len(collection)
Сложность O(1)
collection=[1,2,3,4,5]
n=getSize(collection)
print(n)
Тестовая часть кода
не входит в оценку
Оценка – O(1) – есть результат.
Здесь, если есть, подготовительные операции, то они
должны быть учтены как некоторая константная оценка C.
Общая асимптотическая оценка – O(1)
22

23.

def getSize(collection):
return len(collection)
Стиль Питон
static int getSize(int[] collection) {
return collection.length;
}
Стиль java
static int getSize(int[] collection)
{
return collection.length;
}
Стиль С#
Как видим, способ описания в Питоне более компактный
23

24.

А если мы введем обобщенный тип в описание
def getSize(collection):
return len(collection)
Стиль Питон
package com.company;
import java.util.ArrayList;
public class Test<T> {
public int getSize(T[] collection) {
return collection.length;
}
Стиль java
public int getSize(ArrayList<T> collection) {
return collection.size();
}
}
Размер описания ЯВНО не пользу java или C#
24

25.

Пример 2. Поиск элемента в коллекции (массиве)
def sequentialSearch(collection, t):
for e in collection:
if e == t:
return True
return False
Оценим его временные характеристики
1. Наилучшая оценка – O(1) – первый же элемент - есть результат
2. Наихудшая оценка – O(N) – искомый элемент в конце
3. Средняя оценка – O(N/2)
Примечание: Здесь подготовительные операции и сравнения также
могут быть учтены как некоторая константная оценка C.
Общая асимптотическая оценка сводится к оценке цикла и равна 2
5
O(N)

26.

Пример 3. Поиск максимума в коллекции (массиве)
def maxSearch(collection):
max=collection[0]
for e in collection:
if max<et:
max=e
return max
Оценим его временные характеристики
1. Наилучшая оценка – O(c1*N), c1 – стоимость шага по циклу и
сравнения
2. Наихудшая оценка – O(c2*N), c2 - стоимость шага по циклу и
сравнения, плюс переприсвоение max, с2=с1+с21. с21 –
стоимость переприсвоения
3. Средняя оценка – O(c3*N), c3=(c1+c2)/2
26

27.

5. Индивидуальные задания
27

28.

Индивидуальные задачи
(на работу с массивами)
1) Разработать и описать алгоритм решения задачи
2) Построить блок-схему и оценить по блок-схеме его
трудоемкость
3) Реализовать алгоритм на Питоне
4) Используя модуль питона time – оценить длительность
реализации для разных значений n – размера массива (вектора)
• N=100
• N=1000
• N=10000
• N=100000
5) Рассчитать асимптотическую оценку.
6) Построить табулированную функцию о визуально пояснить ее
вид и сходство (различие) с асимптотической оценкой
28

29.

Номер варианта и условие задачи
1 Подсчитать количество элементов вектора, по значению принадлежащих интервалу [A,B]
2 Подсчитать количество отрицательных элементов вектора
3 Подсчитать сумму чисел, по значению меньших последнего элемента вектора
4 Подсчитать произведение чисел, по значению больших A
5 Подсчитать среднее арифметическое отрицательных элементов вектора
6 Подсчитать количество элементов вектора, по значению больших A и стоящих на нечетных местах
7 Подсчитать сумму квадратов положительных элементов вектора, стоящих на четных местах
8 Подсчитать количество элементов вектора, больших первого элемента
9 Подсчитать сумму элементов вектора, по значению принадлежащих интервалу [A,B]
10 Подсчитать количество чисел, больших последнего элемента вектора
11 Вычислить произведение положительных элементов вектора
12 Подсчитать сумму элементов вектора, больших A и стоящих на четных местах
13 Подсчитать произведение элементов вектора, меньших A и стоящих на нечетных местах
14 Подсчитать сумму отрицательных и стоящих на четных местах элементов вектора
15 Подсчитать среднее арифметическое положительных элементов вектора
29

30.

Результат жду в следующую среду …
Опоздавшие готовят рефераты …
30

31.

The End
31