Похожие презентации:
Закон Ома. Законы Кирхгофа. Баланс мощностей в электрической цепи
1.
Закон Ома. Законы Кирхгофа.Баланс мощностей в
электрической цепи.
2.
Источники ЭДС или напряжения и тока.Источником напряжения называется такой источник электроэнергии, у
которого внутреннее сопротивление R0 мало (С0 - велика), поэтому
напряжение на его зажимах практически не зависит от тока нагрузки;
у источника тока R0 велико (G0 — мала), поэтому ток нагрузки
практически не зависит от напряжения на его зажимах.
Важнейшей характеристикой источников напряжения и тока
являются внешние характеристики, под которыми понимают: для
источников ЭДС - зависимость напряжения от тока при постоянных ЭДС
и внутреннем сопротивлении, снятые с использованием схемы.
Установим соотношения, описывающие указанные характеристики, и
аппроксимируем (изобразим) их графически.
3.
1. Реальными источниками ЭДС могут быть синхронные генераторы наэлектростанциях или аккумуляторные батареи, используемые во
многих радиоэлектронных устройствах, мобильной технике (самолеты,
автомобили, тракторы и др.). У них внутренние сопротивления малы.
Внешняя характеристика источника ЭДС описывается выражением
, из которого
ростом тока I напряжение U уменьшается линейно.
очевидно,
что
с
Зависимость тока нагрузки от сопротивления описывается формулой
, из которой очевидно, что с ростом
сопротивления R ток I уменьшается по кривой, т.е. при R = 0 (короткое
замыкание источника ЭДС) I = Е / R0 = Iкз, при R =∞(холостой ход источника
ЭДС) I = Е / ∞ = 0 = /хх.
2. Реальным источником тока можно моделировать коллекторную цепь
схемы замещения биполярного транзистора или истоковую —
полевого, а также схемы некоторых классов усилителей.
4.
Закон ОмаЗакон Ома для участка цепи, не содержащего ЭДС, записывается так:
Закон Ома для участка цени с источником ЭДС, выступающим в качестве
источника электроэнергии, например во второй ветви, запишется так
5.
Законы (правила) КирхгофаПервое правило (закон) Кирхгофа гласит: алгебраическая сумма
токов в узле цепи равна нулю, т.е.
где k — число токов ветвей, сходящихся в узле. При этом знаки перед
токами берутся с учетом их произвольно выбранных положительных
направлений: всем
токам, направленным
к узлу,
например,
приписывается знак «+», от узла — «-» или наоборот.
Второе правило Кирхгофа гласит: алгебраическая сумма ЭДС в
любом замкнутом контуре цепи равна алгебраической сумме
напряжений вдоль того же контура, т.е.
6.
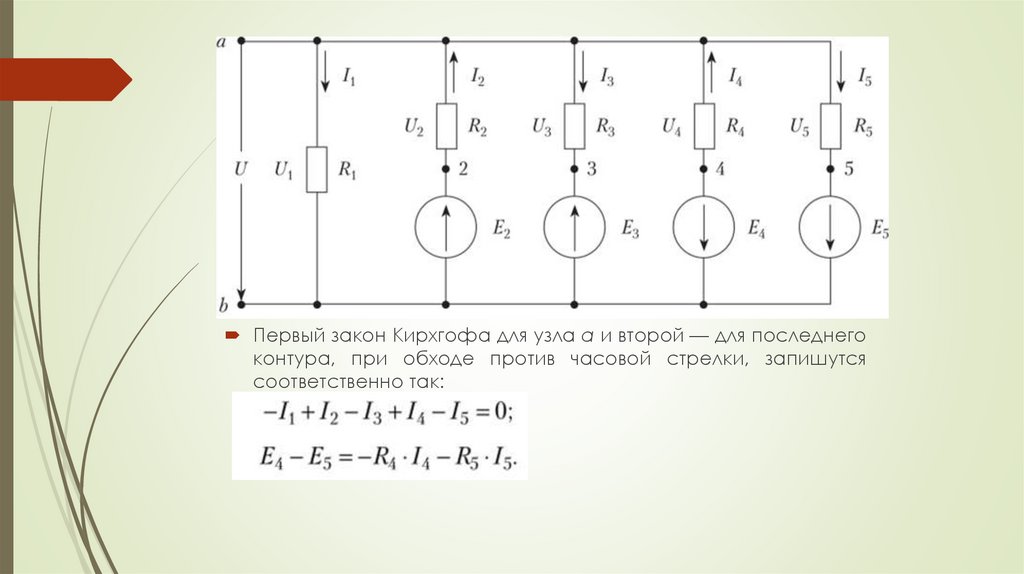
Первый закон Кирхгофа для узла а и второй — для последнегоконтура, при обходе против часовой стрелки, запишутся
соответственно так:
7.
Баланс мощности в электрической цепив любой электрической системе (или цепи) должен соблюдаться закон
сохранения энергии. В приложении к электрическим цепям этот закон
интерпретируется балансом мощности, сущность которого заключается
в том, что сумма мощностей источников питания, участвующих в схеме,
равняется сумме мощностей приемников электроэнергии, т.е.
8.
Расчет цепей с одним источником питанияЦепь с последовательным соединением резисторов.
От идеализированного источника ЭДС Е (R0 = 0), на выходных зажимах которого
имеется напряжение U, т.е. когда Е = U, через последовательно соединенные
сопротивления R1, R2,..., Rn питается нагрузка (приемник) с сопротивлением RH
Задача. Чему равны сопротивление, напряжение и мощность цепи по рис. а, если I =
1 A, R1 = 1 Ом, R2 = 2 Ом, R3 = 3 Ом, Rн = 4 Ом?
9.
Цепь с параллельным соединениемрезисторов.
От источника ЭДС Е, на выходных зажимах которого имеется напряжение
U, через параллельно соединенные сопротивления R1, R2, ..., Rn питается
нагрузка с сопротивлением Rн
Задача. В цепи на рис. а известны: U=110 В, R1=1 Ом, R2=2 Ом, R3=3 Ом, RH=4 Ом.
Определить Р , токи в ветвях
10.
Цепи со смешанным соединением резисторов.Разветвленные схемы, где наряду с последовательными участками имеются
параллельные, относятся к схемам со смешанным соединением сопротивлений.
Они приводятся к схемам с одним эквивалентным сопротивлением путем
постепенного объединения сопротивлений цепи, начав с ее конца.
1. Применительно к схеме по рис., а такое объединение или свертка реализуется
в следующей последовательности.
А. Сначала объединяются ветви 3 и 2. Поскольку они
соединены параллельно, то
Б. Затем объединяются участки 3—2 и 1. Поскольку
они соединены последовательно, то
Полученное сопротивление R и будет общим для всей цепи по рис. 2.3, а. С учетом
этого определяют: токи
11.
Конденсаторы в цени постоянного токаПри установившемся режиме работы цени постоянного тока, когда по истечении
определенного времени после подключения ее к источнику питания в ней
устанавливаются неизменные токи, напряжения, ЭДС, конденсаторы, как
указывалось раньше, являются местами разрыва цепи, поэтому они не проводят
ток, т.е. I = 0. В такой ситуации конденсаторы находятся в заряженных состояниях и
являются
временными
накопителями
электроэнергии,
определяемой
выражением Э = 0,5CU2. Это свойство конденсаторов используется для
организации памяти в компьютерах, а также таймерах, часах, в электрических
фильтрах, искрогасителях в коммутационных аппаратах и др.
Между тем при использовании конденсаторов в цепях постоянного тока в
качестве электрических фильтров возникают чисто практические задачи.
Например,
когда
номинальные
значения
емкости
или
напряжения
конденсаторов, имеющихся в наличии, не совпадают с расчетными, их
соединяют в батареи, т.е. последовательно, параллельно, смешанно.
Рассмотрим их особенности.
12.
А. При последовательном соединении конденсаторов (рис. а), в соответствии совторым правилом Кирхгофа, общее напряжение на зажимах всей цепи равно сумме
напряжений на отдельных конденсаторах (элементах цепи), т.е.
Б. При параллельном соединении конденсаторов (рис. б) общий заряд q, накопленный
в конденсаторах, равен сумме зарядов на отдельных конденсаторах, т.е.
В. При смешанном соединении конденсаторов общая емкость
постепенным преобразованием схемы. Например, для цепи по рис. в:
С= ((С2+ С3)С1) /(C1+С2+С3).
находится
13.
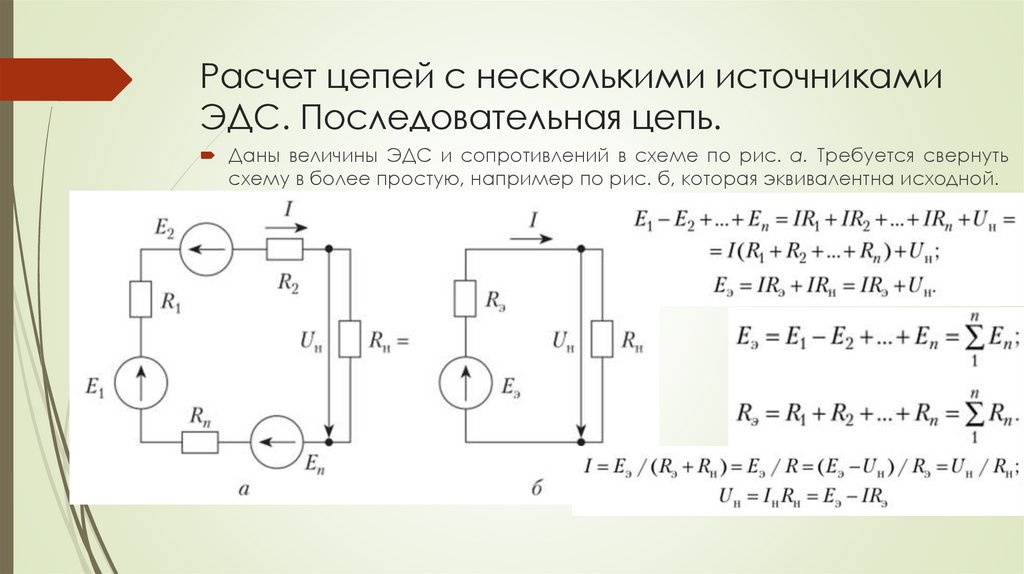
Расчет цепей с несколькими источникамиЭДС. Последовательная цепь.
Даны величины ЭДС и сопротивлений в схеме по рис. а. Требуется свернуть
схему в более простую, например по рис. б, которая эквивалентна исходной.
14.
Параллельная цепь.Даны величины ЭДС и сопротивлений параллельной цепи по рис. а.
Требуется свернуть исходную схему в простейшую по рис. б.
15.
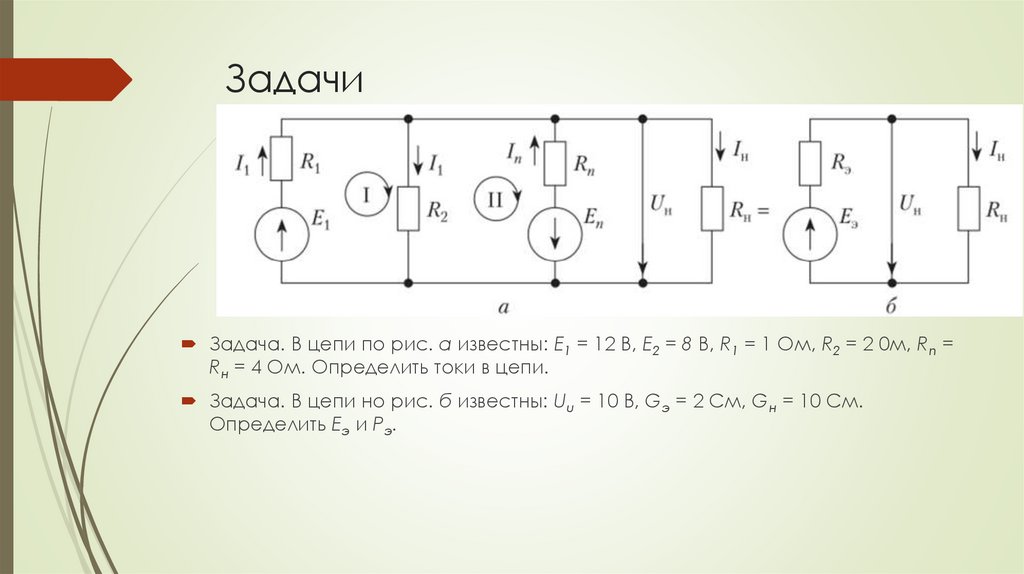
ЗадачиЗадача. В цепи по рис. а известны: Е1 = 12 В, Е2 = 8 В, R1 = 1 Ом, R2 = 2 0м, Rn =
Rн = 4 Ом. Определить токи в цепи.
Задача. В цепи но рис. б известны: Uu = 10 В, Gэ = 2 См, Gн = 10 См.
Определить Еэ и Рэ.
16.
Метод с непосредственнымприменением законов Кирхгофа
Последовательность расчета этим методом:
1) произвольно задают направления токов в ветвях цепи;
2) произвольно задают направления обхода независимых контуров цепи;
3) по первому закону Кирхгофа составляется столько уравнений, сколько
узлов в схеме (n) без единицы, т.е. (n - 1);
4) по второму закону Кирхгофа составляется столько уравнений, сколько
искомых величин (t) за вычетом числа уравнений, составленных но первому
закону Кирхгофа, т.е. t -(n - 1);
5) совместное решение полученных уравнений дает ответ задачи. При этом
отрицательный ответ для какого-либо тока указывает на то, что его
направление обратно произвольно выбранному.
17.
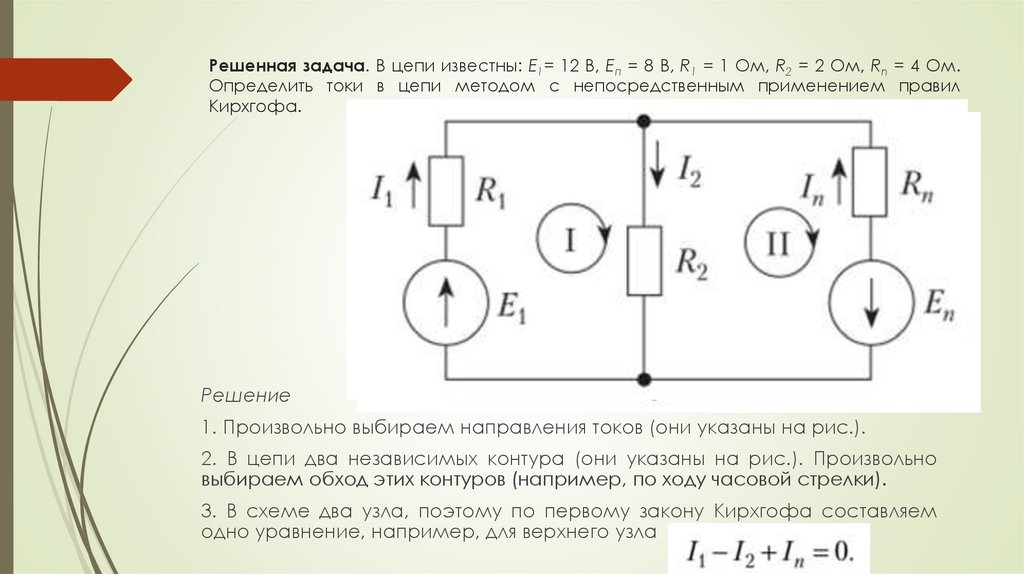
Решенная задача. В цепи известны: Е1= 12 В, Еп = 8 В, R1 = 1 Ом, R2 = 2 Ом, Rn = 4 Ом.Определить токи в цепи методом с непосредственным применением правил
Кирхгофа.
Решение
1. Произвольно выбираем направления токов (они указаны на рис.).
2. В цепи два независимых контура (они указаны на рис.). Произвольно
выбираем обход этих контуров (например, по ходу часовой стрелки).
3. В схеме два узла, поэтому по первому закону Кирхгофа составляем
одно уравнение, например, для верхнего узла
18.
4. В схеме три искомых тока, для которых уже составлено одно уравнение.Поэтому по второму закону Кирхгофа составляем два уравнения для
независимых контуров:
5. Решим совместно полученные уравнения. Для этого перепишем их,
подставив в последних двух известные значения электрических величин:
Решив уравнения методом подстановки, получим:
Последнее означает, что 1п в схеме реально направлен вниз.
Правильность решения задачи проверяем по первому правилу Кирхгофа,
т.е. 6,3 - 2,9 - 3,4 = 0.
В общем случае, когда уравнений много, их решают совместно методами
определителей или матриц.
19.
Метод контурных токовМетод основан на определении действительных (реальных) токов в цепи по так
называемым контурным токам, являющимся фиктивными (расчетными) и
считающимся замыкающимися по независимым контурам. Метод контурных токов,
по сравнению с предыдущим, позволяет сократить число совместно решаемых
уравнений до t-n, поскольку они составляются по второму правилу Кирхгофа лишь
для независимых контуров.
Последовательность расчета этим методом:
1) задают произвольно направления контурных токов в независимых контурах;
2) составляют уравнения по второму закону Кирхгофа для независимых контуров, по
которым замыкаются контурные токи;
3) совместным решением этих уравнений определяют контурные токи;
4) по контурным токам находят действительные токи. При этом:
а) контурные токи равны действительным в тех ветвях, где протекают лишь они
одни,
б) действительные токи равны алгебраическим суммам контурных токов в тех
ветвях, где протекают по несколько контурных токов.
20.
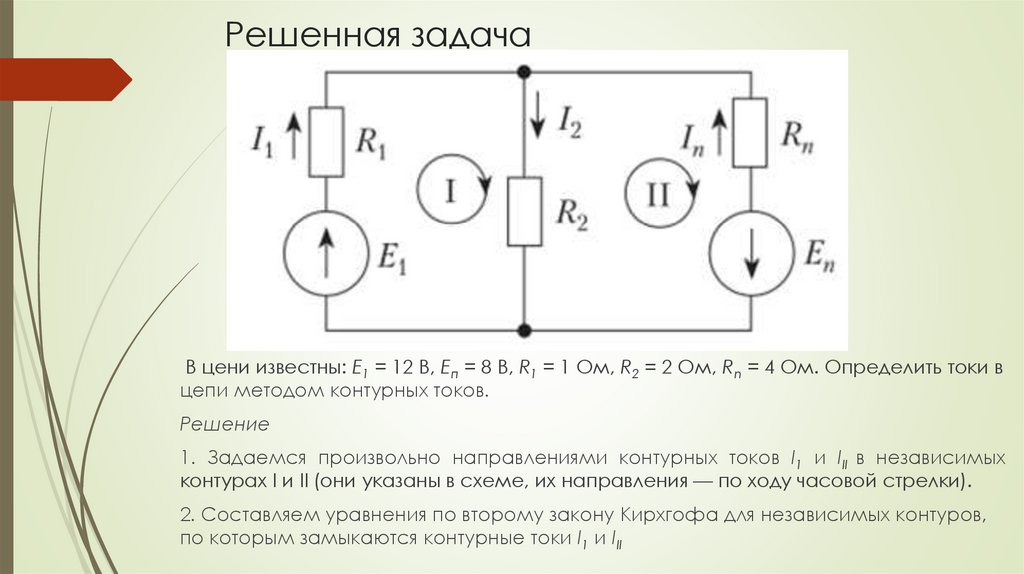
Решенная задачаВ цени известны: Е1 = 12 В, Еп = 8 В, R1 = 1 Ом, R2 = 2 Ом, Rn = 4 Ом. Определить токи в
цепи методом контурных токов.
Решение
1. Задаемся произвольно направлениями контурных токов I1 и III в независимых
контурах I и II (они указаны в схеме, их направления — по ходу часовой стрелки).
2. Составляем уравнения по второму закону Кирхгофа для независимых контуров,
по которым замыкаются контурные токи I1 и III
21.
Решив совместно эти уравнения, получаем: II ~ 6,3 А и III ~ 3,4 А.По контурным токам находим реальные токи:
Полученные значения токов совпадают с теми, что получены в предыдущей
задаче, т.е. она решена верно.
22.
Метод наложенияЭтот метод основан на принципе наложения, который формулируется так: ток в
какой-либо ветви сколь угодно сложной схемы равен алгебраической сумме
токов, вызываемых в этой ветви каждым источником ЭДС в отдельности. Метод
наложения позволяет свести расчет разветвленной цепи с несколькими ЭДС к
расчетам нескольких цепей, в которых присутствуют по одной ЭДС.
Последовательность расчета этим методом такова:
1) исходную схему с несколькими ЭДС расчленяют на несколько частичных
схем, в которых присутствуют по одной ЭДС и все сопротивления, в том числе
внутренние удаленных ЭДС;
2) намечают направления частичных токов в полученных схемах так, как они
вызываются ЭДС, а не произвольно;
3) поочередно рассчитывают частичные токи в частичных схемах;
4) реальные токи находят путем алгебраического сложения (наложения)
частичных токов соответствующих ветвей.
23.
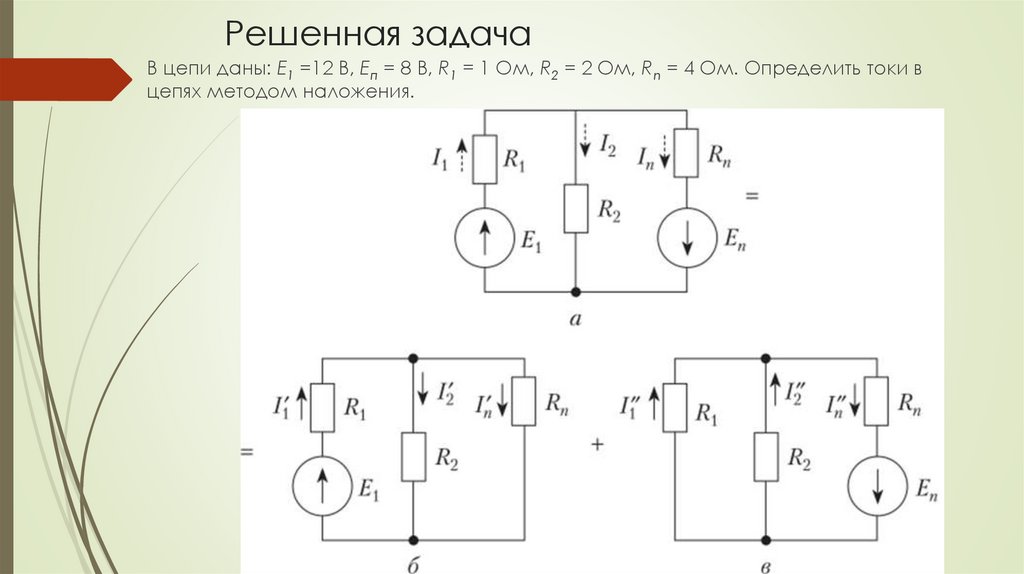
Решенная задачаВ цепи даны: Е1 =12 В, Еп = 8 В, R1 = 1 Ом, R2 = 2 Ом, Rn = 4 Ом. Определить токи в
цепях методом наложения.
24.
Решение1. Расчленяем схему по рис. а на две частичные схемы б и в, в которых
оставлены по ЭДС и все сопротивления исходной схемы, в том числе
внутренние сопротивления удаленных ЭДС.
2. Намечаем в частичных схемах направления частичных токов так, как они
вызываются ЭДС (указаны на рис. б и в).
3. Рассчитываем частичные токи схемы б: I′ I = Е1/ [R1 + R2Rn/(R2 +Rn )] = 12 / [1 + 2
•4 /(2 + 4)] =5,14 A; I′2 = I′ I Rn/(R2 + Rn) = 5,14 • 4/(2 + 4) ~ 3,4 A; I′ n=I′ I -I′ 2 = 5 - 3,4 =
1,6 А. Рассчитываем частичные токи схемы в: I″n = E2/[Rn + R1R2/(R1+R2)] = 8/[4+1•2
/(1+2)] = 1,7А; I″2 = I″ n R1/(R1+R2) = 1,7 •1/(2+1) = 0,6А; I″ 1=I″ n -I″2=1,7-0,6=1,1 А
4. Находим реальные токи путем наложения частичных токов схем: II = I′ I + I″ 1=
= 5,14+1,1 =6,14 А, I2 = I′2 - I″2 =3,4 -0,6 = 2,8А, I n = I′ n +I″ n = 1,6 + 1,7 =3,3 А. На рис.
а показаны пунктиром направления реальных токов.
Полученные значения токов I1,I2, In отличаются от аналогичных предыдущих: I1 на
0,06 А, что составляет 2,5%, I2 на 0,1 А (3,4%) In на 0,1 А (3%). При инженерных
расчетах ошибка может составлять до 10%. Поэтому будем считать, что задача
решена правильно.
25.
Метод узлового напряжения (метод двух узлов)В цепи, имеющей два узла (или легко сводящейся к ней), токи в ветвях рационально
определять методом узлового напряжения или двух узлов, сущность которого заключается в
нахождении узлового напряжения и последующем определении искомых токов по закону
Ома. Метод узлового напряжения является частным случаем более универсального метода
— метода узловых потенциалов, который будет рассмотрен ниже.
Последовательность расчета токов методом двух узлов такова:
1) произвольно выбирают направление узлового напряжения. При этом целесо-образно его
выбирать противоположным большинству направлений ЭДС в ветвях;
2) намечают на схеме направления токов в ветвях по правилу: в пассивных ветвях — по
направлению узлового напряжения, в активных — произвольно;
3) определяют узловое напряжение
- алгебраическая сумма произведений ЭДС на проводимости k ветвей, где
включены источники ЭДС;
- арифметическая сумма проводимостей всех
параллельных ветвей m; Gн — проводимость нагрузки, параллельной остальным ветвям.
Узловое напряжение равно отношению алгебраической суммы произведений ЭДС
каждой ветви на их проводимости к общей проводимости всех ветвей схемы, найденной
путем арифметического сложения последних. При этом произведения ЭДС и
проводимостей берутся со знаком «+», если направления ЭДС и узлового напряжения не
совпадают, и со знаком «-» — если совпадают.
4) используя узловое напряжение Uy3, определяют искомые токи но закону Ома.
26.
Решенная задачаВ цепи даны: Е1 =12 В, Еп = 8 В, R1 = 1 Ом, R2 = 2 Ом, Rn = 4 Ом. Определить токи в цени
методом наложения.
Решение
1. Выбираем направление узлового напряжения Uy3 = UH относительно схемы сверху
вниз.
2. Определяем узловое напряжение:
Если считать, что нагрузка отсутствует, тогда расчет сведется к предшествующим
настоящей задачам. В самом деле:
Из этого очевидно, что узловое напряжение Uy3 оказалось равным эквивалентной
ЭДС Еэ, о чем говорилось выше.




















 Физика
Физика








