Похожие презентации:
Сила Лоренца
1.
Сила Лоренца2.
2(1853 – 1928 г.г.)
великий
нидерландский
физик – теоретик,
создатель
классической
электронной
теории
Лоренц Хендрик Антон
Лоренц ввел в электродинамику представления о
дискретности электрических зарядов и записал
уравнения для электромагнитного поля, созданного
отдельными заряженными частицами (уравнения
Максвелла – Лоренца); ввел выражение для силы,
действующей на движущийся заряд в электромагнитном
поле; создал классическую теорию дисперсии света и
объяснил расщепление спектральных линий в
магнитном поле (эффект Зеемана). Его работы по
электродинамике движущихся сред послужили основой
для создания специальной теории относительности.
3.
3Сила Лоренца -
это сила, с которой магнитное поле действует на
заряженные частицы
4.
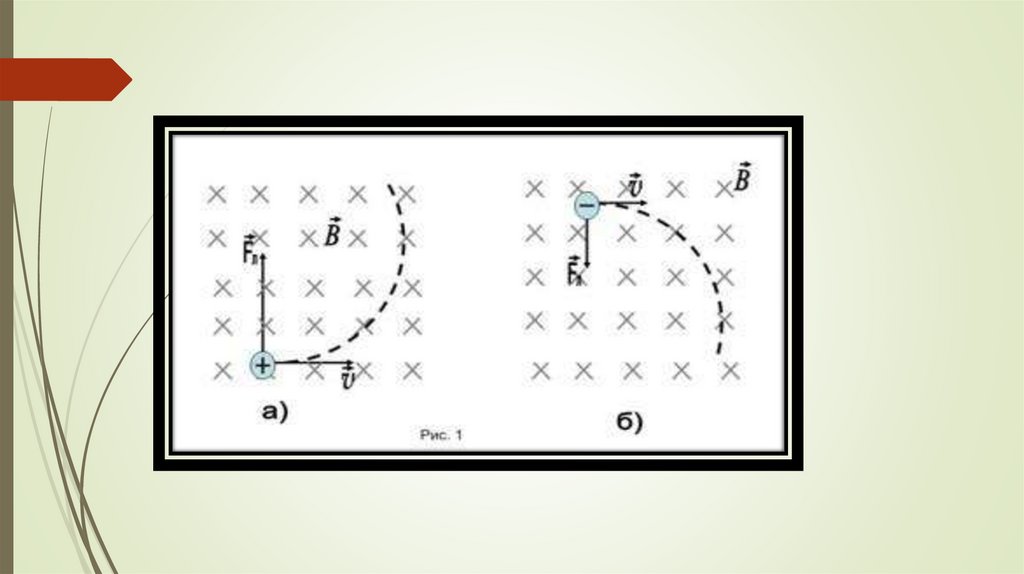
Направление силы ЛоренцаПравило левой руки
Если поставить левую руку так,
чтобы перпендикулярная скорости
составляющая вектора индукции
входила в ладонь, а четыре
пальца были бы расположены по
направлению скорости движения
положительного заряда (или
против направления скорости
отрицательного заряда), то
отогнутый большой палец укажет
направление силы Лоренца.
5.
Применяя правило левой руки, нужнопомнить, что если в магнитном поле
движется положительный заряд то
четыре вытянутых пальца должны быть
направлены в сторону его движения, т.
е. в сторону вектора а если движется
отрицательный заряд то вытянутые
четыре пальца должны быть направлены
против
6.
Сила Лоренца перпендикулярнаскорости и поэтому она не совершает
работы, не изменяет модуль скорости
заряда и его кинетической энергии. Но
направление скорости изменяется
непрерывно
7.
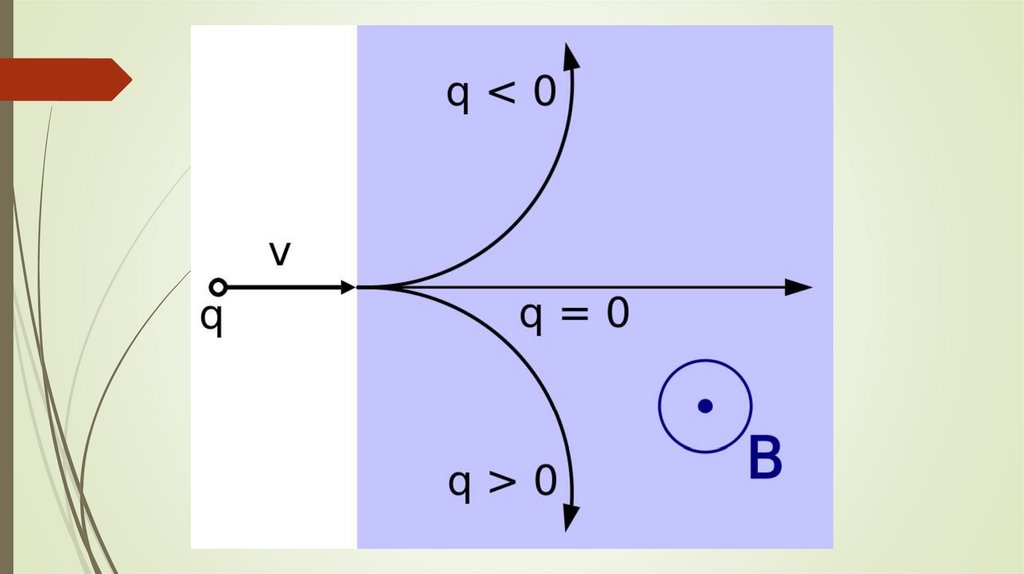
Пространственные траектории заряженных частиц в7
магнитном
поле
Частица влетает в магнитное поле ll линиям
магнитной индукции => α = 0˚ => sin α = 0
=>
Fл = 0
Если сила, действующая на частицу = 0, то частица, влетающая в
магнитное поле, будет двигаться
равномерно и прямолинейно вдоль линий
магнитной индукции
8.
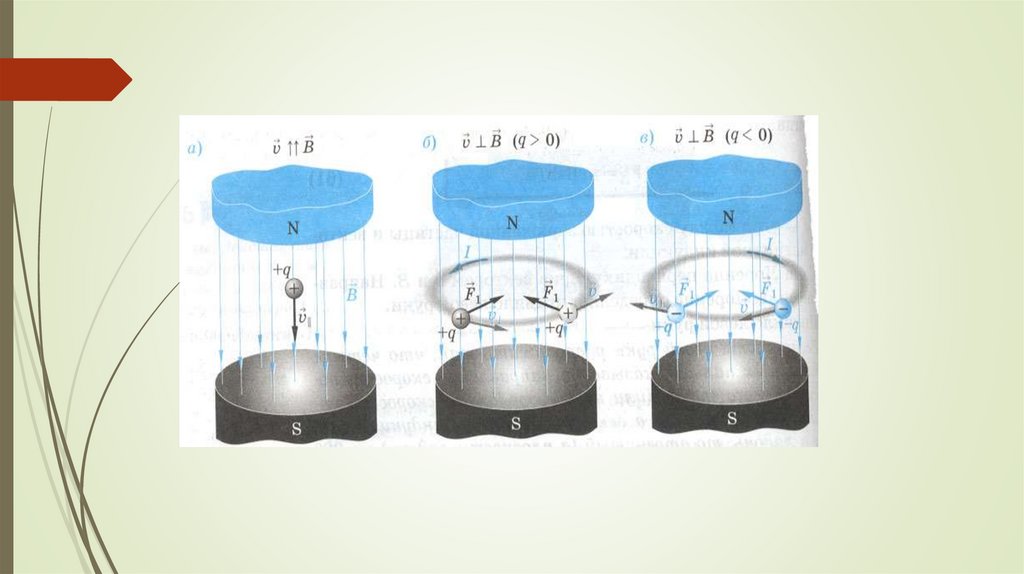
Пространственные траектории заряженных частиц в8
магнитном
поле
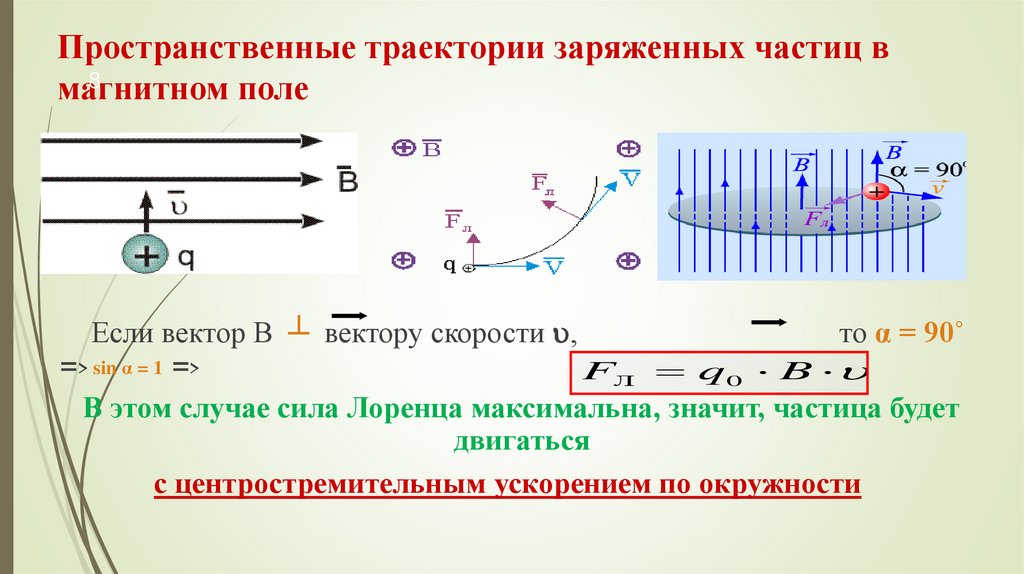
Если вектор В ┴ вектору скорости ,
то α = 90˚
=> sin α = 1 =>
FЛ q 0 B Sin
В этом случае сила Лоренца максимальна, значит, частица будет
двигаться
с центростремительным ускорением по окружности
9.
10.
Пространственные траектории заряженных частиц10
в магнитном поле
1
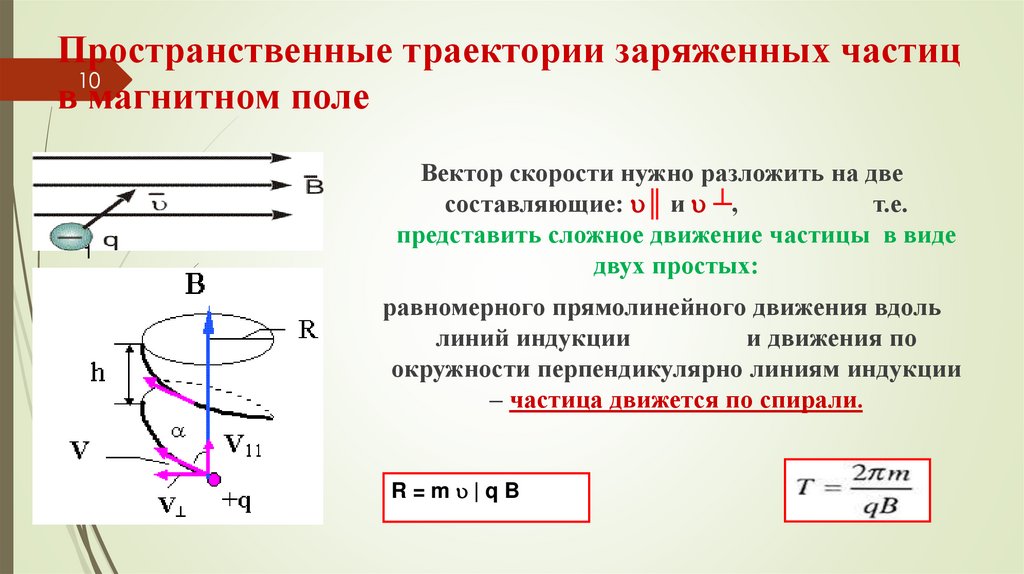
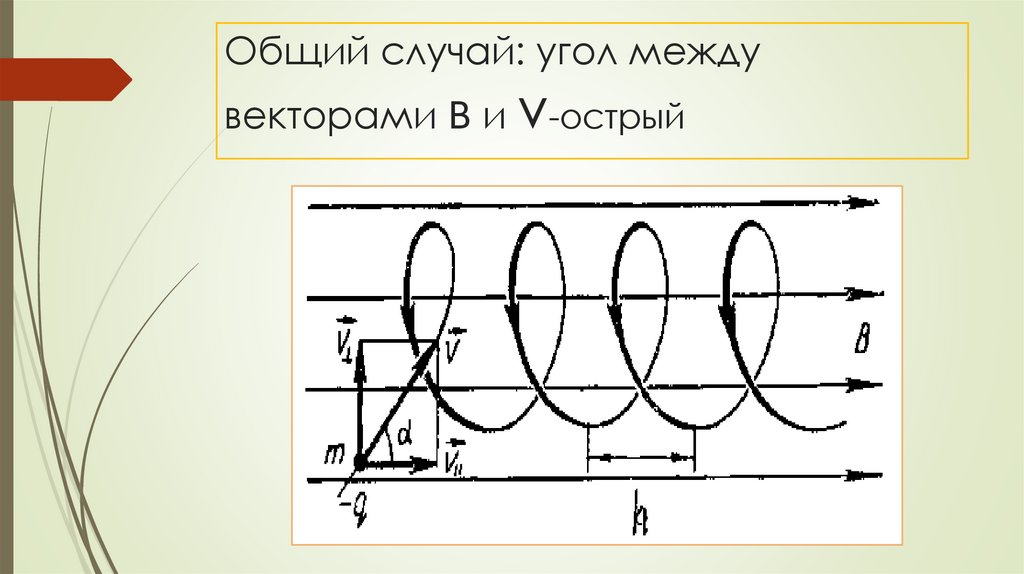
Вектор скорости нужно разложить на две
составляющие: ║ и ┴,
т.е.
представить сложное движение частицы в виде
двух простых:
равномерного прямолинейного движения вдоль
линий индукции
и движения по
окружности перпендикулярно линиям индукции
– частица движется по спирали.
R=m |qB
11.
12.
13.
14.
Общий случай: угол междувекторами в и v-острый
15.
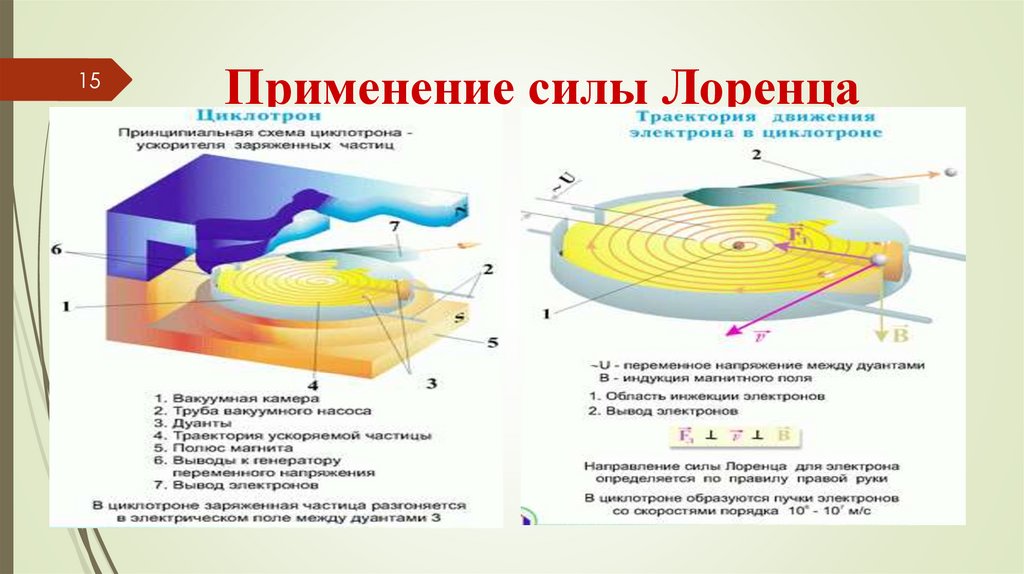
15Применение силы Лоренца







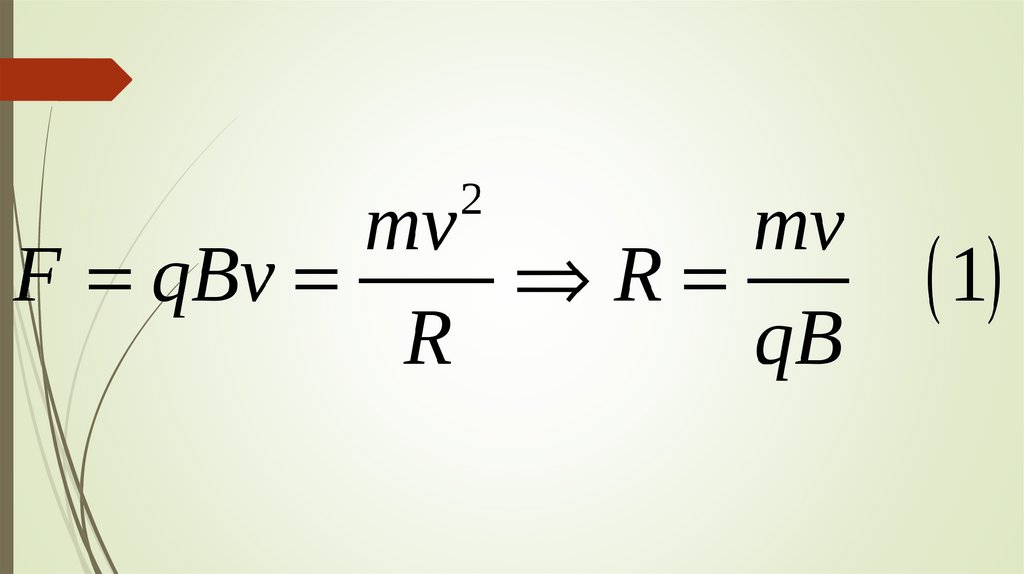
 Физика
Физика








