Таблицы. Распределения. Полигоны частот и центральные тенденции

1.

Полигоны частот и
9 класс

2.

• Понятия , которые мы
будем сегодня
рассматривать
используются в статистике.

3.

• Статистика – это вид практической
деятельности, направленной на собирание,
обработку, анализ и публикацию
статистических данных, характеризующих
количественные закономерности жизни
общества во всем ее многообразии
(экономика, культура, мораль, политика и т.д.).

4.

Этапы статистического исследования
Статистические наблюдения(сбор информации)
Разбивают на группы по какому либо признаку
сводят в таблицы (частот, относительных частот и
интервальные)
Наглядное представление, собранных данных
(диаграммы, гистограммы и полигон)
Вывод (анализ данных)

5.

РАССМОТРИМ ЗАДАЧУ.
• Измерили размер обуви мальчиков одной школы .Были получены
следующие результаты:
38, 42, 39, 40, 40, 40, 44, 41, 41, 44,
41, 41, 41, 41, 40, 41, 42, 42, 44, 44,
42, 42, 39, 42, 43, 43, 43, 43, 38,
44, 44, 40, 45 .

6.

ТАБЛИЦА РАСПРЕДЕЛЕНИЯ ПО
ЧАСТОТАМ
• Пусть случайная величина X – размер обуви мальчиков 9 классов одной
школы.
• М-частота появления определенного размера
X
38
39
40
41
42
43
44
45
M
2
2
5
7
6
4
6
1

7.

РАНЖИРОВАННЫЙ РЯД
38,38,39, 39, 40, 40, 40, 40, 40, 41, 41, 41, 41, 41, 41, 41, 42, 42,
42, 42, 42, 42, 43, 43, 43, 43,
44, 44, 44, 44, 44, 44,45 .
Это упорядоченный ряд исследования
X
M
38
2
39
2
40
5
41
7
42
6
43
4
44
6
45
1

8.

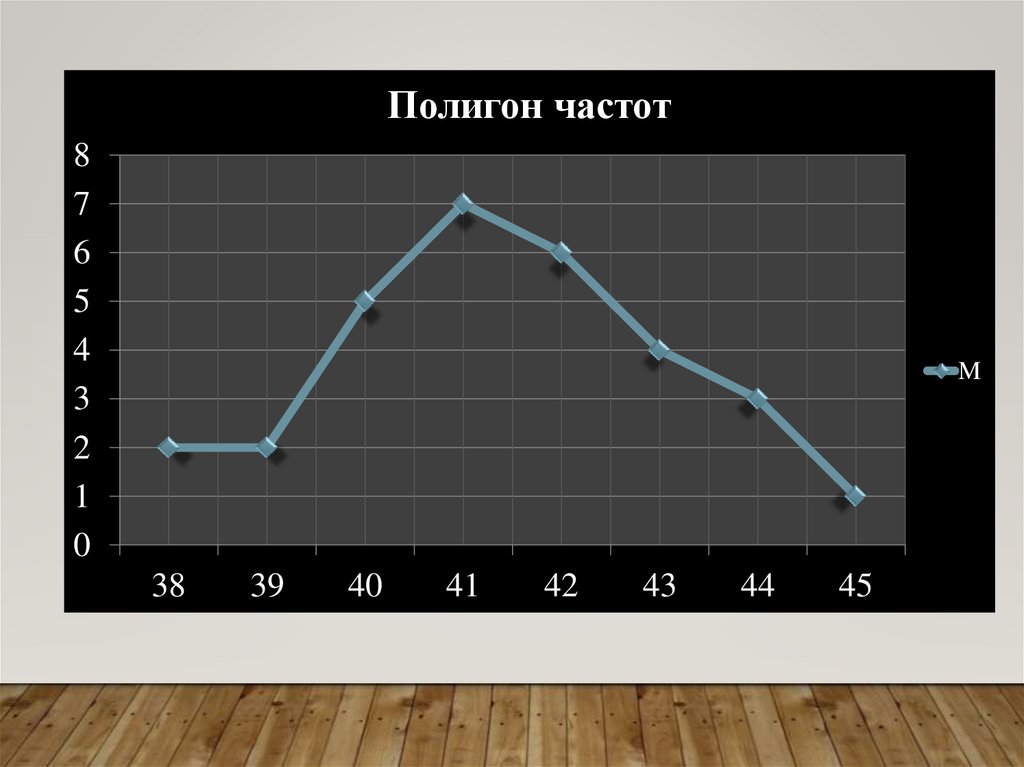
Один из способов графического представления плотности
вероятности случайной величины-Полиго́н часто́т
• Полигон частот –
линейная диаграмма , на которой на горизонтальной оси
откладывают различные значения случайной величины
Х, а по вертикали – их абсолютная или относительная
частота.
Относительная частота = (Частота / Сумму частот)*100%

9.

Полигон частот
8
7
6
5
4
3
2
1
0
M
38
39
40
41
42
43
44
45

10.

ЦЕНТРАЛЬНЫЕ ТЕНДЕНЦИИ
Мода , медиана , и среднее значение
Мода (обозначим Мо) — наиболее часто
встречающееся значение ряда чисел
Медиана (обозначим Me) — это серединное значение
упорядоченного ряда чисел, если в ряду нечетное
число чисел. Если четное число, то среднее
арифметические двух чисел посередине
упорядоченного ряда чисел.

11.

РАССМОТРИМ НА НАШЕМ ПРИМЕРЕ
• МОДА Мо=41, встречается самое большое число раз
• Медиана Ме=42 , так как число 42 находится ровно
посередине ряда.
38, 38, 39, 39, 40, 40, 40, 40, 40, 41, 41, 41,
41, 41, 41, 41, 42, 42, 42, 42, 42, 42, 43, 43,
43, 43, 44, 44, 44, 44, 44, 44,45 .

12.

ПРИМЕР
• Если в упорядоченном ряду четное число чисел, то по
середине два числа. Тогда, чтобы найти медиану, надо
сложить эти два числа и разделить на два.
• Например:
2,3,3,5,6,8.
Ме= (3+5): 2=4- медиана

13.

• Средним значением случайной величины X
(обозначается X ) называют среднее арифметическое
всех её значений.
3,4,1,2,5.
Записываем упорядоченный ряд: 1,2,3,4,5
X
=(1+2+3+4+5):5=15:5=3

14.

• Размах (обозначается R) — разница между
наибольшим и наименьшим значениями случайной
величины.
1,2,3,4,5
R= 5-1=4
• Размах характеризует границы разброса выборки

15.

ПРИМЕР
• Вычислить размах, моду и медиану для
последовательности:
-2, 3, 4, -3, 0, 1, 3, -2, -1, 2, -2, 1.

16.

ПРИМЕР
• Вычислить размах, моду и медиану для
последовательности:
-2, 3, 4, -3, 0, 1, 3, -2, -1, 2, -2, 1.
• ОБЯЗАТЕЛЬНО!
Записываем упорядоченный ряд.
-3,-2,-2,-2, -1, 0, 1, 1, 2, 3, 3, 4

17.

• -3,-2,-2,-2, -1, 0, 1, 1, 2, 3, 3, 4
• Ме=
• Мо=
• R=

18.

• -3,-2,-2,-2, -1, 0, 1, 1, 2, 3, 3, 4
• Ме=( 0+1):2=0,5
• Мо=-2
• R=4-(-3)=7

19.

Меры центральной
тенденции
Мода
Медиана
Среднее
значение
Подчёркнем, что существует возможность измерить, охарактеризовать
совокупность одним числом, к которому стремятся все её значения.
Не для каждой совокупности имеет смысл формально находить
центральные тенденции.