Применение производной для исследования функций на монотонность и экстремумы

1. ТЕМА: ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ ДЛЯ ИССЛЕДОВАНИЯ ФУНКЦИЙ НА МОНОТОННОСТЬ И ЭКСТРЕМУМЫ

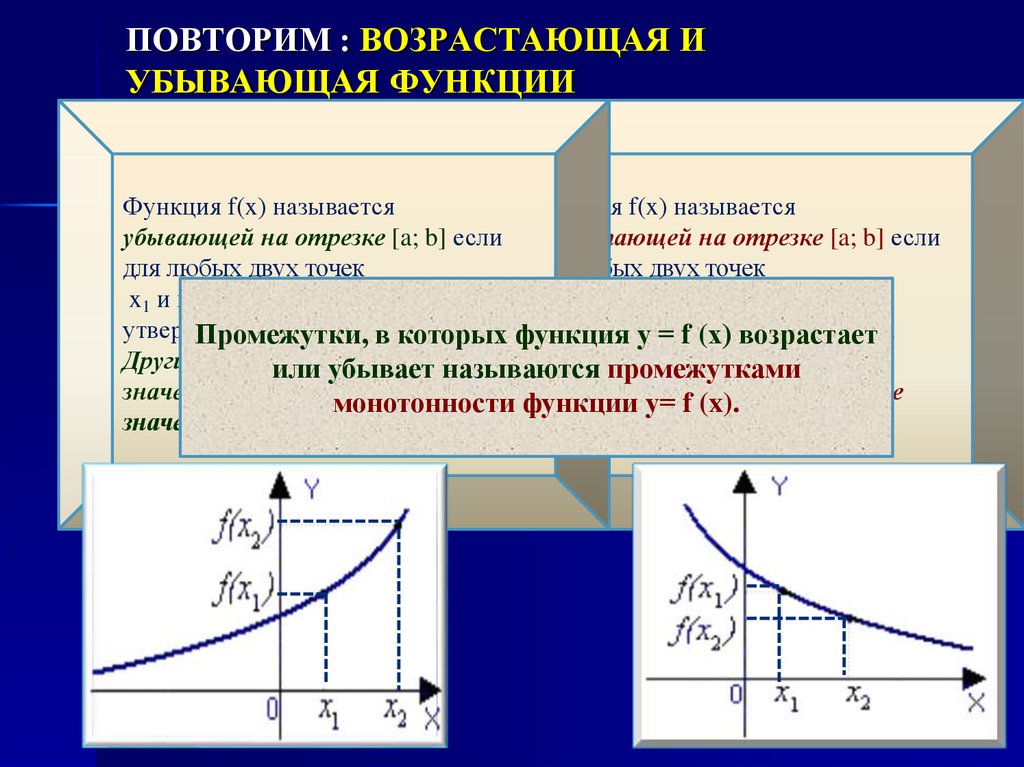
2. ПОВТОРИМ : ВОЗРАСТАЮЩАЯ И УБЫВАЮЩАЯ ФУНКЦИИ

Функция f(x) называется
Функция f(x) называется
убывающей на отрезке [a; b] если возрастающей на отрезке [a; b] если
для любых двух точек
для любых двух точек
x1 и x2 из этого отрезка верно
x1 и x2 из этого отрезка верно
утверждение:
x1 < x2 , f(x
утверждение:
< xвозрастает
1)> f(x2). функция
2 , f(x1)< f(x2).
Промежутки,
в которых
у = xf1(х)
Другими словами,
чем больше
Другими
словами, чем больше
или убывает
называются
промежутками
значение аргумента,
тем меньше функции
значение аргумента,
монотонности
у= f (x). тем больше
значение функции.
значение функции.

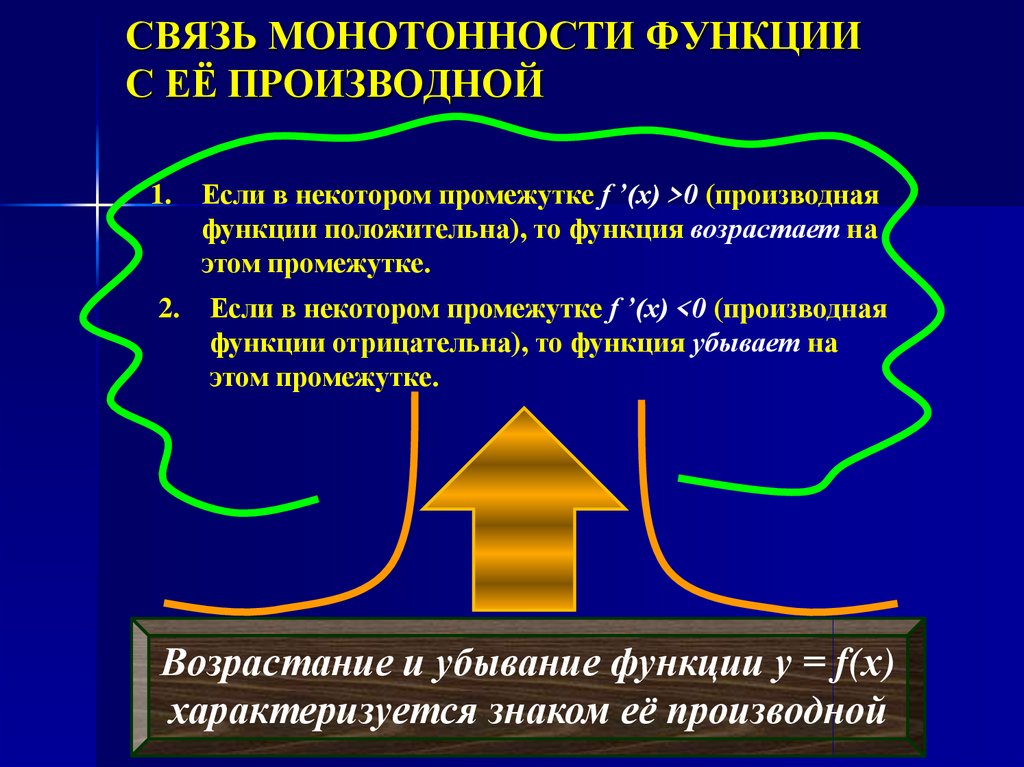
3. СВЯЗЬ МОНОТОННОСТИ ФУНКЦИИ С ЕЁ ПРОИЗВОДНОЙ

1.
Если в некотором промежутке f ’(x) >0 (производная
функции положительна), то функция возрастает на
этом промежутке.
2.
Если в некотором промежутке f ’(x) <0 (производная
функции отрицательна), то функция убывает на
этом промежутке.
Возрастание и убывание функции у = f(х)
характеризуется знаком её производной

4. АЛГОРИТМ ИССЛЕДОВАНИЯ ФУНКЦИИ НА МОНОТОННОСТЬ ПО ГРАФИКУ ПРОИЗВОДНОЙ ФУНКЦИИ

1
Найти область определения функции и интервалы,
на которых функция непрерывна.
2
Найти нули производной, т.е. точки в которых f '(x) = 0.
3
Определить знак производной f '(x) на каждом промежутке.
4
Определить промежутки монотонности.
4.1. Если f ’(x) > 0, то функция возрастает на данном
промежутке.
4.2. Если f ’(x) < 0, то функция убывает на данном
промежутке.

5.

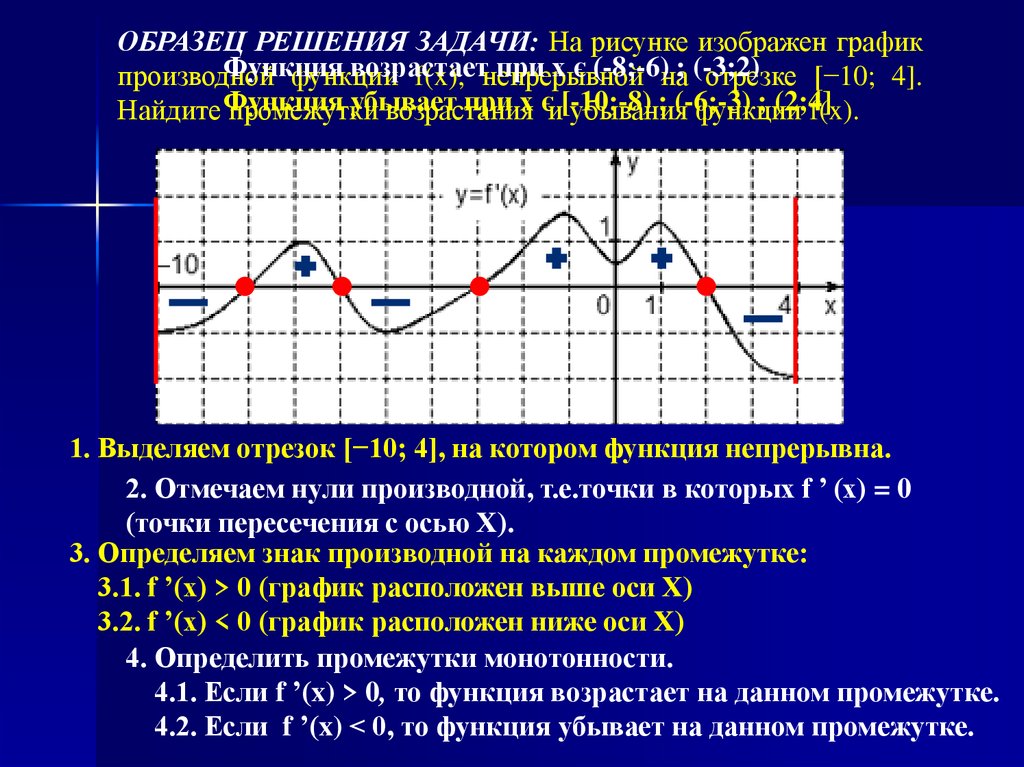
ОБРАЗЕЦ РЕШЕНИЯ ЗАДАЧИ: На рисунке изображен график
Функция
возрастает
при х є (-8;-6)на; (-3;2)
производной
функции
f(x), непрерывной
отрезке [−10; 4].
убывает
при х єи[-10;-8)
; (-6;-3)
; (2;4]
Найдите Функция
промежутки
возрастания
убывания
функции
f(x).
1. Выделяем отрезок [−10; 4], на котором функция непрерывна.
2. Отмечаем нули производной, т.е.точки в которых f ’ (x) = 0
(точки пересечения с осью Х).
3. Определяем знак производной на каждом промежутке:
3.1. f ’(x) > 0 (график расположен выше оси Х)
3.2. f ’(x) < 0 (график расположен ниже оси Х)
4. Определить промежутки монотонности.
4.1. Если f ’(x) > 0, то функция возрастает на данном промежутке.
4.2. Если f ’(x) < 0, то функция убывает на данном промежутке.

6.

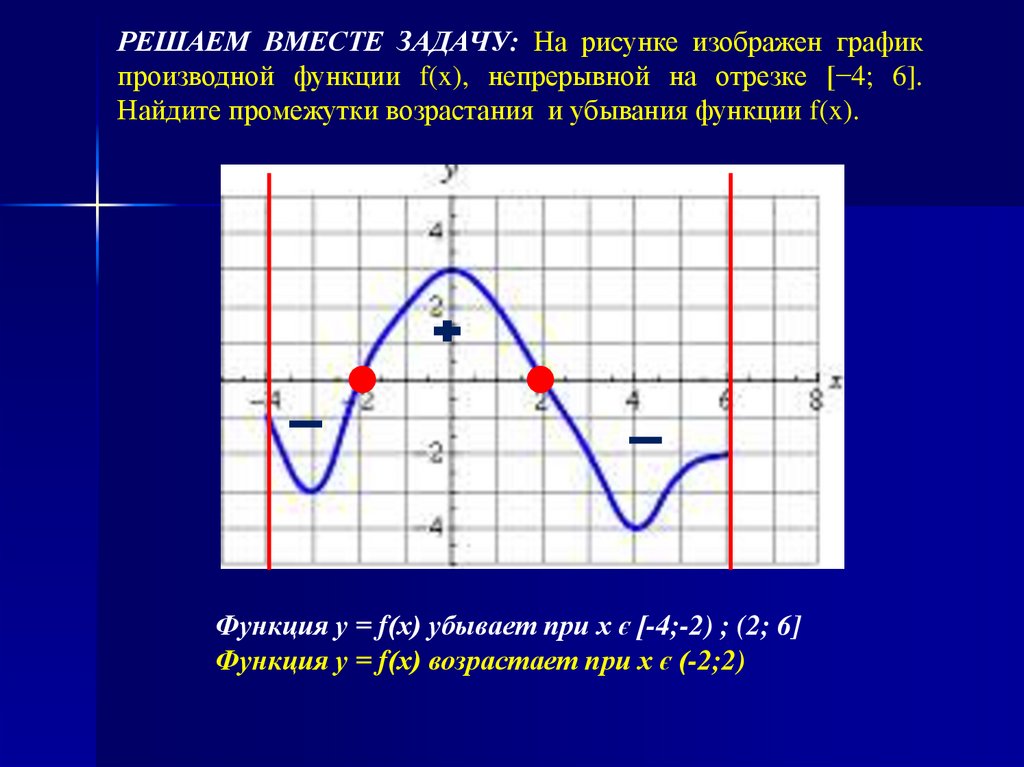
РЕШАЕМ ВМЕСТЕ ЗАДАЧУ: На рисунке изображен график
производной функции f(x), непрерывной на отрезке [−4; 6].
Найдите промежутки возрастания и убывания функции f(x).
Функция у = f(х) убывает при х є [-4;-2) ; (2; 6]
Функция у = f(х) возрастает при х є (-2;2)

7.

ТОЧКИ ЭКСТРЕМУМА ФУНКЦИИ
Точки минимума и максимума
функции называются точками
Точка x0 из области
Точкаа x0 из области
экстремума данной функции,
определения функциизначения
f(x)
функции f(x)
функции определения
в этих
называется точкой
называется точкой
точках экстремумами функции.
максимума
минимума
этой функции , если
этой функции , если
в некоторой окрестности
в некоторой окрестности
этой точки
этой точки выполняется
выполняется неравенство:
неравенство:
f(x0) > f(x).
f(x0) < f(x).

8.

Необходимое условие экстремума
(теорема Ферма): если точка х0 является точкой
Точками
экстремума
служить
экстремума
функции
f (х), имогут
в этой
точке существует
только критические
т.е.точки,
производная
f ’(x), то онаточки,
равна нулю:
f ’(x) =0 .
принадлежащие области определения
функции, вусловие
которыхэкстремума:
производная
Достаточное
обращается в нуль или не существует.
если в некоторой точке х0 производная функции f ( х)
обращается в нуль и, кроме того, проходя через нее слева
направо, меняет свой знак, то в этой точке функция
достигает экстремума:
-если производная меняет знак с «+» на «–», то х0– точка
максимума функции f (х ) ;
- если производная меняет знак с «–» на «+», то х0 – точка
минимума функции f (х ).

9. ПРИЗНАК МАКСИМУМА ФУНКЦИИ

(а;b)
(a; x0)
x0
(x0;b)
f ‘ (x)
+
0
-
f (x)
max
fmax(x) = f (x0)
Поведение функции при её исследовании с помощью производной
на экстремумы проиллюстрируем таблицами:
(а;b)
(a; x0)
x0
(x0;b)
f ‘ (x)
-
0
+
f (x)
min
fmin(x) = f (x0)
ПРИЗНАК МИНИМУМА ФУНКЦИИ

10. АЛГОРИТМ ИССЛЕДОВАНИЯ ФУНКЦИИ НА ТОЧКИ ЭКСТРЕМУМА ПО ГРАФИКУ ПРОИЗВОДНОЙ ФУНКЦИИ

1
Найти область определения функции и интервалы,
на которых функция непрерывна.
2
Найти критические точки, т.е. точки в которых f '(x) = 0
или не существует.
3
Определить знак производной f '(x) на каждом промежутке.
4
Определить точки экстремума.
4.1. Если f ’(x) в точке х0 меняет знак с «+» на «-»,
то х0 – точка максимума.
4.2. Если f ’(x) в точке х0 меняет знак с «-» на «+»,
то х0 – точка минимума.

11.

ОБРАЗЕЦ РЕШЕНИЯ ЗАДАЧИ: На рисунке изображен график
Ответ: X min = -3
производной функции f(x), определенной
на отрезке [−5; 5].
X max = 2,5
Найдите точку минимума и максимума функции f(x) на этом
отрезке .
max
min
1. Выделяем отрезок [−5; 5], на котором функция непрерывна.
2. Отмечаем нули производной, т.е.точки в которых f ’(x) = 0
(точки пересечения с осью Х).
3. Определяем знак производной на каждом промежутке:
3.1. f ’(x) > 0 (график расположен выше оси Х)
3.2. f ’(x) < 0 (график расположен ниже оси Х)
4. Определить точки экстремума.
4.1. Если f ’(x) в точке х0 меняет знак с «+» на «-», то х0 – точка max.
4.2. Если f ’(x) в точке х0 меняет знак с «-» на «+», то х0 – точка min.

12.

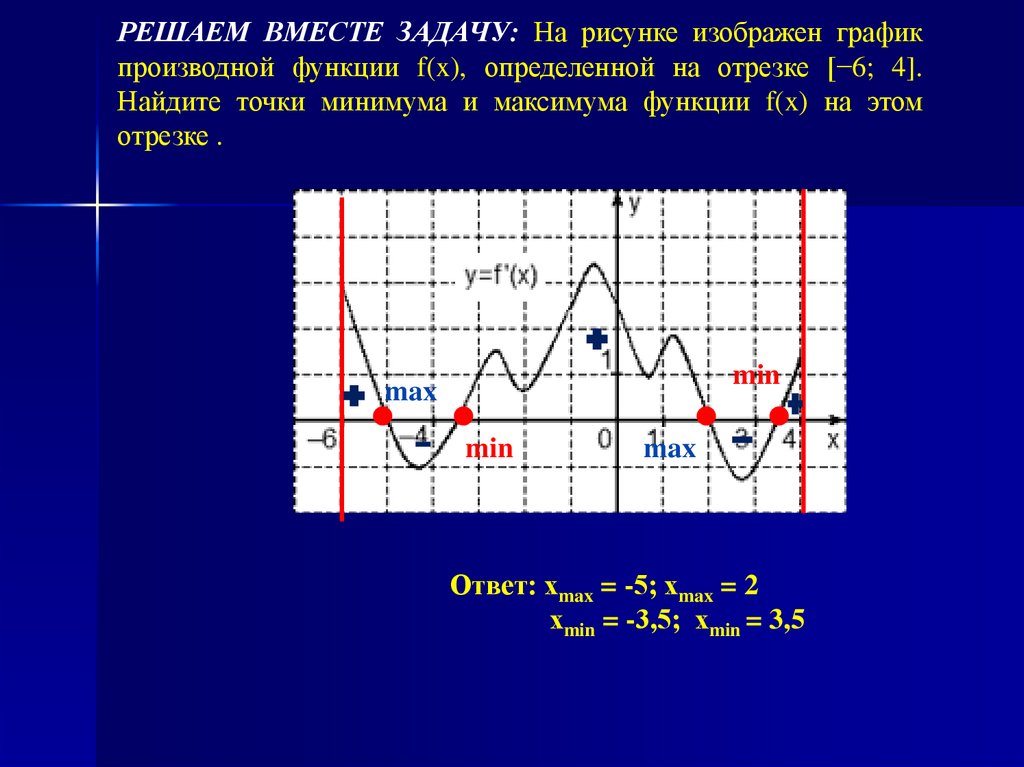
РЕШАЕМ ВМЕСТЕ ЗАДАЧУ: На рисунке изображен график
производной функции f(x), определенной на отрезке [−6; 4].
Найдите точки минимума и максимума функции f(x) на этом
отрезке .
min
max
min
max
Ответ: хmax = -5; хmax = 2
хmin = -3,5; хmin = 3,5

13. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

1
2
3
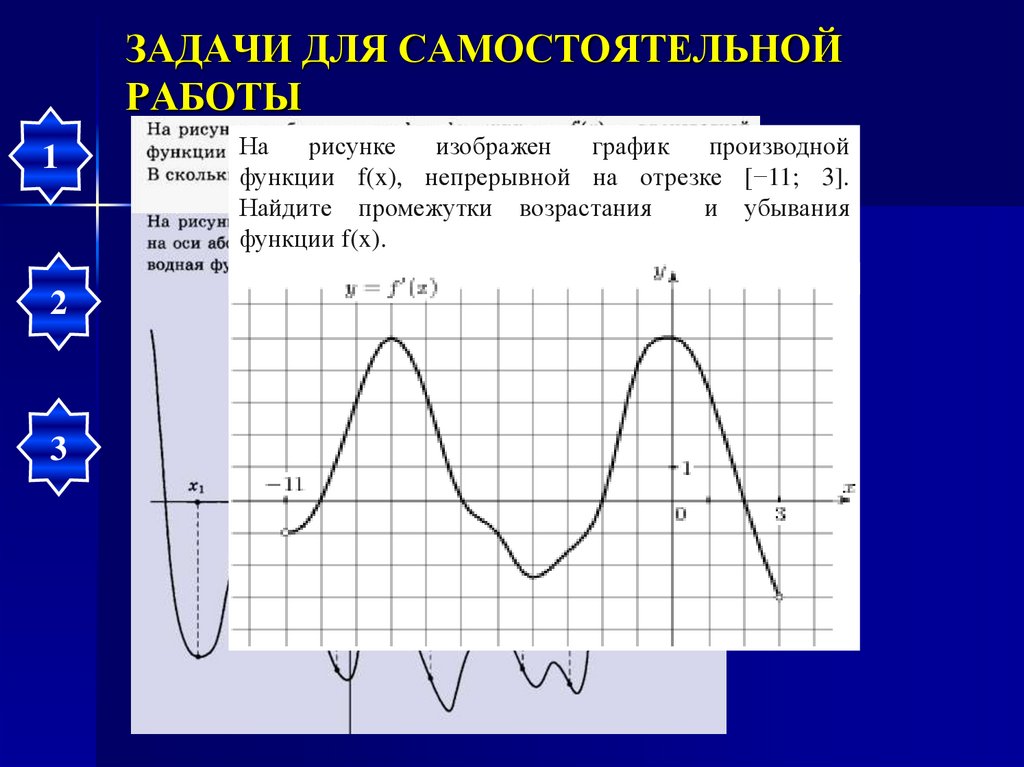
На
рисунке
изображен
график
производной
функции f(x), непрерывной на отрезке [−11; 3].
Найдите промежутки возрастания
и убывания
функции f(x).

14. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

4
5
6
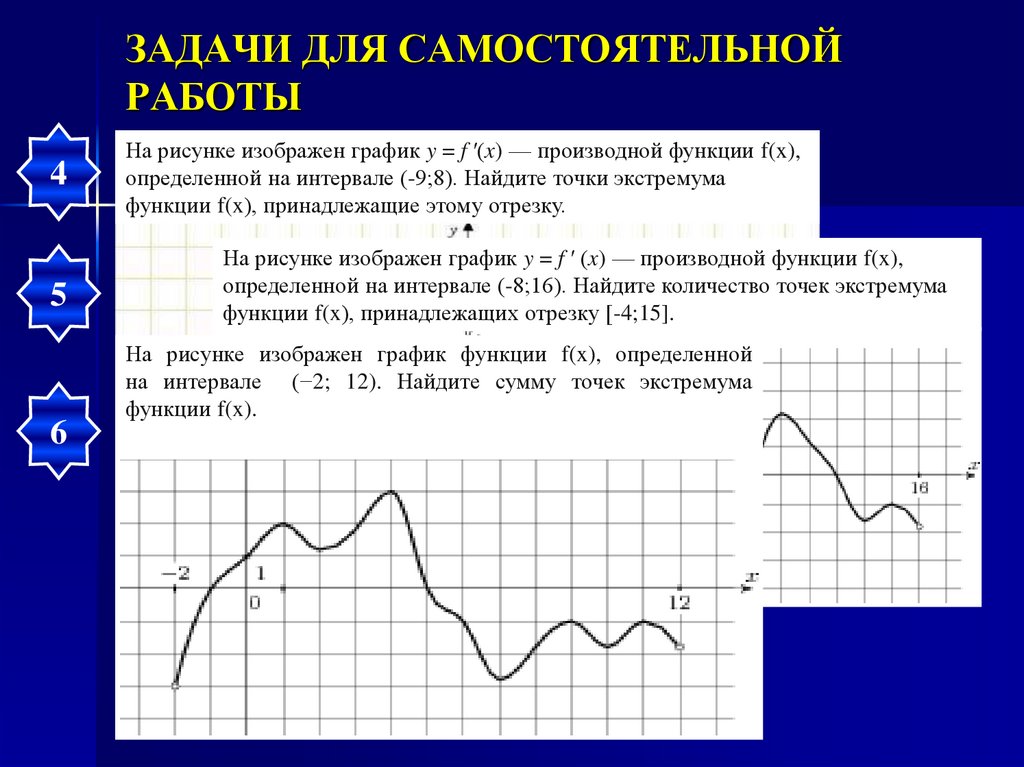
На рисунке изображен график y = f ′(x) — производной функции f(x),
определенной на интервале (-9;8). Найдите точки экстремума
функции f(x), принадлежащие этому отрезку.
На рисунке изображен график y = f ′ (x) — производной функции f(x),
определенной на интервале (-8;16). Найдите количество точек экстремума
функции f(x), принадлежащих отрезку [-4;15].
На рисунке изображен график функции f(x), определенной
на интервале (−2; 12). Найдите сумму точек экстремума
функции f(x).