Похожие презентации:
Механические колебания
1. Механические колебания
2. Механическими колебаниями
называютсядвижения, которые
точно или
приблизительно
повторяются через
одинаковые
промежутки
времени
Ф-11-В Свободные и вынужденные колебания
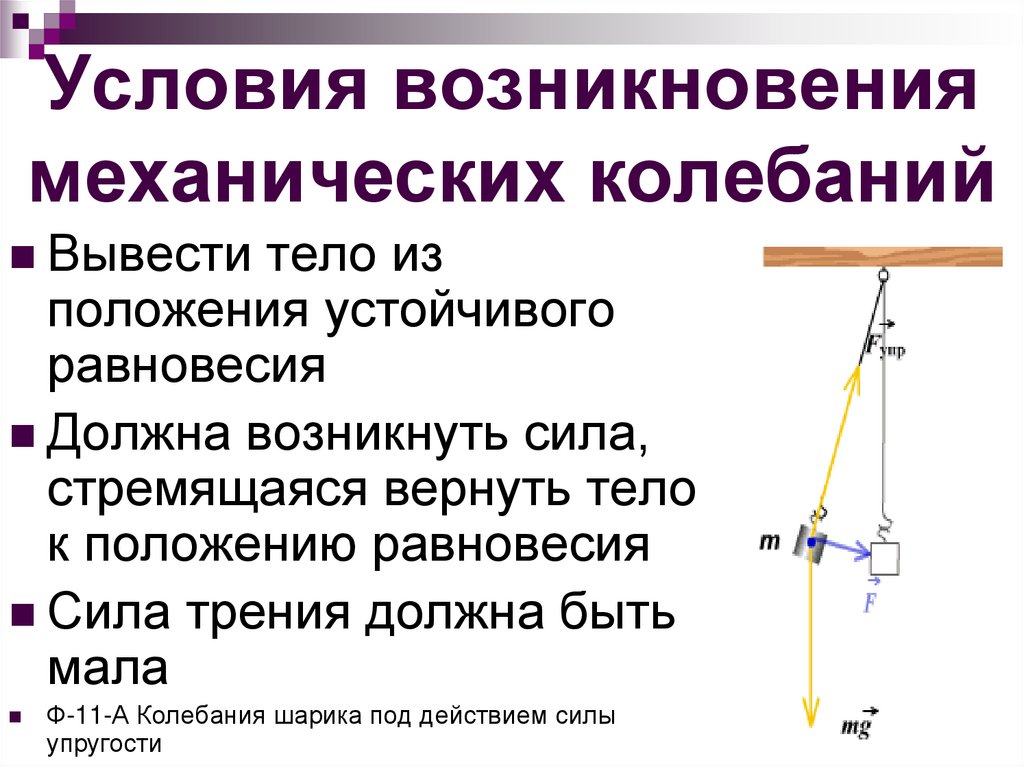
3. Условия возникновения механических колебаний
Вывести тело изположения устойчивого
равновесия
Должна возникнуть сила,
стремящаяся вернуть тело
к положению равновесия
Сила трения должна быть
мала
Ф-11-А Колебания шарика под действием силы
упругости
4. График механических колебаний
5. Виды колебаний
1) Свободные колебания - возникаютпод действием внутренних сил, после
того как система выведена из
положения устойчивого равновесия
(математический маятник, ветка
дерева)
Затухающие
колебания:
Ф-11-А Затухающие колебания
6. Виды колебаний
2) Вынужденные колебания –происходят под действием внешней
периодической силы (поршень ДВС,
игла швейной машинки)
Ф-11-А Примеры незатухающих колебаний
Незатухающие
колебания
7. Величины, характеризующие механические колебания.
Ф-11-В Механическиеколебания. Характеристики
механического колебания
8. Величины, характеризующие механические колебания.
1). Смещение – этоотклонение
колеблющейся
точки от положения
равновесия в
данный момент
времени
Х – смещение – [ м ]
9. Величины, характеризующие механические колебания.
2). Амплитуда – этонаибольшее смещение
точки от положения
равновесия (при
незатухающих
колебаниях амплитуда
постоянна)
Хm – амплитуда – [ м ]
10. Величины, характеризующие механические колебания.
3). Период – это времяодного полного колебания
Т– период – [ с ]
n – количество колебаний - [ ]
t – все время движения - [ с ]
11. Величины, характеризующие механические колебания.
4). Частота – это число полныхколебаний за единицу времени
(ню) – частота – [ Гц ] (Герц)
12. Величины, характеризующие механические колебания.
5). Циклическая частота – это числополных колебаний, которые
совершаются за 2π секунд
ω – циклическая частота – [ C ]
1
13. Величины, характеризующие механические колебания.
6). Фаза колебаний – это физическаявеличина , определяющая отклонение
колеблющейся точки от положения
равновесия в данный момент времени
φ – фаза колебаний – [ рад ]
14. Гармонические колебания
-это колебания, при которых изменения
физических величин происходят по закону
синуса или косинуса
Х = Хm · СОS (ω t + φо)
Х = Хm · Sin (ω t + φо)
15. Задача № 1
Дано:Найти: Х, Хm, Т,
Решение:
t.c
, ω, φ
16. Задача № 1
Дано:Найти: Х, Хm, Т,
, ω, φ
Решение: По графику: Т=4с,
t.c
17. Задача № 1
Дано:Найти: Х, Хm, Т,
, ω, φ
Решение: По графику: Т=4с, Хm = 5м,
t.c
18. Задача № 1
Дано:Найти: Х, Хm, Т,
, ω, φ
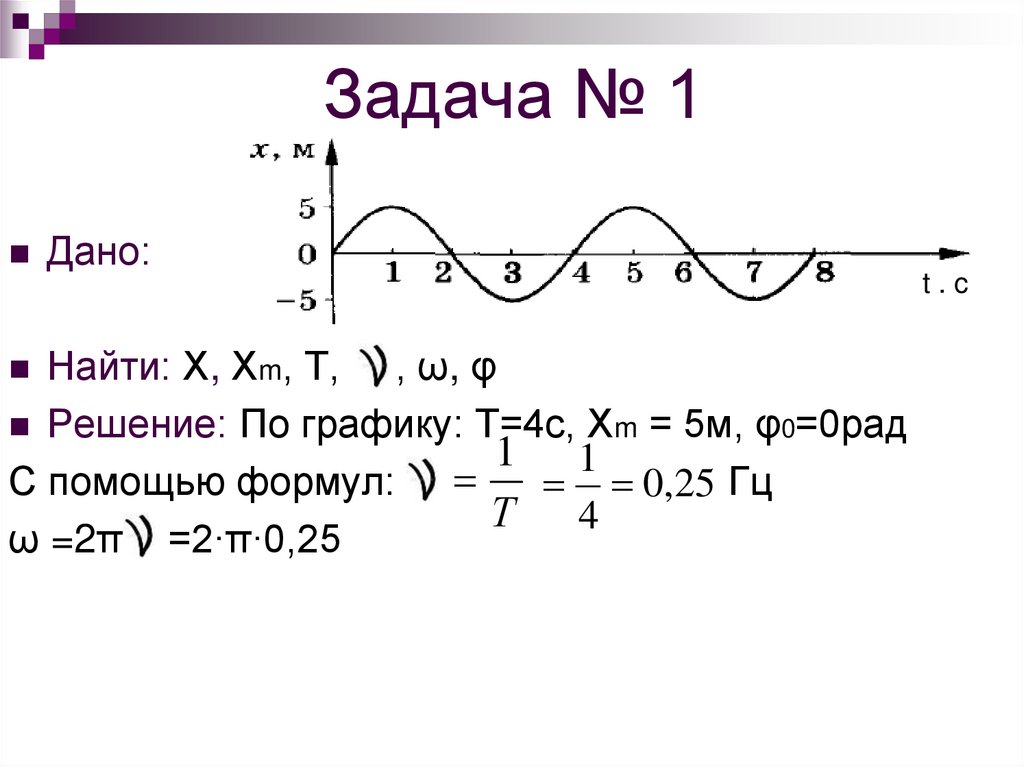
Решение: По графику: Т=4с, Хm = 5м, φ0=0рад
t.c
19. Задача № 1
Дано:t.c
Найти: Х, Хm, Т,
, ω, φ
Решение: По графику: Т=4с, Хm = 5м, φ0=0рад
1
С помощью формул:
Т
20. Задача № 1
Дано:Найти: Х, Хm, Т,
, ω, φ
Решение: По графику: Т=4с, Хm = 5м, φ0=0рад
1 1
С помощью формул:
0,25 Гц
Т 4
t.c
21. Задача № 1
Дано:Найти: Х, Хm, Т,
, ω, φ
Решение: По графику: Т=4с, Хm = 5м, φ0=0рад
1 1
С помощью формул:
0,25 Гц
Т 4
ω =2π
t.c
22. Задача № 1
Дано:Найти: Х, Хm, Т,
, ω, φ
Решение: По графику: Т=4с, Хm = 5м, φ0=0рад
1 1
С помощью формул:
0,25 Гц
Т 4
ω =2π =2∙π∙0,25
t.c
23. Задача № 1
Дано:Найти: Х, Хm, Т,
, ω, φ
Решение: По графику: Т=4с, Хm = 5м, φ0=0рад
1 1
С помощью формул:
0,25 Гц
Т 4
ω =2π =2∙π∙0,25=0,5π
t.c
24. Задача № 1
Дано:Найти: Х, Хm, Т,
, ω, φ
Решение: По графику: Т=4с, Хm = 5м, φ0=0рад
1 1
С помощью формул:
0,25 Гц
Т 4
ω =2π =2∙π∙0,25=0,5π
Х = Хm · sin (ω t + φо) =
t.c
25. Задача № 1
Дано:Найти: Х, Хm, Т,
, ω, φ
Решение: По графику: Т=4с, Хm = 5м, φ0=0рад
1 1
С помощью формул:
0,25 Гц
Т 4
ω =2π =2∙π∙0,25=0,5π
Х = Хm · sin (ω t + φо) = 5
t.c
26. Задача № 1
Дано:Найти: Х, Хm, Т,
, ω, φ
Решение: По графику: Т=4с, Хm = 5м, φ0=0рад
1 1
С помощью формул:
0,25 Гц
Т 4
ω =2π =2∙π∙0,25=0,5π
Х = Хm · sin (ω t + φо) = 5 · sin (
t.c
27. Задача № 1
Дано:Найти: Х, Хm, Т,
, ω, φ
Решение: По графику: Т=4с, Хm = 5м, φ0=0рад
1 1
С помощью формул:
0,25 Гц
Т 4
ω =2π =2∙π∙0,25=0,5π
Х = Хm · sin (ω t + φо) = 5 · sin (0,5π t
t.c
28. Задача № 1
Дано:Найти: Х, Хm, Т,
, ω, φ
Решение: По графику: Т=4с, Хm = 5м, φ0=0рад
1 1
С помощью формул:
0,25 Гц
Т 4
ω =2π =2∙π∙0,25=0,5π
Х = Хm · sin (ω t + φо) = 5 · sin (0,5π t )
t.c
29. Задача № 1
Дано:t.c
Найти: Х, Хm, Т,
, ω, φ
Решение: По графику: Т=4с, Хm = 5м, φ0=0рад
1 1
С помощью формул:
0,25 Гц
Т 4
ω =2π =2∙π∙0,25=0,5π
Х = Хm · sin (ω t + φо) = 5 · sin (0,5π t )
Ответ:Т=4с, Хm =5м, φ0=0рад, ω=0,5π C
=0,25Гц
Х = 5 · sin (0,5π t )
1
30. Колебательные системы
Математический маятник –материальная точка, подвешенная
на невесомой нерастяжимой нити
- длина маятника – [ м ]
g – ускорение свободного падения
g = 9,8 м/с²
1)
31. Колебательные системы
2) Пружинный маятник –это груз, подвешенный
на пружине
k–жесткость пружины-[Н/м]
m – масса груза –[кг]
Ф-11-В Пружинный маятник
32. Колебательные системы
3) Баллистический маятник(Ф-10-В )
33. Превращение энергии при механических колебаниях Ф-10-А Закон сохранения механической энергии
Превращение энергии примеханических колебаниях
1
Ер
Ек
max
0
0
max
max
0
2
3
4
5
Ф-10-А Закон сохранения механической энергии
34. Резонанс
35. Резонанс
36. Резонанс
Резонанс – это явлениевозрастания амплитуды
колебаний при приближении
частоты вынуждающей силы к
собственной частоте
колебательной системы.
Примеры: качели
Ф-11-В Явление механического резонанса
37. Резонанс
С энергетической точки зрениясоздаются наилучшие условия
для передачи энергии от
внешнего источника к
колебательной системе.
38. Явление резонанса
Учитывают при расчетах балок, мостов,станков, перекрытий.




































 Физика
Физика








