Типология школьных математических задач

1. Типология школьных математических задач

Выполнили:
Долгополова Елизавета
Соболева Елена
Новоселова Екатерина
Зиничева Наталия

2. Типы задач, определяемые характером предмета задачи (Г. А. Балл):

Материально направленные задачи
• Предмет задачи материален
Пример («Задачи на составление пропорций», 6 класс):
5м3 бетонной плитки весят 6,5кг . Сколько весят 6м3 плитки?
Информационные задачи
• Предметом
задачи
является
некоторая
модель
какой-либо
моделируемой системы
Пример («Прямоугольный
параллелепипед. Пирамида», 5 класс):

3. Типы задач, определяемые отношениями, существующими между предметом и требованием задачи (Г. А. Балл):

Принципиально неразрешимые
задачи
• В соответствии с закономерностями той области действительности, к
которой относится задача, ее решение невозможно
• невозможно требуемое состояние предмета задачи или невозможен переход к
нему из исходного состояния этого предмета.
Пример (формулировка «задачи, не имеющей решения», из статьи Я.И.
Груденова):
Вычислить сторону прямоугольника, если его площадь равна 435 м2.
Принципиально разрешимые
задачи
• Все задачи, не являющиеся принципиально неразрешимыми,
естественно называть принципиально разрешимыми.

4. Типы задач, определяемые характером требований (Л. М. Фридман):

Задачи на
нахождение
искомого
Задачи на
доказательство
• Требование состоит в том, чтобы найти, разыскать,
распознать какое-то искомое.
• Искомым могут быть величина, отношение, какой-либо
объект, предмет, его положение или форма и т.д.
Пример («Длина окружности. Площадь круга», 6 класс):
Длина окружности равна 100,48 см. Найдите площадь
круга, ограниченного этой окружностью.
• Требование состоит в том, чтобы убедиться в
справедливости
некоторого
утверждения,
или
проверить верность или ложность некоторого
утверждения.
Пример («Первый признак равенства треугольников», 7
класс):
На рисунке АВ=АС, АЕ=АD. Докажите, что BD=CE.

5.

Задачи на
построение
Задачи на
преобразование
• Требование состоит в том, чтобы построить что-либо
(фигуру или выражение).
Пример («Координаты вектора». 9 класс): Начертите
прямоугольную систему координат
и координатные
векторы и . Постройте векторы с началом в точке ,
заданные координатами:
• Требование состоит в том, чтобы преобразовать какоелибо выражение, упростить его, представить в другом
виде.
Пример («Возведение в квадрат и в куб суммы и
разности двух выражений»,7 класс):
Упростите выражения:
1) (х + 3)³ – (х – 3)³
2) (a – 2b)³ + 6ab (a – 2b)

6. Типы задач, определяемые математическим содержанием (А. А. Столяр):

Арифметические
• В основе лежит зависимость между компонентами
арифметических действий.
Пример(«Ряд натуральных чисел», 5 класс):
Около школы растут каштаны и тополя. Каштанов растёт семь, а
тополей – в 3 раза больше. Сколько деревьев растёт около школы?
Алгебраические
• Составление уравнений.
Пример(«Решение уравнений», 6 класс):
Решите с помощью уравнения задачу:
a) На одной полке 42 книги, а на другой - 34. Со второй полки сняли несколько книг, а с
первой - столько, сколько осталось на второй. После этого на первой полке осталось 12 книг.
Сколько книг сняли со второй полки?

7. Типы задач, определяемые математическим содержанием (А. А. Столяр):

Геометрические
• Построение геометрических фигур, охарактеризовать их
свойства.
Пример(«Функция , её график и свойства», 9 класс):
Пересекаются ли парабола и прямая:
y = 50;
Тригонометрические
y = – 8;
y = 14x – 20.
Пример(«Уравнение », 10 класс):
Вычислите:
Комбинаторные
Пример («Комбинаторные задачи», 5 класс):
В отряде космонавтов есть три пилота и два инженера.
Сколько существует способов составить экипаж, состоящий
из одного пилота и одного инженера?

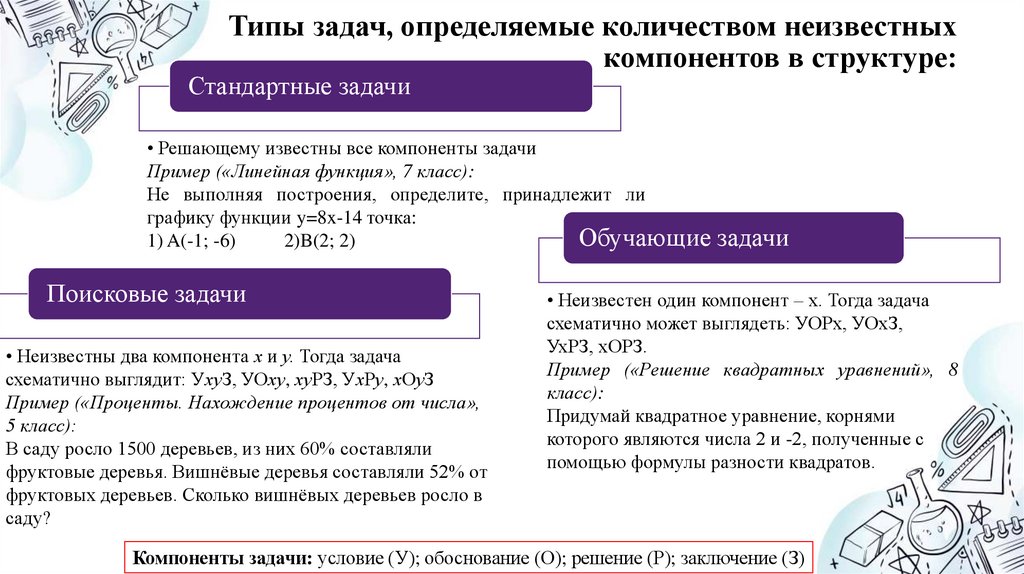
8. Типы задач, определяемые количеством неизвестных компонентов в структуре:

Стандартные задачи
• Решающему известны все компоненты задачи
Пример («Линейная функция», 7 класс):
Не выполняя построения, определите, принадлежит ли
графику функции y=8x-14 точка:
Обучающие задачи
1) A(-1; -6)
2)B(2; 2)
Поисковые задачи
• Неизвестны два компонента х и у. Тогда задача
схематично выглядит: УхуЗ, УОху, хуРЗ, УхРу, хОуЗ
Пример («Проценты. Нахождение процентов от числа»,
5 класс):
В саду росло 1500 деревьев, из них 60% составляли
фруктовые деревья. Вишнёвые деревья составляли 52% от
фруктовых деревьев. Сколько вишнёвых деревьев росло в
саду?
• Неизвестен один компонент – х. Тогда задача
схематично может выглядеть: УОРх, УОхЗ,
УхРЗ, хОРЗ.
Пример («Решение квадратных уравнений», 8
класс):
Придумай квадратное уравнение, корнями
которого являются числа 2 и -2, полученные с
помощью формулы разности квадратов.
Компоненты задачи: условие (У); обоснование (О); решение (Р); заключение (З)

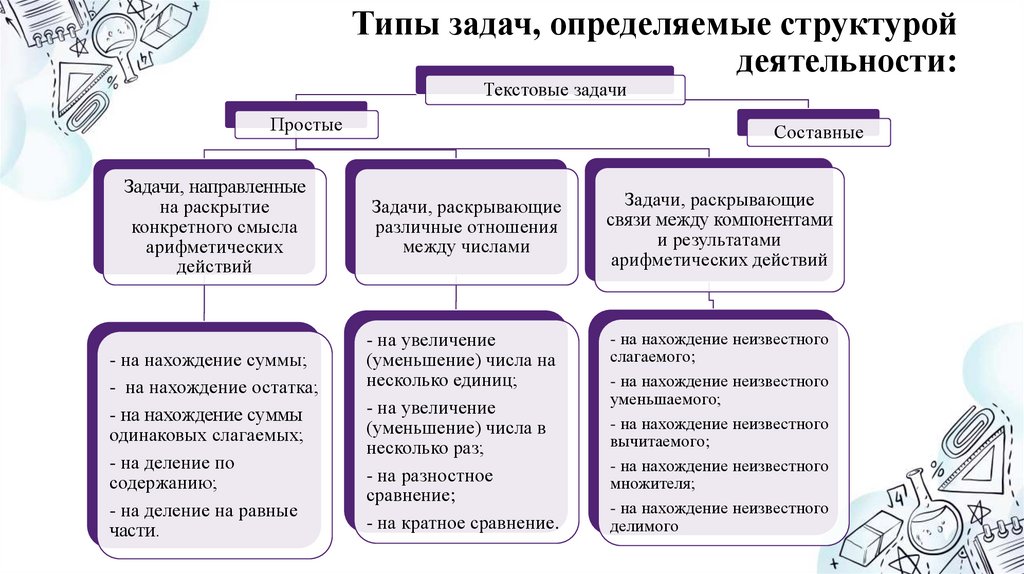
9. Типы задач, определяемые структурой деятельности:

Текстовые задачи
Простые
Задачи, направленные
на раскрытие
конкретного смысла
арифметических
действий
- на нахождение суммы;
- на нахождение остатка;
- на нахождение суммы
одинаковых слагаемых;
- на деление по
содержанию;
- на деление на равные
части.
Составные
Задачи, раскрывающие
различные отношения
между числами
Задачи, раскрывающие
связи между компонентами
и результатами
арифметических действий
- на увеличение
(уменьшение) числа на
несколько единиц;
- на увеличение
(уменьшение) числа в
несколько раз;
- на разностное
сравнение;
- на кратное сравнение.
- на нахождение неизвестного
слагаемого;
- на нахождение неизвестного
уменьшаемого;
- на нахождение неизвестного
вычитаемого;
- на нахождение неизвестного
множителя;
- на нахождение неизвестного
делимого

10. Примеры текстовых задач:

Простые:
2 класс
• Задачи, направленные на раскрытие конкретного смысла арифметических
действий: Мама пришила 6 пуговиц к пальто и 2 пуговицы к плащу. Сколько всего
пуговиц пришила мама?
4 класс
• Задачи, раскрывающие различные отношения между числами: В одном автобусе 48
пассажиров, а в другом – в 3 раза больше. На сколько человек в первом автобусе
меньше, чем во втором?
4 класс
• Задачи, раскрывающие связи между компонентами и результатами арифметических
действий: В школьном саду посадили 30 яблонь, 10 слив и несколько вишен.
Сколько посадили вишен, если всего было посажено 48 деревьев? 60 деревьев?
Составные:
• В ателье было 240 м ситца. Когда сшили несколько платьев,
расходуя на каждое по 3 м, то осталось ещё 90 м ситца. Сколько
4 класс платьев сшили?

11.

Типы задач, определяемые фабулой задачи:
На движение
• «Линейное уравнение с одной переменной», 7 класс:
• Велосипедист проехал 65 км за 5ч. Часть пути он ехал со скоростью 10 км/ч, а
оставшийся путь – со скоростью 15 км/ч. Сколько времени он ехал со скоростью 10
км/ч и сколько – со скоростью 15 км/ч?
На прибыль
• «Сложение и вычитание десятичных дробей», 5 класс:
• В декабре фермер получил прибыль в размере 438,86 тысячи рублей, а в январе – на
16,4 тысячи рублей больше, чем в декабре. Сколько тысяч рублей составила прибыль
фермера за декабрь и январь вместе?
На площадь
• «Площадь прямоугольника», 6 класс:
• Какой участок имеет большую площадь: прямоугольный со сторонами 8 м и 9 м или
квадратный со стороной 9 м?
На работу
• «Задачи на работу», 9 класс:
• Бригада рабочих за 5 дней изготовила меньше 300 деталей, а за 10 дней – больше 500
деталей. Сколько деталей в день изготовил каждый рабочий, если в бригаде 8 человек
и производительность труда рабочих одинакова?
На проценты
• «Процентное отношение двух чисел», 6 класс:
• Костюм стоил 1800р. Сначала его цену повысили на 20 %, а потом новую цену
снизили на 10%.Какой стала цена костюма после этих изменений? На сколько
процентов изменилась начальная цена костюма?

12. Типы задач, определяемые фабулой задачи:

На кредит
• «Финансовая математика», 11 класс:
• Ольга планирует взять в кредит 100 000 рублей под 10% годовых. Погашение
кредита происходит раз в год равными суммами (кроме, может быть, последней)
после начисления процентов. На какое минимальное количество лет Ольга может
взять кредит, чтобы ежегодные выплаты были не более 24 тысяч рублей?
На смеси и сплавы
• «Процентное отношение двух чисел», 6 класс:
• К сплаву массой 600 г, содержавшему 20% меди, добавили 40 г меди. Каким стало
процентное содержание меди в новом сплаве?
На смешение и
концентрацию
• «Решение задач с помощью уравнений», 7 класс:
• Иван случайно смешал молоко жирностью 2,5% и молоко жирностью 6%. В итоге
у него получилось 5 литров молока жирностью 4,6%. Сколько литров молока
жирностью 2,5% было у Ивана до смешивания?
На покупку и
продажу
• «Сложение натуральных чисел», 5 класс:
• В магазине бытовой техники кофеварки продаются по цене 3200 рублей а чайники
по цене 1500 рублей. За месяц продали 15 кофеварок и 23 чайника. Сколько денег
выручил магазин за продажу этих товаров?