Похожие презентации:
Формулы для радиусов вписанной и описанной окружности треугольника
1.
Формулы для радиусов вписанной иописанной окружности треугольника
2. Описанная окружность. Треугольник, вписанный в окружность.
• Окружность называется описаннойоколо
треугольника,
если
она
проходит через все его вершины. В
этом случае треугольник называется
вписанным в окружность.
• Стороны вписанного треугольника
являются хордами описанной около
него окружности.
• Где
лежит
центр
окружности,
описанной около треугольника?
3.
ВА
А
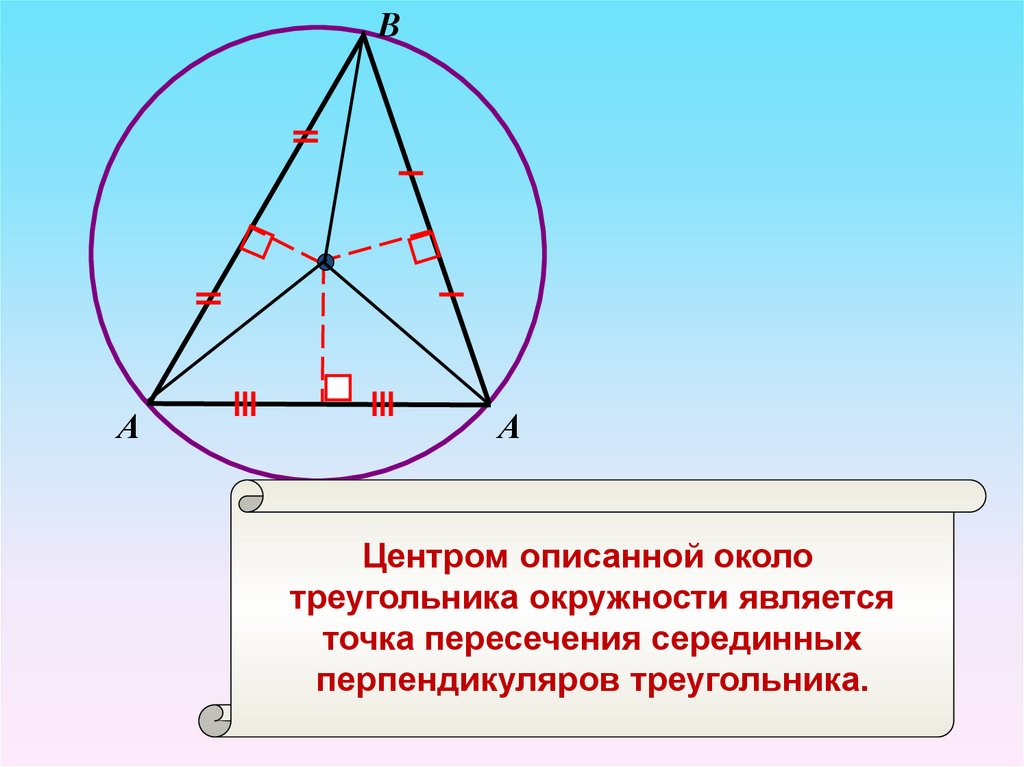
Центром описанной около
треугольника окружности является
точка пересечения серединных
перпендикуляров треугольника.
4.
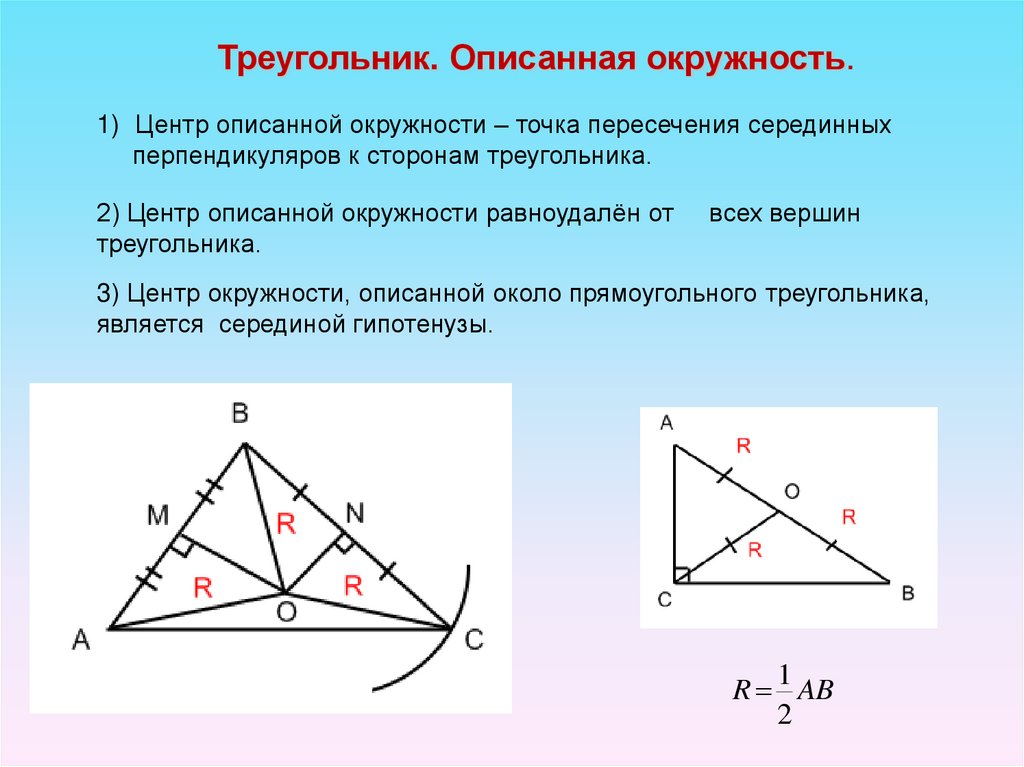
Треугольник. Описанная окружность.1) Центр описанной окружности – точка пересечения серединных
перпендикуляров к сторонам треугольника.
2) Центр описанной окружности равноудалён от
треугольника.
всех вершин
3) Центр окружности, описанной около прямоугольного треугольника,
является серединой гипотенузы.
1
R AB
2
5. Окружность, вписанная в треугольник.
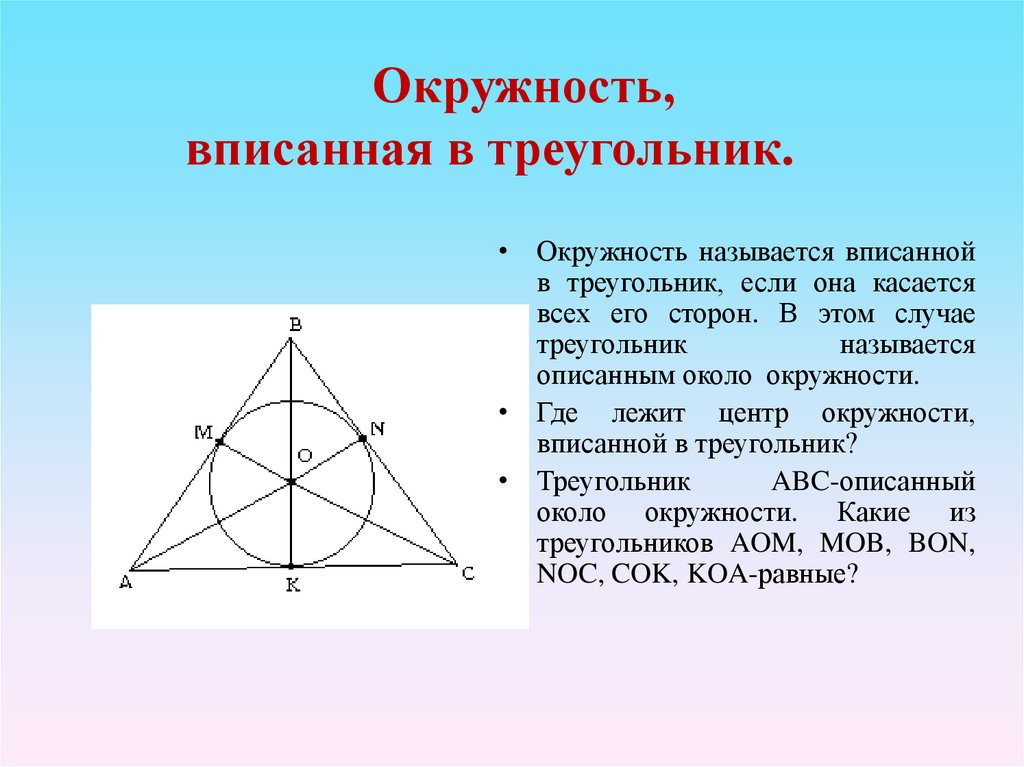
• Окружность называется вписаннойв треугольник, если она касается
всех его сторон. В этом случае
треугольник
называется
описанным около окружности.
• Где лежит центр окружности,
вписанной в треугольник?
• Треугольник
ABC-описанный
около окружности. Какие из
треугольников AOM, MOB, BON,
NOC, COK, KOA-равные?
6.
ВК
С
М
О
Р
А
Центром вписанной в треугольник
окружности является точка
пересечения биссектрис
треугольника.
7.
В любой треугольник можновписать окружность.
8.
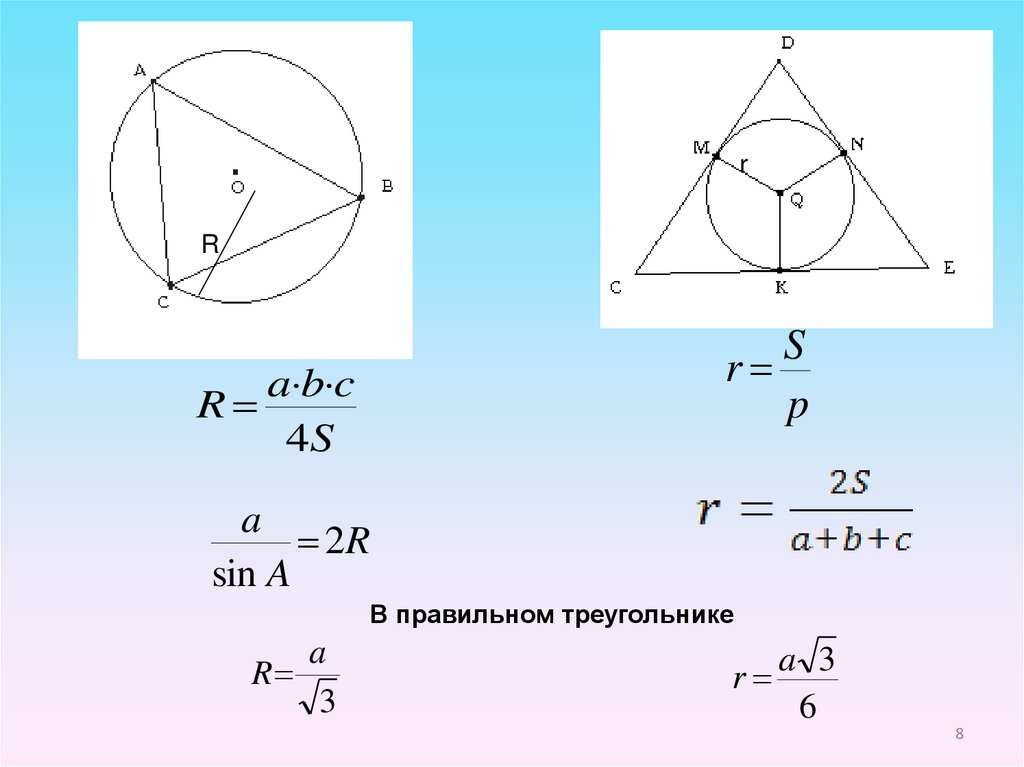
rR
S
r
p
a b c
R
4S
a
2R
sin A
В правильном треугольнике
a
R
3
r
a 3
6
8
9.
№ 1. В равносторонний треугольник со стороной 4 см вписанаокружность. Найдите её радиус.
Решение:
a2 3
S=
4
и
S=p·r
42 3 =
S=
4 3
4
r
а
P = ½ ·4 · 3 = ½ · 12 = 6(см) - полупериметр
4 3 6 r
r=
4 3 2 3
(см)
6
3
Ответ:
2 3
3
(см)
10. №2. Окружность, вписанная в треугольник АВС, касается сторон АВ, ВС и АС в точках М, К и Р соответственно. Найдите периметр
треугольника АВС, если АР = 4 см, ВМ = 6 см, СК = 3 см.А
М
4
Отрезки касательных,
проведенных из одной точки
равны.
4
Р
6
3
В
6
К
3
С
ВМ = ВК
АМ = АР
СР = СК
АВ = 10
АС = 7
ВС = 9
Р = 10 + 7 + 9 = 26
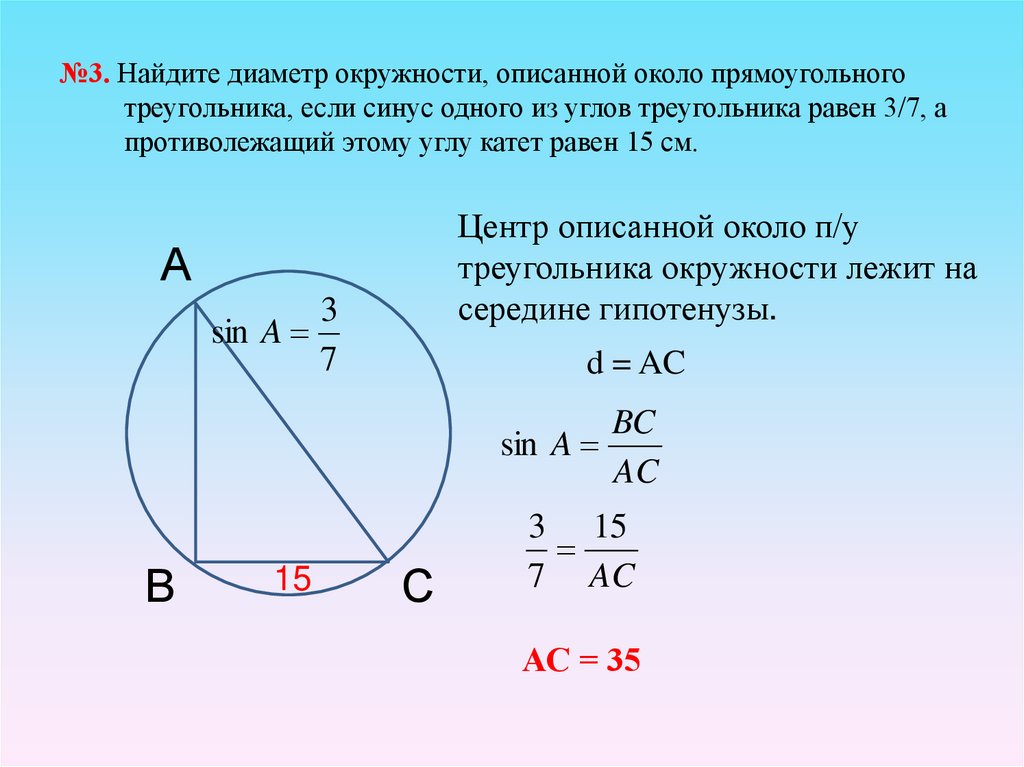
11. №3. Найдите диаметр окружности, описанной около прямоугольного треугольника, если синус одного из углов треугольника равен 3/7,
апротиволежащий этому углу катет равен 15 см.
Центр описанной около п/у
треугольника окружности лежит на
середине гипотенузы.
А
3
sin A
7
d = AC
BC
sin A
AC
В
15
С
3 15
7 AC
АС = 35
12. №4. Найдите радиус окружности, описанной около треугольника, если одна из сторон треугольника равна 20 см, а расстояние от
центраокружности до этой стороны равно 24 см.
Т.к. ОК АС, то
АК=КС=10
В
24
А
20 К
по т. Пифагора
0
ОС = 102 242 26
С
13.
+№4414.
Домашнее задание№43 стр. 208









 Математика
Математика








