Похожие презентации:
Программный инструментарий решения задач транспортного типа. Лекция 2.1
1.
Кафедра информатики ивычислительной техники
Информационные системы и технологии
поддержки принятия решений в области
ГОЧС
Тема 2. Программный инструментарий
решения задач транспортного типа
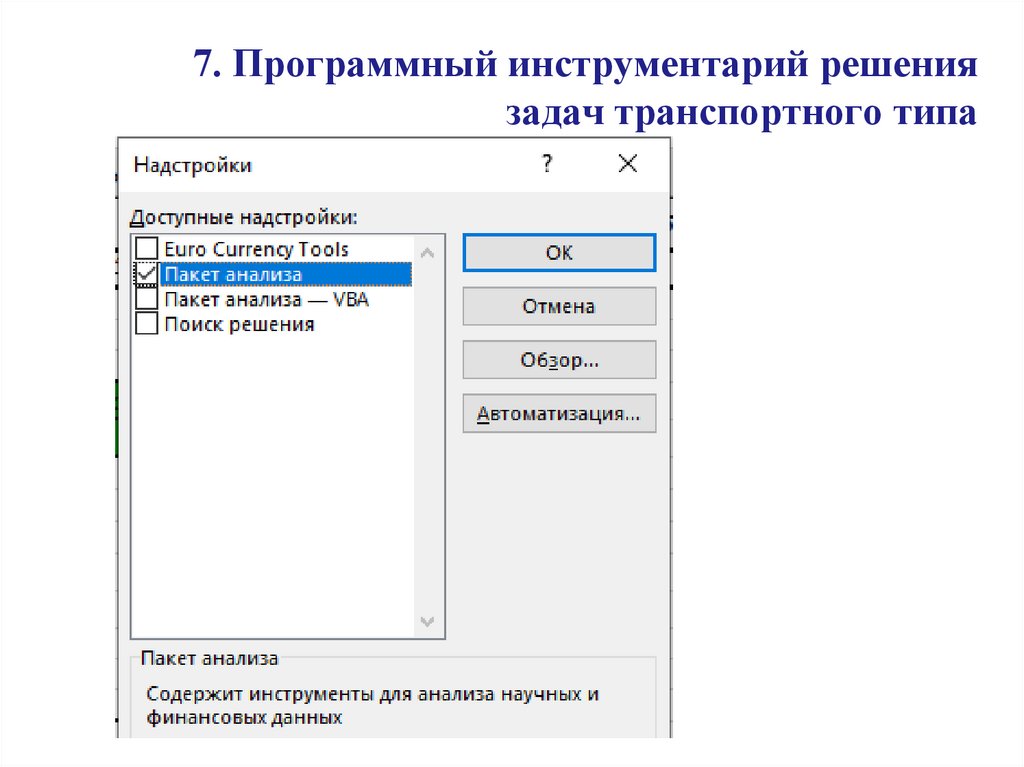
Лекция 2.1. Программный инструментарий
решения задач транспортного типа
Заведующий кафедрой к.п.н., доцент
Безвесильная Анжела Александровна
2. Литература
1.Мадера А.Г. Моделирование и принятие решений в менеджменте:
Руководство для будущих топ-менеджеров. – М.: Издательство ЛКИ, 2010. –
688 с.
2.
Черноруцкий И.Г. Методы принятия решений. – СПб.: БХВПетербург, 2005.
3.
Урубков А. Курс МВА по оптимизации управленческих решений.
Практическое руководство по использованию моделей линейного
программирования. М.: Альпина Паблишер, 2012. – 174 с.
4.
Сеcлавин А.И. Сеславина Е.А. Оптимизация и математические
методы принятия решений. Учебное пособие. – М: МИИТ. 2011. - 152.
2
3. Учебные вопросы
1.Особенности и основные правила построениямоделей транспортного типа
2. Области применения моделей транспортного типа
3. Достоинства и недостатки моделей транспортного
типа
4. Задача о смесях
5. Транспортная задача
6. Задача о назначениях
7. Программный инструментарий решения задач транспортного типа
3
4. 1.Особенности и основные правила построения моделей транспортного типа
Под термином "транспортные задачи" понимается широкийкруг задач не только транспортного характера. Общим для
них является, как правило, распределение ресурсов,
находящихся у m производителей (поставщиков), по n
потребителям этих ресурсов.
Транспортная задача является важнейшей частной
задачей линейного программирования, имеющей
обширные практические приложения не только к
проблемам транспорта.
Она выделяется в линейном программировании
определённостью экономической характеристики,
особенностями математической модели, наличием
специфических методов решения.
3
5. 1.Особенности и основные правила построения моделей транспортного типа
К ЗЛП транспортного типа приходят при рассмотренииразличных практических ситуаций, связанных
с составлением наиболее экономичного плана
перевозок продукции,
управления запасами,
назначением персонала на рабочие места,
оборотом наличного капитала и многими другими.
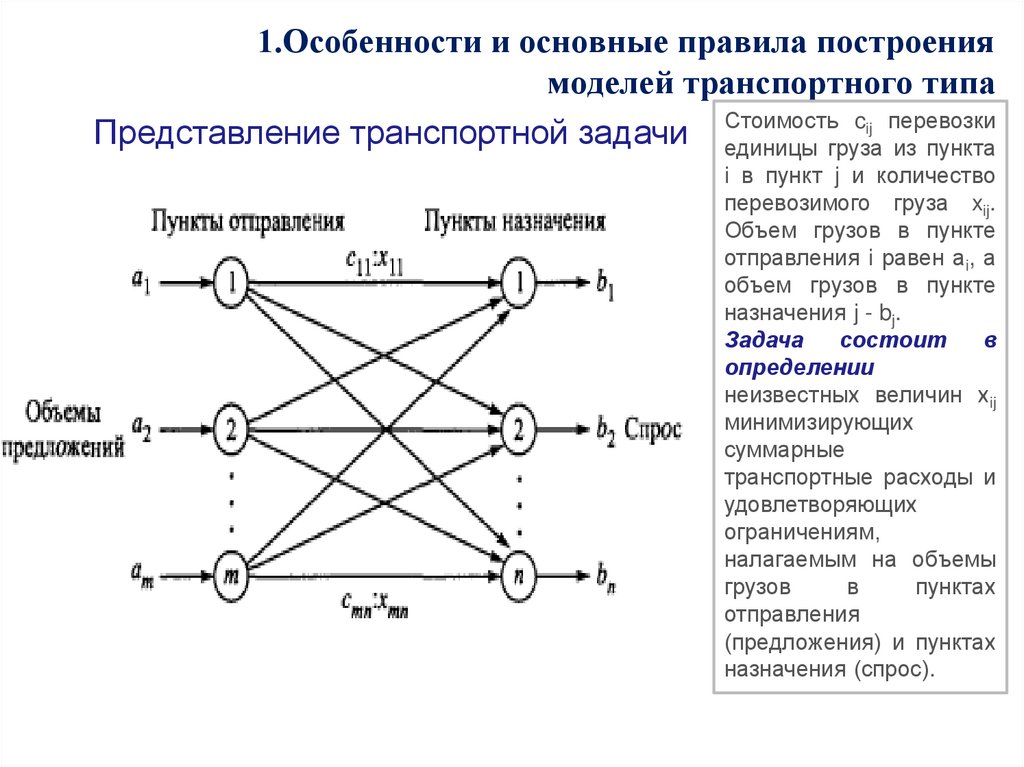
6. 1.Особенности и основные правила построения моделей транспортного типа
cij перевозкиПредставление транспортной задачи Стоимость
единицы груза из пункта
i в пункт j и количество
перевозимого груза xij.
Объем грузов в пункте
отправления i равен аi, а
объем грузов в пункте
назначения j - bj.
Задача
состоит
в
определении
неизвестных величин хij
минимизирующих
суммарные
транспортные расходы и
удовлетворяющих
ограничениям,
налагаемым на объемы
грузов
в
пунктах
отправления
(предложения) и пунктах
назначения (спрос).
7. 1.Особенности и основные правила построения моделей транспортного типа
В общем виде исходные данные транспортнойзадачи представлены в табл.
Транспортная таблица
8. 1.Особенности и основные правила построения моделей транспортного типа
математическая модель транспортной задачиформулируется следующим образом:
Первое ограничение означают, что суммарный объем перевозок от i -го
поставщика не может превышать имеющегося у него запаса товара ai. Второе
ограничение означают, что суммарные перевозки товара j-му потребителю
должны полностью удовлетворить его потребности в товаре bj. Третье
ограничение исключает обратные перевозки.
9. 1.Особенности и основные правила построения моделей транспортного типа
Из первых двух ограничений следует, что:то
модель
называется
сбалансированной
транспортной моделью. В сбалансированной модели
первые два ограничения имеют вид равенств. В
реальных условиях запас товара не всегда равен спросу
(потребности), но транспортную модель всегда можно
сбалансировать.
10. 1.Особенности и основные правила построения моделей транспортного типа
11. 1.Особенности и основные правила построения моделей транспортного типа
Отметим, несбалансированную транспортную задачуназывают также открытой транспортной задачей,
тогда как сбалансированную транспортную задачу закрытой транспортной задачей.
Стремление сбалансировать транспортную задачу
обусловлено возможностью применить в этом случае
эффективный вычислительный метод.
12. 1.Особенности и основные правила построения моделей транспортного типа
Наиболее распространенным методомрешения транспортных задач является
метод потенциалов, который был
предложен в 1949 г. советскими
математиками Л.В. Канторовичем (19121986) 1975 год Нобелевская премия по экономике
и М.К. Гавуриным (1911-1992).
Позже аналогичный метод разработал
американский математик Дж. Данциг
(1914-2005), основываясь на общих идеях
линейного программирования.
Л.В. Канторович
М.К. Гавурин
13. 2. Области применения моделей транспортного типа
Транспортная задача находит свое применение во многих областяхэкономики.
Существует большое количество прикладных экономических задач,
которые в итоге сводятся к транспортной задаче, некоторые из них:
Задача оптимального распределения оборудования: оборудование т
различных видов нужно распределить между п рабочими участками так,
чтобы суммарная производительность оказалась максимальной
Задача оптимального распределения работ: требуется распределить т
работ (или исполнителей) по п станкам (или участкам) так, чтобы
суммарные затраты выполнения работ были минимальны.
Задача оптимального распределения торговых агентов: необходимо
определить план продаж товара в нескольких городах с известной
покупательной способностью жителей и известным профессиональным
уровнем агентов, чтобы получить максимальный ожидаемый доход от
продажи товаров.
Задача оптимального размещения производства: требуется разработать план
выпуска п новых видов продукции на т предприятиях при известных издержках
производства и сбыта единицы продукции каждого вида, предполагаемом спросе
на продукцию каждого вида и прогнозируемой цене за единицу продукции,
максимизирующий ожидаемую прибыль.
14.
Выделяют два типа транспортныхзадач:
по критерию стоимости - план
перевозок является оптимальным,
если достигается минимум затрат на
его реализацию;
по критерию времени - план
перевозок оптимален, если на него
затрачивается минимальное
количество времени.
15. 3. Достоинства и недостатки моделей транспортного типа
Для того чтобыэффективно
использовать все
ресурсы и
минимизировать затраты
на транспортировку
необходимо ссылаться на
транспортную задачу.
Она, позволяет
оптимизировать
транспортные расходы и
тем самым свести к
минимуму все затраты в
ресурсные
ограничения могут
свести решение на
нет
делимость проекта
не всегда
возможна.
16. 4. Задача о смесях
К группе задач о смесях относят задачи поотысканию наиболее дешевого набора из
определенных
исходных
материалов,
обеспечивающих получение смеси с заданными
свойствами.
Иными словами, получаемые смеси должны иметь
в своем составе m различных компонентов в
определенных количествах, а сами компоненты
являются составными
материалов.
частями
n
исходных
17.
Задачи составления оптимальных композиций изматериалов, которые должны обладать определёнными
свойствами и минимальной себестоимостью образуют
подкласс задач о смесях.
Число исходных материалов может быть достаточно
большим, и поэтому решить такую задачу перебором
вариантов представляется возможным лишь в
приближённом виде. Причём неизвестно, насколько
близким к оптимальному получится решение. Как
правило, на производстве такие задачи решаются
квалифицированными специалистами.
18.
Для формализации решения задач этого класса можно предложитьмодель математического программирования в целочисленной
постановке.
Пусть имеется групп исходных материалов, в каждую из которых входит
видов однотипных материалов, отличающихся своими
характеристиками.
Из этих материалов необходимо получить изделие, обладающее
свойствами, которые зависят от характеристик исходных материалов.
Эти зависимости определяются специалистами-технологами на
производстве экспериментальным путём. Из каждой группы материалов
нужно выбрать всего один.
Пусть заданы свойств, которыми должно обладать вырабатываемое
изделие, их значения не должны быть ниже некоторой определённой
границы качества. Каждый из исходных материалов имеет значение
соответствующих свойств. Считаем зависимость свойств
вырабатываемого изделия от свойств исходных материалов линейной.
Обозначим – коэффициенты, характеризующие влияние свойств
исходных материалов на свойства вырабатываемого изделия; – цена r-го
материала из i-й группы; – r-й материал из i-й группы.
19. 5. Транспортная задача
Транспортная задача(классическая) — задача об
оптимальном плане перевозок
однородного продукта из однородных
пунктов наличия в однородные пункты
потребления на однородных
транспортных средствах
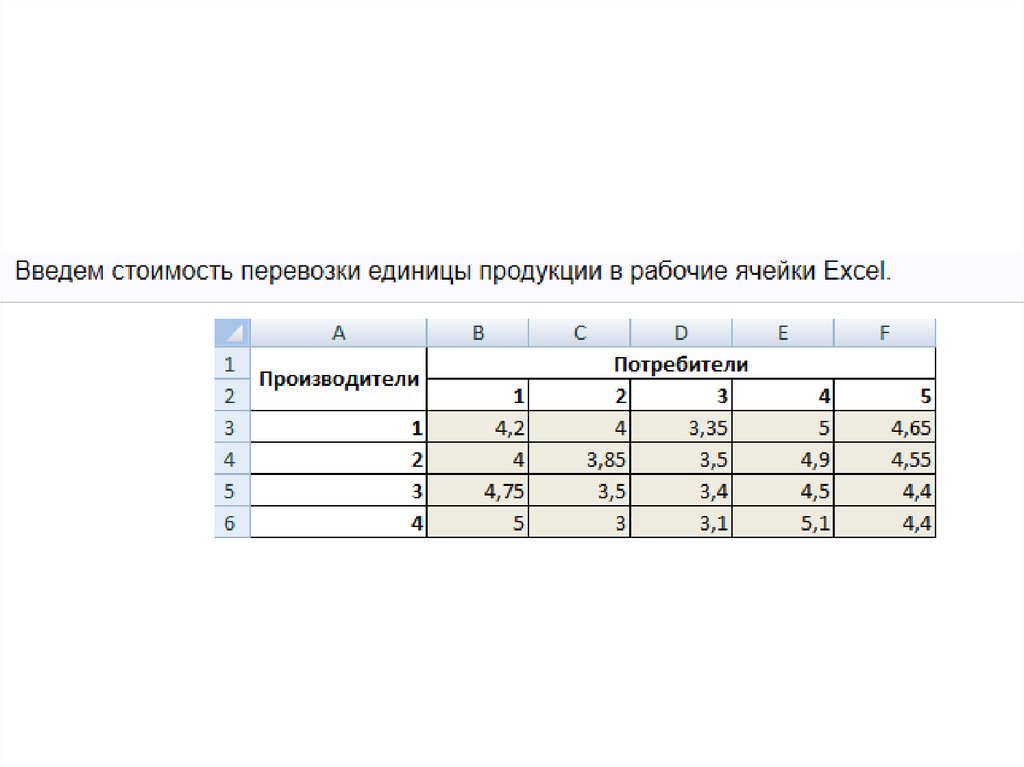
20. Условие задачи
Готовая продукция с заводов-изготовителей,расположенных в городах i1, i2, i3 и i4, запасы
которой на заводах составляют z1, z2, z3 и z4 т
соответственно,
поставляется
заказчикам,
расположенным в городах g1, g2, g3, g4 и g5,
имеющим потребности в продукции, равные p1, p2,
p3, p4 и p5 т соответственно. Тарифы (ден. ед./т) на
перевозку продукции между городами-поставщиками
и городами-потребителями приведены в таблице:
21.
Заказчики, расположенные в городахЗаводыизготовители
g1
g2
g3
g4
g5
i1
c11
c12
c13
c14
c15
i2
c21
c22
c23
c24
c25
i3
c31
c32
c33
c34
c35
i4
c41
c42
c43
c44
c45
22. Постановка задачи
Имеется 5 складов содержащихнекоторое количество единиц
однотипной продукции,
имеется также 4 потребителя
нуждающиеся в определенном
количестве данной продукции.
Величина издержек приведена в таблице
3.
23. Шаг 1. Проверка на сбалансированность
Общее число запасов на складах = 790Общая потребность = 790
Задача является сбалансированной
(закрытой)
24. Шаг 2. Отыскание начального решения. Метод минимального элемента.
Выберем клетку в которойбудем распределять
продукцию, это клетка
содержит минимальное
значение издержек.
На рисунке сама клетка и
соответствующие ей
остатки отображены
красным цветом.
25. Шаг 2. Отыскание начального решения. Метод минимального элемента
Итерация 11. Заполняем клетку a1b1.
2. Сравниваем значения остатков для
производителя a1 и потребителя b1.
3. Нераспределенные остатки по
запасам a1 меньше, запишем меньшее
число в клетку a1b1 одновременно
вычитая его из обеих клеток остатков.
4. Клетка остатков по запасам
обнулиться указывая, что все запасы
производителя a1 использованы.
Исключаем строку a1 из дальнейшего
рассмотрения (серый тон).
5. Ненулевое значение остатка по
потребностям для b1 показывает,
сколько единиц продукции еще
требуется
26. Шаг 2. Отыскание начального решения. Метод минимального элемента
Итерация 2Заполняем клетку
a2b1.
27. Шаг 2. Отыскание начального решения. Метод минимального элемента
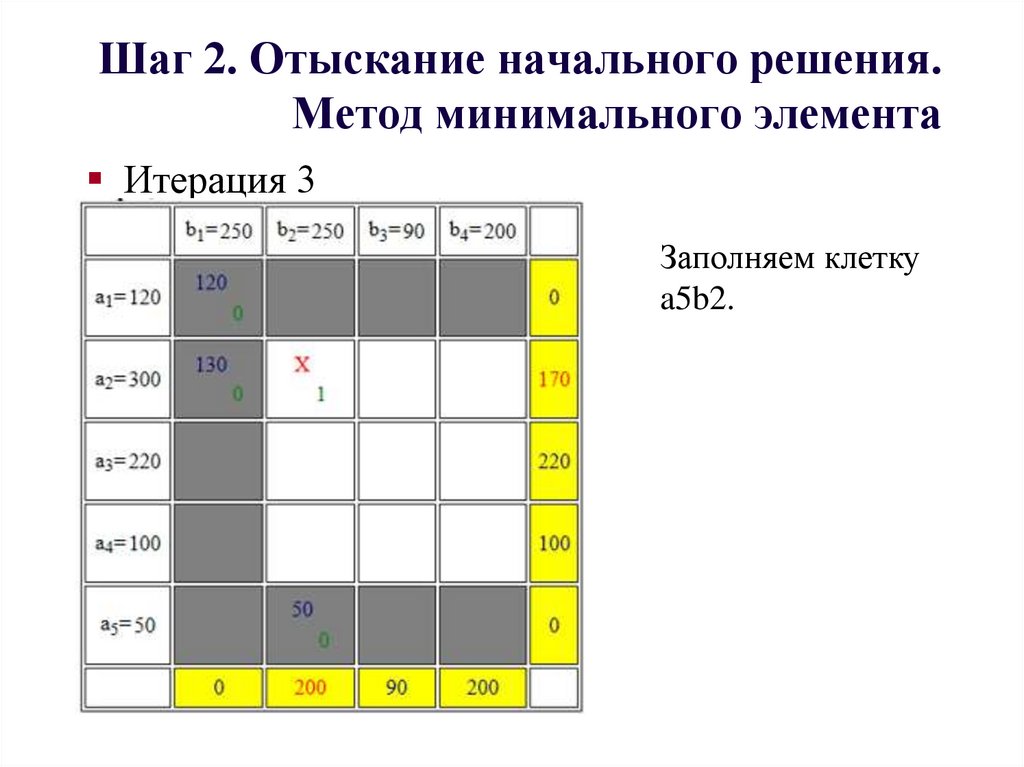
Итерация 3Заполняем клетку
a5b2.
28. Шаг 2. Отыскание начального решения. Метод минимального элемента
Итерация 4Заполняем клетку
a2b2.
29. Шаг 2. Отыскание начального решения. Метод минимального элемента
Итерация 5Заполняем клетку
a3b2.
30. Шаг 2. Отыскание начального решения. Метод минимального элемента
Итерация 6Заполняем клетку
a3b4.
31. Шаг 2. Отыскание начального решения. Метод минимального элемента
Итерация 7Заполняем клетку
a4b3.
32. Шаг 2. Отыскание начального решения. Метод минимального элемента
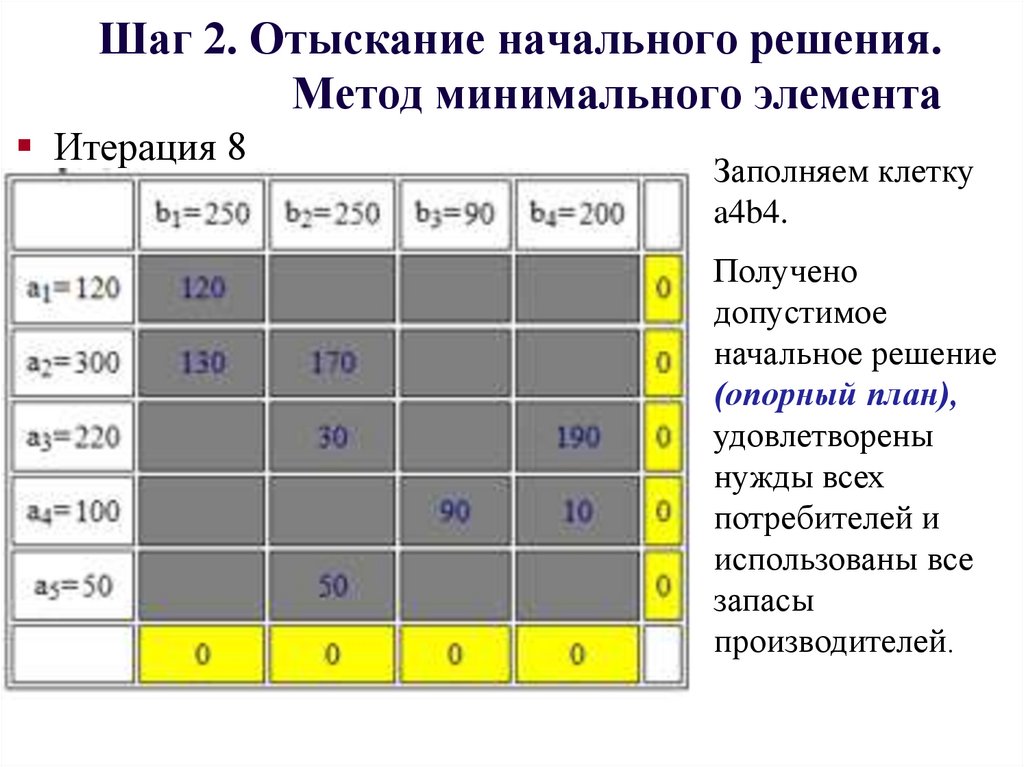
Итерация 8Заполняем клетку
a4b4.
Получено
допустимое
начальное решение
(опорный план),
удовлетворены
нужды всех
потребителей и
использованы все
запасы
производителей.
33. Шаг 3. Проверка опорного плана на вырожденность
Проверим опорный план на вырожденность.Количество заполненных клеток N должно
удовлетворять условию N=n+m-1.
В нашем случае N=8,
n+m=4+5=9,
Следовательно наш план
невырожденный.
34. Шаг 4. Вычислим общие затраты на перевозку продукции
Перемножим числастоящие в одной
клетке, затем
полученные
произведения сложим.
Получим значение
суммарных затрат для
данного начального
решения.
Рнач. = 800
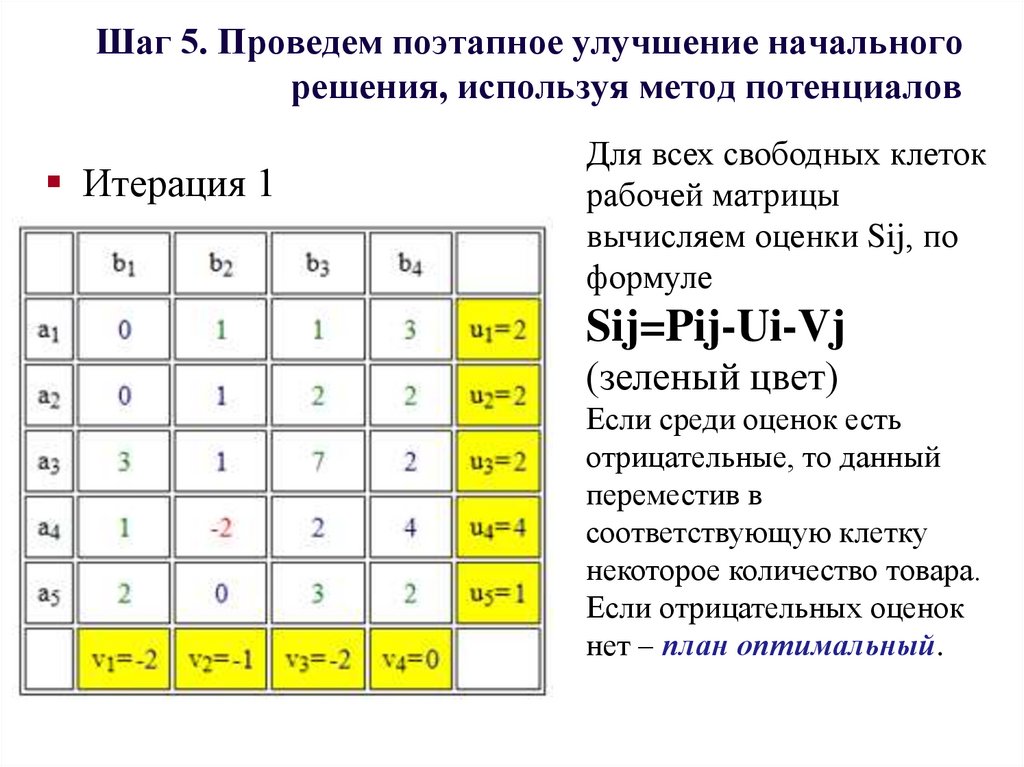
35. Шаг 5. Проведем поэтапное улучшение начального решения, используя метод потенциалов
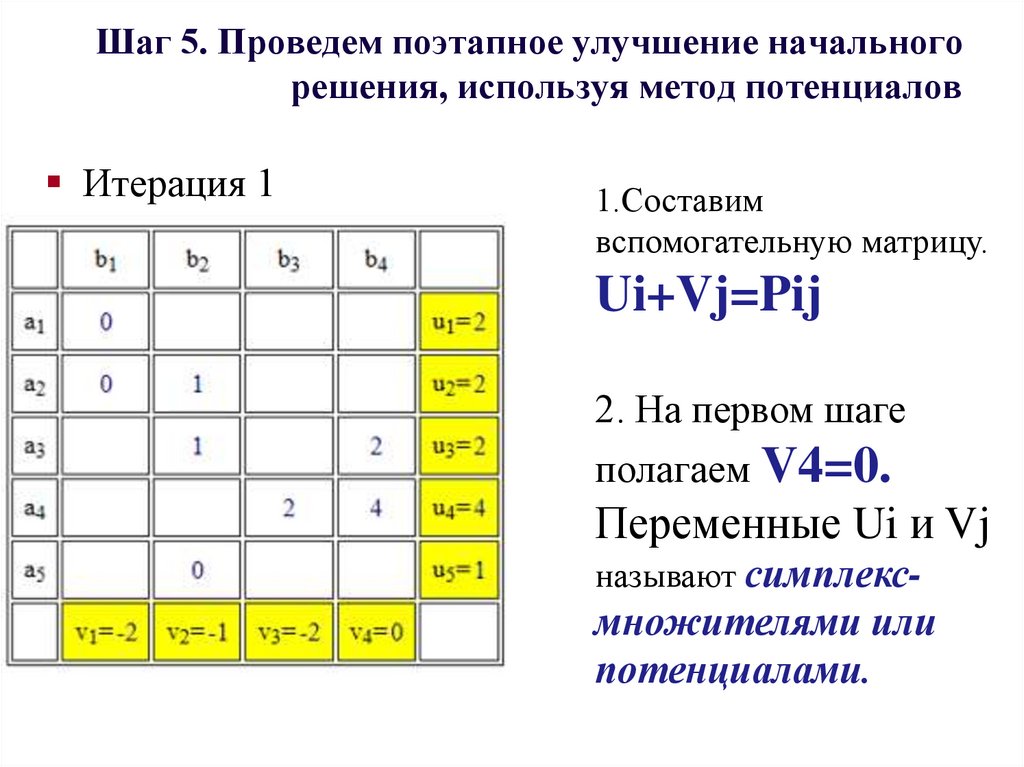
Итерация 11.Составим
вспомогательную матрицу.
Ui+Vj=Pij
2. На первом шаге
полагаем V4=0.
Переменные Ui и Vj
называют симплекс-
множителями или
потенциалами.
36. Шаг 5. Проведем поэтапное улучшение начального решения, используя метод потенциалов
Итерация 1Для всех свободных клеток
рабочей матрицы
вычисляем оценки Sij, по
формуле
Sij=Pij-Ui-Vj
(зеленый цвет)
Если среди оценок есть
отрицательные, то данный
переместив в
соответствующую клетку
некоторое количество товара.
Если отрицательных оценок
нет – план оптимальный.
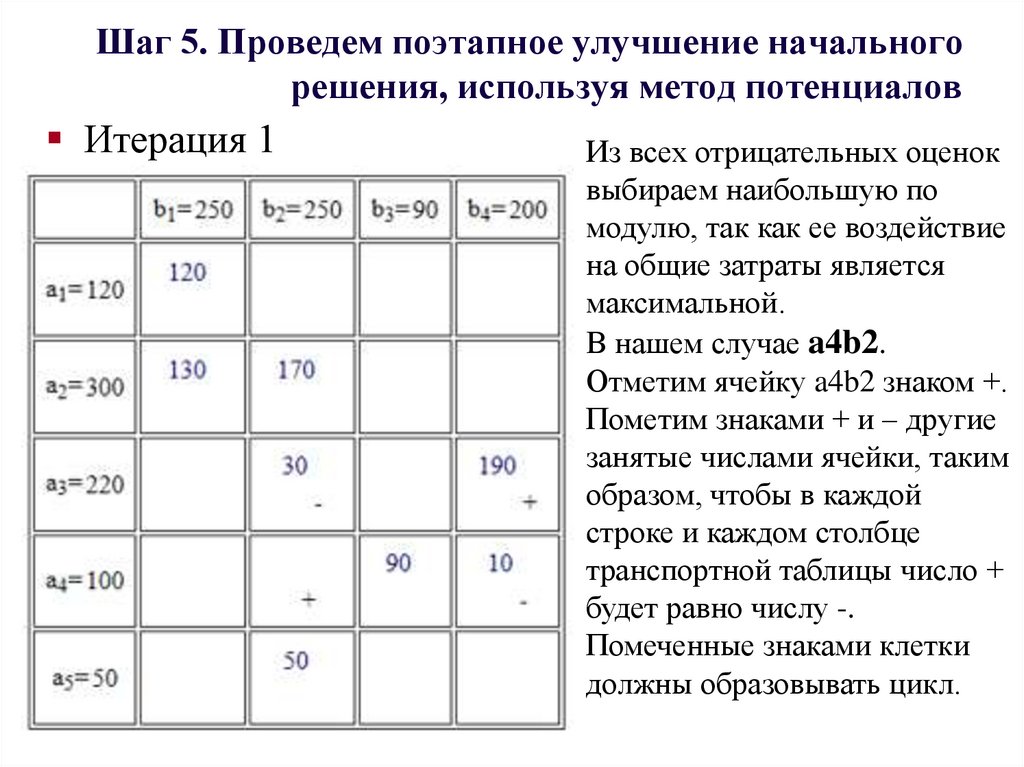
37. Шаг 5. Проведем поэтапное улучшение начального решения, используя метод потенциалов
Итерация 1Из всех отрицательных
оценок выбираем
наибольшую по модулю,
так как ее воздействие на
общие затраты является
максимальной.
В нашем случае a4b2
38. Шаг 5. Проведем поэтапное улучшение начального решения, используя метод потенциалов
Итерация 1Из всех отрицательных оценок
выбираем наибольшую по
модулю, так как ее воздействие
на общие затраты является
максимальной.
В нашем случае a4b2.
Отметим ячейку a4b2 знаком +.
Пометим знаками + и – другие
занятые числами ячейки, таким
образом, чтобы в каждой
строке и каждом столбце
транспортной таблицы число +
будет равно числу -.
Помеченные знаками клетки
должны образовывать цикл.
39. Шаг 5. Проведем поэтапное улучшение начального решения, используя метод потенциалов
Итерация 1Определим минимум М из всех
элементов, помеченных знаком -,
выбираем ячейку где минимум
достигается.
В нашем случае a4b4 и
обозначаем загруженную
клетку, которая должна быть
свободной.
М=10.
Переходим к новой
транспортной таблице.
В ячейку a4b2 =М, ячейка a4b4
остается пустой, в остальных
ячейках, помеченных + или - ,
число М складывается с числом
стоящим в ячейке или вычитается.
40. Шаг 5. Проведем поэтапное улучшение начального решения, используя метод потенциалов
Итерация 1Новая транспортная таблица..
41. Шаг 5. Проведем поэтапное улучшение начального решения, используя метод потенциалов
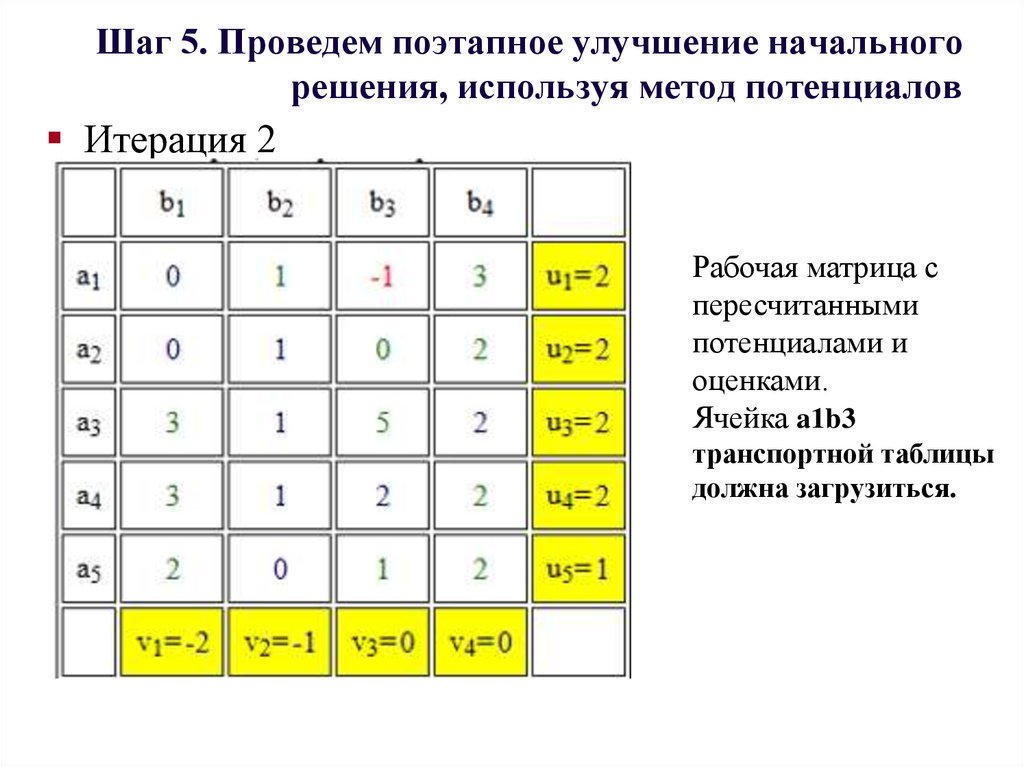
Итерация 2Рабочая матрица с
пересчитанными
потенциалами и
оценками.
Ячейка a1b3
транспортной таблицы
должна загрузиться.
42. Шаг 5. Проведем поэтапное улучшение начального решения, используя метод потенциалов
Итерация 2Ячейка a4b3становится
свободной.
М=90
43. Шаг 5. Проведем поэтапное улучшение начального решения, используя метод потенциалов
Итерация 2Ячейка a4b3становится
свободной.
М=90
44. Шаг 5. Проведем поэтапное улучшение начального решения, используя метод потенциалов
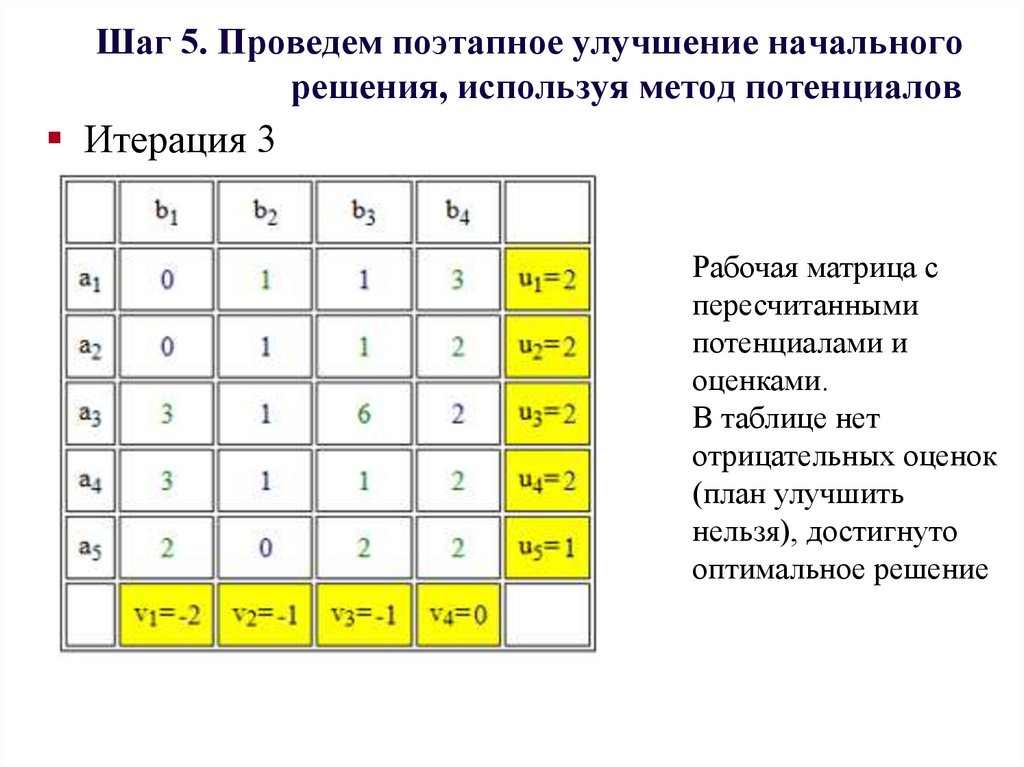
Итерация 3Рабочая матрица с
пересчитанными
потенциалами и
оценками.
В таблице нет
отрицательных оценок
(план улучшить
нельзя), достигнуто
оптимальное решение
45. 6. Задача о назначениях
Имеется n работ и n кандидатов для их выполнения.Затраты i-го кандидата на
выполнение j-й работы равны cij (i; j =1,n) .
Каждый кандидат может быть назначен
только на одну работу, и каждая работа может быть
выполнена только одним кандидатом.
Требуется найти назначение кандидатов на
работы, при котором суммарные затраты на
выполнение работ минимальны.
46. 6. Задача о назначениях
Пусть x ij – переменная, значение которой равно 1, если i-й кандидатвыполняет j-ю работу, и 0 – в противном случае.
Тогда условие о том, что каждый кандидат выполняет только одну
работу, запишется в виде
Условие о том, что каждая работа может выполняться
одним кандидатом, запишется в виде
Целевая функция задачи имеет вид
В функцию входят только те значения c ij (i =1,n; j =1,n),
для которых x ij отличны от 0, т.е. входят затраты,
соответствующие назначенным работам.















































 Информатика
Информатика Менеджмент
Менеджмент








