Похожие презентации:
Шар и сфера
1.
2.
Учебник геометрии Погорелов А.В., §58-61, стр. 96-99Составить конспект по вопросам:
1. Определение шара. Его центр, радиус
2. Шаровая поверхность
3. Диаметр
4. Теорема 6.3 (без доказательства)
5. Диаметральная плоскость, большой
круг, большая окружность
6. Теорема 6.4 (без доказательства)
7. Касательная плоскость и теорема 6.5
(без доказательства)
https://resh.edu.ru/subject/lesson/4034/main/22795/
3.
Шар илисфера?
4.
Шар илисфера?
5.
Шар илисфера?
6.
Шар илисфера?
7.
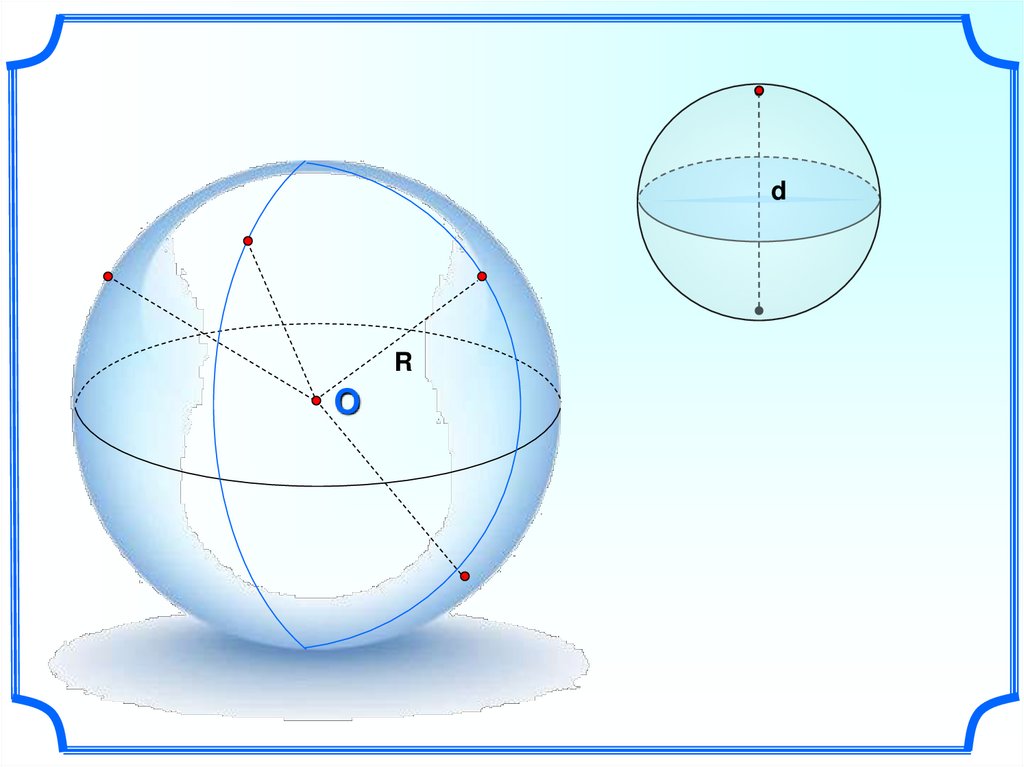
dR
O
8.
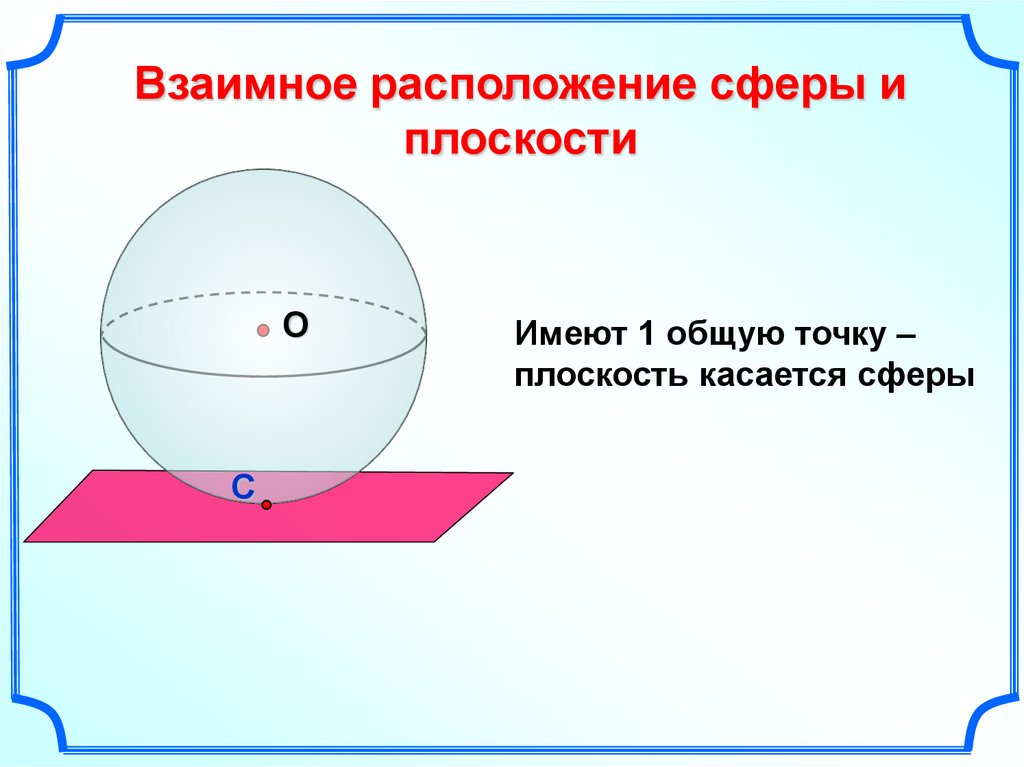
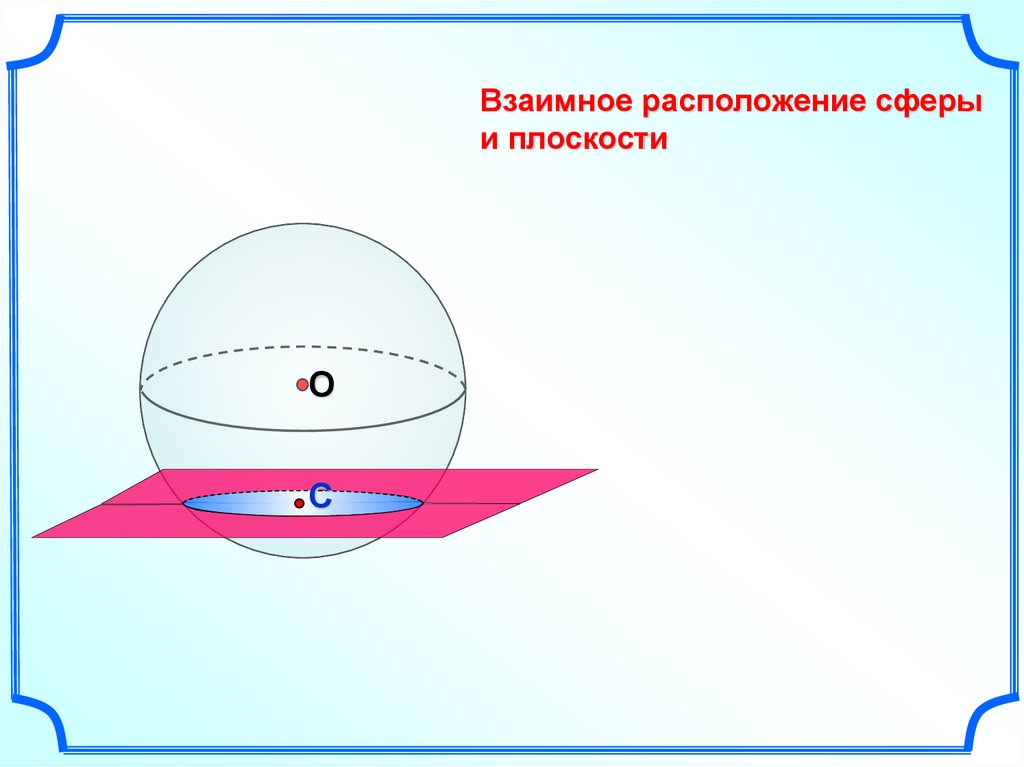
Взаимное расположение сферы иплоскости
О
С
Имеют 1 общую точку –
плоскость касается сферы
9.
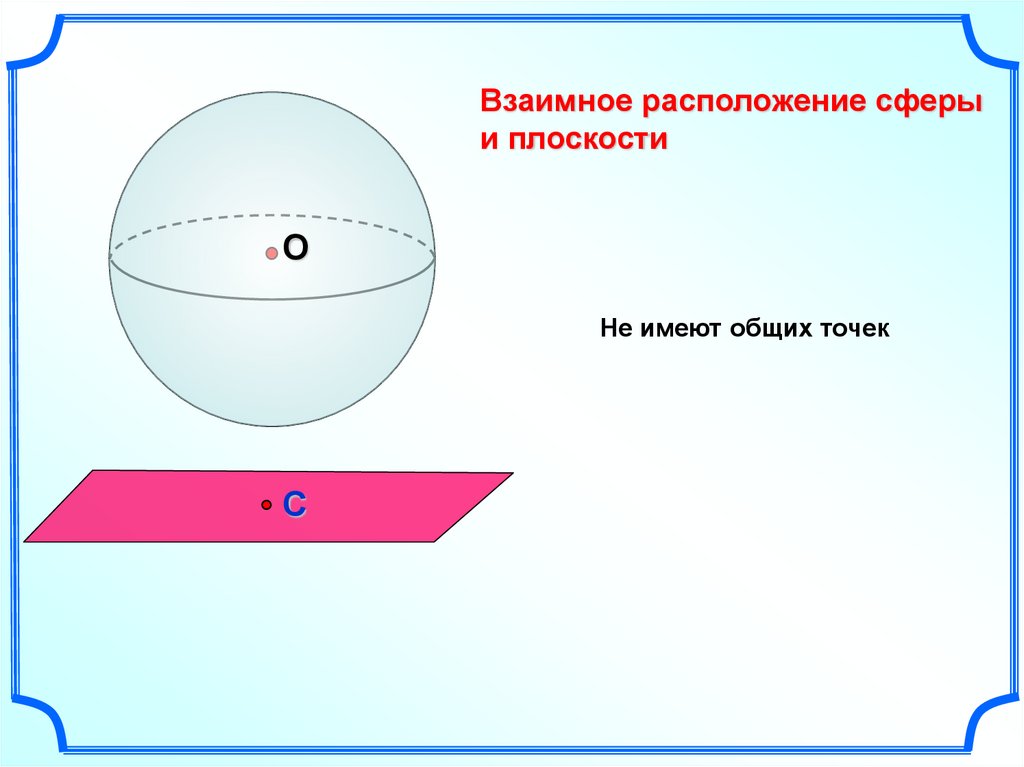
Взаимное расположение сферыи плоскости
О
Не имеют общих точек
С
10.
Взаимное расположение сферыи плоскости
О
С
11.
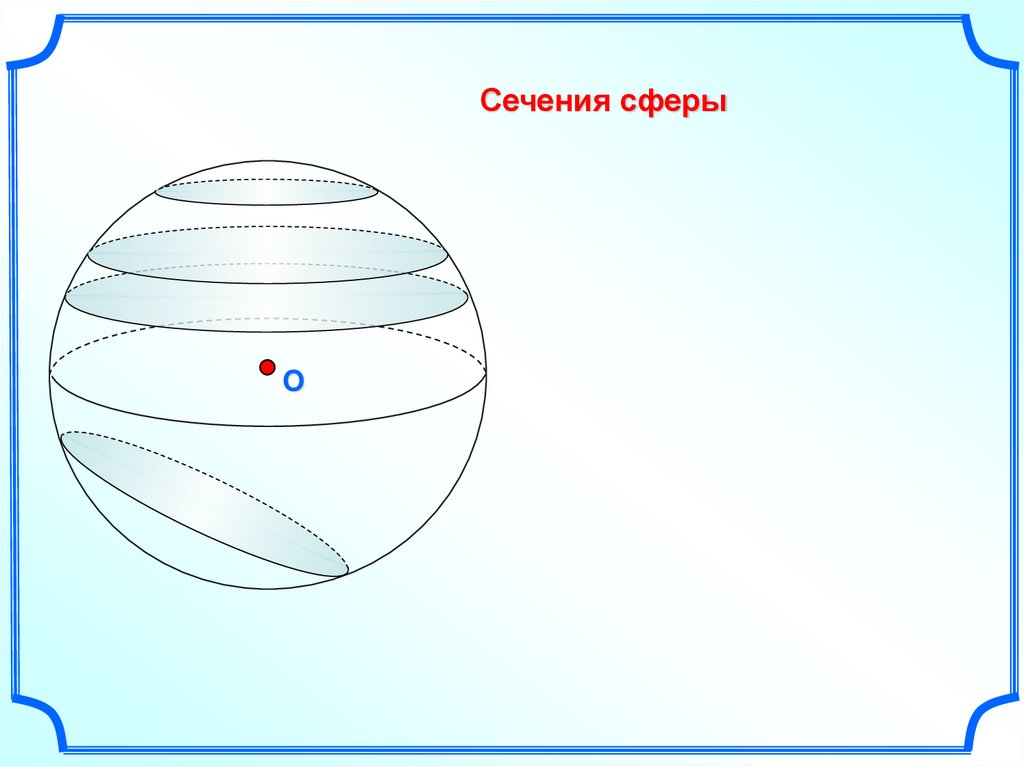
Сечения сферыO
12.
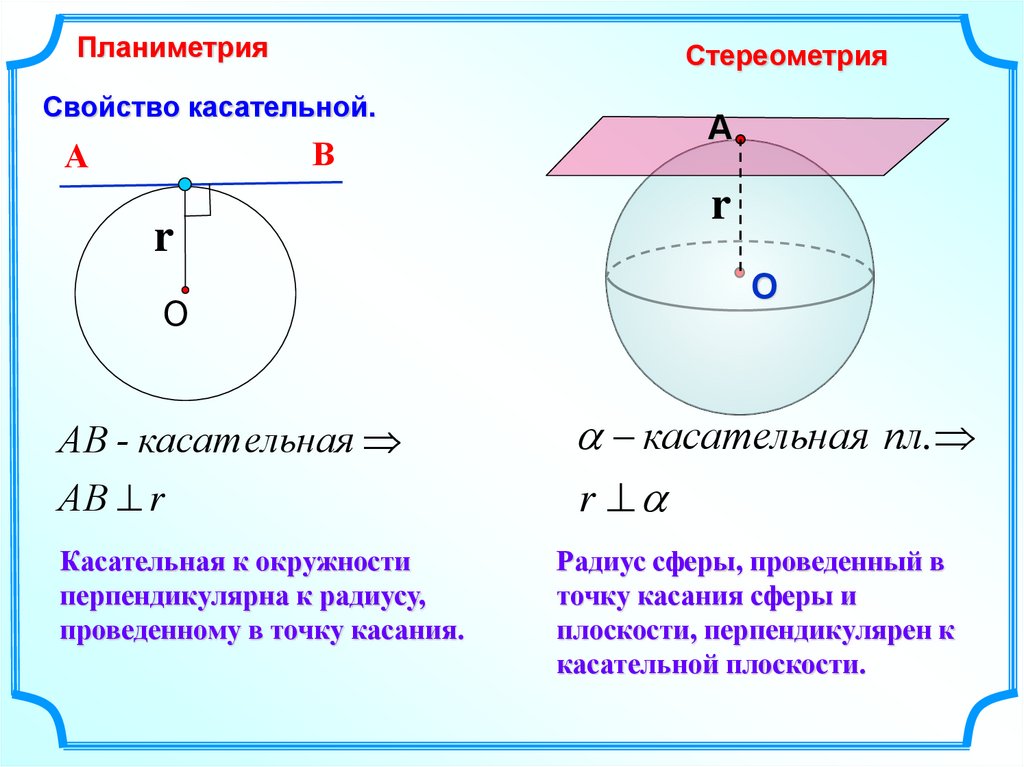
ПланиметрияСтереометрия
Свойство касательной.
В
А
r
О
А
r
О
АВ - касат ельная
АВ r
касательная пл.
r
Касательная к окружности
перпендикулярна к радиусу,
проведенному в точку касания.
Радиус сферы, проведенный в
точку касания сферы и
плоскости, перпендикулярен к
касательной плоскости.
13.
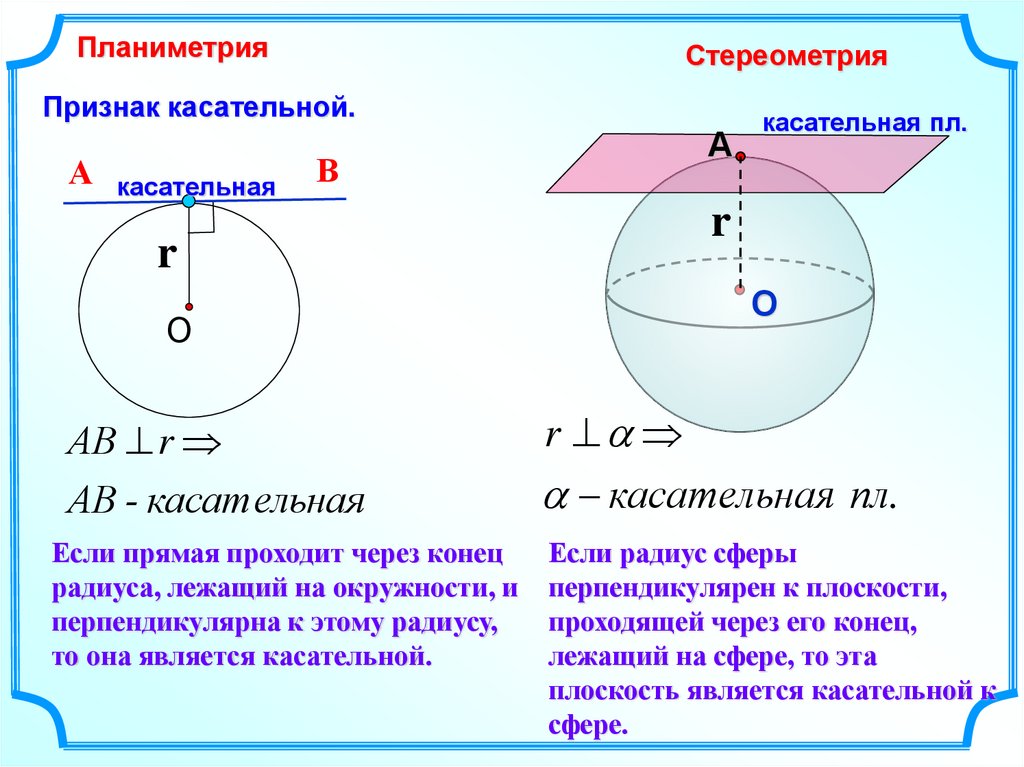
ПланиметрияСтереометрия
Признак касательной.
А касательная
В
r
О
А
касательная пл.
r
О
АВ r
АВ - касат ельная
r
касательная пл.
Если прямая проходит через конец
радиуса, лежащий на окружности, и
перпендикулярна к этому радиусу,
то она является касательной.
Если радиус сферы
перпендикулярен к плоскости,
проходящей через его конец,
лежащий на сфере, то эта
плоскость является касательной к
сфере.
14.
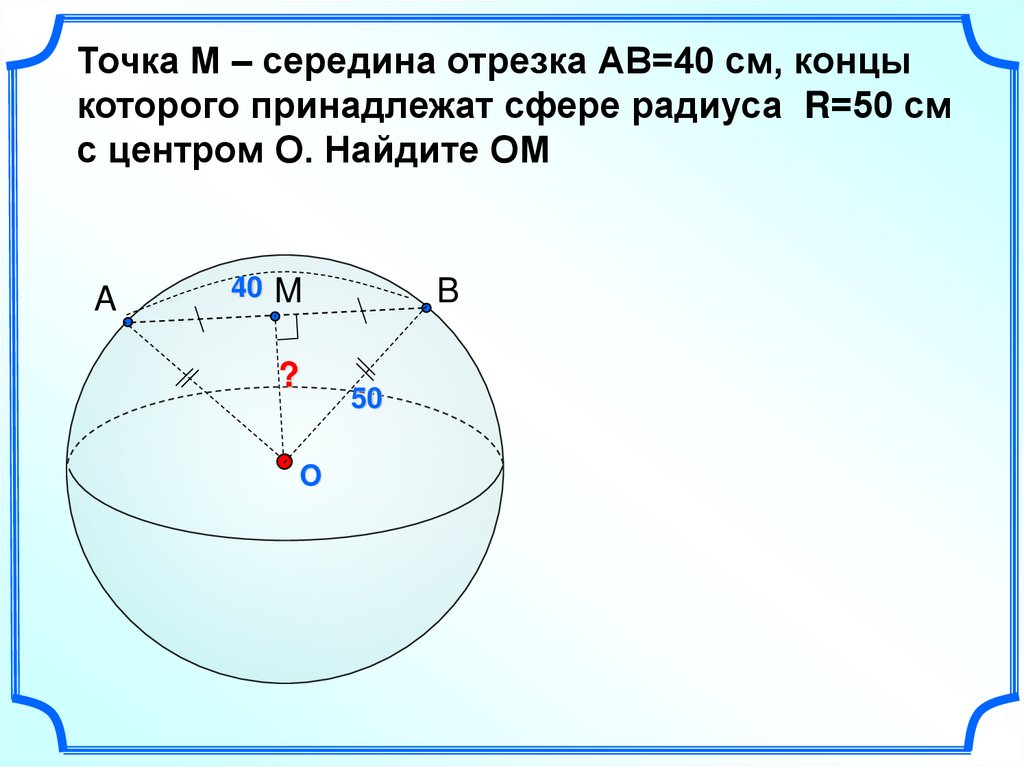
Точка М – середина отрезка АВ=40 см, концыкоторого принадлежат сфере радиуса R=50 см
с центром О. Найдите ОМ
A
40 M
?
B
50
O
15.
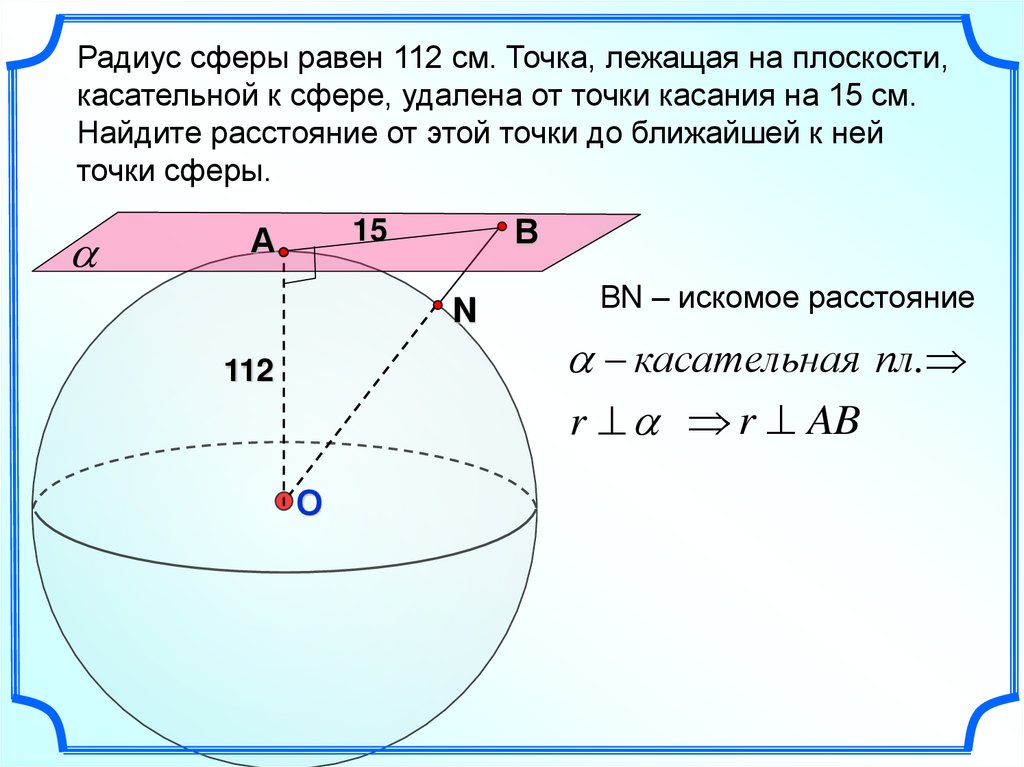
Радиус сферы равен 112 см. Точка, лежащая на плоскости,касательной к сфере, удалена от точки касания на 15 см.
Найдите расстояние от этой точки до ближайшей к ней
точки сферы.
В
15
А
N
112
О
ВN – искомое расстояние
касательная пл.
r r AB
16.
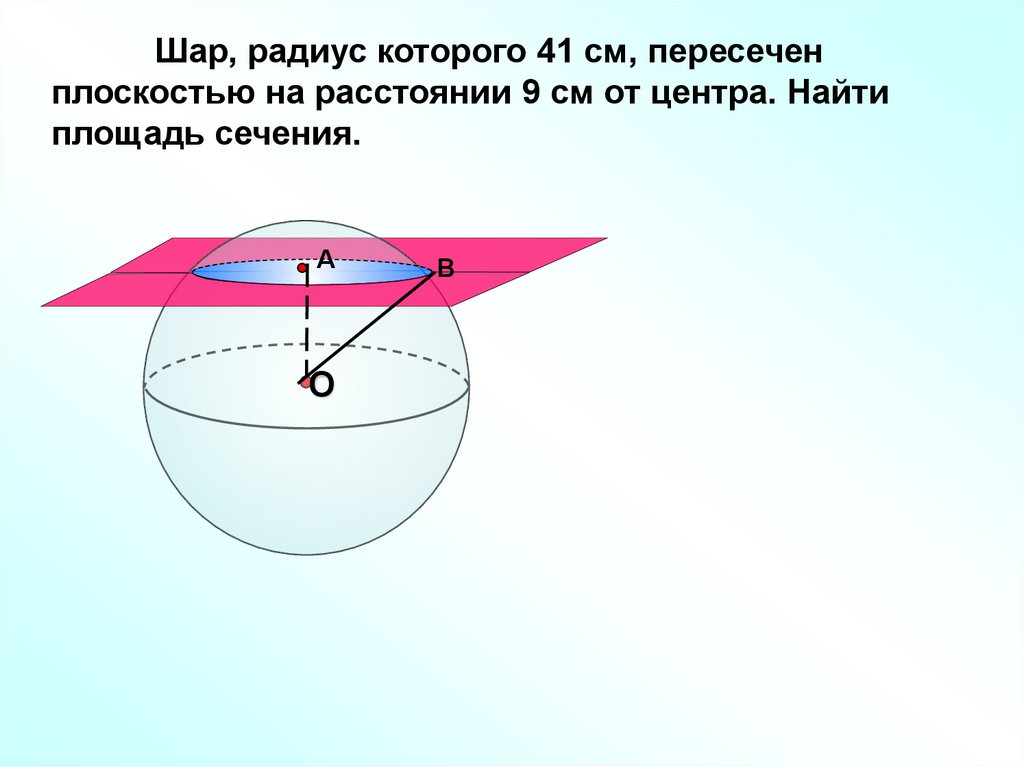
Шар, радиус которого 41 см, пересеченплоскостью на расстоянии 9 см от центра. Найти
площадь сечения.
А
О
В
17.
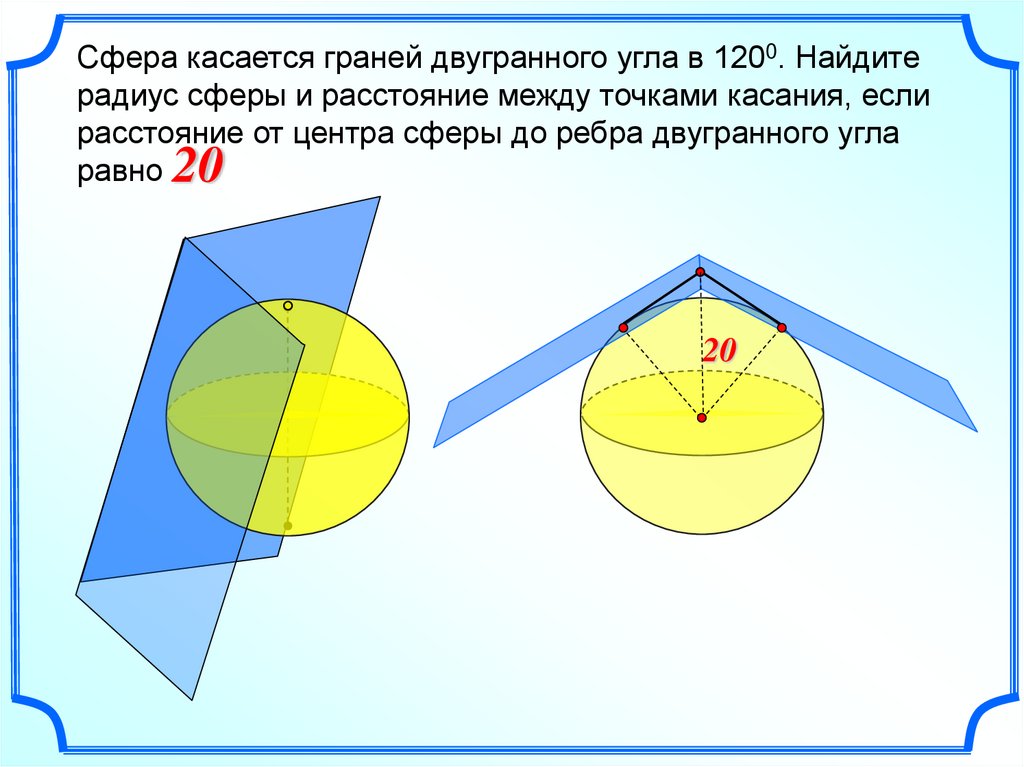
Сфера касается граней двугранного угла в 1200. Найдитерадиус сферы и расстояние между точками касания, если
расстояние от центра сферы до ребра двугранного угла
равно .
20
20
18.
1. Радиусы двух шаров равны 10 и 25. Найдите радиус шара,площадь поверхности которого равна сумме площадей их
поверхностей.
1. К задаче сделать чертеж. Около шара описан цилиндр,
площадь поверхности которого равна 120. Найдите площадь
поверхности шара.
19.
1. Найдите площадь сферы, радиус которой равен: а) 6 см; б) 2 дм;2. Площадь сечения сферы, проходящего через ее центр, равна 9 м2.
Найдите площадь сферы.
3. Площадь сферы равна 324 см2. Найдите радиус сферы.
4. Вычислите радиус круга, площадь которого равна площади сферы радиуса 5 м.
5.







 Математика
Математика








