Похожие презентации:
Молекулярно-кинетические свойства
1.
Молекулярно-кинетические свойстваОтражают молекулярные свойства, обусловленные кинетической
энергией движения частиц и молекул (тепловым движением).
Диффузия
Броуновское движение
Осмос
Седиментационное равновесие
Седиментационный анализ
2. Диффузия
В основе диффузии лежит градиент концентраций. Скорость диффузии тем меньше, чембольше размеры диффундирующих частиц.
Коэффициент диффузии D на 3-5 порядков ниже чем у молекул и ионов (D=10-5 см2/с– у
ионов, молекул; D=10-7 -10-9 см2/с – у коллоидных частиц).
Диффузия зависит:
От размеров частиц дисперсной фазы (с увеличением размеров частиц скорость
диффузии уменьшается).
С. 173-178
От свойств дисперсионной среды (в газе D выше, чем в жидкостях и твердых телах).
От температуры (с повышением температуры D увеличивается).
4 3
r N A
3
Применение:
Дубление кожи
Адгезия, адсорбция материалов, сварка, паяние.
Всасывание продуктов питания в организм.
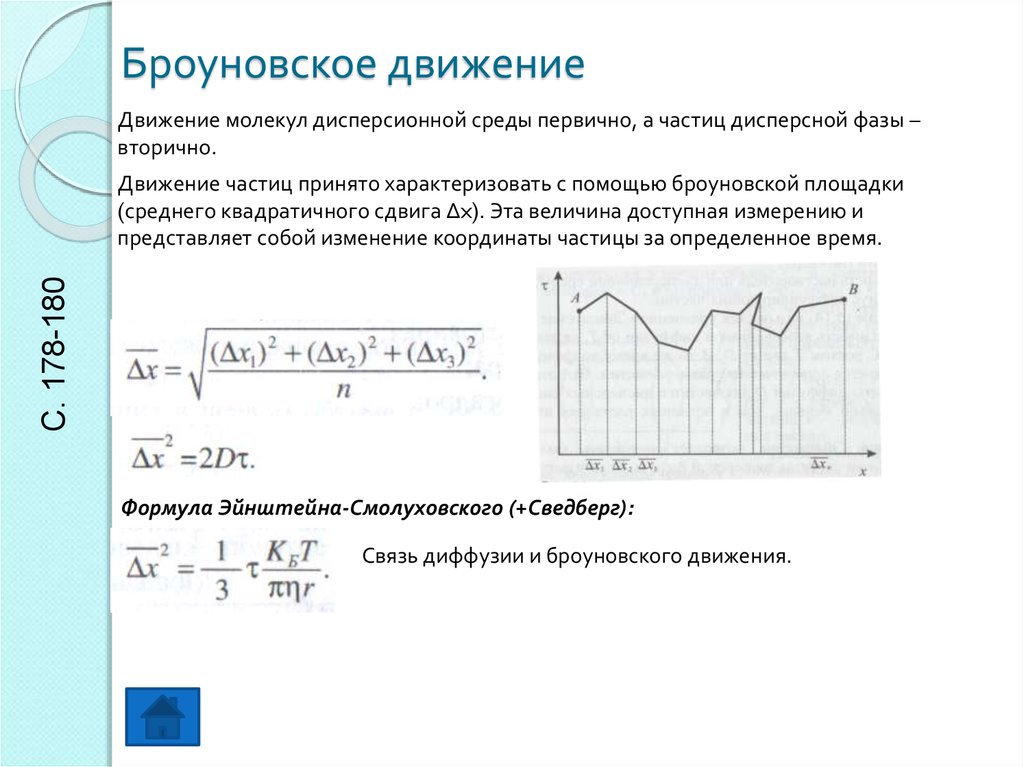
3. Броуновское движение
Движение молекул дисперсионной среды первично, а частиц дисперсной фазы –вторично.
С. 178-180
Движение частиц принято характеризовать с помощью броуновской площадки
(среднего квадратичного сдвига Δx). Эта величина доступная измерению и
представляет собой изменение координаты частицы за определенное время.
Формула Эйнштейна-Смолуховского (+Сведберг):
Связь диффузии и броуновского движения.
4. Осмос
С. 173-175Движение растворителя через полупроницаемую перегородку (мембрану) из
растворителя в раствор (или из разбавленного раствора в концентрированный), т.е. из
раствора меньшей концентрации в раствор с большей концентрацией.
Обычно движущей силой осмоса считают разность химических потенциалов
растворителя в чистом растворителе и в растворе:
Применение:
Мембранные технологии очистки
В основе лежит способность частиц и макромолекул не проходить через
полупроницаемую мембрану (низкомолекулярные ионы и молекулы(малые размеры
пор)).
5. Седиментационное равновесие
С. 180-189Седиментацией называется осаждение частиц под действием силы тяжести.
Оценить седиментационную или кинетическую устойчивость дисперсной
системы можно сравнивая поток диффузии jD и противодействующий ему
поток седиментации jS .
- седиментационно-диффузионное равновесие
6.
Седиментация - оседание частиц под действием сил тяжестиДиффузия частиц – перемещение частиц из слоя , где их концентрация
больше в слой, где концентрация меньше.
Vсед.
х1
2 g ( 1 0 ) r 2
9
RT
D
6 rN A
с1
1.
х2
Vдиф.
dc
D
dx
Vсед . Vдиф.
осадок
с2
2.
Vдиф. Vсед .
частицы равномерно распределены
по всему объёму дисперсионной
среды
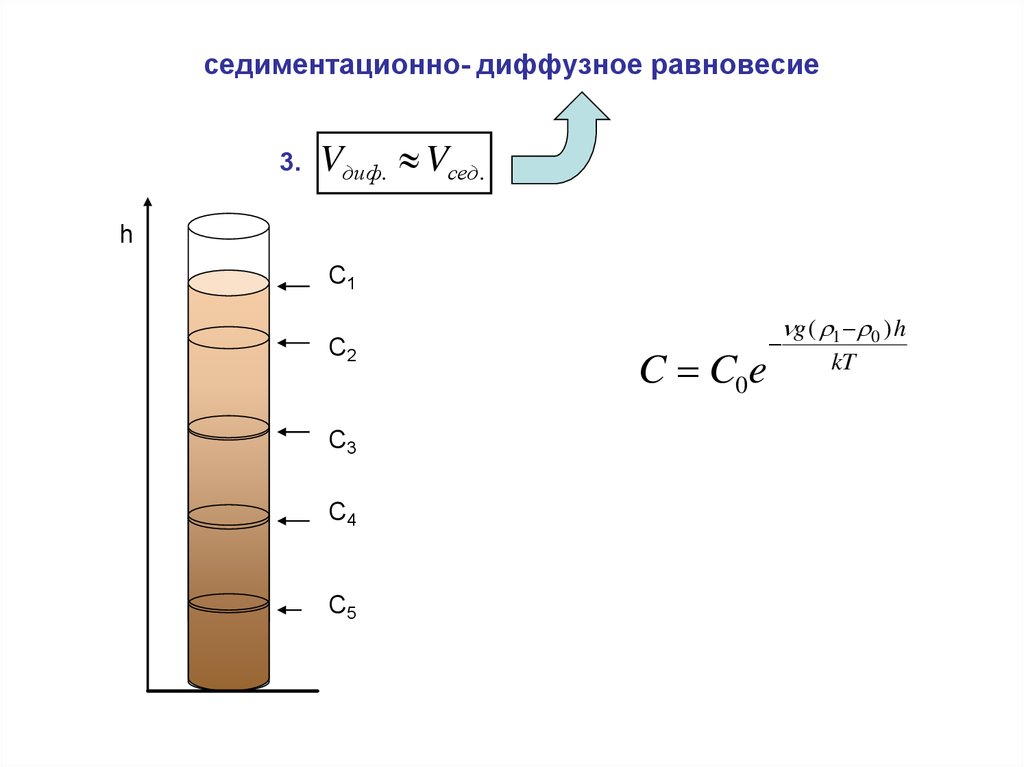
7.
седиментационно- диффузное равновесие3.
Vдиф. Vсед .
h
С1
С2
С3
С4
С5
C C0e
g ( 1 0 ) h
kT
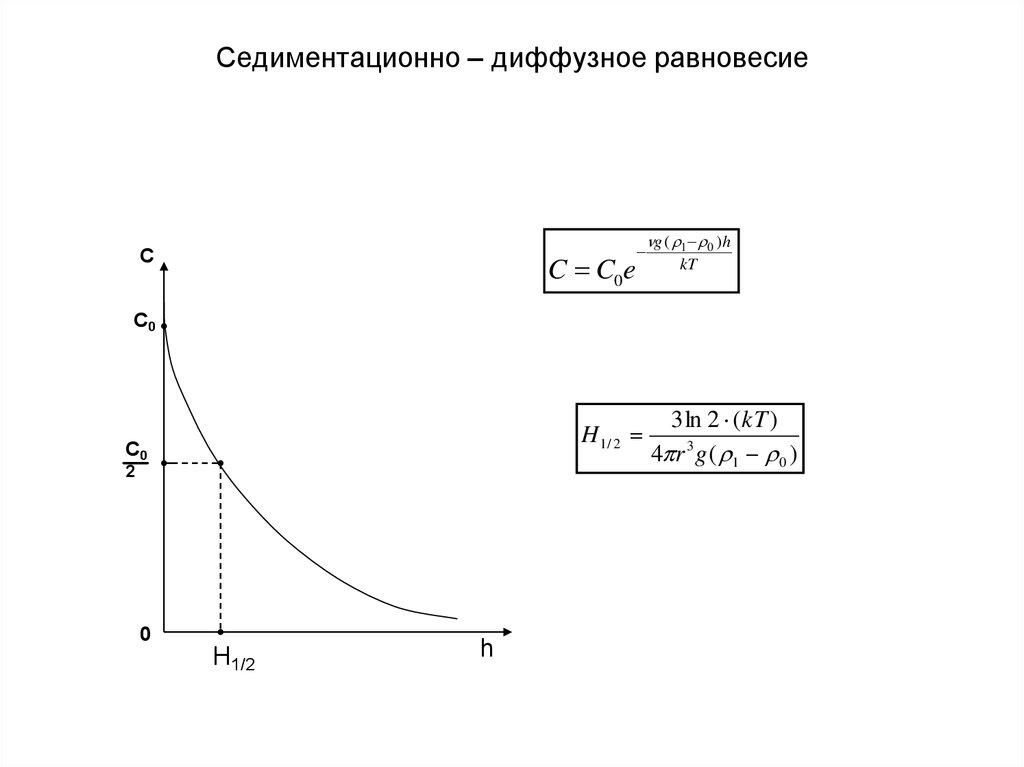
8.
Седиментационно – диффузное равновесиеC
C C0e
g ( 1 0 ) h
kT
C0
H1/ 2
C0
2
0
H1/2
h
3 ln 2 ( kT )
4 r 3 g ( 1 0 )
9. Седиментационный анализ
P=f – Закон Стокса.- сила вязкого сопротивления среды.
С. 182-196
- сила осаждения частицы шарообразной формы.
- закон Стокса для шарообразной частицы.
- выражение для радиуса r частицы.
- константа седиментации.
- выражение для радиуса r частицы через высоту столба суспензии
H и время полного осаждения частиц t.
10.
Оптические свойстваС. 197-211
Оптические свойства зависят от размеров частиц. Для средне- и
грубо дисперсных возможно рассеяние света, преломление,
отражение и поглощение света. В высокодисперсных – только
рассеяние (опалесценция).
Рассеяние света
Поглощение света
Оптические методы анализа
11. Рассеяние света в дисперсных системах
Эффект Тиндаля: дисперсная системасодержит мелкие взвешенные частицы
дисперсной фазы, показатель преломления
которой отличается от показателя преломления
дисперсионной среды.
2
24 π V ν n12 -n 02
Ip =K I0 =
2
I0
4
2
λ
n1 +2n 0
3
2
-уравнение Релея для сферических и
непроводящих частиц
-весовая концентрация
-уравнение Релея
12. Рассеяние света в дисперсных системах
м2
13. Поглощение света
Поглощение света - это явление индивидуальное и селективное. Индивидуальноепотому, что оно зависит от химических свойств данного вещества, а селективное потому,
что всякая система поглощает только определенную часть спектра, то есть свет
определенной длины волны.
В любой дисперсной системе имеются два поглощающих вещества: дисперсная фаза и
дисперсионная среда.
закон Ламберта Бера
-закон Ламберта Бера ( в системах с проводящими частицами)
- мутность
-связь между оптической плотностью D и мутностью t
14. Оптические методы анализа
Светорассеяние лежит в основе оптических методов анализа дисперсныхсистем. Это наиболее распространенные методы исследования концентрации,
размера, формы и структуры дисперсной фазы. Эти методы незаменимы для
получения информации о быстропротекающих процессах без отбора пробы и
химическою анализа.
Делятся оптические методы анализа на:
Нефелометрия
Турбидиметрия
Ультрамикроскопия
15. Нефелометрия
Нефелометрия (от греческого слова "nefo" облако) основана на использованииуравнения Релея:
Для стандартного раствора:
Для исследуемого раствора:
=>
=>
или
При условии равенства концентраций:
=>
r
3
3V
4
=>
=>
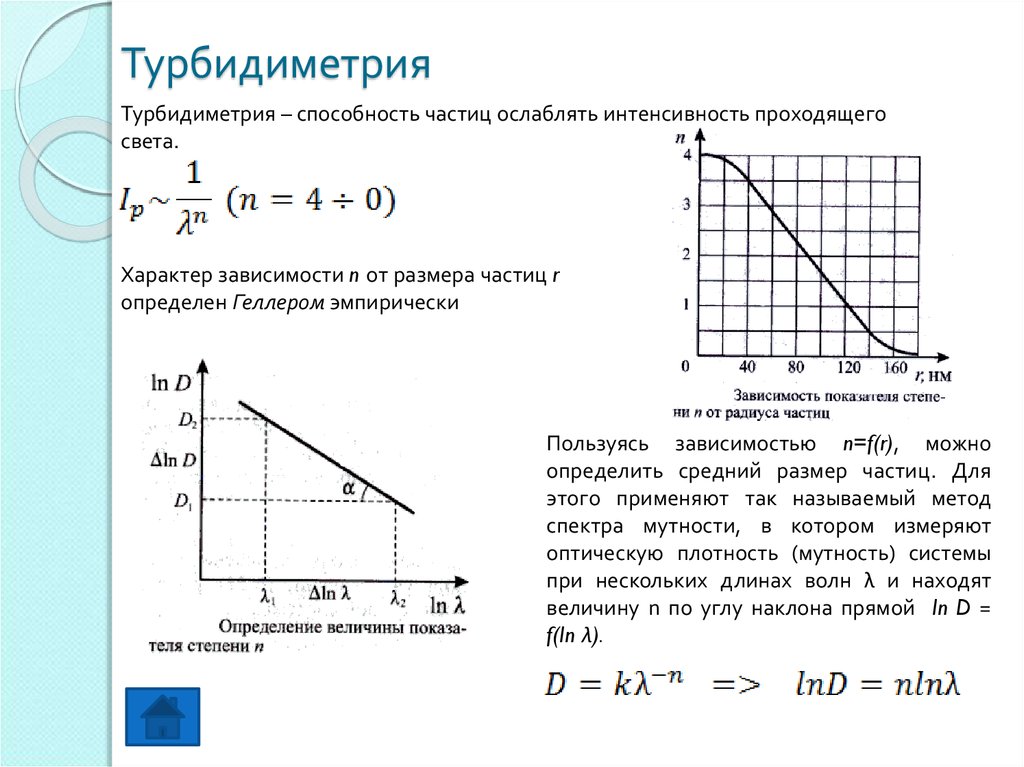
16. Турбидиметрия
Турбидиметрия – способность частиц ослаблять интенсивность проходящегосвета.
Характер зависимости n от размера частиц r
определен Геллером эмпирически
Пользуясь зависимостью n=f(r), можно
определить средний размер частиц. Для
этого применяют так называемый метод
спектра мутности, в котором измеряют
оптическую плотность (мутность) системы
при нескольких длинах волн λ и находят
величину n по углу наклона прямой In D =
f(In λ).
17. Ультрамикроскопия
Ультрамикроскопия – определение наличия частиц, их размеров и концентрации прирассмотрении дисперсной системы под микроскопом.
Для определения размеров частиц поступают следующим образом: в поле зрения
окуляра подсчитывают число светящихся точек. Подсчет ведут несколько раз. так как
число частиц в поле зрения меняется. Находят среднее число частиц n. Объем раствора V
представляет собой константу прибора и определяется как произведение площади
окуляра на глубину поля зрения.
- вес одной частицы
- вес одной частицы (шарообразной)
-размер частицы
-постоянная величина
18.
Структурно-механические свойства дисперсных системЭто комплекс механических свойств (вязкость, пластичность, упругость,
прочность), связанных с образованием структуры. Структурообразование
это вариант коагуляции при большой концентрации д.ф.
Изучением связи структуры и механических свойств занимается
физико-химическая механика (П.А.Ребиндер)
Изучаются механические свойства по проявлению деформации под
действием внешних напряжений (методами реологии) – науки о
деформации и течении.
19.
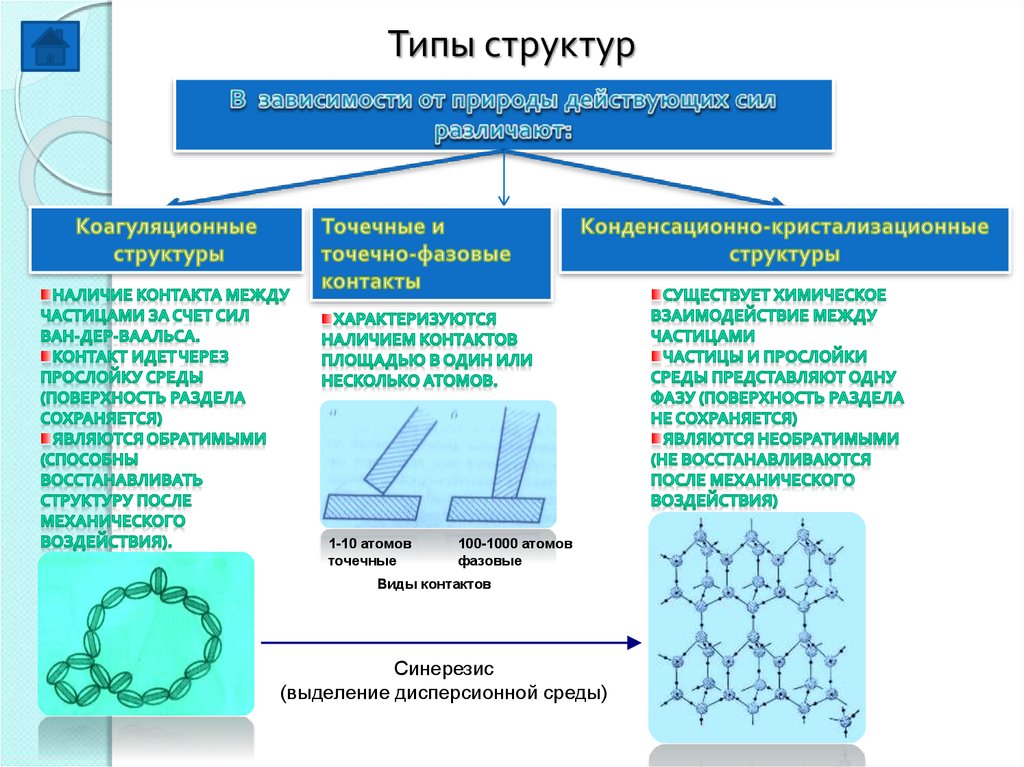
Типы структур1-10 атомов
точечные
100-1000 атомов
фазовые
Виды контактов
Синерезис
(выделение дисперсионной среды)
20.
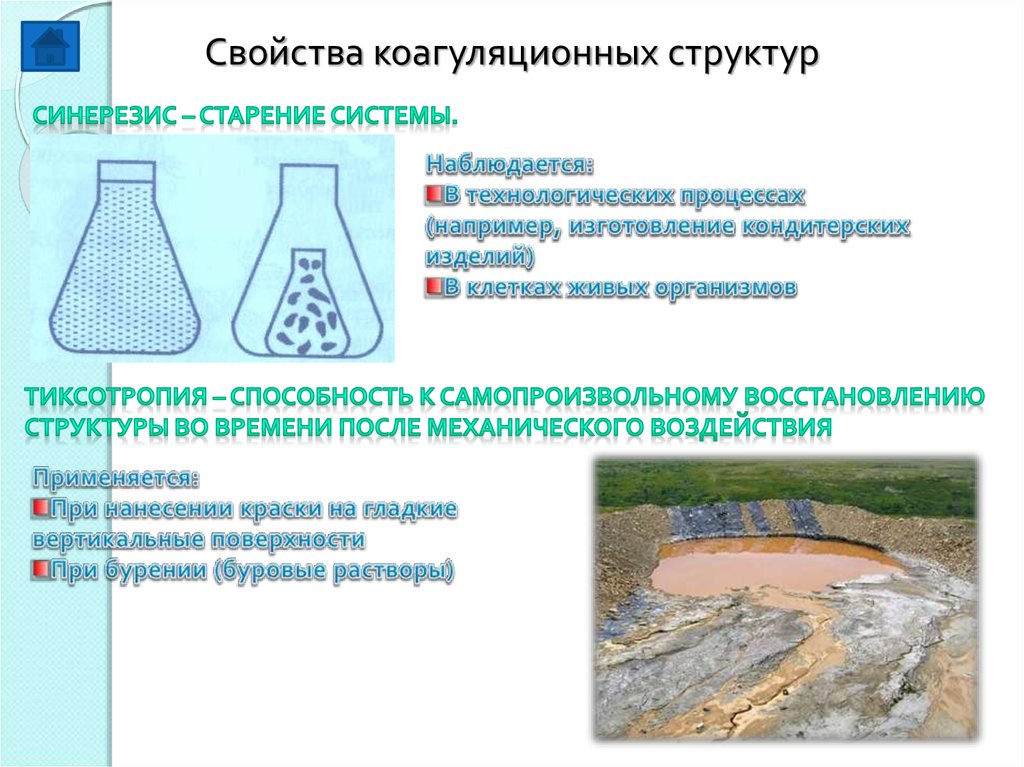
Свойства коагуляционных структур21.
Изучение (реологические свойства)Все виды деформации (кручение, растяжение, сжатие) можно
свести к основному виду – деформации сдвига γ под действием
н
напряжения сдвига р 2 Па
м
Реология изучает связь γ и р или скорости деформации
Все системы можно условно разделить на бесструктурные
(Ньютоновские) и структурированные (Неньютоновские).
d
и р.
d
22.
Ньютоновские (бесструктурные) системыПодчиняются законам Ньютона, Пуазейля и Энштейна.
1
1
р
Q
, где K
const
1
2
1
tg
1
1
Закон Пуазейля
K p
2
F
р
m
a
1
1 2
р
р
2
r4
K p const
8 l
tg
1
K
р
2 1
р
23.
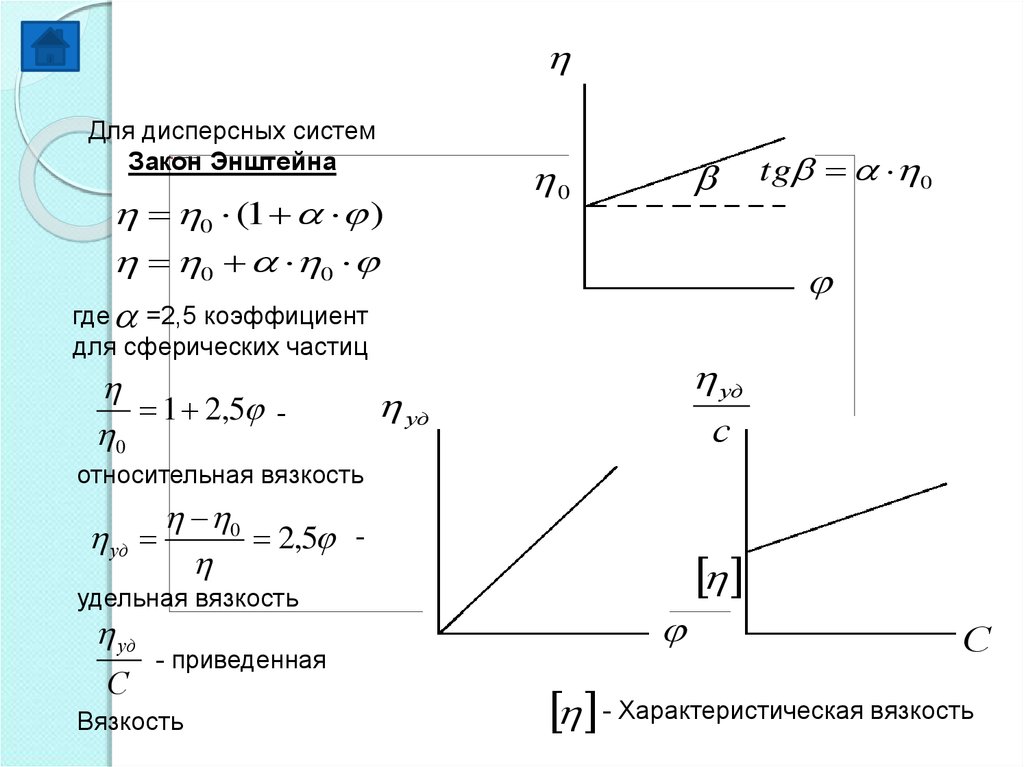
Для дисперсных системЗакон Энштейна
0 (1 )
0 0
0
где =2,5 коэффициент
для сферических частиц
1 2,5
0
уд
уд
-
tg 0
с
относительная вязкость
0
уд
2,5
удельная вязкость
уд
С
- приведенная
Вязкость
-
С
- Характеристическая вязкость
24.
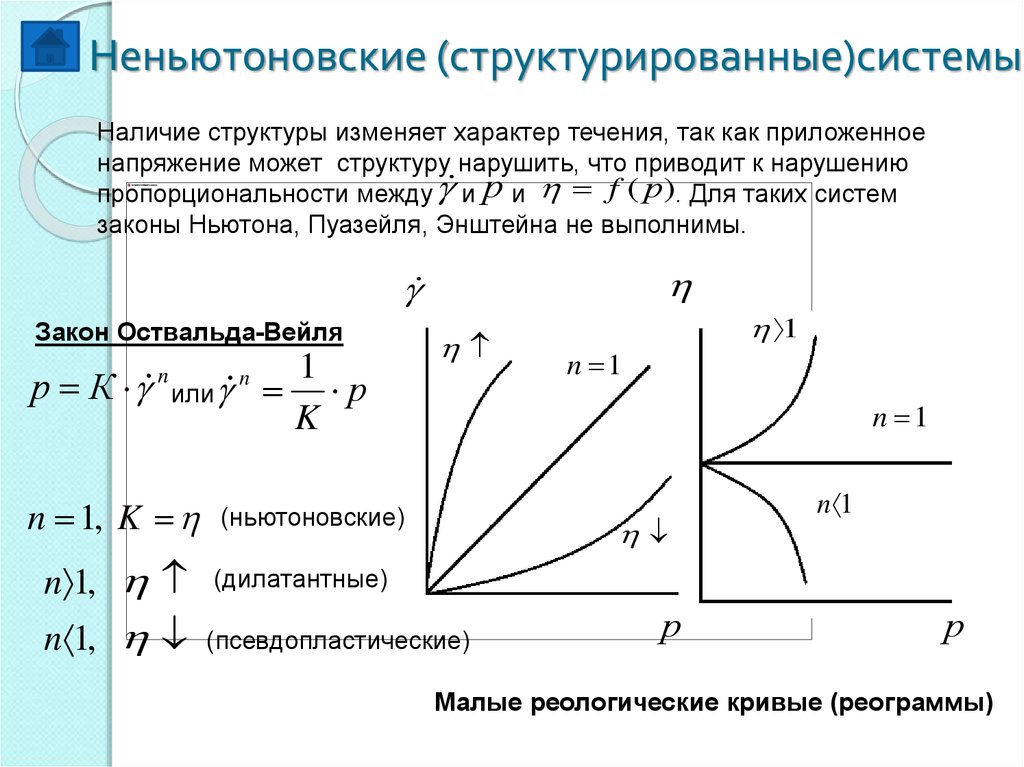
Неньютоновские (структурированные)системыНаличие структуры изменяет характер течения, так как приложенное
напряжение может структуру нарушить, что приводит к нарушению
пропорциональности между и р и f ( р ). Для таких систем
законы Ньютона, Пуазейля, Энштейна не выполнимы.
Закон Оствальда-Вейля
1
р К или р
K
n
n 1, K
n
1
n 1
n 1
(ньютоновские)
n 1,
(дилатантные)
n 1,
(псевдопластические)
р
n 1
р
Малые реологические кривые (реограммы)
25.
Полные реологические кривыеДля АВ
tg 1 max
2
B
tg 2 min
Уравнение Бингама
p pT *
1
*
A
или
( p pT )
1
tg 3 *
рT - Предел текучести
3
р
0
рT
*
- пластическая вязкость
p pT
max
*
Для твердообразных
систем при р=0
течение отсутствует
pT
*
min
0
А
(сдвиговая прочность)
В
-
Общая вязкость
р

















 Химия
Химия








