Похожие презентации:
Формы представления операций алгебры логики
1.
Формы представленияопераций алгебры логики
Презентацию подготовил
Студент группы К-1202
Михаил Корсаков
2.
Алгебра логикиТеоретической основой цифровых устройств, описываемых
логическими функциями, является алгебра логики.
Существуют три способа задания логических функций (ЛФ):
словесное описание;
таблица истинности;
структурная формула.
3.
Словесное описаниеСловесное описание должно однозначно
определять, при каких значениях входных сигналов
функция y принимает значение 1, а при каких – 0.
Так, например, для i = 1, n = 2 имеем следующее
словесное описание:
если x1 = x2 , то y1 = 0, а если x1 ≠ x2 , то y1 = 1.
4.
Таблица истинностиТаблица истинности – перечисление всех
возможных значений входных и соответствующих им
выходных сигналов. При этом способе задания
функция y представляется в виде таблицы, в
которой записываются все возможные наборы
входных сигналов и для каждого набора
устанавливается значение функции (0 или 1).
Таблица истинности представляет собой
табличную форму записи словесного
описания логической функции.
5.
Логическое«НЕ»
Логическое
«ИЛИ»
«Отрицающее ИЛИ»
x
y
x1
x2
y
x1
x2
y
1
0
0
0
0
0
0
0
0
1
0
1
1
0
1
1
1
0
1
1
0
1
1
1
1
1
1
0
Логическое
«И»
Логическое
«И-НЕ»
Логическое
«ИЛИ-НЕ»
x1
x2
y
x1
x2
y
x1
x2
y
0
0
0
0
0
1
0
0
1
0
1
0
0
1
1
0
1
0
1
0
0
1
0
1
1
0
0
1
1
1
1
1
0
1
1
0
6.
Структурная формулаСуществуют две формы записи структурной формулы, дающие
однозначное представление логической функции: в виде
совершенной дизъюнктивной нормальной формы (СДНФ) и в
виде совершенной конъюнктивной нормальной формы (СКНФ).
К свойствам СДНФ следует отнести следующие:
в СДНФ нет двух одинаковых произведений;
ни одно произведение не содержит двух одинаковых множителей;
ни одно произведение не содержит вместе с независимой
переменной её инверсию.
7.
Запись структурной формулы по таблицеистинности в виде СДНФ
Для записи структурной формулы в виде СДНФ по таблице
истинности необходимо:
отметить строки, где y = 1;
для каждой отмеченной строки составить логическое
произведение всех независимых переменных, причём
независимая переменная, равная 1 в выделенной строке, входит
в соответствующее произведение без инверсии, а равная 0 – с
инверсией;
составить логическую сумму полученных произведений.
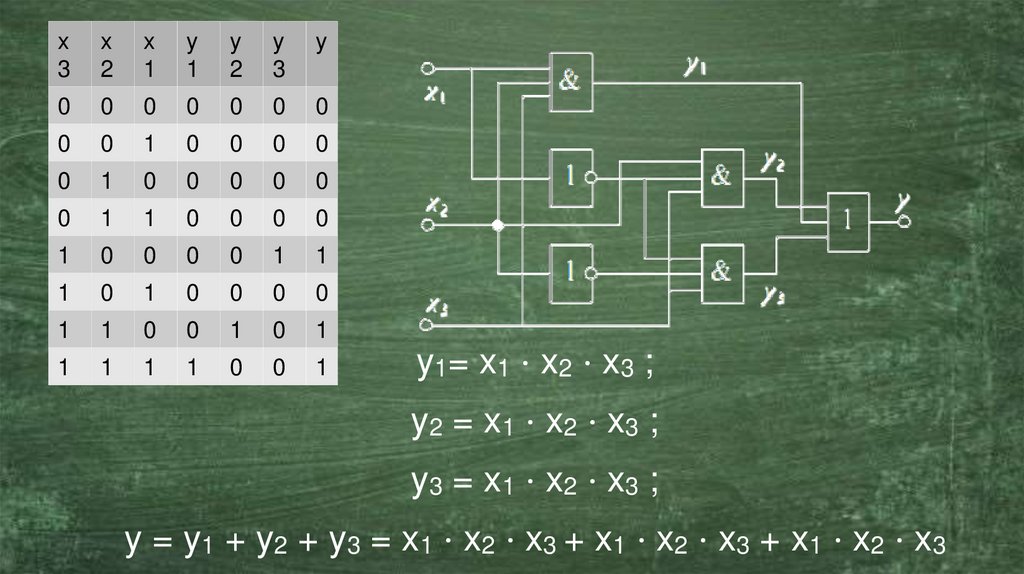
8.
x3
x
2
x
1
y
1
y
2
y
3
y
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
1
0
0
0
0
0
0
1
1
0
0
0
0
1
0
0
0
0
1
1
1
0
1
0
0
0
0
1
1
0
0
1
0
1
1
1
1
1
0
0
1
y 1= x 1 ⋅ x 2 ⋅ x 3 ;
y2 = x 1 ⋅ x2 ⋅ x3 ;
y3 = x 1 ⋅ x2 ⋅ x3 ;
y = y1 + y 2 + y 3 = x 1 ⋅ x 2 ⋅ x 3 + x 1 ⋅ x 2 ⋅ x 3 + x 1 ⋅ x 2 ⋅ x 3
9.
Запись структурной формулы ввиде СКНФ.
Для записи структурной формулы в виде СКНФ по таблице
истинности необходимо:
отметить все строки, где y = 0;
для каждой отмеченной строки составить логическую сумму всех
независимых переменных, причём независимая переменная,
равная 0 в выделенной строке, входит в соответствующую сумму
без инверсии, а равная 1 – с инверсией;
составить логическое произведение полученных сумм.
10.
x3
x
2
x
1
y
1
y
2
y
3
y
0
0
0
0
1
1
0
0
0
1
1
0
1
0
0
1
0
1
1
1
1
0
1
1
1
1
0
0
1
0
0
1
1
1
1
1
0
1
1
1
1
1
1
1
0
1
1
1
1
1
y11= x11 ⋅1x21⋅ x13 ; 1
y2 = x 1 ⋅ x2 ⋅ x3 ;
y3 = x 1 ⋅ x2 ⋅ x3 ;
y = y1 y2 y3 = (x1 ⋅ x2 ⋅ x3)(x1 ⋅ x2 ⋅ x3)(x1 ⋅ x2 ⋅ x3)








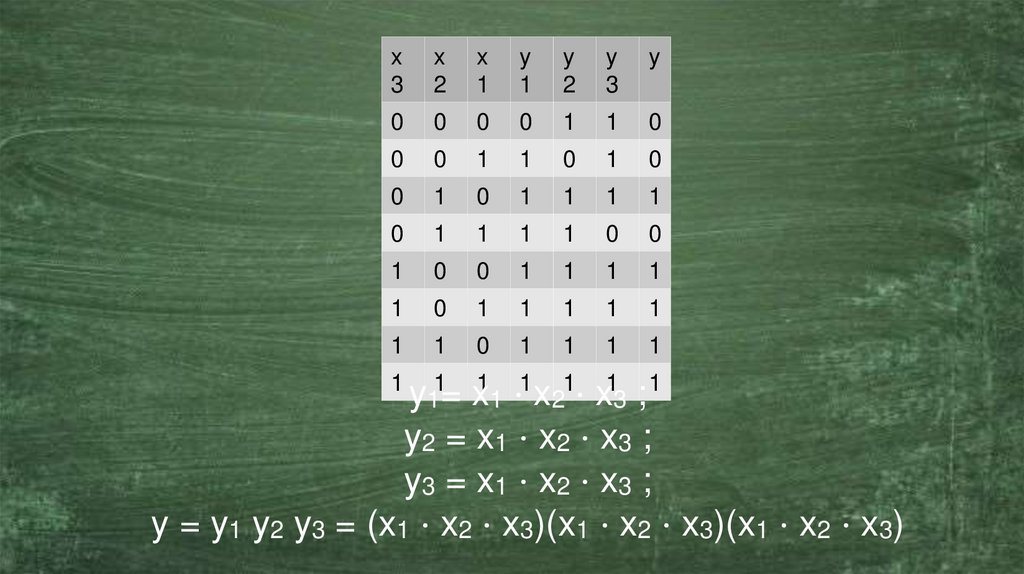

 Математика
Математика








