Похожие презентации:
Системы счисления древнего мира
1. «Системы счисления древнего мира»
Автор: Логунова Софья,Студент 1 курса ИСП-221о
Руководитель: Л.Е. Лукьяненко
2.
• Объект исследования – системы счисления древнего мира.• Целью исследования является изучение истории возникновения
систем счисления и применение систем счисления в жизни.
• Задачи исследования:
• рассмотреть понятие систем счисления и их виды;
• изучить и проанализировать литературу, посвященную системам
счисления;
• рассмотреть применение систем счисления в жизни человека и в
компьютерной технике.
3. Понятие системы счисления
Система счисления – это способ записи чисел с помощью заданного набораспециальных знаков (цифр, букв и т. д.), который называют алфавитом.
Понятие «число» является ключевым как для математики, так и для
информатики. Люди всегда считали и записывали числа, даже 5 тысяч лет
назад. Но записывали их по другим правилам, хотя в любом случае число
изображалось с помощью любого или нескольких символов, которые
назывались цифрами.
4. Примеры непозиционных систем счисления: Египетская система счисления
• У многих народов использовалась система, алфавит которой состоял из одногосимвола – палочки. Египтяне применяли для записи чисел иероглифы. Единицу
обозначали одной вертикальной чертой, а для обозначения чисел, меньших 10, нужно
было поставить соответствующее число вертикальных штрихов. . Если штрихов нужно
изобразить несколько, то их объединяли в группы из трех или четырех черт и
изображали в несколько рядов, причем в нижнем должно быть столько же штрихов
сколько и в верхнем, или на одну больше.
5. Самым распространенным примером непозиционной системы счисления является римская система счисления
• Первая известная нам система, основанная напозиционном принципе – шестидесятeричная вавилонская.
Например, число 59 в данной системе записывается
следующим образом:
, т.е. 59 = 5 · 10 + 9.
6. Позиционные системы счисления.
• Позиционной называется такая система счисления, в которой величина,обозначаемая цифрой в записи числа, зависит от ее позиции.
• Запись чисел в позиционных системах счисления осуществляется
следующим образом: множество цифр, используемых для записи чисел в
позиционных системах счисления, образует алфавит. Количество
используемых цифр называется основанием системы счисления. Место
каждой цифры в числе – позиция.
Основание
Название
Алфавит
(n)
n=2
двоичная
0, 1
n=3
троичная
0, 1, 2
n=5
пятеричная
0, 1, 2, 3, 4
n=8
восьмеричная
0, 1, 2, 3, 4, 5, 6, 7
n=10
десятичная
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
n=16
шестнадцатеричная
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
7. История возникновения систем счисления
Считать человек начал задолго до того, как он научился писать, поэтому не сохранилось никаких письменных документов,свидетельствовавших о тех словах, которыми в древности обозначали числа.
Из этих надписей известно, что древние египтяне использовали только десятичную систему счисления. Единицу
обозначали одной вертикальной чертой, а для обозначения чисел, меньших 10, нужно было поставить соответствующее
число вертикальных штрихов.
Введение египтянами цифровых обозначений ознаменовало один из важных этапов в развитии систем счисления, так как
дало возможность существенно сократить записи.
Письменность шумеров является столь же древней, как и письменность египтян. Принято считать, что шестидесятеричная
система была выбрана из метрологических соображений: число 60 имеет много делителей. Для записи чисел больше 59
древние вавилоняне впервые использовали новый принцип – одно из самых выдающихся достижений в развитии систем
обозначений чисел – принцип позиционности, т.е. зависимости значения символа от его местоположения в записи числа.
Римские обозначения чисел известны ныне лучше, чем любая другая древняя система счисления. Эта система возникла как
результат оперирования с палочками, выкладываемыми для счета на стол или доску. Обозначения чисел с помощью
палочек тесно связано со счетом на пальцах и счетной доске, но применялось оно также и в письменных вычислениях.
Первым европейский ученый, которой ввел в употребление в Европе арабские цифры, был Герберт, работавший в Испании
и позднее (в 999 г.) ставший папой Сильвестром II. В 12 в. Хуан из Севильи перевел на латынь трактат «Об индийских
числах» арабского математика Аль-Хорезми. Когда в следующем веке индийские обозначения стали широко известными,
новая система получила название алгоритм. Через пару столетий европейские алгоритмики одержали верх над теми, кто
пользовался римскими цифрами в вычислениях с целыми числами, но лишь с 1585 г. индо-арабская система обозначений,
систематически расширяясь, стала использоваться и применительно к дробям.
8.
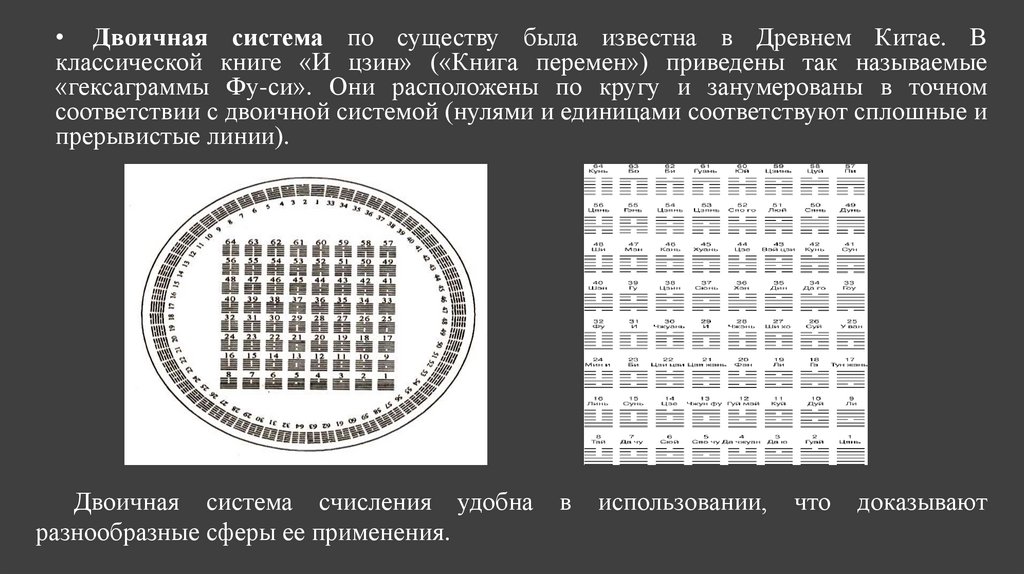
• Двоичная система по существу была известна в Древнем Китае. Вклассической книге «И цзин» («Книга перемен») приведены так называемые
«гексаграммы Фу-си». Они расположены по кругу и занумерованы в точном
соответствии с двоичной системой (нулями и единицами соответствуют сплошные и
прерывистые линии).
Двоичная система счисления удобна
разнообразные сферы ее применения.
в
использовании,
что
доказывают
9. Применение систем счисления
Азбука МорзеШтрих-коды
Компьютерная техника и
информационные технологии
10. Заключение
• В данной работе:1) рассмотрено понятие систем счисления, выделили их виды;
2) рассмотрена история возникновения и развитие систем счисления;
3) выделено применение различных систем счисления в жизни человека.
• Изучив литературу по теме «Системы счисления», я узнала, что в древности
люди пользовались различными системами счисления, позиционными и
непозиционными.
• Многие системы счисления имеют анатомическое происхождение. Элементы
некоторых систем счисления имеют практическое применение в наши дни.
• Общеупотребительной системой счисления стала десятичная система
счисления. Но и другие системы счисления имеют практическое применение,
например, системы счисления с основаниями 2, 8, 16.
• Правила, связанные с системами счисления помогают в практической
деятельности человека.
11. Литература
1. Аванта +. Энциклопедия для детей. Т. 22. Информатика. – М.: Аванта+,2004.
2. Аванта +. Энциклопедия для детей. Т. 11. Математика. – М.: Аванта+, 2004.
3. Занимательные материалы по математике. 7 – 8 классы. / Составитель
Галаева Е.А. – Волгоград: Издательско-торговый дом «Корифей», 2006. – 80
с.
4. Системы счисления и их применение. (Серия: «Библиотека
«Математическое просвещение»») / Гашков С.Б. – Москва: Издательство
Московского центра непрерывного математического образования, 2004. –
52 с., ил.
5. В.С. Кессельман. Занимательная математика. М.: АСТ: Астрель, 2008.











 Информатика
Информатика








