Похожие презентации:
Геометрическое место точек (ГМТ) пространства
1.
10 "А" КЛАСС ФМШ №56 Г. УЛАН-УДЭВасильев Дмитрий
Федотов Михаил
2.
Геометрически местомточек (ГМТ) пространства
называют множество точек
пространства, обладающих
одним определённым
свойством.
Например, окружность можно
определить как геометрическое место
точек, равноудалённых от данной
точки.
3.
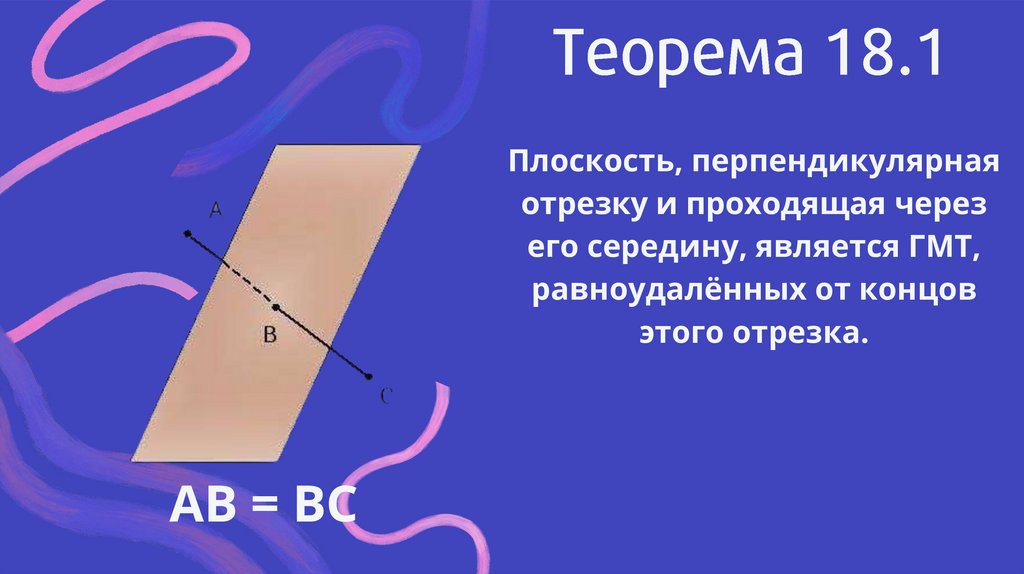
Плоскость, перпендикулярнаяотрезку и проходящая через
его середину, является ГМТ,
равноудалённых от концов
этого отрезка.
AB = BC
4.
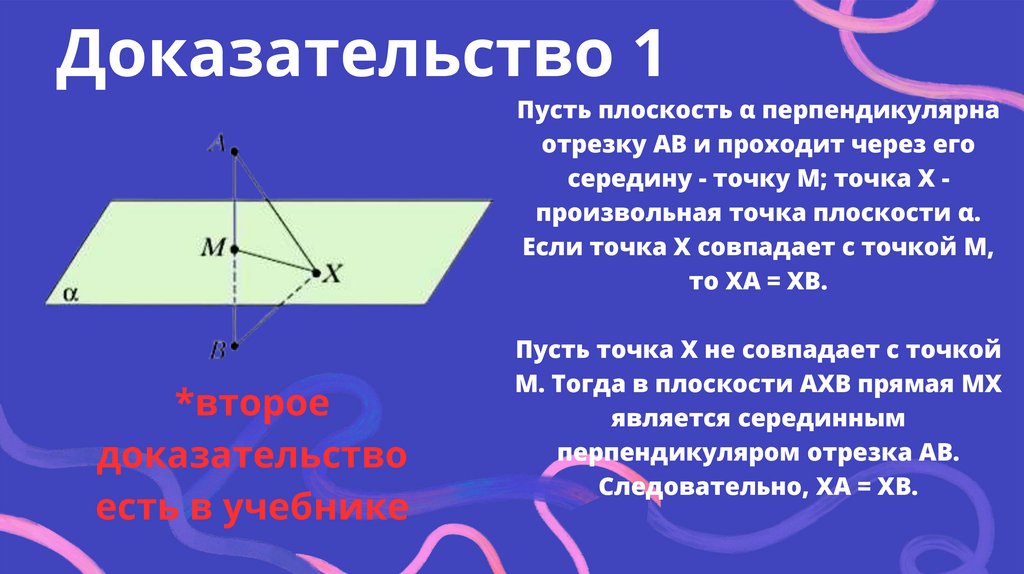
Доказательство 1Пусть плоскость α перпендикулярна
отрезку АВ и проходит через его
середину - точку М; точка Х произвольная точка плоскости α.
Если точка Х совпадает с точкой М,
то ХА = ХВ.
*второе
доказательство
есть в учебнике
Пусть точка Х не совпадает с точкой
М. Тогда в плоскости АХВ прямая МХ
является серединным
перпендикуляром отрезка AВ.
Следовательно, ХА = XВ.
5.
Биссектор двугранного угла?Полуплоскость, границей
которой является ребро
двугранного угла, делящая его
на два двугранных угла равной
величины, называется
биссектором двугранного угла.
6.
Теорема 18.2Биссектор двугранного угла
является ГМТ,
принадлежащих
двугранному углу и
равноудалённых от его
граней.
γ
α
β





 Математика
Математика








