Похожие презентации:
Некоторые свойства окружности. Касательная к окружности
1.
Некоторые свойстваокружности.
Касательная к
окружности
2.
ПовторениеC
Окружность (O;R)
AB – диаметр
А
O
B
ОС = ОА = ОВ – радиусы
АС - хорда
3.
Теорема 20.1Диаметр окружности, перпендикулярный
хорде, делит эту хорду пополам.
C
Дано: Окр.(O; R)
АВ – хорда
CD – диаметр
CD ⊥ АВ
Доказать: CD делит АВ пополам.
А
В
O
Доказательство:
1 случай
Если хорда АВ – диаметр, то CD пересекает
АВ в точке О, значит, АО = ВО.
D
4.
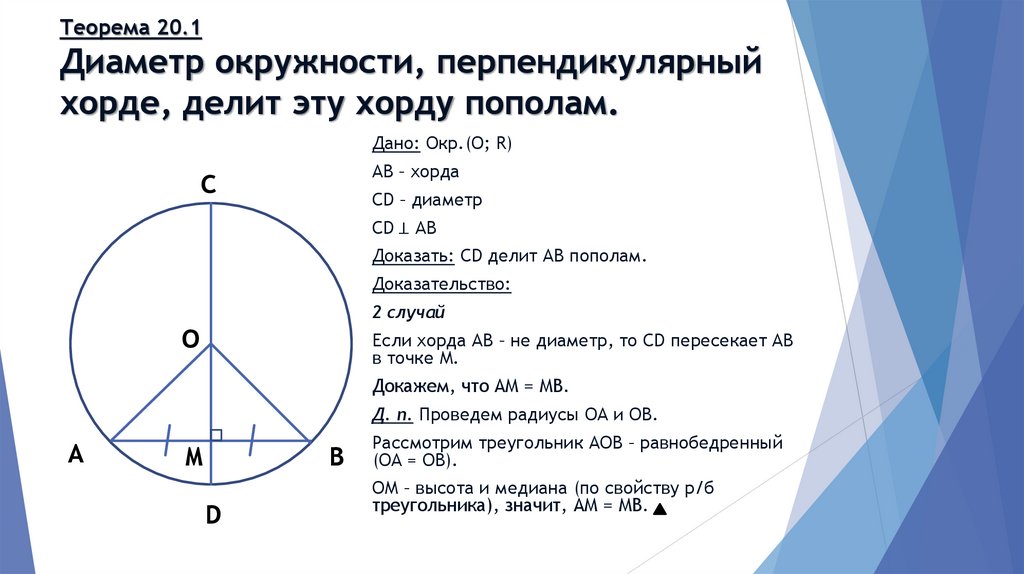
Теорема 20.1Диаметр окружности, перпендикулярный
хорде, делит эту хорду пополам.
Дано: Окр.(O; R)
АВ – хорда
C
CD – диаметр
CD ⊥ АВ
Доказать: CD делит АВ пополам.
Доказательство:
2 случай
O
Если хорда АВ – не диаметр, то CD пересекает АВ
в точке М.
Докажем, что АМ = МВ.
Д. п. Проведем радиусы ОА и ОВ.
А
М
В
D
Рассмотрим треугольник АОВ – равнобедренный
(ОА = ОВ).
ОМ – высота и медиана (по свойству р/б
треугольника), значит, АМ = МВ.
5.
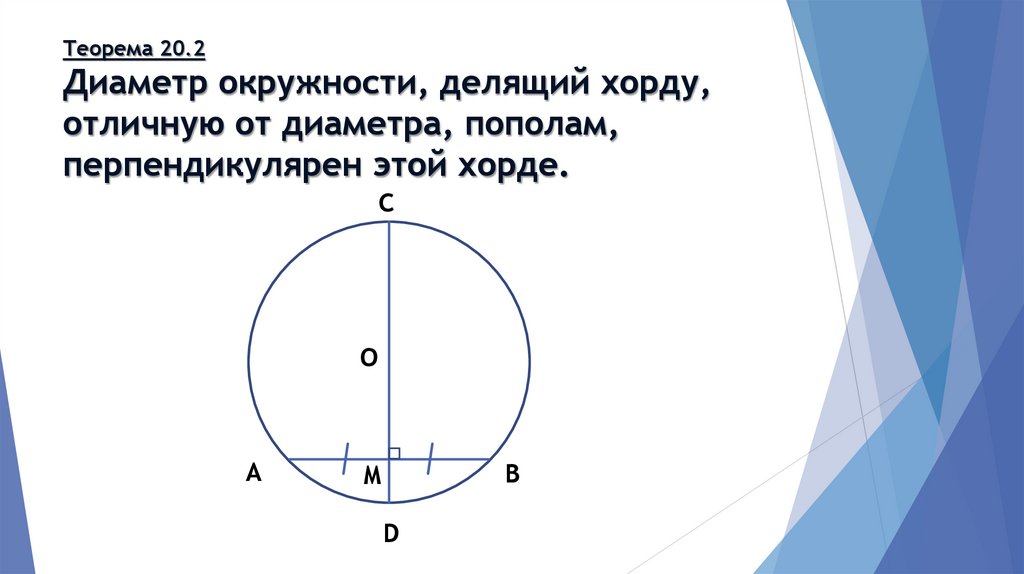
Теорема 20.2Диаметр окружности, делящий хорду,
отличную от диаметра, пополам,
перпендикулярен этой хорде.
C
O
А
В
М
D
6.
Рассмотрим взаимное расположениепрямой и окружности.
Вспомним, что называется расстоянием от точки до прямой?
Расстояние от точки до прямой – это длина перпендикуляра, опущенного из
этой точки к этой прямой.
СН ⊥ а
C
а
H
7.
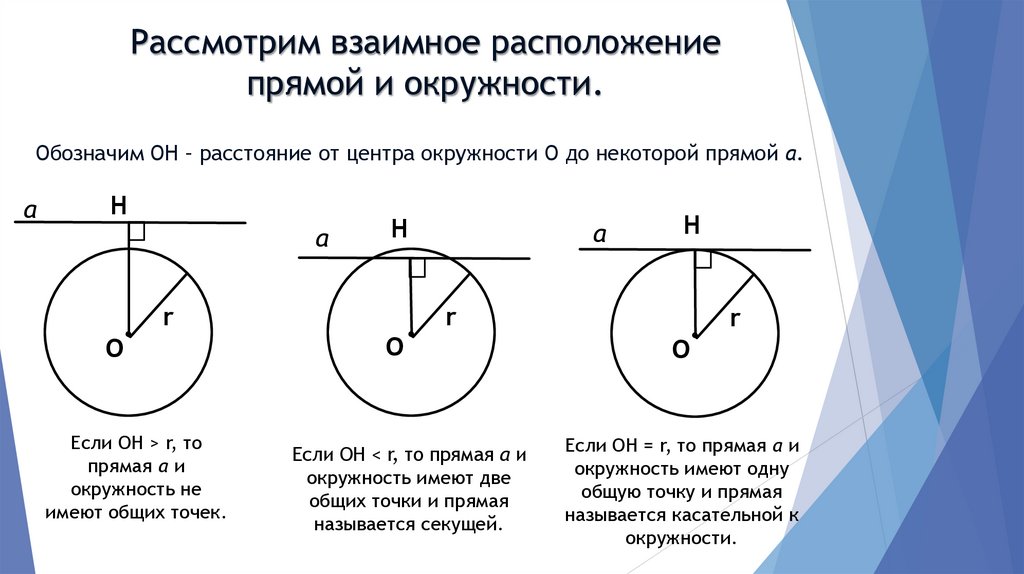
Рассмотрим взаимное расположениепрямой и окружности.
Обозначим ОН – расстояние от центра окружности О до некоторой прямой а.
а
Н
а
Н
r
O
Если ОН > r, то
прямая а и
окружность не
имеют общих точек.
а
Н
r
O
Если ОН < r, то прямая а и
окружность имеют две
общих точки и прямая
называется секущей.
r
O
Если ОН = r, то прямая а и
окружность имеют одну
общую точку и прямая
называется касательной к
окружности.
8.
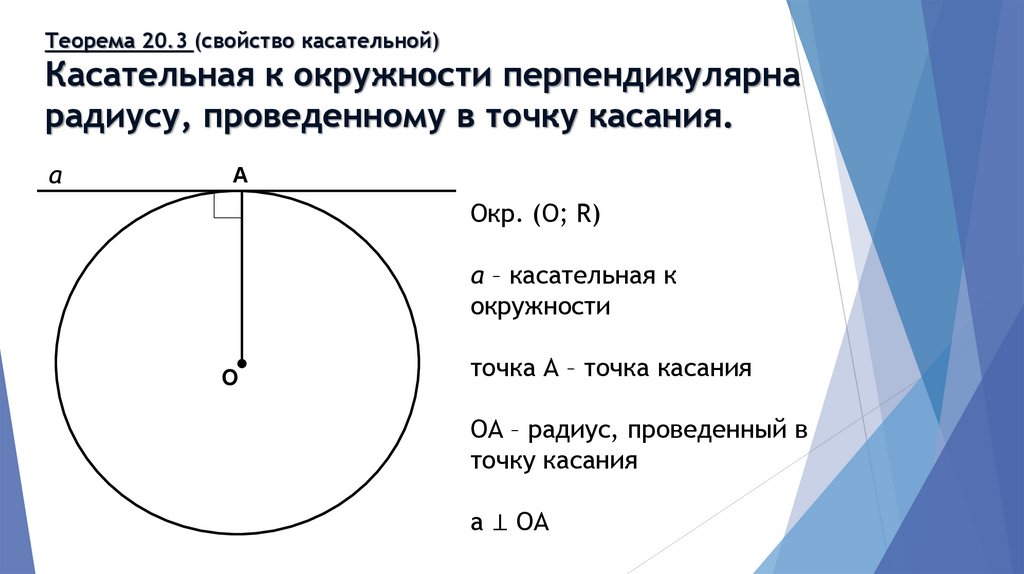
Теорема 20.3 (свойство касательной)Касательная к окружности перпендикулярна
радиусу, проведенному в точку касания.
а
А
Окр. (О; R)
а – касательная к
окружности
O
точка А – точка касания
ОА – радиус, проведенный в
точку касания
а ⊥ ОА
9.
Теорема 20.4 (признак касательной к окружности)Если прямая, проходящая через точку
окружности, перпендикулярна радиусу,
проведенному в эту точку, то эта прямая
является касательной к данной окружности.
Следствие
Если расстояние от центра окружности до
некоторой прямой равно радиусу
окружности, то эта прямая является
касательной к данной окружности.
10.
Задача. Докажите, что если через данную точку к окружностипроведены две касательные, то отрезки касательных,
соединяющих данную точку с точками касания, равны.
Дано: Окр.(O; R)
АВ, АС – касательные
Доказать: АВ = АС.
О
В
Доказательство:
С
Д.п. Радиусы ОВ и ОС.
По свойству касательной ОВ ⊥ АВ, ОС ⊥ АС.
А
Рассмотрим прямоугольные треугольники АОВ и АОС:
ОВ = ОС (как радиусы одной окружности)
АО – общая
Следовательно, Δ АОВ = Δ АОС (по катету и гипотенузе).
Значит, АВ = АС.
11.
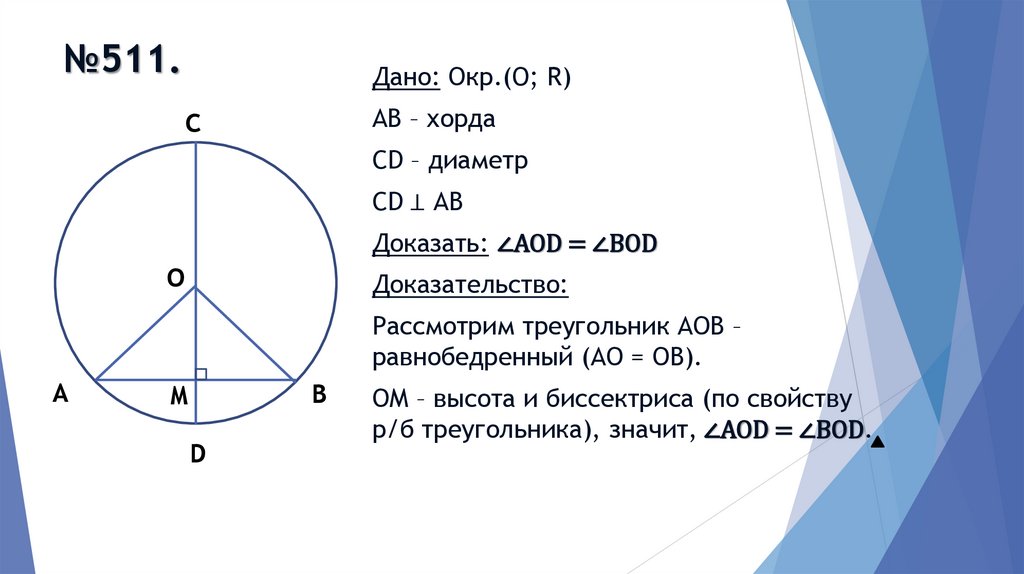
№511.Дано: Окр.(O; R)
АВ – хорда
C
CD – диаметр
CD ⊥ АВ
Доказать: ∠AOD = ∠BOD
O
Доказательство:
Рассмотрим треугольник АОВ –
равнобедренный (АО = ОВ).
А
В
М
D
ОМ – высота и биссектриса (по свойству
р/б треугольника), значит, ∠AOD = ∠BOD.
12.
Дано: Окр.(O; R)№512.
АВ = CD – хорды
OP и OM – расстояния от центра окружности до хорд
C
Доказать: OP = OM.
Доказательство:
Р
1) Рассмотрим Δ АОВ – р/б (ОА = ОВ).
ОМ – высота и медиана (по свойству р/б треугольника),
O
значит, АМ = МВ =
D
1
АВ.
2
2) Аналогично, Δ CОD – р/б (ОC = ОD) и CP = PD =
А
3) Т.к. AB = CD, то
М
В
1
CD.
2
1
1
AB = CD, значит, PD = AM.
2
2
4) Рассмотрим Δ OPD и Δ OMA - прямоугольные:
PD = AM (из доказанного), OD = OA (как радиусы), значит,
Δ OPD = Δ OMA (по катету и гипотенузе).
Отсюда, OP = OM.







 Математика
Математика








