Теория информации. Практическая работа 1. Оценка количества информации

1. Теория информации

Практическая работа 1
Оценка количества информации
Доцент каф. ЕНД и ИТ Шарапова ЛВ

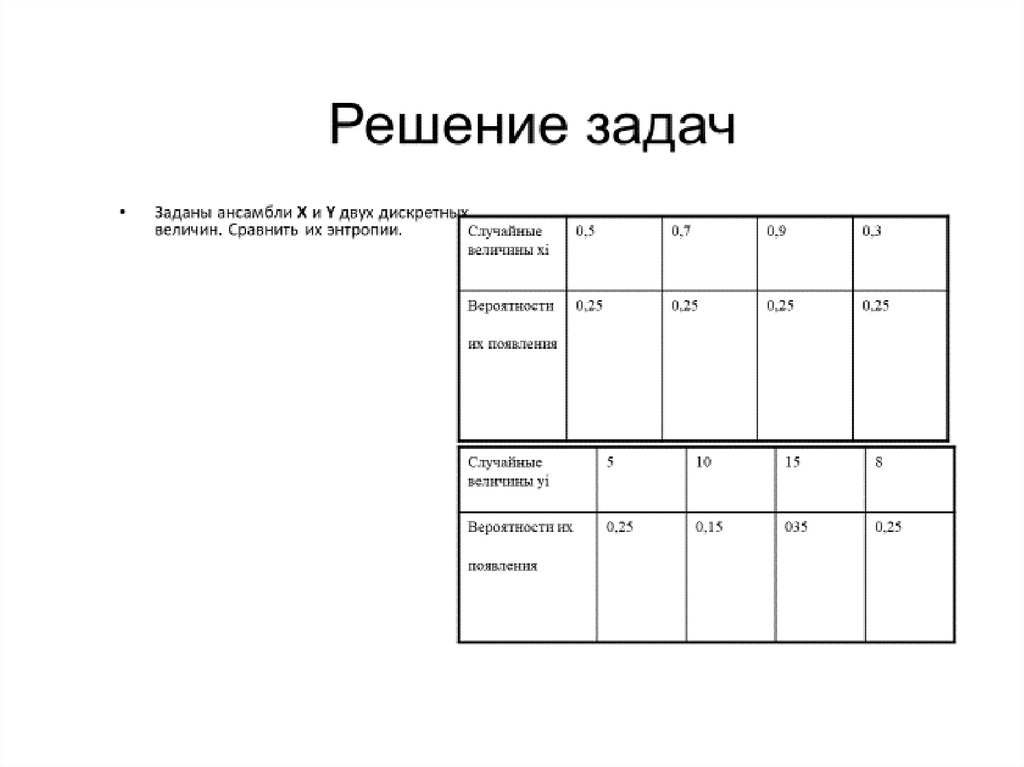
2. Решение задач

• Пользователь компьютера, хорошо
владеющий навыками ввода информации с
клавиатуры может вводить в минуту 100
знаков. Мощность алфавита, используемого
в компьютере равна 256. Какое количество
информации в байтах может ввести
пользователь за 1 минуту.

3. Решение задач

• При угадывании целого числа в некотором
диапазоне было получено 6 бит
информации. Сколько чисел содержит этот
диапазон?

4. Решение задач

• Какое количество информации несет
сообщение: «Встреча назначена на
сентябрь»?

5. Решение задач

• При угадывании целого числа в диапазоне
от 1 до N было получено 7 бит
информации. Чему равно N?

6. Решение задач

• В доме 14 окон. Сколько различных
сигналов можно подать, зажигая свет в
окнах? Сколько бит информации несет в
себе каждый такой сигнал?

7. Решение задач

• Определить количество информации,
которое содержится в телевизионном
сигнале, соответствующем одному кадру
развертки. Пусть в кадре 625 строк, а
сигнал, соответствующий одной строке,
представляет собой последовательность из
600 случайных по амплитуде импульсов,
причем амплитуда импульса может принять
любое из 8 значений с шагом в 1 В.

8. Решение задач

Оцените с точностью до одного
бита энтропию системы, которая может с
равной вероятностью находится
в 50 состояниях.

9. Решение задач

Может ли энтропия системы, которая
принимает случайным
образом одно из 4-х состояний, равняться:
а) 3; б) 2.1 в) 1.9 г) 1; д) 0.3?
Ответ объяснить.

10. Решение задач

Заданы три случайных величины X, Y, Z,
каждая из которых принимает по два
значения с вероятностями:
1. P(X = x1) = 0.6; P(X = x2) = 0.4;
2. P(Y = y1) = 0.1; P(Y = y2) = 0.9;
3. P(Z = z1) = 0.2; P(Z = z2) = 0.8 .
Запись P(X = x1) = 0.5 означает, что
случайная величина X принимает значение
x1 с вероятностью 0.5. Требуется
расположить энтропии этих систем в
порядке возрастания

11. Решение задач

Получены три различных сообщения A, B, C:
A= «прибытие в десять часов»;
B= «прибытие в десять часов ноль минут»;
C= «прибытие ровно в десять часов».
Используя энтропийный подход Шеннона,
сравните количество информации,
содержащееся в этих сообщениях.

12. Решение задач

Получены три различных сообщения A, B, C:
A= «прибытие в десять часов»;
B= «прибытие в десять часов ноль минут»;
C= «прибытие ровно в десять часов».
Используя энтропийный подход Шеннона,
сравните количество информации,
содержащееся в этих сообщениях.

13.

14. Решение задач

Алфавит состоит из букв a, b, c, d.
Вероятности появления букв равны
соответственно 0,25; 0,25; 0,34; 0,16.
Определить количество информации,
приходящееся на символ сообщения,
составленного с помощью такого алфавита.

15. Решение задач

Х
х1
х2
х3
х4
х5
х6
х7
х8
р
0,1
0,12
0,1
0,1
0,1
0,09
0,07
0,32
Определить число N значений случайной величины, при которых
энтропия равномерного распределения равна энтропии заданного
распределения.

16. Решение задач

• В алфавите племени БУМ всего 4 буквы (А,
У, М, Б), один знак препинания (.) и для
разделения слов используется пробел.
Подсчитали, что в популярном романе
«МУБА» содержится 10000 знаков, из них:
букв А – 4000, букв У – 1000, букв М – 2000,
букв Б – 1500, точек – 500, пробелов – 1000.
Найти энтропию книги.