Занимательные задачи в курсе начала математического анализа

1.

ЗАНИМАТЕЛЬНЫЕ ЗАДАЧИ В
КУРСЕ НАЧАЛА
МАТЕМАТИЧЕСКОГО АНАЛИЗА
Работу выполнила студентка МФ-111
Кремнева Дарья

2.

Цель работы:Ознакомление с софизмами и
парадоксами на основе собственных исследований
Задачи работы:
1.Дать определение понятиям «Софизм»и «Парадокс»
2.Привести примеры этих занимательных задач и вариантов их
решения
3.Определить практическую значимость заданий с софизмами и
парадоксами в учебной деятельности

3.

Актуальность работы
Разбор данных задач прежде всего развивает
логическое мышление.
Тема софизмов сейчас актуальна , т.к софизм - это
обман , а он окружает нас в современном мире.
Найти ошибку в софизме-значит не дать себя
обмануть

4.

Софизмформально кажущееся
правильным, но по
существу ложное
умозаключение,
основанное на
преднамеренно
неправильном подборе
исходных положений
Парадокс-высказывание, мнение, рассуждение, которое расходится с
общепринятым мнением и кажется нелогичным или противоречащим
здравому смыслу (зачастую лишь при поверхностном понимании).

5.

Софизм Ахиллеса и черепахи
Пусть черепаха начинает гонку, находясь в 1000 шагах впереди
Ахиллеса. Также предположим, что Ахиллес бежит в 10 раз быстрее
черепахи. осле старта за то время, которое Ахиллес пробежит эти
1000 шагов, черепаха успеет проползти 100 шагов. Когда Ахиллес
пробежит эти 100 шагов, черепаха проползет еще 10 шагов и
тд.Догонит ли Ахиллес черепаху?

6.

Парадокс суммы
Сумма всех натуральных чисел равна
ОТРИЦАТЕЛЬНОЙ ДРОБИ! Как это возможно?
S-S1+
=4S
S-4S=

7.

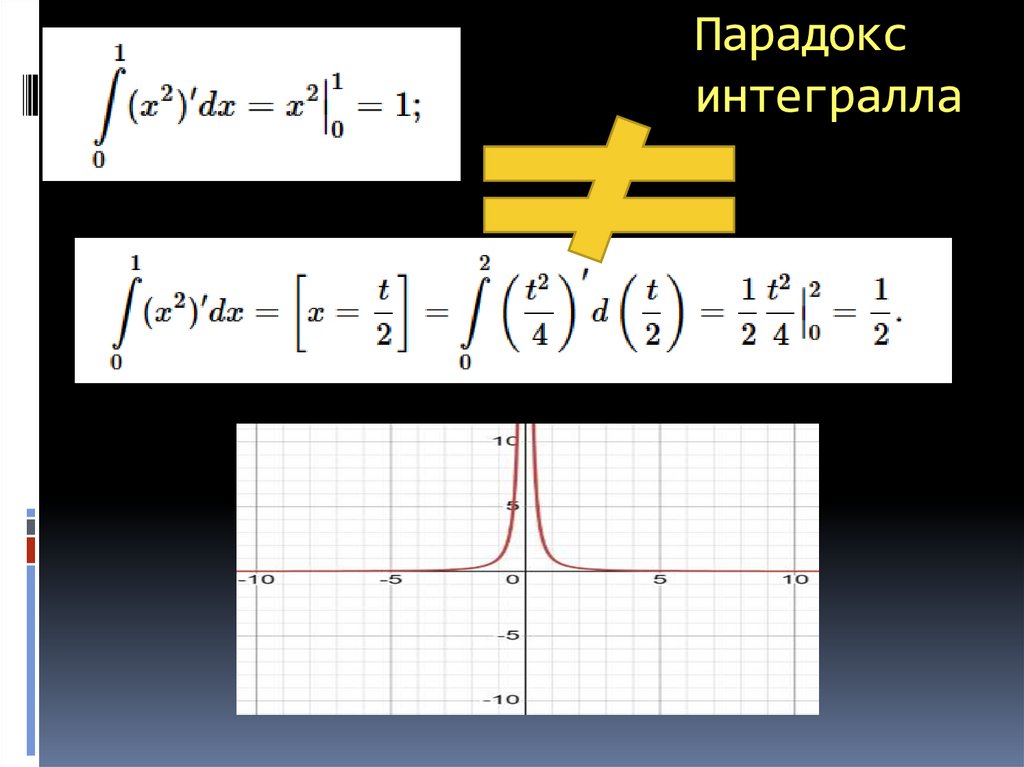
Парадокс
интегралла

8.

Парадокс Дня Рождения
Парадо́кс дней рожде́ния — утверждение,
состоящее в том, что в группе, состоящей из 23
или более человек, вероятность
совпадения дней рождения (число и месяц)
хотя бы у двух людей превышает 50 %.
Например, если в классе 23 ученика или более,
то более вероятно то, что у какой-то пары
одноклассников дни рождения придутся на
один день, чем то, что у каждого будет свой
неповторимый день рождения. Для 57 и более
человек вероятность такого совпадения
превышает 99 %, хотя 100 % она достигает,
согласно принципу Дирихле (здравому смыслу),
только тогда, когда в группе не менее 367
человек

9.

Парадокс стрелы
Парадокс заключается в следующем: Чтобы
преодолеть путь, нужно сначала преодолеть
половину пути, а чтобы преодолеть половину
пути, нужно сначала преодолеть половину
половины, и так до бесконечности.

10.

Парадокс раздела ставки
Два игрока играют в честную игру (т.е. у обоих
шансы победить одинаковы), и они
договорились, что тот, кто первым выиграет 6
партий, получит весь приз. Предположим, что на
самом деле игра остановилась до того, как один
из них выиграл приз (например, первый игрок
выиграл 5 партий, а второй – 3). Как
справедливо следует разделить приз?

11.

Практическая значимость в учебной
деятельности
Собранный мной материал
можно использовать на
факультативных занятиях, на
занятиях математического
кружка. Учителя математики
могут использовать его на
уроках, чтобы привить
интерес учащихся к предмету.
Также рекомендую
ознакомиться со своей
работой тем сверстникам,
которые хотят знать о
математике больше, чем
рядовой школьник.