389.59K

Категория:

Лингвистика

Похожие презентации:

Научно-технический перевод. Различия перевода научно-технических текстов в английском и русском языках

Современная морфология: основные понятия, проблемы и подходы

Теория языка. Норман Борис Юстинович

Комплексная диагностика дизорфографий

Психолингвистика

Язык, общество, культура

Namangan Muhandislik Qurilish Instituti

1.

O’zbekiston Respublikasi Oliy va o’rta maxsus ta’lim vazirligi
Namangan Muhandislik Qurilish Instituti
“Bino va inshootlar qurilishi” kafedrasi dotsenti, t.f.n.
Xodjiev N.R.
«Inshootlar dinamikasi va ustvorligi» fanidan
№ 1 Ma’ruza
Kirish. Inshootlar dinamikasining maqsad va
vazifalari.
Namangan -2023

2.

Reja
1. Inshootlar dinamikasining
maqsad va vazifalari.
2. Dinamik kuchlar turlari.
3. Sistemaning erkinlik darajasi.

3.

Динамика и устойчивости
сооружений
План
1. Цели и задачи динамики
сооружений.
2. Типы динамических сил.
3. Степень свободы системы.

4.

Dynamics and stability of
structures
Plan
1. Goals and objectives of the
dynamics of structures.
2. Types of dynamic forces.
3. The degree of freedom of the
system.

5.

INSHOOTLAR
DINAMIKASI VA
USTVORLIGI
Kirish.
Inshootlar dinamikasining maqsad va
vazifalari.

6.

TAVSIYA ETILGAN O'QUV-METODIK ADABIYOTLAR
(Strukturaviy dinamika va barqarorlik)
O'quv qo'llanmalar
1. Александров А.В., Потапов В.Д.,Зылев В.Б. Строительная механика. В 2 кн. Кн.2.
Динамика и устойчивость упругих систем : учеб. для вузов / под ред. А.В. Александрова. –
М. : Высш. шк., 2008. – 384 с
2. Леонтьев Н.Н., Соболев Д.Н., Амосов А.А. Основы строительной механики
стержневых систем : учеб. для строит. спец-тей. вузов. – М. : Изд-во АСВ, 1996. – 541 с.
3. Шапошников Н.Н. Строительная механика: учебник. – 13-е изд., перераб. и доп. – СПб. :
Изд-во «Лань», 2012. – 704 с. (Предыдущие : Дарков А.В., Шапошников Н.Н. Строительная
механика. – 12-е изд., стер., 2010 . – 656 с., 12-е изд., стер., 2008. – 656 с.)
4. Киселёв В.А. Строительная механика: Спец. курс. Динамика и устойчивость сооружений. –
М. : Стройиздат, 1980. – 616 с.
O'quv-uslubiy adabiyotlar
1. Себешев В.Г. Строительная механика. Часть III. Динамика и устойчивость сооружений
( иллюстративный конспект лекций ) : учеб. пособие [Электронный ресурс]. –
Новосибирск : НГАСУ (Сибстрин), 2009. – 180 сл.
2. Себешев В.Г. Динамика деформируемых систем с конечным числом степеней свободы масс :
учеб. пособие. – Новосибирск : НГАСУ (Сибстрин), 2011. – 227 с.
3. Себешев В.Г. Расчёт стержневых систем на устойчивость методом перемещений :
учебное пособие [Электронный ресурс]. – 2-е изд., стер. – Новосибирск: НГАСУ (Сибстрин),
2013. – 84 с.
4. Крамаренко А.А., Широких Л.А. Устойчивость и динамика сооружений : сборник задач
для самостоятельной работы студентов. – Новосибирск: НГАС, 1994. – 36 с.
5. Безухов Н.И. Устойчивость и динамика в примерах и задачах :
учеб. пособие для строит. спец-тей. вузов. – М. : Высшая школа, 1987. – 264 с.
6. Роев В.И. Устойчивость упругих стержневых систем. Метод перемещений : Метод. указания
для студентов спец-ти. 2903 «Пром. и гражд. строит-во». – Новосибирск : НГАС, 1997. – 41 с.

7.

KONTSEPTSIYALAR
VA ATAMALAR
STRUKTURAVIY
DINAMIKA

8.

Tuzilmalar dinamikasimavzoʻʼhoi mazkur
printsiplari va usullari
Shiddat bilan tadqiqotdeformatsiyalangan holat
tuzilmalar (tuzilmalar)
dinamik ta'sirlar ostida.
предметом которого являются
принципы и методы
исследования напряжённодеформированного состояния
сооружений (конструкций)
при динамических воздействиях.

9.

Dinamik effektlar jismoniy tabiatda har xil
tashqi majburlovchi ta'sirlar
(kuch, kinematik va boshqalar),
qiymatga ega bo'lgan vaqt o'zgarishi,
murojaatning yo'nalishi va/yoki joyi,
deformatsiyalanuvchining harakatiga sabab bo'lmoqda
mexanik tizim va hisobot
uning tezlanish massalari, uning ta'siri
tangʻa-deformatsiyalangan
holatni e'tiborsiz qolab bo'lmaydi
(hisoblashning kerakli to'g'riligi bilan)
boshqalarning ta'siri bilan solishtirganda
bu tizimga taʼsir koʻrsatadi,
vaqt o'tishi bilan o'zgarmas.
Динамические воздействия -
это различные по физической природе
внешние вынуждающие воздействия
(силовые, кинематические и пр.),
изменяющиеся во времени по значению,
направлению и/или месту приложения,
вызывающие движение деформируемой
механической системы и сообщающие
её массам ускорения, влиянием которых
на напряжённо-деформированное
состояние нельзя пренебрегать
(при требуемой точности расчета)
в сравнении с влиянием других
воздействий на данную систему,
неизменных во времени.

10.

Dinamik ta'sirlar
klassifikatsiyasi
- Kelib chiqishi bo'yicha
Tabiiy
texnogen
– jismoniy tabiat bo'yicha
kuchlanish (yuklamalar)
kinematik (bog'lanish
taraflamalari)
harorat (?)
boshqalar (elektromagnit va boshqalar)
– maqomi bo'yicha
Ta'sir ko'rsatish sohalari
qurilish maydonida
– muddati bo'yicha
Taʼsiri
– belgisi bo'yicha
vaqtdagi o'zgarishlar
Mobil
Hali
Uzun
Qisqa
Dürtüsel
Birdan
murakkab qonun asosida Jadval
Garmonik

11.

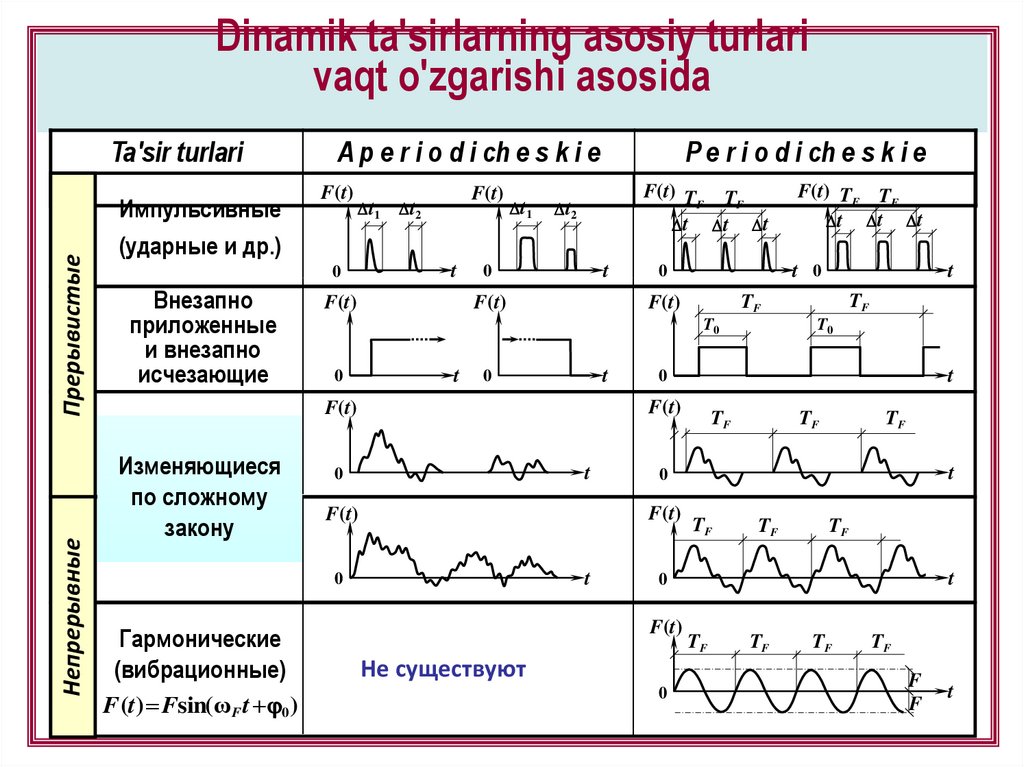
Dinamik ta'sirlarning asosiy turlari
vaqt o'zgarishi asosida
Непрерывные
Прерывистые
Ta'sir turlari
Импульсивные
(ударные и др.)
A p e r i o d i ch e s k i e
F(t)
D t1
0
Внезапно
приложенные
и внезапно
исчезающие
F(t)
D t2
t
F(t)
D t1
F(t) T
D t2
F
Dt
t
0
F(t)
0
t
t
0
t
t
F (t ) Fsin(ωF t 0 )
TF
T0
t
0
TF
TF
TF
t
0
F(t)
F(t)
t
TF
F(t)
0
F(t) TF TF
Dt Dt Dt
t 0
0
T0
0
Гармонические
(вибрационные)
TF
Dt Dt
F(t)
F(t)
Изменяющиеся
по сложному
закону
P e r i o d i ch e s k i e
TF
TF
TF
t
0
F(t)
Не существуют
0
TF
TF
TF
TF
F
F
t

12.

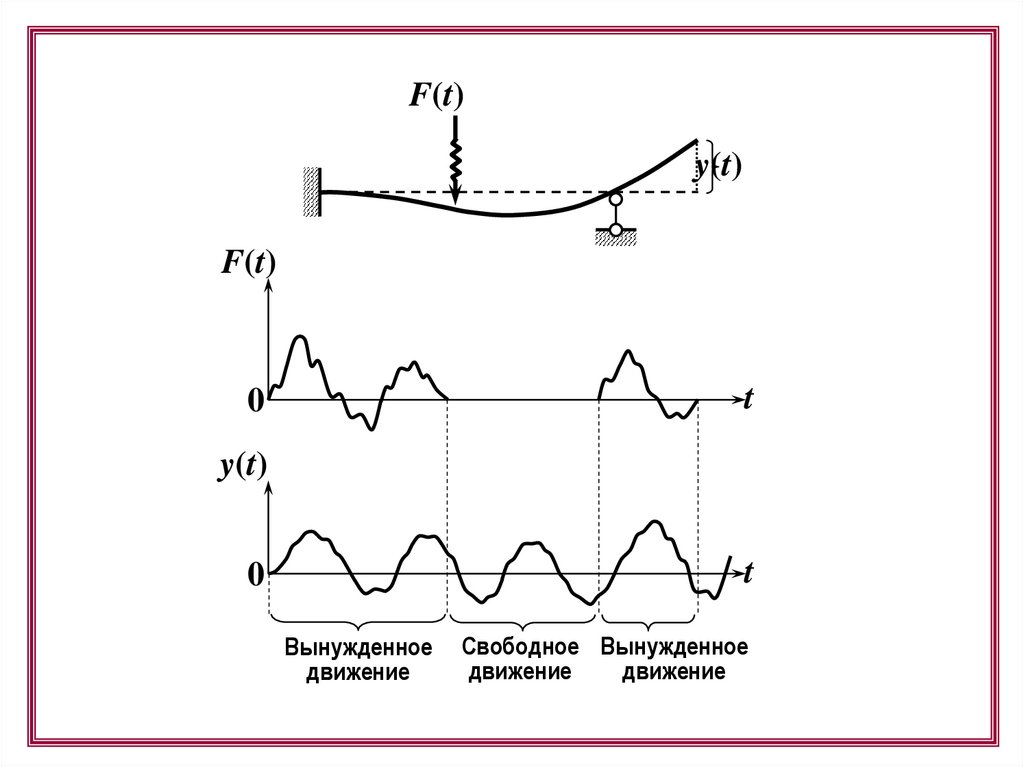
Вынужденное движение –
движение механической системы
в то время, когда к ней
приложены динамические воздействия.
Свободное движение –
движение системы, обусловленное
начальным запасом механической энергии
и происходящее
без вынуждающих динамических
воздействий
( в те промежутки времени, когда
динамические воздействия отсутствуют ).

13.

F(t)
y(t)
F(t)
t
0
y(t)
t
0
Вынужденное
движение
Свободное Вынужденное
движение
движение

14.

Свободное движение происходит
«по инерции».
Инерцией (инертностью)
называется свойство материального тела
(системы), проявляющееся в сохранении
движения, совершаемого им при отсутствии
вынуждающих воздействий, и в постепенном
изменении этого движения с течением времени
при возникновении динамических воздействий.
Мерой инерции является масса.
Следствие: свойство инерции присуще механическим,
в т.ч. деформируемым, системам, обладающим массами.

15.

Колебания
(механические) –
частный случай движения,
характеризующийся некоторой
повторяемостью во времени
параметров НДС системы.
y(t)
F(t)
y(t)
0
t

16.

Периодические колебания –
колебания, при которых значения
некоторого (любого) параметра Р(t)
НДС системы в точности повторяются
через один и тот же промежуток времени Т,
называемый периодом колебаний:
P(t) = P(t +kT ), где k – любое целое число.
y(t)
F(t)
Т
Т
Т
Т
y(t)
0
t

17.

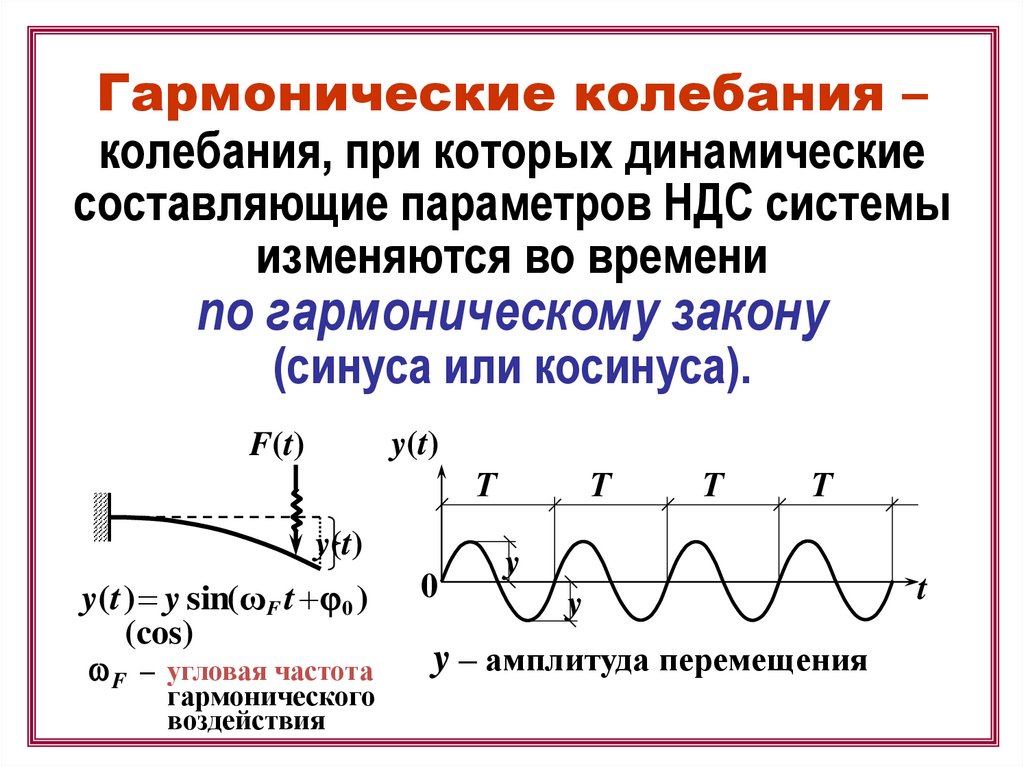
Гармонические колебания –
колебания, при которых динамические
составляющие параметров НДС системы
изменяются во времени
по гармоническому закону
(синуса или косинуса).
y(t)
F(t)
Т
Т
y(t)
y(t ) y sin(ωF t 0 )
(cos)
wF – угловая частота
гармонического
воздействия
0
Т
Т
y
y
y – амплитуда перемещения
t

18.

Собственные колебания –
частный случай свободного движения,
характеризующийся
синфазным моногармоническим
движением всех масс системы
(то есть гармоническим движением масс
с одной общей частотой w и в одной фазе (t)):
yi (t) = yi sin (t), i = 1, 2, ... , n; (t) = wt + 0 .
w – угловая частота собственных колебаний
k
yi(t)
yi
i
yk(t) yk
yi ( t ) yi
const
yk ( t ) yk
(стоячая волна)

19.

Главная форма колебаний –
определенный вид стоячих волн,
образуемых осевыми линиями
или срединными поверхностями
элементов системы
при собственных колебаниях
с некоторой частотой.

20.

Степени свободы масс –
независимые
геометрические параметры,
полностью определяющие
положение масс системы
в произвольный момент
движения.
Системы с распределёнными массами
n

21.

Степени свободы масс –
независимые
геометрические параметры,
полностью определяющие
положение масс системы
в произвольный момент
движения.
Системы с сосредоточенными массами: 1 n
Неточечная
масса
ds
h
ds
Точечные
массы
ds

22.

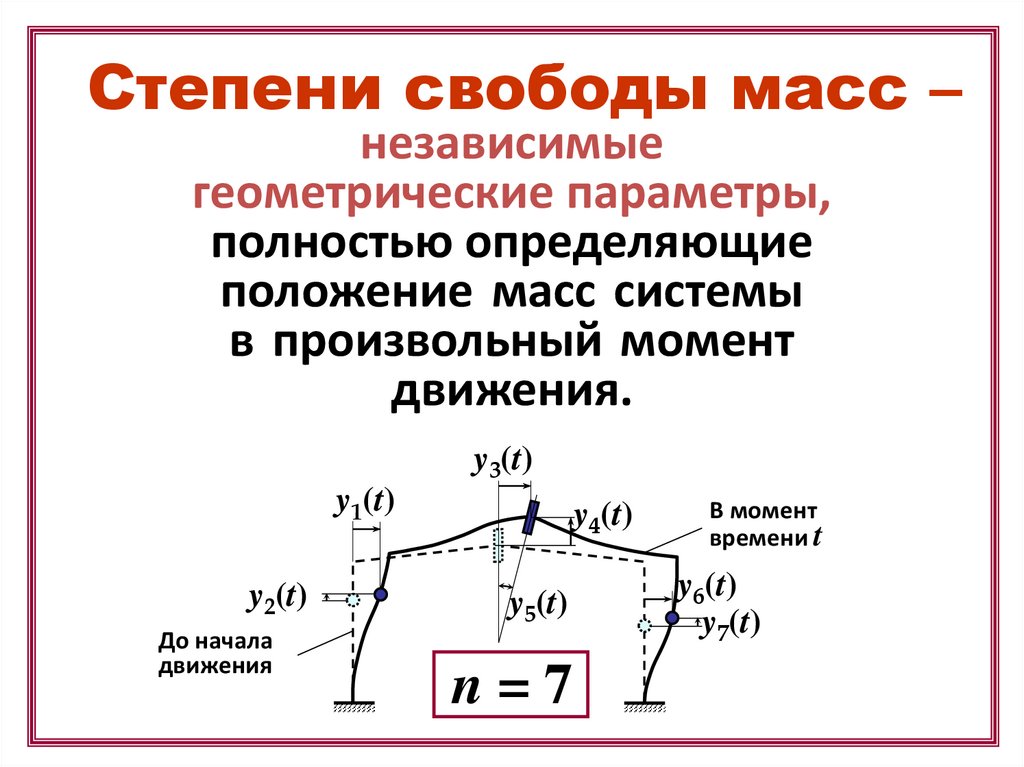
Степени свободы масс –
независимые
геометрические параметры,
полностью определяющие
положение масс системы
в произвольный момент
движения.
y3(t)
y1(t)
y2(t)
До начала
движения
y4(t)
y5(t)
n=7
В момент
времени t
y6(t)
y7(t)

23.

Степени свободы масс –
независимые
геометрические параметры,
полностью определяющие
положение масс системы
в произвольный момент
движения.
В случае применения
гипотезы l j :l j
До начала
движения
y2(t)
y1(t)
y3(t)
y4(t)
n=5
В момент
времени t
y5(t)

24.

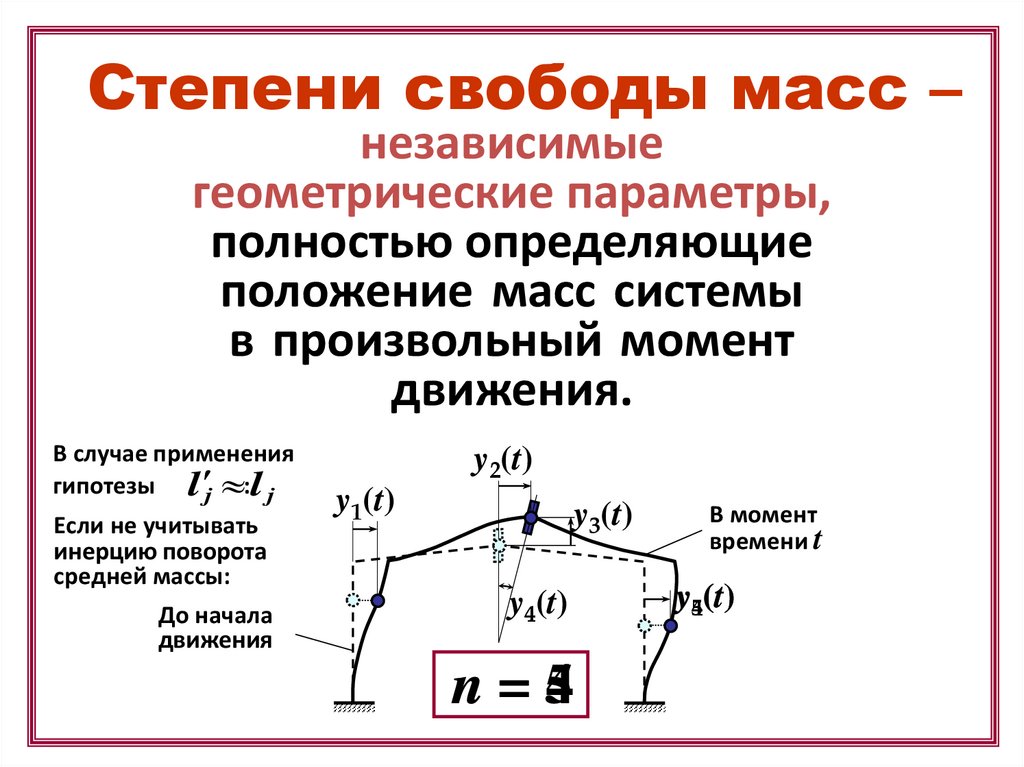
Степени свободы масс –
независимые
геометрические параметры,
полностью определяющие
положение масс системы
в произвольный момент
движения.
В случае применения
гипотезы l j :l j
Если не учитывать
инерцию поворота
средней массы:
До начала
движения
y2(t)
y1(t)
y3(t)
y4(t)
n = 54
В момент
времени t
y54(t)

25.

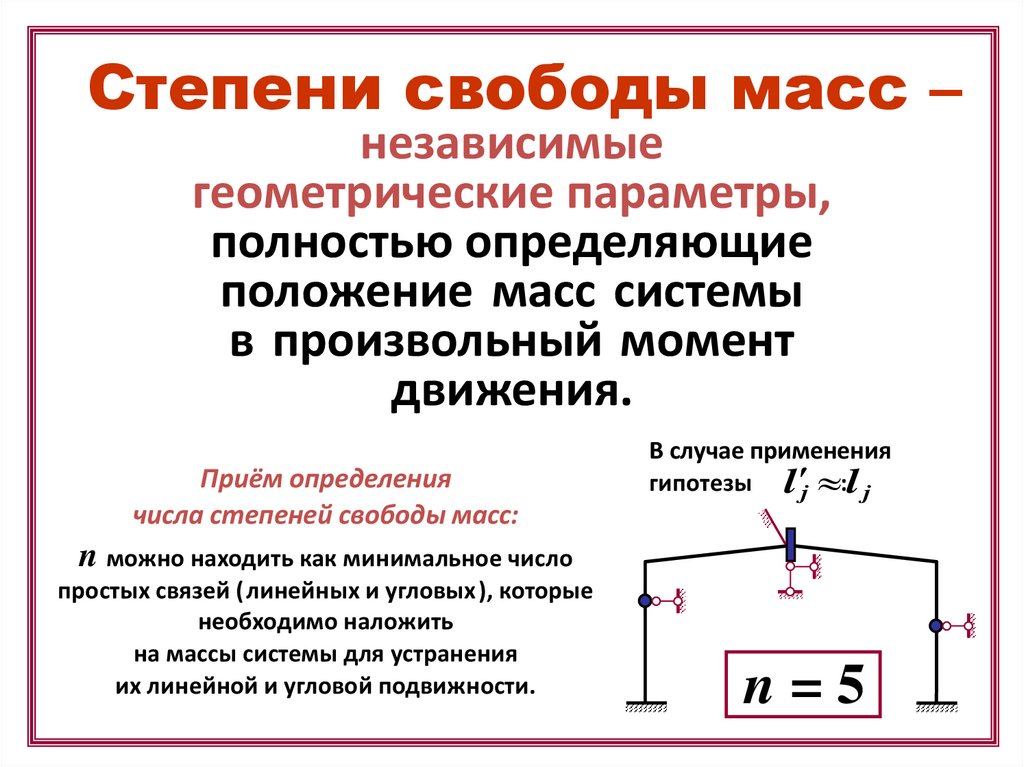
Степени свободы масс –
независимые
геометрические параметры,
полностью определяющие
положение масс системы
в произвольный момент
движения.
Приём определения
числа степеней свободы масс:
В случае применения
гипотезы l j :l j
n можно находить как минимальное число
простых связей ( линейных и угловых ), которые
необходимо наложить
на массы системы для устранения
их линейной и угловой подвижности.
n=5

26.

Основные задачи
расчёта сооружения (конструкции)
на динамические воздействия
1) определение частот и форм собственных колебаний
в целях
– недопущения возникновения явления резонанса;
– определения расчётных параметров сложных динамических
воздействий (сейсмических, аэродинамических и др.);
– расчёта демпфирующих устройств (сейсмозащиты,
гасителей колебаний и т.п.);
2) выявление законов изменения перемещений, скоростей
и ускорений точек сооружения, а по ним –
параметров НДС конструкций и их экстремальных значений
– для обеспечения динамической прочности (в том числе
выносливости), жёсткости и устойчивости сооружения в
целом и его частей;
– для предотвращения вредных ударных и вибрационных
воздействий на людей.

27.

Методы решения
задач динамики
– кинетостатический;
– энергетический.

28.

Кинетостатический метод –
метод, основанный на использовании
принципа Д’Аламбера ( J.B.L. D’Alembert, 1743 )
и заключающийся в замене
исходной динамической задачи
условной задачей на исследование
равновесия системы с дополнительно
приложенными к массам инерционными
силовыми факторами (силами инерции).
Закон инерции:
J ( t ) m y ( t )
d 2 y (t )
– y ( t )
dt 2
ускорение
( линейное, угловое )
П р и м е ч а н и е:
здесь и далее термин «закон инерции» используется условно, для краткости –
по смысловой аналогии с физическими законами ( Гука и др. ) –
не ассоциировать с 1-м законом Ньютона.

29.

Энергетический метод
основан на использовании
экстремальных свойств
полной механической энергии
движущейся системы.

30.

Контрольные вопросы
( в скобках даны номера слайдов, на которых можно найти ответы на вопросы;
для перехода к слайду с ответом можно сделать щелчок мышью по номеру в скобках*);
для возврата к контрольным вопросам сделать щелчок правой кнопкой мыши
и выбрать «Перейти к слайду 26» )
1. Что является предметом науки ( учебной дисциплины ), называемой
динамикой сооружений? ( 4 )
2. Какие воздействия на сооружения и конструкции называются динамическими? ( 5 )
3. Как классифицируются динамические воздействия по различным признакам? ( 6 )
4. Основные виды динамических воздействий по характеру изменения во времени. ( 7 )
5. Что такое инерция и что является мерой инерции? ( 10 )
6. Какие механические системы обладают свойством инерции? ( 10 )
7. Какое движение механической системы называется вынужденным, а какое
свободным? ( 8 )
8. Что такое механические колебания? ( 11 )
9. Какие колебания называются периодическими? ( 12 ) гармоническими? ( 13 )
10. Дайте определение собственных колебаний. ( 14 )
11. Что такое главная форма колебаний? ( 15 )
12. Что называется степенями свободы в динамике сооружений? ( 16 )
13. Каково число степеней свободы масс (ЧССМ) системы с распределёнными
массами? ( 16 )
14. Какими должны быть массы системы, чтобы число их степеней свободы было
конечным? ( 17 )
15. Как использование различных рабочих гипотез влияет на ЧССМ? ( 17 – 20 )
16. С помощью какого практического приёма можно определять ЧССМ? ( 21 )
*) Только в режиме «Показ слайдов»

31.

English Русский Правила