Похожие презентации:
Рекурсія
1.
ЛекціяРЕКУРСІЯ
Recursion
Лектор: к.т.н. Трофименко О.Г.
2.
3.
Обчислення факторіалаfactorial(n) :=n!
:= n * (n-1) * … * 2 * 1
4.
Ітеративна реалізаціяТипова ітеративна реалізація функції обчислення факторіалу на С++:
int factorial_iter (int n)
{
int i, f=1;
for(i=1; i <= n; i++) f *= i;
return f;
}
5.
Рекурсивне визначення6.
Рекурсивне визначенняРекурсивна реалізація обчислення факторіалу
int factorial_rec (int n)
{
if(n == 1) return 1;
return n * factorial_rec(n-1);
}
7.
Ітеративна версіяint factorial_iter (int n)
{
int i, f=1;
for(i=1; i <= n; i++) f *= i;
return f;
}
Виконання цієї програми генерує лінійний ітераційний процес:
8.
Рекурсивна версіяint factorial_rec(int n)
{
If (n == 1) return 1;
else return n * factorial_rec(n-1));
}
Це генерує лінійний рекурсивний процес:
fac_rec(5)
(5 * fac_rec(4))
(5 * (4 * fac_rec(3)))
(5 * (4 * (3 * fac_rec(2))))
(5 * (4 * (3 * (2 * fac_rec(1)))))
(5 * (4 * (3 * (2 * 1))))
(5 * (4 * (3 * 2)))
(5 * (4 * 6))
(5 * 24)
(120)
9.
• Приклад: обчислення для numb=3.fac(3) :
3 == 1 ?
No.
fac(3) = 3 * fac(2)
fac(2) :
2 == 1 ?
No.
fac(2) = 2 * fac(1)
fac(1) :
1 == 1 ?
Yes.
return 1
fac(2) = 2 * 1 = 2
return fac(2)
int fac(int numb){
if(numb==1)
fac(3) = 3 * 2 = 6
return 1;
return fac(3)
else
fac(3) має значення 6
return numb * fac(numb-1);
}
10.
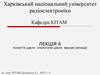
Обчислення 3!fact(1)
1
fact(3)
fact(2)
fact(3)
fact(2)
fact(3)
fact(2)
fact(3)
main()
main()
main()
main()
main()
main()
Крок 2:
Push: fact(3)
Крок 3:
Push: fact(2)
Крок 4:
Push: fact(1)
Крок 5:
Pop: fact(1)
повертає 1.
Крок 6:
Pop: fact(2)
повертає 2.
Крок 7:
Pop: fact(3)
повертає 6.
Всередині findFactorial(3):
if (number <= 1) return 1;
else return (3 * factorial (2));
Всередині findFactorial(2):
if (number <= 1) return 1;
else return (2 * factorial (1));
fact(3)
Всередині findFactorial(1):
if (number <= 1) return 1;
else return (1 * factorial (0));
2
6
11.
Що таке рекурсія?• Цикл без оператора циклу
• Функція, яка є частиною власного визначення
• Може працювати лише в тому випадку, якщо існує умова
завершення (базовий випадок), інакше вона працює
нескінчено
12.
Як здійснюється рекурсіяКожен раз, коли викликається функція,
значення функції, локальні змінні,
параметри та адреси зберігаються у стеку.
13.
Якщо ми використовуємо ітерацію, то повинні бути обережні, щобвипадково не створити нескінченний цикл :
for(int incr=1; incr!=10; incr+=2)
...
int result = 1;
while(result >0){
...
result++;
}
Oops!
Oops!
14.
Аналогічно, якщо ми використовуємо рекурсію, то повинні бути обережними, щобне створити нескінченний ланцюжок викликів функцій:
int fac(int numb){
return numb * fac(numb-1);
}
Oops!
No termination
condition
або:
int fac(int numb){
if (numb<=1)
return 1;
else
return numb * fac(numb+1);
}
Oops!
15.
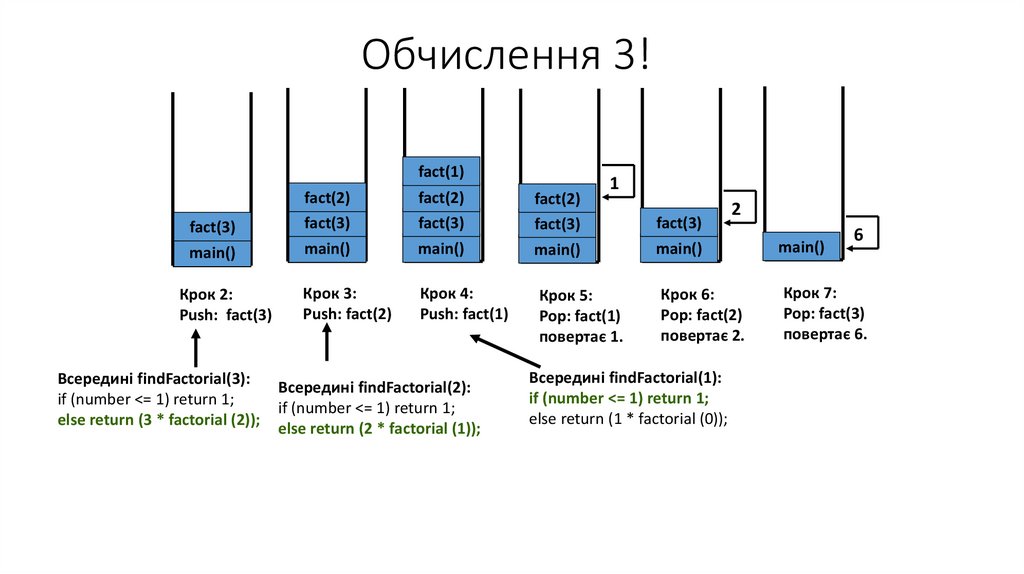
Типи рекурсіїАлгоритм рекурсії може бути
реалізовним більш ніж одним
способом. Можливі варіанти рекурсії
це лінійна, хвостова, обопільна,
двійкова і вкладена.
Ви можете здійснити їх або під час
компіляції через використання
шаблонів або під час виконання
через використання функцій або
функцій членів.
16.
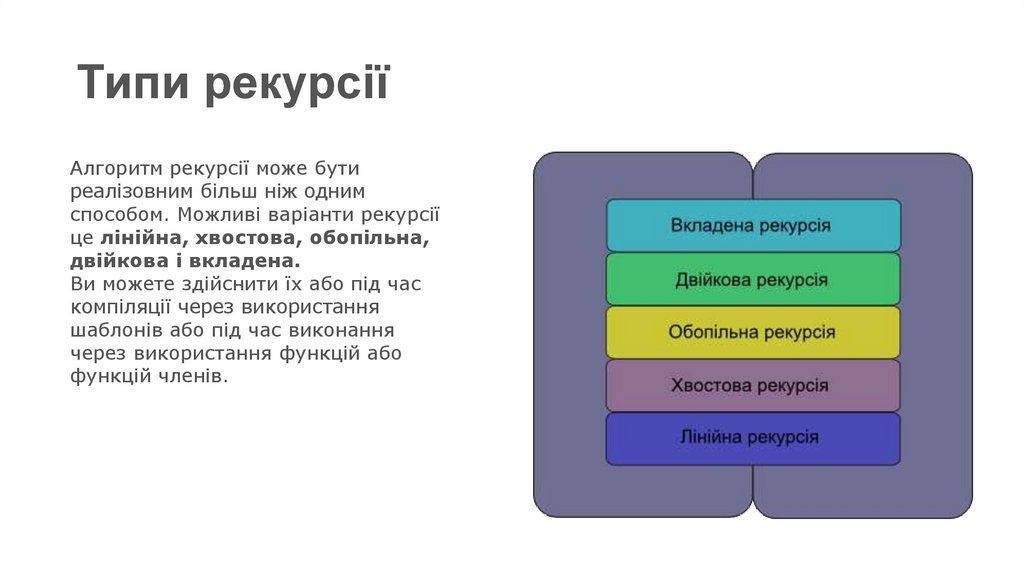
Лінійна рекурсія• Лінійна рекурсія - це найпростіший вид рекурсії і
можливо найуживаніша рекурсія. У цієї рекурсії, одна
функція просто викликає себе доти, доки не досягне
умови завершення (також відомої як базова умова);
цей процес відомий як намотування. Як тільки
виконана умова завершення, виконання програми
повертається до викликальника; це зветься
розмотуванням.
• Упродовж намотування і розмотування функція може
виконувати якісь додаткові корисні задачі; у випадку
факторіала вона множить вхідне значення на значення
повернуте під час фази розмотування. Цей процес
можна зобразити у вигляді такої діаграми (знизу), яка
показує обидві фази функції обчислення факторіала із
використанням лінійної рекурсії.
17.
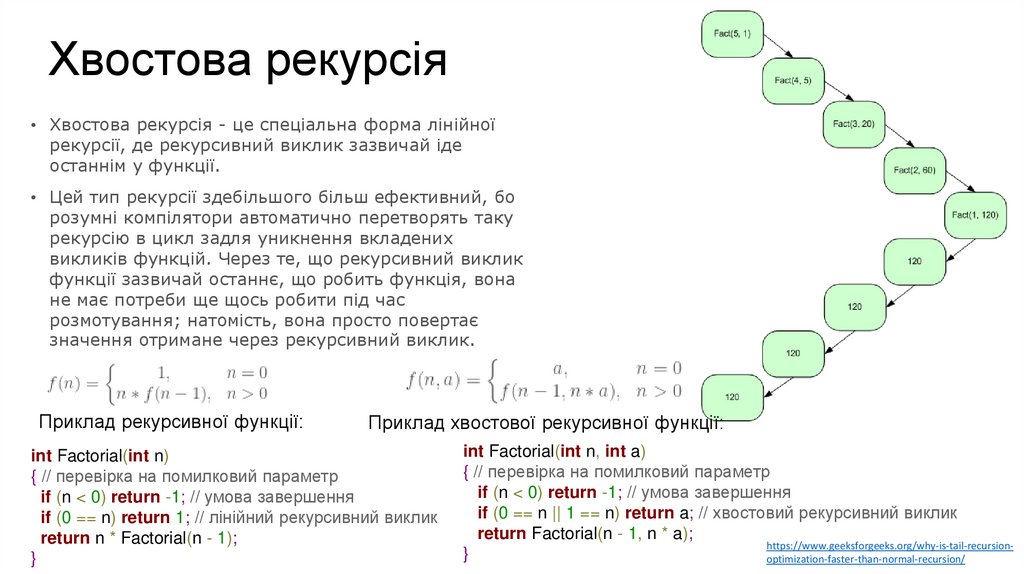
Хвостова рекурсія• Хвостова рекурсія - це спеціальна форма лінійної
рекурсії, де рекурсивний виклик зазвичай іде
останнім у функції.
• Цей тип рекурсії здебільшого більш ефективний, бо
розумні компілятори автоматично перетворять таку
рекурсію в цикл задля уникнення вкладених
викликів функцій. Через те, що рекурсивний виклик
функції зазвичай останнє, що робить функція, вона
не має потреби ще щось робити під час
розмотування; натомість, вона просто повертає
значення отримане через рекурсивний виклик.
Приклад рекурсивної функції:
Приклад хвостової рекурсивної функції:
int Factorial(int n)
{ // перевірка на помилковий параметр
if (n < 0) return -1; // умова завершення
if (0 == n) return 1; // лінійний рекурсивний виклик
return n * Factorial(n - 1);
}
int Factorial(int n, int a)
{ // перевірка на помилковий параметр
if (n < 0) return -1; // умова завершення
if (0 == n || 1 == n) return a; // хвостовий рекурсивний виклик
return Factorial(n - 1, n * a);
https://www.geeksforgeeks.org/why-is-tail-recursion}
optimization-faster-than-normal-recursion/
18.
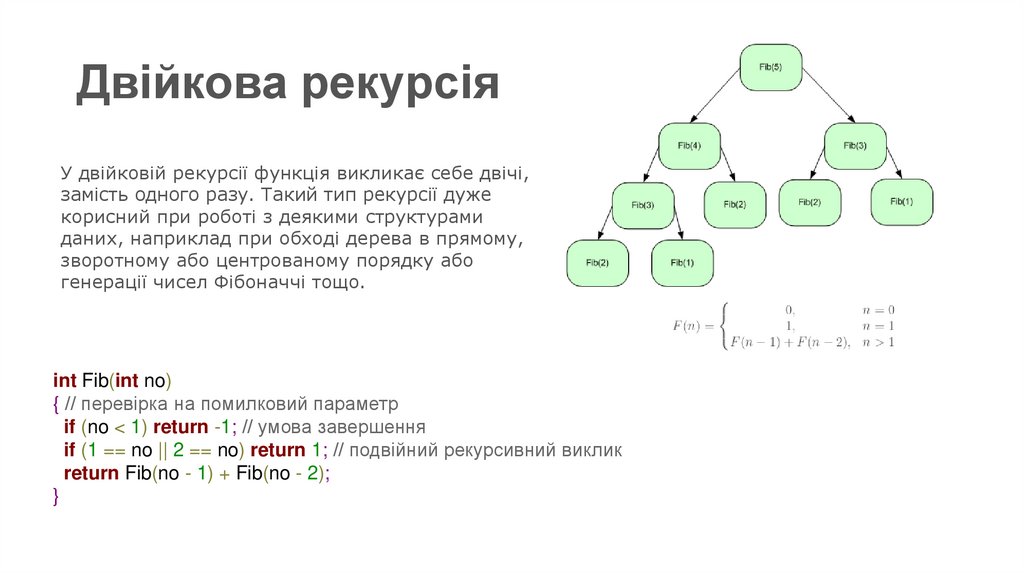
Двійкова рекурсіяУ двійковій рекурсії функція викликає себе двічі,
замість одного разу. Такий тип рекурсії дуже
корисний при роботі з деякими структурами
даних, наприклад при обході дерева в прямому,
зворотному або центрованому порядку або
генерації чисел Фібоначчі тощо.
int Fib(int no)
{ // перевірка на помилковий параметр
if (no < 1) return -1; // умова завершення
if (1 == no || 2 == no) return 1; // подвійний рекурсивний виклик
return Fib(no - 1) + Fib(no - 2);
}
19.
20.
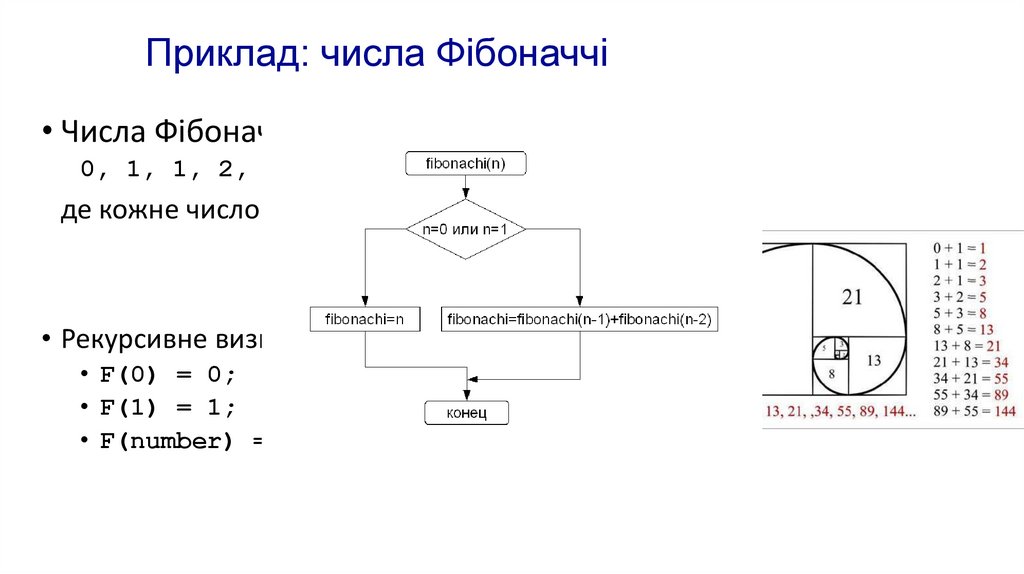
Приклад: числа Фібоначчі• Числа Фібоначчі:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ...
де кожне число дорівнює сумі двох попередніх чисел.
• Рекурсивне визначення:
• F(0) = 0;
• F(1) = 1;
• F(number) = F(number-1)+ F(number-2);
21.
Обчислення числа Фібоначчі ітеративно (без рекурсії):int fib(int n)
{
int f[100];
f[0] = 0; f[1] = 1;
for (int i=2; i<= n; i++)
f[i] = f[i-1] + f[i-2];
return f[n];
}
22.
23.
//Обчислити число Фібоначчі, використовуючи рекурсіюint fib(int number)
{
if (number == 0) return 0;
//зупинка unsigned
рекурсії
long long fib (unsigned short n)
if (number == 1) return 1;
//зупинка { рекурсії
if(n < 2) return n ;
else//виклики
return fib(n-1)функції
+ fib(n-2); з іншим параметром
return (fib(number-1) + fib(number-2));
}
}
int main(){
int inp_number;
cout << "Please enter an integer: ";
unsigned long long fib (unsigned short n)
{
return n < 2? n : fib(n-1) + fib(n-2);
}
cin >> inp_number;
cout<<"The Fibonacci number for "<< inp_number <<" is "<<fib(inp_number)<< endl;
return 0;
}
24.
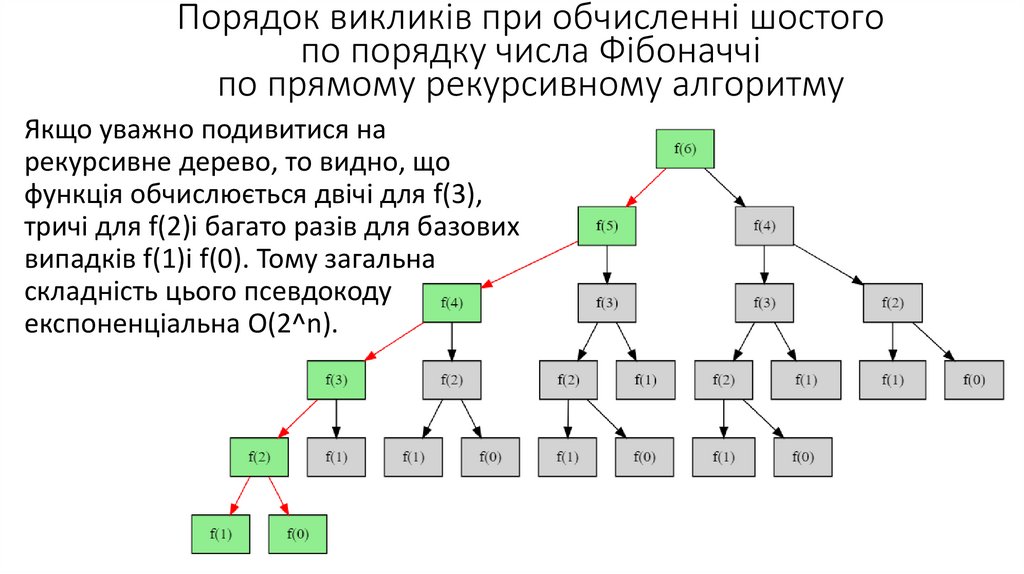
Порядок викликів при обчисленні шостогопо порядку числа Фібоначчі
по прямому рекурсивному алгоритму
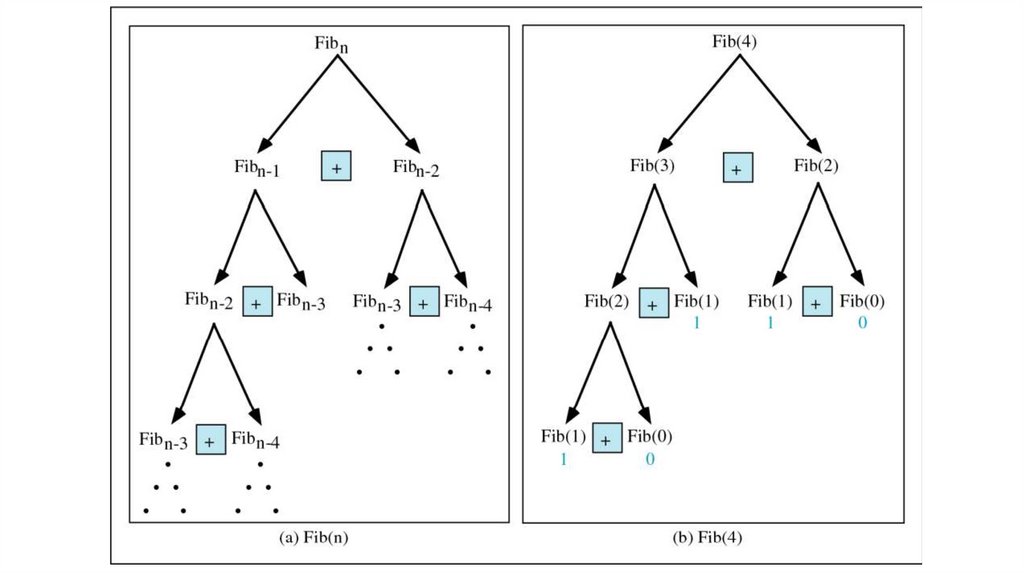
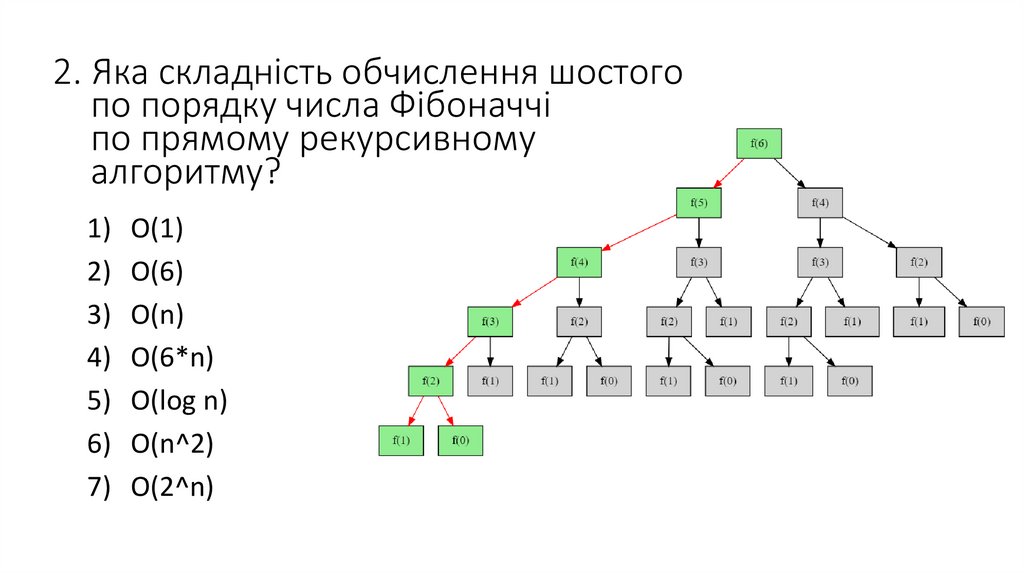
Якщо уважно подивитися на
рекурсивне дерево, то видно, що
функція обчислюється двічі для f(3),
тричі для f(2)і багато разів для базових
випадків f(1)і f(0). Тому загальна
складність цього псевдокоду
експоненціальна O(2^n).
25.
Порядок викликів при обчисленні шостогопо порядку числа Фібоначчі
по прямому рекурсивному алгоритму
• Отже, для обчислення кожного числа
Фібоначчі (крім двох перших) виконується два
виклики функції. Тобто. якщо нам знадобиться
обчислити, наступне (сьоме) число Фібоначчі,
кількість викликів практично подвоїться. І
справді, кожне наступне число обчислюється
вдвічі довше, ніж попереднє. За наявності
терпіння ще можна якось дочекатися кінця
обчислення 50-го числа, але далі
обчислюється дуже довго.
• В чому причина? Чому людина,
обчислюючи на папері,
легко обганяє комп'ютер?
• Звісно,
неефективний алгоритм.
26.
27.
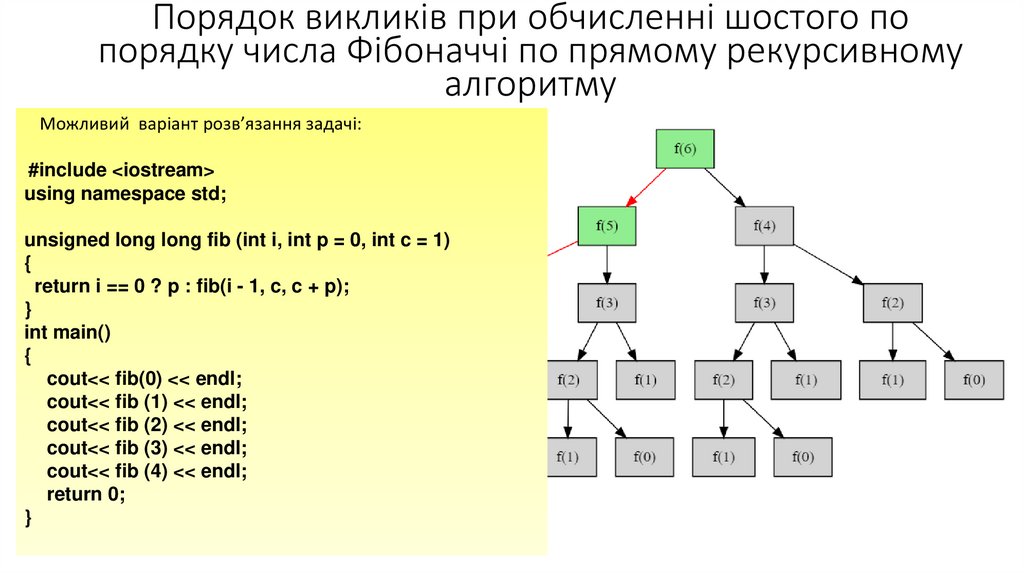
Порядок викликів при обчисленні шостого попорядку числа Фібоначчі по прямому рекурсивному
алгоритму
варіант
розв’язаннявиділені
задачі:
• Можливий
На малюнку
кольором
ті блоки,
обчислення яких справді необхідне. Число
таких блоків
зростає зі збільшенням номера
#include
<iostream>
числа
лінійноstd;
- O(n). А ось решта блоків using
namespace
суцільні повтори і їх число зростає як O(2n).
unsigned
long long
fib (int
i, int p = 0,так,
int c щоб
= 1) вона
• Спробуйте
змінити
програму
{ працювала швидко (без повторних
обчислень.
return
i == 0 ? p : fib(i - 1, c, c + p);
}• Як вправу, я попрошу
intНЕ
main()
використовувати циклів.
{
cout<< fib(0) << endl;
cout<< fib (1) << endl;
cout<< fib (2) << endl;
cout<< fib (3) << endl;
cout<< fib (4) << endl;
return 0;
}
28.
Вкладена рекурсія• Це особливий тип рекурсії, коли рекурсивні виклики вкладені. В усіх
попередніх типах рекурсії, ви можете замінити рекурсію на простий цикл
або цикл зі стеком, але цей тип рекурсії не може бути легко замінений на
простий цикл.
• Типовим прикладом вкладеної рекурсії є функція Акермана.
• Математично функція Акермана може бути визначена як
int Ackermann(int m, int n)
{ // перевірка параметрів
if (m < 0 || n < 0) return -1; // умова завершення
if (0 == m) return n + 1; // лінійний рекурсивний виклик
else
if (m > 0 && 0 == n) return Ackermann(m-1, 1); // вкладений рекурсивний виклик
else return Ackermann(m-1, Ackermann(m, n-1)); }
29.
РЕКУРСІЯ ЗСЕРЕДИНИЦе може здатися надзвичайним, але cамовиклик функції нічим не
відрізняється від виклику іншої функції. Що відбувається, якщо
одна функція викликає іншу? - Загалом наступне:
1) в пам'яті (стек) розміщаються аргументи, передані функції;
2) в іншому місці пам'яті зберігаються значення внутрішніх змінних
функції;
3) запам'ятовується адреса повернення до функції;
4) керування передається викликаній функції.
Якщо функцію викликати повторно з іншої функції або ж з неї
самої, буде виконуватися той самий код, але працювати він буде з
іншими значеннями аргументів і внутрішніх змінних. Це і дає
можливість рекурсії.
30.
Обопільна рекурсіяОбопільна рекурсія також відома як непряма рекурсія. В цьому типі рекурсії, дві або
більше функції викликають одна одну циклічно. Це єдиний шлях для здійснення
рекурсії в мовах, що не дозволяють вам викликати функції рекурсивно. Умова
завершення в такій рекурсії може бути в одній або всіх функціях.
bool isEven(int no)
{ // умова завершення
if (0 == no) return true;
else // взаємний рекурсивний виклик
return isOdd(no - 1);
}
bool isOdd(int no)
{ // умова завершення
if (0 == no) return false;
else // взаємний рекурсивний виклик
return isEven(no - 1);
}
https://harmyder.wordpress.com/2011/07/25/вступ-у-використання-рекурсії-в-c-част/
31.
Як написати рекурсивну функцію?32.
Приклад 1. x ^ yint pow(int x,int y)
{
if(y==0) return 1;
else return x*pow(x,y-1);
}
int main()
{ std::cout << "x ^ y = "<<pow(2,5);
}
33.
Приклад 2. Перевести натуральне число Z увiсiмкову систему числення
void Convert2(int Z)
void Convert8(int Z)
{
{
if (Z > 1) Convert2(Z / 2);
if (Z > 1) Convert8(Z / 8);
std::cout << Z % 2;
cout << Z % 8;
}
}
std::cout<<" 100 -> 8 = "; Convert8(100); std::cout<<std::endl;
Питання: Як перевести натуральне число Z у
двійкову систему числення? Є пропозиції?
34.
Приклад 3. Інверсія заданого рядка• 1 спосіб
1) інверсія порожнього рядка або
рядка, що складається з одного
символа, – це вихідний рядок. Тому,
якщо довжина рядка s є не більшою
від одого символа, то Inverse(s)
залишає рядок s без змін;
2) якщо довжина рядка s більша за 1,
то у вихідному рядку міняємо місцями
перший та останній символи та
викликаємо підпрограму Inverse для
підрядка s1, що є рядком s без
першого й останнього символів
void Inverse(char s[])
{
if (strlen(s) > 1)
{
char c_first[2], c_last[2], s1[strlen(s)];
/* у змінні c_first і c_ last копіюємо 1-ий і останній символи рядка s */
c_first[0] = s[0]; c_last[0] = s[strlen(s)-1]; c_first[1] = c_last[1] = '\0’;
/* у рядок s1 копіюємо рядок s без 1-го і останнього символів */
strncpy(s1, &s[1], strlen(s)-2); s1[strlen(s)-2] = '\0’;
Inverse(s1); // Рекурсивний виклик
strcpy(s, c_last);
strcat(s, s1);
strcat(s, c_first);
}
Цю рекурсивну підпрограму можна записати простіше,
}
якщо використати два додаткових формальних параметри,
char s[]="Hello world";
Inverse(s);
std::cout<<s<<std::endl;
які визначатимуть межі рядка (тобто з якого по який
символ), над яким потрібно проводити операцію
інвертування.
35.
Приклад 3. Інверсія заданого рядка• 2 спосіб
Тут два додаткових формальних
параметри визначають межі рядка,
тобто з якого по який символ
потрібно проводити операцію
інвертування
void Inverse(char s[], int l, int r)
{
char c;
if (l < r) // довжина рядка <= 1
{
c = s[l]; s[l] = s[r]; s[r] = c;
Inverse(s, l+1, r-1);
Єдиною незручністю, порівняно з попереднім прикладом, є те, що
}
початковий виклик підпрограми Inverse для рядка s має бути таким:
}
Inverse(s, 0, strlen(s)-1);
Проте цю незручність можна подолати, якщо описати іншу
підпрограму, що викликатиме підпрограму Inverse:
void Inv(char s[])
{
Inverse(s, 0, strlen(s)-1);
}
36.
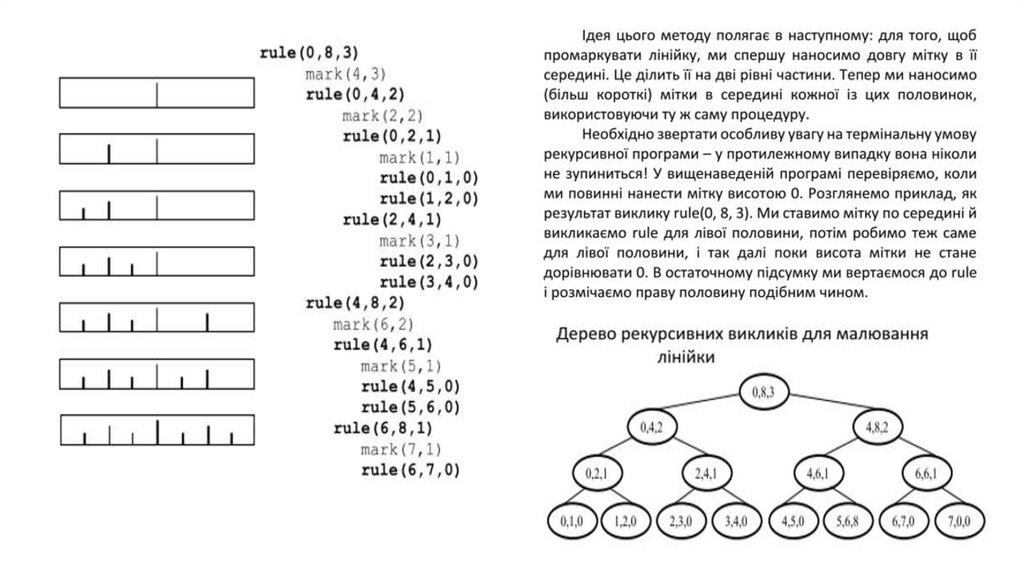
Приклад 4. Поділ навпіл37.
38.
39.
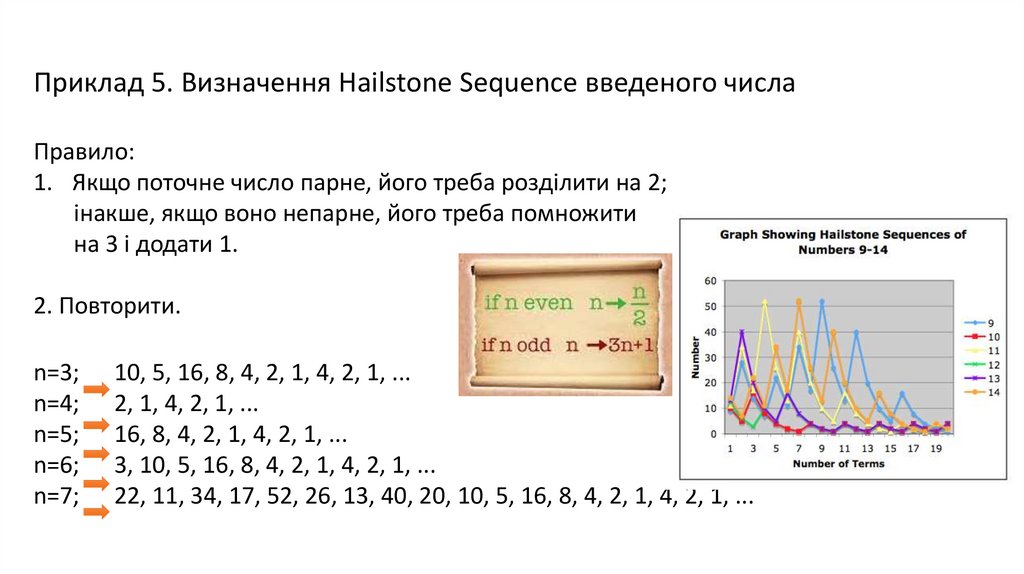
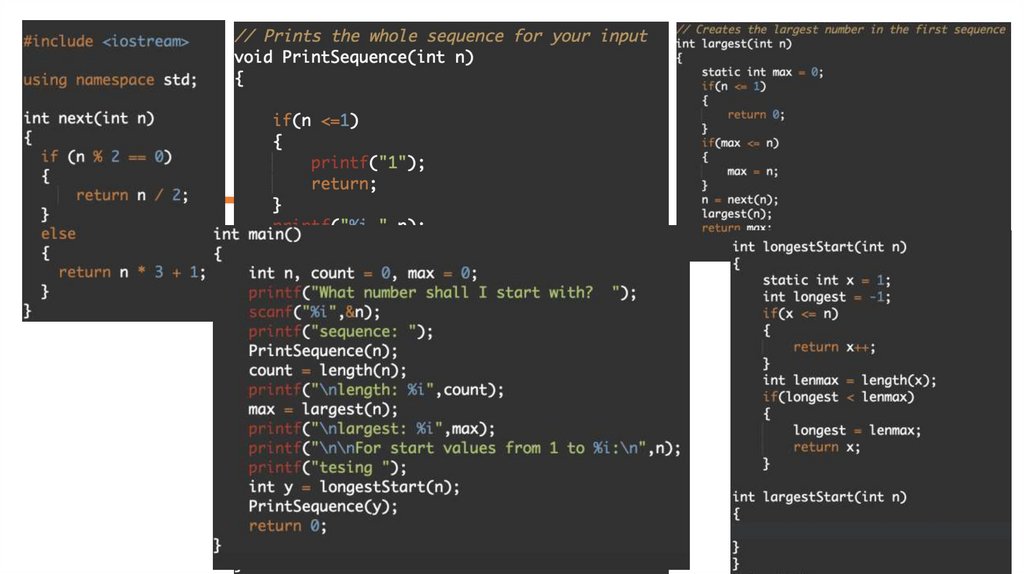
Приклад 5. Визначення Hailstone Sequence введеного числаПравило:
1. Якщо поточне число парне, його треба розділити на 2;
інакше, якщо воно непарне, його треба помножити
на 3 і додати 1.
2. Повторити.
n=3;
n=4;
n=5;
n=6;
n=7;
10, 5, 16, 8, 4, 2, 1, 4, 2, 1, ...
2, 1, 4, 2, 1, ...
16, 8, 4, 2, 1, 4, 2, 1, ...
3, 10, 5, 16, 8, 4, 2, 1, 4, 2, 1, ...
22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1, 4, 2, 1, ...
40.
Тестові дані:Введіть будь-яке натуральне число для Hailstone Sequence : 13
Очікуваний результат :
The hailstone sequence starting at 13 is : 13 40 20 10 5 16 8 4 2 1
The length of the sequence is 10.
З якого числа почати? 16
послідовність: 16 8 4 2 1
довжина: 5
найбільший: 16
Для початкових значень від 1 до 16:
найдовше: 9 28 14 7 22 11 34 17 52 26 13 40 20 10 5 16 8 4 2 1
довжина: 20
містить найбільший: 15 46 23 70 35 106 53 160 80 40 20 10 5 16 8 4 2 1
найбільший: 160
41.
42.
Гра Ханойська вежа# Recursive Python function to solve tower of hanoi
n - кількість дисків,
#include <bits/stdc++.h>
from_rod, to_rod, aux_rod - штирі
def
TowerOfHanoi(n,
from_rod,
to_rod, aux_rod):
using namespace std;
n == 0:
void if
towerOfHanoi(int
n, char from_rod, char to_rod, char aux_rod)
return
{
TowerOfHanoi(n-1,
from_rod, aux_rod, to_rod)
if
(n == 0) {
from_rod
return;
print("Move
disk", n, "from rod", from_rod, "to rod", to_rod)
}TowerOfHanoi(n-1, aux_rod, to_rod, from_rod)
towerOfHanoi(n - 1, from_rod, aux_rod, to_rod);
cout << "Move disk " << n << " from rod " << from_rod
# Driver code
<< " to rod " << to_rod << endl;
N = towerOfHanoi(n
3
- 1, aux_rod, to_rod, from_rod);
}
#
C, B are the name of rods
intA,main()
TowerOfHanoi(N, 'A', 'C', ‘B’)
{
int N = 3;
// A, B and C are names of rods
towerOfHanoi(N, 'A', 'C', 'B');
return 0;
}
to_rod
aux_rod
43.
44.
45.
46.
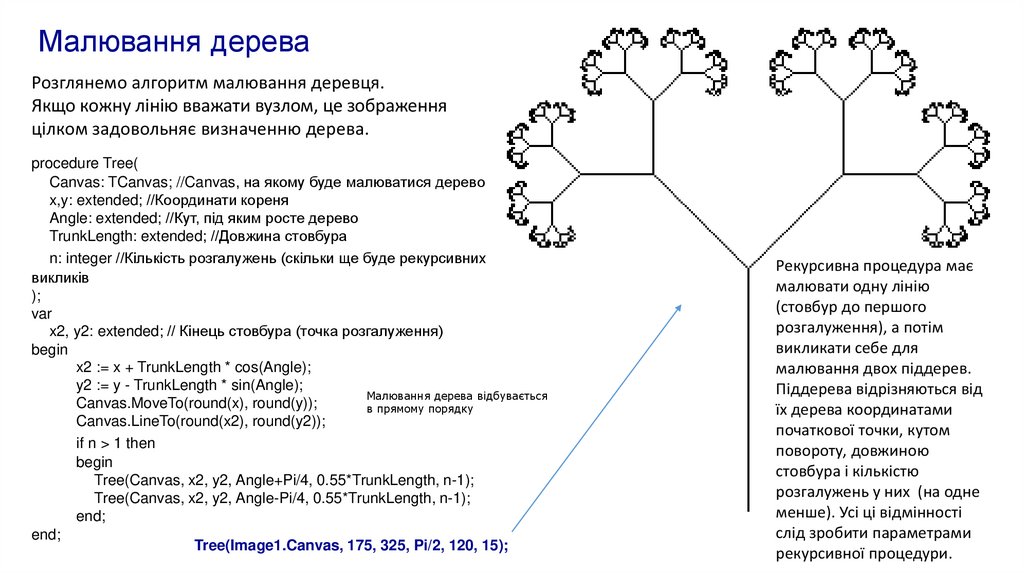
Малювання дереваРозглянемо алгоритм малювання деревця.
Якщо кожну лінію вважати вузлом, це зображення
цілком задовольняє визначенню дерева.
procedure Tree(
Canvas: TCanvas; //Canvas, на якому буде малюватися дерево
x,y: extended; //Координати кореня
Angle: extended; //Кут, під яким росте дерево
TrunkLength: extended; //Довжина стовбура
n: integer //Кількість розгалужень (скільки ще буде рекурсивних
викликів
);
var
x2, y2: extended; // Кінець стовбура (точка розгалуження)
begin
x2 := x + TrunkLength * cos(Angle);
y2 := y - TrunkLength * sin(Angle);
Малювання дерева відбувається
Canvas.MoveTo(round(x), round(y));
в прямому порядку
Canvas.LineTo(round(x2), round(y2));
if n > 1 then
begin
Tree(Canvas, x2, y2, Angle+Pi/4, 0.55*TrunkLength, n-1);
Tree(Canvas, x2, y2, Angle-Pi/4, 0.55*TrunkLength, n-1);
end;
end;
Tree(Image1.Canvas, 175, 325, Pi/2, 120, 15);
Рекурсивна процедура має
малювати одну лінію
(стовбур до першого
розгалуження), а потім
викликати себе для
малювання двох піддерев.
Піддерева відрізняються від
їх дерева координатами
початкової точки, кутом
повороту, довжиною
стовбура і кількістю
розгалужень у них (на одне
менше). Усі ці відмінності
слід зробити параметрами
рекурсивної процедури.
47.
48.
49.
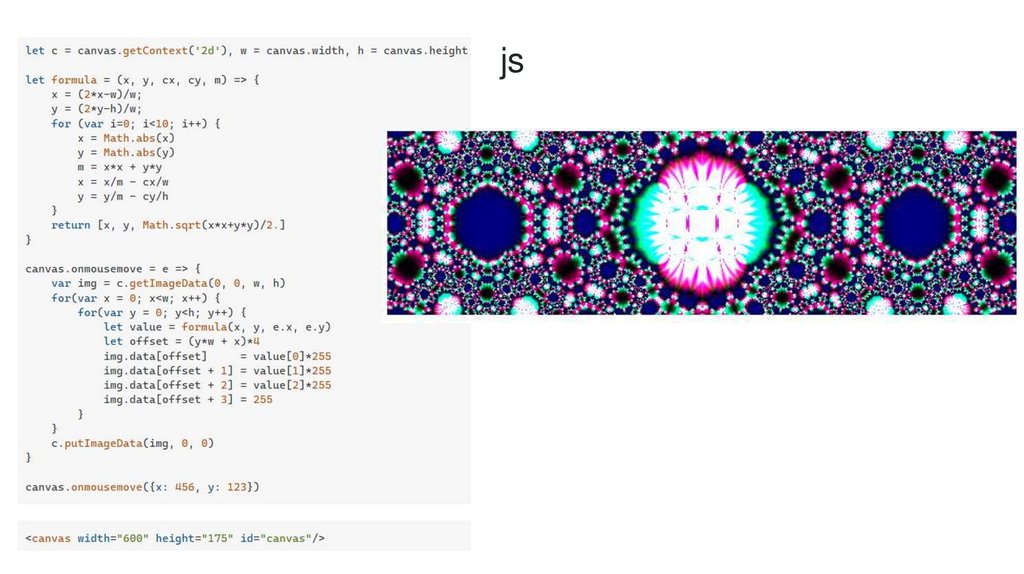
jslet c = canvas.getContext('2d'), w = canvas.width, h = canvas.height let
formula = (x, y, cx, cy, m) => { x = (2*x-w)/w; y = (2*y-h)/w; for (var i=0;
i<10; i++) { x = Math.abs(x) y = Math.abs(y) m = x*x + y*y x = x/m cx/w y = y/m - cy/h } return [x, y, Math.sqrt(x*x+y*y)/2.] }
canvas.onmousemove = e => { var img = c.getImageData(0, 0, w, h)
for(var x = 0; x<w; x++) { for(var y = 0; y<h; y++) { let value = formula(x,
y, e.x, e.y) let offset = (y*w + x)*4 img.data[offset] = value[0]*255
img.data[offset + 1] = value[1]*255 img.data[offset + 2] = value[2]*255
img.data[offset + 3] = 255 } } c.putImageData(img, 0, 0) }
canvas.onmousemove({x: 456, y: 123})<canvas width="600" height="175"
id="canvas"/>
50.
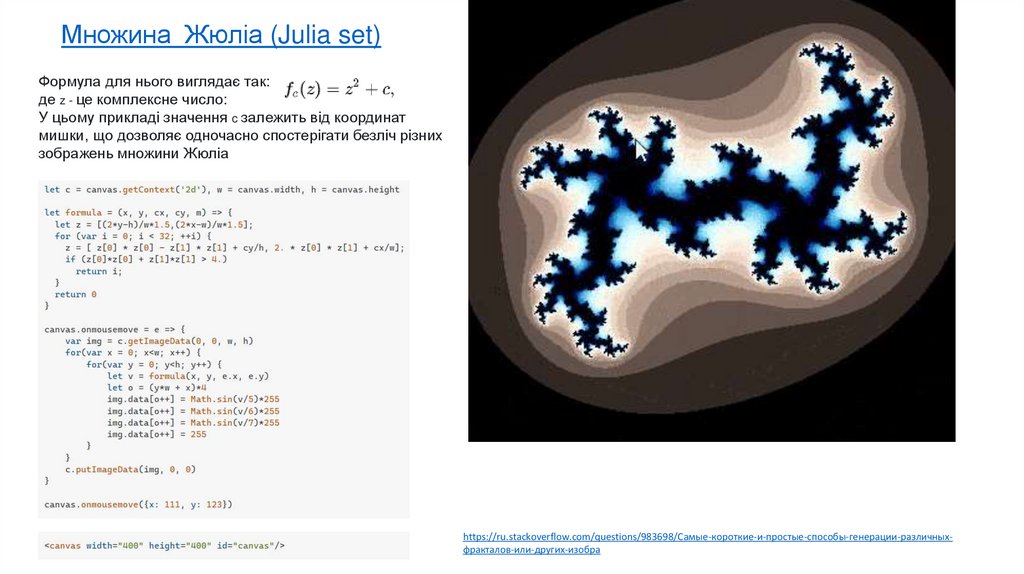
Множина Жюліа (Julia set)Формула для нього виглядає так:
де z - це комплексне число:
У цьому прикладі значення c залежить від координат
мишки, що дозволяє одночасно спостерігати безліч різних
зображень множини Жюліа
let c = canvas.getContext('2d'), w =
canvas.width, h = canvas.height let formula =
(x, y, cx, cy, m) => { let z = [(2*y-h)/w*1.5,(2*xw)/w*1.5]; for (var i = 0; i < 32; ++i) { z = [ z[0]
* z[0] - z[1] * z[1] + cy/h, 2. * z[0] * z[1] +
cx/w]; if (z[0]*z[0] + z[1]*z[1] > 4.) return i; }
return 0 } canvas.onmousemove = e => { var
img = c.getImageData(0, 0, w, h) for(var x = 0;
x<w; x++) { for(var y = 0; y<h; y++) { let v =
formula(x, y, e.x, e.y) let o = (y*w + x)*4
img.data[o++] = Math.sin(v/5)*255
img.data[o++] = Math.sin(v/6)*255
img.data[o++] = Math.sin(v/7)*255
img.data[o++] = 255 } } c.putImageData(img, 0,
0) } canvas.onmousemove({x: 111, y:
123})<canvas width="400" height="400"
id="canvas"/>
https://ru.stackoverflow.com/questions/983698/Самые-короткие-и-простые-способы-генерации-различныхфракталов-или-других-изобра
51.
52.
53.
54.
https://uk.javascript.info/recursionhttp://programming.in.ua/programming/c-plus-plus/313-recursion-c-plus-plus.html
55.
РЕКУРСИВНІ СТРУКТУРИ ДАНИХСтек можна визначити рекурсивно:
1. Порожній стек.
2. Верхівка стека; стек
Чергу можна визначити рекурсивно:
1. Порожня черга.
2. Перший елемент; черга.
Класичний список можна визначити рекурсивно:
1. Порожній список.
2. Перший елемент; список
Кільцевий список можна визначити рекурсивно:
1. Порожній список.
2. Список; поточний елемент; список.
// Рекурсивна підпрограма
// виведення списку на екран
void ShowList(list l)
{
if (!empty(l))
{
cout << head(l) << " ";
ShowList(tail(l));
}
}
56.
Контрольні запитання1. Яку функцію визначає такий запис?
1) умовну для визначення числа (n-1)
2) розгалужену для добутку n*(n-1)
3) лінійну для добутку n*(n-1)
4) рекурсивну для n!
5) циклічну для n!
6) асимптотичну
57.
2. Яка складність обчислення шостогопо порядку числа Фібоначчі
по прямому рекурсивному
алгоритму?
1) О(1)
2) O(6)
3) O(n)
4) O(6*n)
5) O(log n)
6) O(n^2)
7) O(2^n)
58.
3. Яка помилка цього програмного коду?int fac(int numb){
return numb * fac(numb-1);
}
1) Помилки немає
2) Потрібен цикл
3) Невідповідність типів
4) Нескінченний ланцюжок викликів функцій
59.
4. Яка помилка цього програмного коду?int fac(int numb){
if (numb<=1)
return 1;
else
return numb * fac(numb+1);
}
1) Помилки немає
2) Потрібен цикл
3) Невідповідність типів
4) Нескінченний ланцюжок викликів функцій
60.
5. Яка типи рекурсії існують?1) лінійна
2) умовна
3) циклічна
4) хвостова
5) обопільна
6) двійкова
7) вкладена
8) стекова
61.
6. Який це тип рекурсії?1) лінійна
2) умовна
3) циклічна
4) хвостова
5) обопільна
6) двійкова
7) вкладена
8) стекова
int Factorial(int n)
{
if (n < 0) return -1;
if (0 == n) return 1;
return n * Factorial(n - 1);
}
62.
7. Який це тип рекурсії?1) лінійна
2) умовна
3) циклічна
4) хвостова
5) обопільна
6) двійкова
7) вкладена
8) стекова
int Factorial(int n, int a)
{if (n < 0) return -1;
if (0 == n || 1 == n) return a;
return Factorial(n - 1, n * a);
}
63.
8. Який це тип рекурсії?1) лінійна
2) умовна
3) циклічна
4) хвостова
5) обопільна
6) двійкова
7) вкладена
8) стекова
int Fib(int no)
{
if (no < 1) return -1;
if (1 == no || 2 == no) return 1;
return Fib(no - 1) + Fib(no - 2);
}
64.
9. Який це тип рекурсії?1) лінійна
2) умовна
3) циклічна
4) хвостова
5) обопільна
6) двійкова
7) вкладена
8) стекова
bool isEven(int no)
{
if (0 == no) return true;
else
return isOdd(no - 1);
}
bool isOdd(int no)
{
if (0 == no) return false;
else
return isEven(no - 1);
}















































 Программирование
Программирование