Тема 1. Теоретические основы стрельбы ЗУР. Занятие 1. Закон ошибок стрельбы ЗУР

1.

2. 1. Показатели эффективности стрельбы ЗУР

3.

Стрельба ЗУР - это процесс боевой работы расчета боевой машины (батареи),
направленный на выполнение поставленной огневой задачи.
Стрельба ЗУР начинается с момента постановки огневой задачи батарее (БМ)
на уничтожение цели и заканчивается окончанием оценки результатов
обстрела и состоит из подготовки обстрела, обстрела цели и оценки
результатов обстрела.
Задачи стрельбы
Поражение
одиночной
цели
Уничтожение
возможно большого
числа самолетов
в составе групповой цели

4.

Задачи стрельбы
Уничтожение возможно
большого числа самолетов
в составе групповой цели
Поражение
одиночной цели
Вероятность поражения
одиночной цели
одной ракетой
R1
Математическое ожидание
числа пораженных целей
Mn
ПЭС
Вероятность поражения
одиночной цели
очередью из n-ракет
Rn
ПЭС

5.

Боевой эффективностью ЗРК называется степень соответствия результатов
боя батареи (БМ), поставленной боевой задаче по отражению конкретного
удара средств воздушного нападения (СВН). Боевая эффективность ЗРК
зависит главным образом от временных характеристик комплекса, размеров
зоны поражения, параметров налета и слаженности боевых расчетов.
Задачи стрельбы
Поражение
одиночной
цели
Выполнить
огневую
задачу
Уничтожение
возможно большого
числа самолетов
в составе
групповой цели

6.

Задачи
стрельбы
Поражение
одиночной
цели
Вероятность
поражения
одиночной цели
одной ракетой
R1
ПБЭ
Вероятность
поражения
одиночной цели
очередью из n-ракет
Rn
Выполнить
огневую
задачу
Уничтожение
возможно большого
числа самолетов
в составе
групповой цели
Вероятность
выполнения
огневой задачи
Pог.з.
Математическое
ожидание числа
пораженных целей
Mn
ПБЭ
ПБЭ

7. 2. Модель поражения цели

8.

Модель поражения цели
Наведение
(ЗОН)

9.

Модель поражения цели
Наведение
(ЗОН)
Подрыв
(ЗСРв)

10.

Модель поражения цели
Наведение
(ЗОН)
Подрыв
(ЗСРв)
Ущерб
(КЗПЦ)

11.

Модель поражения цели
Наведение
(ЗОН)
Подрыв
(ЗСРв)
Ущерб
(КЗПЦ)
Поражение
цели

12.

Модель поражения цели
Наведение
(ЗОН)
Подрыв
(ЗСРв)
Ущерб
(КЗПЦ)
Поражение
цели

13.

Для получения выражения вероятности поражения цели одной ракетой введем
прямоугольную систему координат
Y
Vp
P
dy
dx
Vp
Vо т н
y
P
Vц
OH
OC
x
O
X
z
Z
За начало координат (точка О) принимаем центр масс цели.
Ось ОХ направлена вдоль вектора относительной скорости сближения ракеты и цели.
Оси OY и OZ лежат в плоскости, перпендикулярной вектору скорости ракеты, и образуют
так называемую картинную плоскость.
Такая система координат позволяет рассматривать цель как неподвижный объект,
относительно которого ракета движется со скоростью Vотн.
Координаты точек разрыва x,y,z являются случайными величинами. Они характеризуют
ошибки стрельбы. Если разрыв боевой части ракеты произошел в точке с
координатами x,y,z то существует некоторая вероятность поражения цели, зависящая
от координат x,y,z.

14.

Поражение цели ЗУР можно представить в виде сложного случайного события,
состоящего из двух случайных событий, происходящих последовательно:
• разрыв боевой части ракеты в точке с координатами x,y,z относительно цели;
• поражение цели элементами боевой части ракеты при условии разрыва ее в точке с
координатами x,y,z.
Первое случайное событие характеризуется плотностью распределения координат точек
разрыва ракет относительно цели f(x,y,z), которая называется законом ошибок
стрельбы.
Второе случайное событие характеризует вероятность поражения цели в зависимости от
координат точек разрыва боевой части ракеты, т.е. функцией G(x,y,z), которая
называется координатным законом поражения цели.
Вероятность разрыва ракеты в строго определенной точке пространства практически
равна нулю. Поэтому вероятность первого события будем характеризовать вероятностью
разрыва ракеты в элементарном объеме dxdydz около точки x,y,z, т.е. величиной
f(x,y,z)dxdydz.
Вероятность сложного события dR
dR=f(x,y,z)dxdydz G(x,y,z)
В соответствии с законом ошибок стрельбы разрыв боевой части ракеты может
произойти в любой точке пространства относительно цели. Следовательно, для
определения вероятности поражения одиночной цели одной ракетой необходимо
применить формулу полной вероятности, интегрируя по всему объему пространства в
пределах от минус бесконечности до плюс бесконечности:
R1 =
f ( x , y , z ) G ( x , y , z ) dxdydz

15.

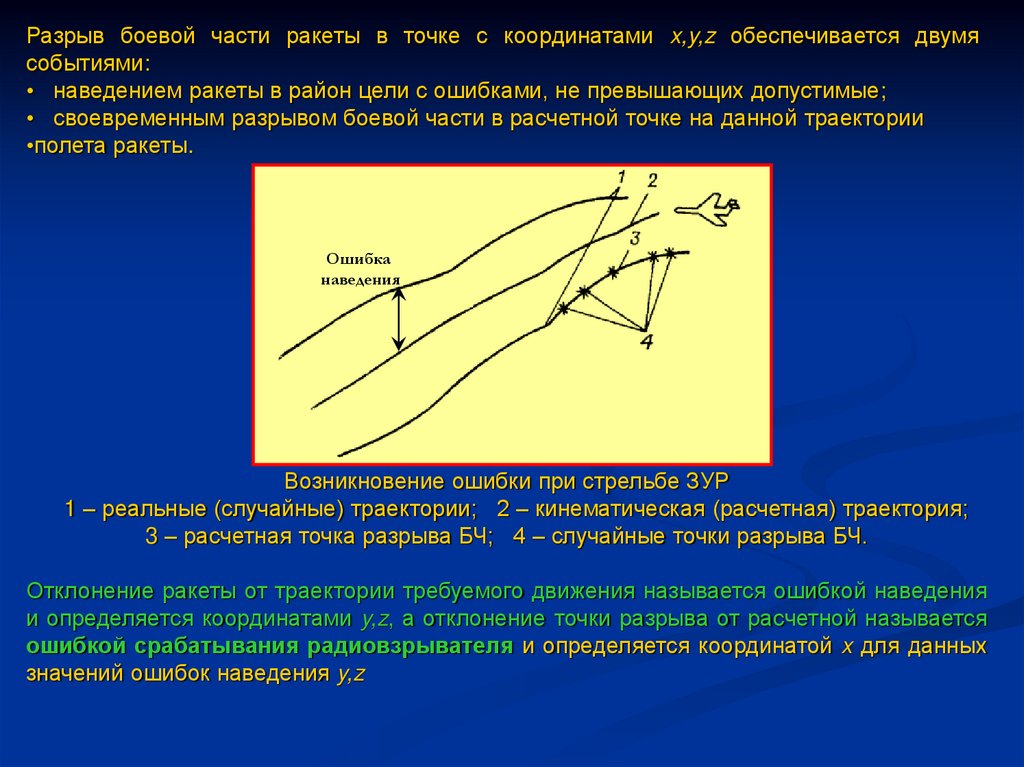
Разрыв боевой части ракеты в точке с координатами x,y,z обеспечивается двумя
событиями:
• наведением ракеты в район цели с ошибками, не превышающих допустимые;
• своевременным разрывом боевой части в расчетной точке на данной траектории
•полета ракеты.
Ошибка
наведения
Возникновение ошибки при стрельбе ЗУР
1 – реальные (случайные) траектории; 2 – кинематическая (расчетная) траектория;
3 – расчетная точка разрыва БЧ; 4 – случайные точки разрыва БЧ.
Отклонение ракеты от траектории требуемого движения называется ошибкой наведения
и определяется координатами y,z, а отклонение точки разрыва от расчетной называется
ошибкой срабатывания радиовзрывателя и определяется координатой x для данных
значений ошибок наведения y,z

16.

Таким образом, закон ошибок стрельбы можно представить в следующем виде:
f(x,y,z) = f(y,z) f(x/y,z)
где
f(y,z) – закон ошибок наведения.
f(x/y,z) – закон срабатывания радиовзрывателя.
В свою очередь закон срабатывания радиовзрывателя f(x/y,z) можно представить в виде:
f(x/y, z) = f1 (х/у, z) Р рв(y, z)
где f1(х/y, z) условная плотность распределения координаты х точек срабатывания
радиовзрывателя при заданных ошибках наведения у, z;
Р рв (y, z) условная вероятность срабатывания радиовзрывателя.
Введем понятие условного координатного закона поражения цели, которое имеет вид:
G(y,z) =G(x,y,z) f1(x/y,z) dx
Функция G(y,z) характеризует вероятность поражения цели в зависимости от ошибок
наведения ракеты на цель при условии согласования радиовзрывателя с боевой частью,
которое обеспечивается в ЗРК применением специальных мер. Эти меры ведут к тому,
что реальный разброс координаты x точек подрыва боевой части вдоль траектории
незначителен. Поэтому вероятность поражения цели одной ракетой можно считать
независимой от координаты x точек разрыва боевой части вдоль траектории.
Учитывая это получим:
R1 = f ( y , z ) G ( y , z ) Pрв ( y , z ) dydz
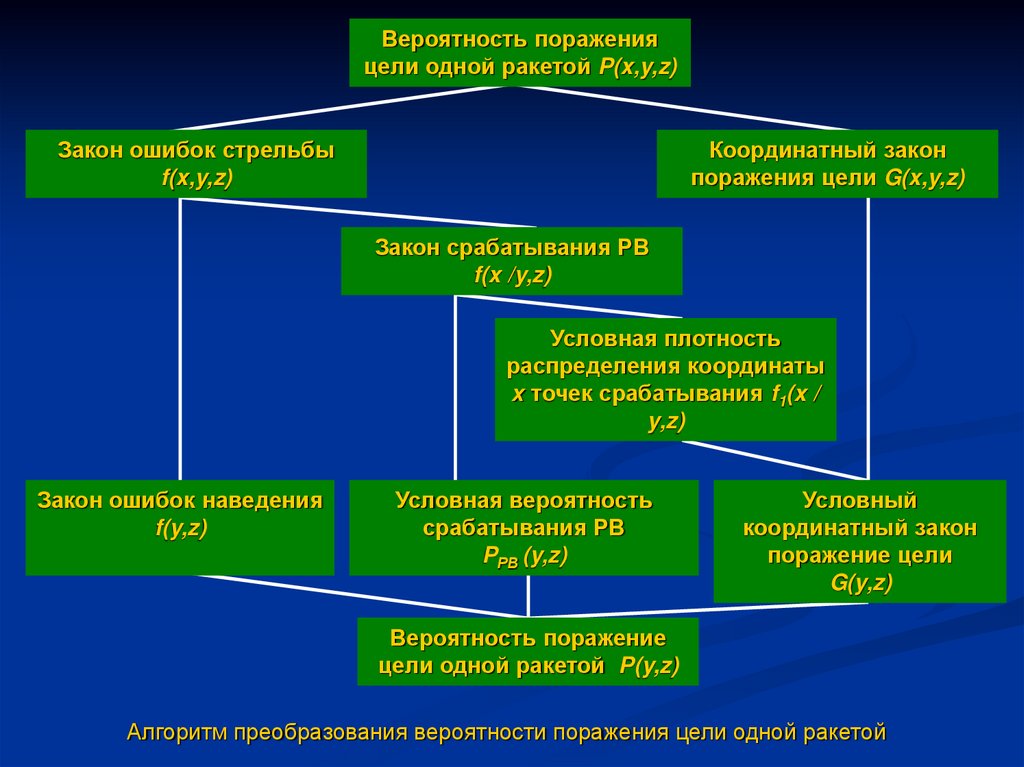
Таким образом получаем алгоритм преобразования трехмерной функции вероятности
поражения одиночной цели одной ракетой, в двумерную функцию:

17.

Вероятность поражения
цели одной ракетой P(x,y,z)
Закон ошибок стрельбы
f(x,y,z)
Координатный закон
поражения цели G(x,y,z)
Закон срабатывания РВ
f(x /y,z)
Условная плотность
распределения координаты
х точек срабатывания f1(x /
y,z)
Закон ошибок наведения
f(y,z)
Условная вероятность
срабатывания РВ
PРВ (y,z)
Условный
координатный закон
поражение цели
G(y,z)
Вероятность поражение
цели одной ракетой P(y,z)
Алгоритм преобразования вероятности поражения цели одной ракетой

18.

Закон ошибок
стрельбы ЗУР
Закон ошибок
стрельбы
Закон
срабатывания
радиовзрывателя

19. 3. Закон ошибок наведения ЗУР

20.

На ракету во время ее полета воздействует большое число факторов. Под
воздействием этих факторов ракета отклоняется от расчетной траектории. Все факторы
действуют одновременно. Поэтому ошибку, характеризуемую их воздействием, называют
суммарной ошибкой наведения.
Суммарная ошибка
наведения
Систематическая
составляющая
m
Случайная
составляющая
σ
Систематической составляющей суммарной ошибки наведения называют такую
ошибку, которая в процессе наведения остается постоянной или изменяется по вполне
определенному закону.
Случайной составляющей суммарной ошибки наведения называют такую
ошибку, которая от измерения к измерению может принять любое неизвестное заранее
по величине и знаку значение.

21.

По источникам возникновения ошибки наведения делятся на:
Суммарная
ошибка
наведения
Динамическая
Флюктуационная
Инструментальная
Личная
Каждый из источников этих ошибок дает систематическую и случайную
составляющие. Исключение составляет флюктуационная ошибка, которая не имеет
систематической составляющей.
Ошибкой наведения ЗУР называется радиус-вектор, проведенный в проекцию точки
разрыва ракеты на картинную плоскость.
Суммарный закон ошибок наведения может выражаться формулой:
f ( y, z) =
1
2ps ys z
.e
2
( z mz ) 2
1 ( y my )
+
2 s y2
s z2
Такую форму закона принято называть суммарным законом ошибок наведения в
главных осях рассеивания.
В ряде случаев, когда σy σz = σ, для упрощения аналитических выражений
переходят к круговому закону.
f ( y, z) =
1
2ps
.e
2
( y m y ) 2 + ( z mz ) 2
2s 2
Такой вид закона принято называть круговым суммарным законом ошибок
наведения.

22.

Y
Y
sy
my
m
s
Р
Y
sz
r
Z
Z
Z
mz
Промахом r называется случайный вектор между целью и проекцией точки разрыва
ракеты (Р) на картинную плоскость. Он характеризуется величиной промаха r и его
ориентацией в картинной плоскости - углом , т.е. проекция точки разрыва в картинной
плоскости может быть определена полярными координатами r и .
От кругового суммарного закона ошибок наведения выраженного перейдем к закону
распределения промахов ракеты (r). Он может быть описан формулой:
f (r) =
r
s2
r2
e 2s
2
Это выражение называется законом Релея.
Для комплекса «Оса-АКМ» при стрельбе по прямолинейно летящей цели среднее
квадратическое отклонение находится в пределах 3-7 метров.

23.

При стрельбе наибольший интерес представляет вычисление вероятности
наведения ракеты в круг заданного радиуса.
Пусть радиус круга, вероятность наведения в который необходимо определить, равен
r0 (называется радиус надежного срабатывания радиовзрывателя). Тогда при
отсутствии систематической составляющей ошибки наведения (m = 0) вероятность
наведения ЗУР в круг радиуса r0 может быть определена по следующей формуле:
r02
2 s2
=
P( r r0 ) 1 e
При наличии систематической составляющей суммарной ошибки наведения
функция плотности распределения промахов будет зависеть и от аргумента m. И
выражение для вероятности наведения в круг заданного радиуса можно выразить
формулой:
rо
P( r r0 ) =
0
r
s2
e
r 2 + m2
2s 2 I
rm
0 2 dr
s
где r – текущее значение промаха;
m – систематическая составляющая ошибки наведения (математическое ожидание
ошибки наведения);
s – среднее квадратическое отклонение случайной составляющей суммарной
ошибки наведения при круговом рассеивании траекторий;
rm
I0 2 – функция Бесселя первого рода нулевого порядка от мнимого аргумента.
s

24.

Интеграл в этом выражения в конечном виде не берется и вычисляется методами
численного интегрирования. Поэтому вероятность наведения ЗУР в круг радиуса r0 при
наличии систематической ошибки наведения определяется на практике с помощью
таблиц или графиков функции
m2
r2
r0
2s 2
2s 2
r
F ( r0* ,m* ) = e
s2 e
0
где
r
m
r0* = 0 ; m * = .
s
s
rm
I 0 2 dr
s

25. 4. Закон срабатывания радиовзрывателя

26.

Под областью срабатывания радиовзрывателя понимается пространственная
область около ракеты, определяемая геометрическим местом условных центров цели в
момент срабатывания РВ.
Закон срабатывания радиовзрывателя f(x/y,z) можно представить в виде:
f(x/y, z) = f1 (х/у, z) Р рв(y, z),
где f1(х/y, z) условная плотность распределения координаты х точек срабатывания
радиовзрывателя при заданных ошибках наведения у, z;
Р рв (y, z) условная вероятность срабатывания радиовзрывателя.
Координаты любой точки пространства могут быть выражены в полярной системе
координат r, , . Поэтому:
f ( / r , q ) = f 1 ( / r , q ) P PB ( r , q ),
где угол срабатывания радиовзрывателя. Он образован продольной осью ракеты
и линией ракета цель в момент срабатывания радиовзрывателя;
r случайное значение промаха в плоскости У р О р Z р ;
q – угол, определяющий ориентацию промаха в плоскости Ур Ор Zр
относительно оси О р Z р.
Yp
r
Dрв
Θ
Θ
Xp
Zp

27.

Конструктивно радиовзрыватели выполнены так, что распределение
срабатывания не зависит от ориентации промаха, т. е. от угла q. Поэтому:
их
углов
f( /r) = f1( /r) Р рв(r)
где f1( /r) условная плотность распределения углов срабатывания радиовзрывателя;
Р рв(r) условная вероятность срабатывания радиовзрывателя или вероятность того, что
радиовзрыватель сработает, если ракета пройдет относительно цели с промахом r.
Таким образом, законом срабатывания радиовзрывателя называется произведение
условной плотности распределения углов срабатывания радиовзрывателя на условную
вероятность его срабатывания.
Рассмотрим условную плотность распределения углов срабатывания РВ.
( m )2
1
f1( / r ) =
exp
2
2 s
2p s
где: m - математическое ожидание углов срабатывания РВ при заданных значениях
промаха r (для РВ 9Э316 по цели типа МИГ-19 m =62о);
s - СКО углов срабатывания при заданных r. (для РВ 9Э316 s =1,5о – 8о).
Угол является случайной величиной, принимающий при каждом пуске определенное
значение под действием большого числа случайных и неслучайных факторов,
важнейшими из которых являются:
- угол наклона ДН приемной антенны;
- случайный характер сигналов, отраженных от цели, обусловленный флуктуацией
сигналов и разнообразием ЭПР различных целей (локация в ближней зоне);
- относительной скорости сближения ракеты с целью;
- случайный характер действия радиопомех на частоте РВ.

28.

Вид функции Р РВ(r) зависит от конструкции радиовзрывателя и от соотношения между
ошибками наведения и максимальными значениями дальности Д РВ max и радиуса r РВ max
срабатывания радиовзрывателя.
Между Д РВ max и r РВ max существует следующая зависимость:
rPB max(min) = DPB max sin(m 3s )
Знак «+» соответствует rРВ max , а знак «-» - rРВ min . Под rРВ max здесь понимают такое
максимальное значение промаха, начиная с которого возможно срабатывание
радиовзрывателя для данного фиксированного значения ДРВmax при заданных m и s

29.

Условная вероятность
срабатывания РВ
зависит от
Величина
промаха
Чувствительность
приемника РВ
факторов
Мощность
передатчика
РВ
ЭОП цели
Флюктуация
отраженного
от цели сигнала

30.

Вероятность срабатывания РВ характеризуется случайной величиной промаха r и
хорошо аппроксимируется зависимостью вида:
( r m r )2
PPB ( r ) = 1 Ф̂
где
s r2
- нормальная функция распределения
Ф̂
m и s - математическое ожидание и дисперсия радиуса срабатывания РВ.
r
r
Обычно для характеристики функции РРВ(r) используют математическое ожидание
радиуса срабатывания радиовзрывателя, равное значению промаха, при котором
РРВ(r) = 0,9. Обозначим его через r0 и будем называть радиусом надежного
срабатывания
радиовзрывателя.
Тогда
реальную
функцию
РРВ(r)
можно
аппроксимировать ступенчатой кривой вида:
1 при r ro
Pрв (r ) =
0 при r > r0 .
Радиолокационный взрыватель 9Э316М-1 ракеты 9М33М3 обеспечивает неконтактный
подрыв БЧ вблизи цели в момент, обеспечивающий наиболее эффективное поражение
цели.