Применение производной к исследованию функции

1.

2.

Cлово “функция” (от латинского functio совершение, выполнение) впервые было
употреблено немецким математиком
В. Лейбницем в 1673г.
Под функцией Лейбниц понимал отрезок,
длина которого меняется по какому-нибудь
определенному закону.
y = f(x)
Лейбниц ввел также термины “переменная” и
“константа”.

3.

Лейбниц Готфрид Вильгельм
(1646-1716 гг.)
Немецкий математик, физик,
философ, изобретатель, историк,
языковед. В математике его
важнейшей заслугой является
создание дифференциального и
интегрального исчисления.
Разработал правила
дифференцирования, дал
определения экстремальных точек и
точек перегиба.

4.

Ньютон Исаак
(1643-1727 гг.)
Английский физик,
математик, механик и астроном.
Одновременно с Лейбницем, но
независимо от него, разработал
дифференциальное и интегральное
исчисления.

5.

6.

7.

Возрастающая функция
y
f (x) возрастает
0
x

8.

Убывающая функция
y
x
0
f (x) убывает

9.

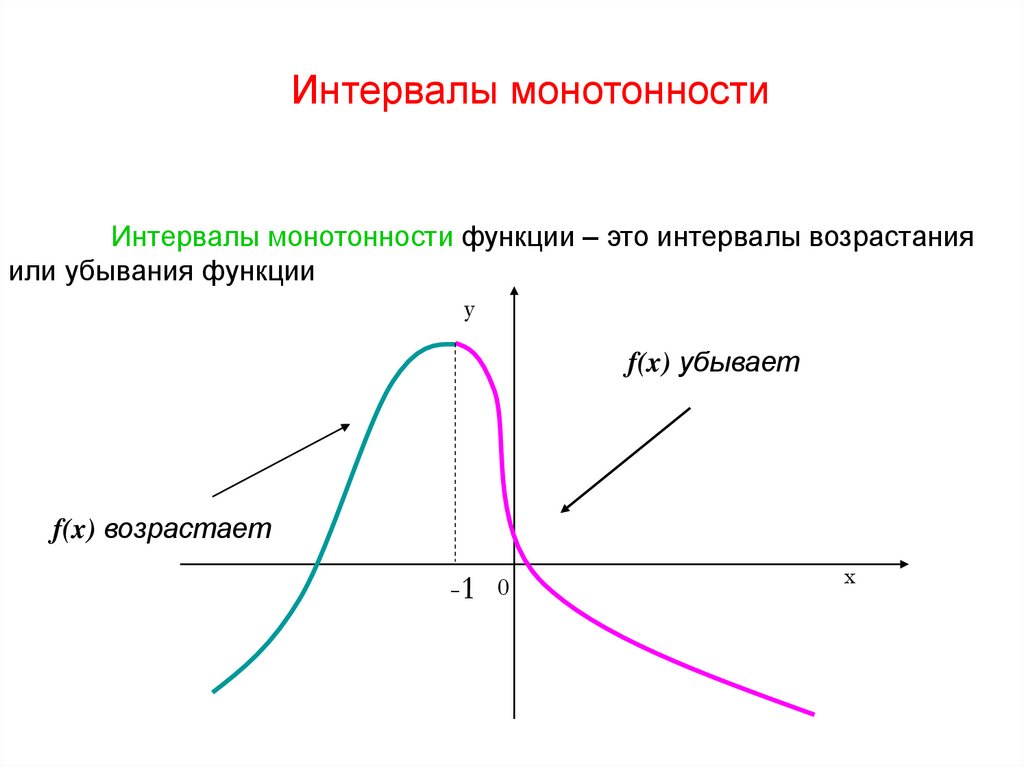
Интервалы монотонности
Интервалы монотонности функции – это интервалы возрастания
или убывания функции
y
f(x) убывает
f(x) возрастает
-1 0
x

10.

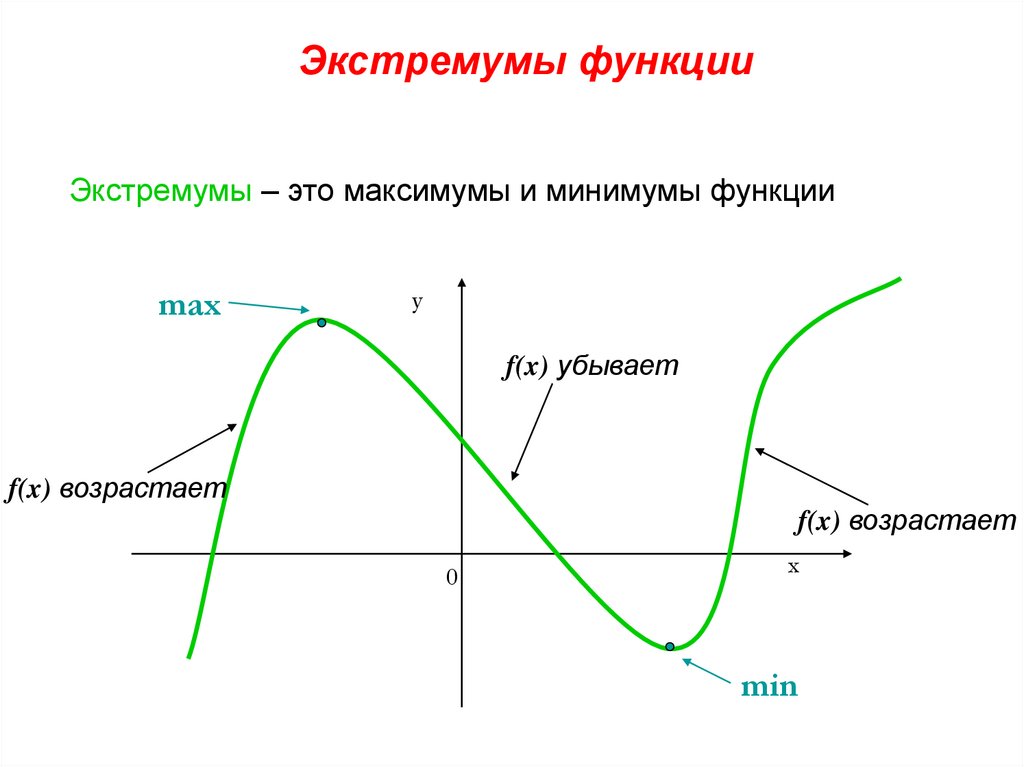
Экстремумы функции
Экстремумы – это максимумы и минимумы функции
max
y
f(x) убывает
f(x) возрастает
f(x) возрастает
0
x
min

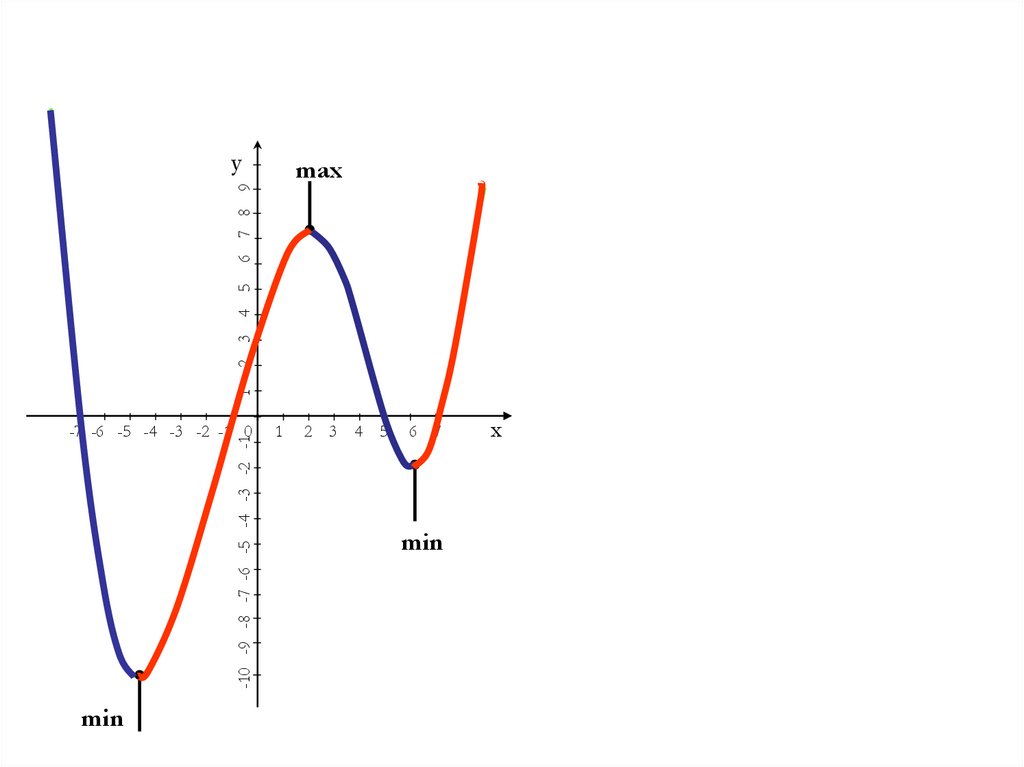
11.

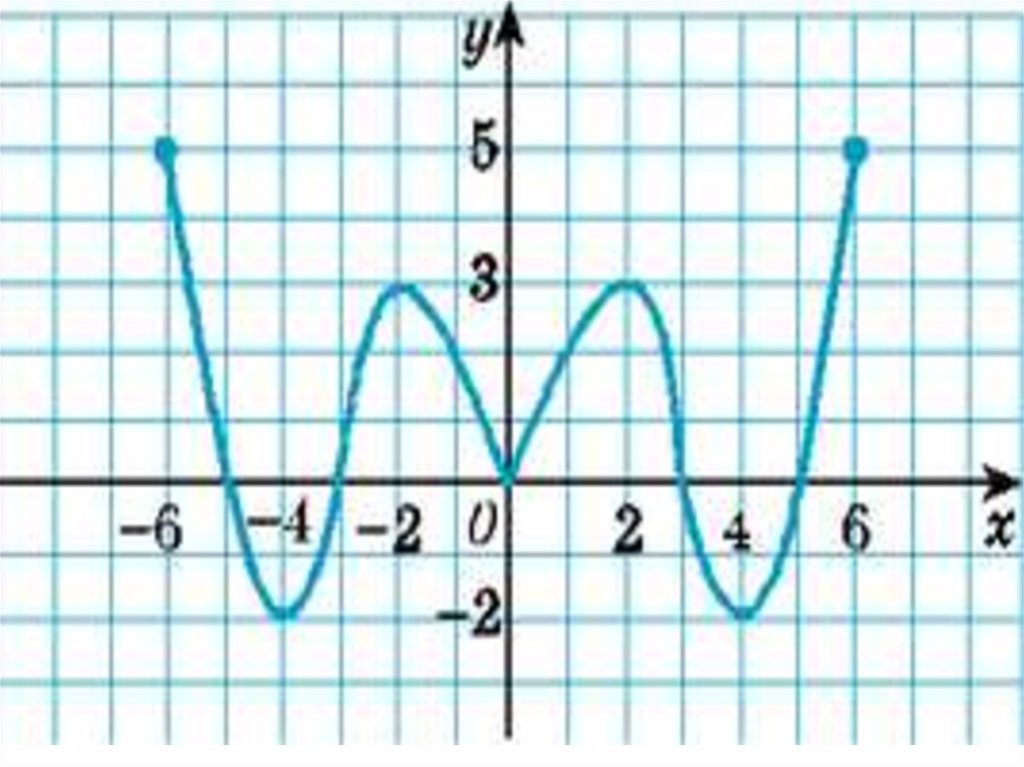
y
1
2
3
4
5
6 7 8
9
max
-10 -9 -8 -7 -6 -5 -4 -3 -2 -1
-7 -6 -5 -4 -3 -2 -1 0
min
1
2
3
4 5
6
7
min
x

12.

13. Правило для нахождения интервалов монотонности (возрастания и убывания) функции

1. Найти первую производную функции f ( x ) .
2. .Найти нули и точки разрыва f ( x ) .
3. На числовой прямой изобразить нули первой производной.
4. Определить знак f ( x ) в промежутках, на которые разбита область определения
точками из п.2
5. На интервале, где f ( x ) >0 – функция возрастает,
На интервале, где f ( x ) <0 – функция убывает

14.

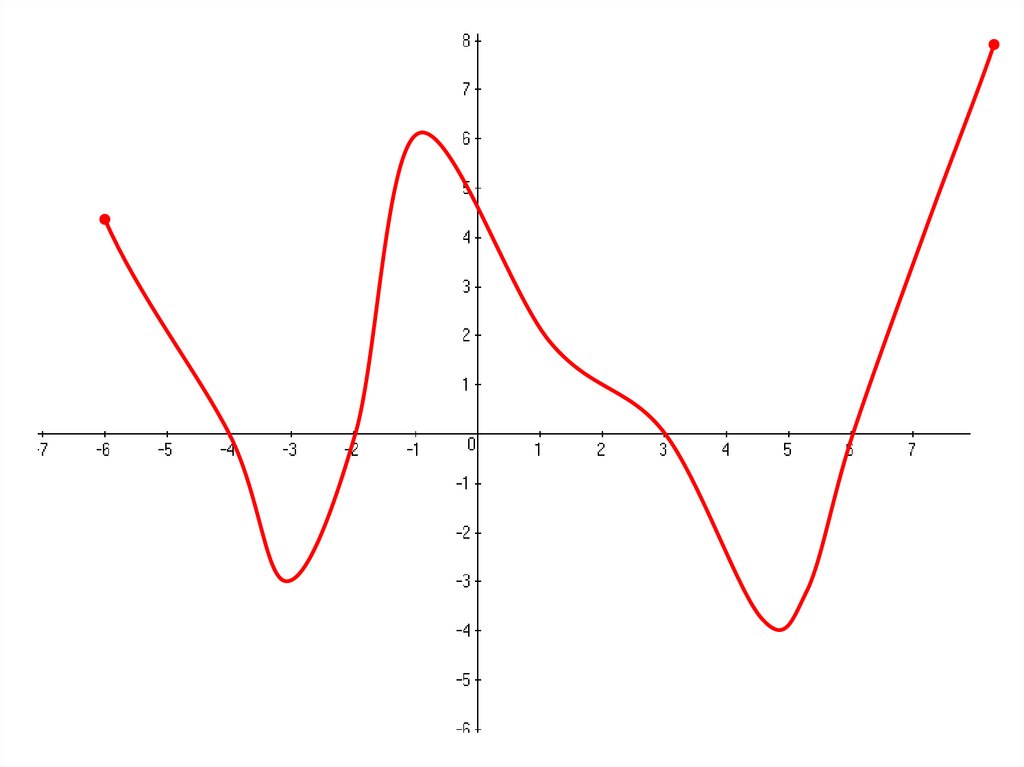
f(x) убывает при (-∞;-2)U(0;2)
f(x) возрастает при (-2;0)U(2;+∞)

15.

№1

16.

Необходимое условие экстремума:

17. Признак экстремума функции:

18. Правило для нахождения экстремумов (максимумов и минимумов) функции

Точками экстремума называются точки максимума и минимума.
1. Найти первую производную функции f ( x ) .
2. Найти нули и точки разрыва f ( x ) . Это и есть точки, подозрительные на
экстремум.
3. На числовой прямой изобразить эти точки.
4. Определить знак f ( x ) в промежутках, на которые разбита область определения
точками из п.2
5. Если при переходе через точку экстремума знак производной f ( x ) меняется с
«+» на « - », то в данной точке max.
Если при переходе через точку экстремума знак производной f ( x ) меняется с
«-» на « + », то в данной точке min.

19.

ПРИМЕР

20.

№1
№2

21.

Исследовать функцию и построить ее
график
x 4 x3
f ( x ) x2
4 3
1. Область определения – (-∞; +∞)

22.

2. Интервалы монотонности
Находим производную:
f ' ( x ) x3 x 2 2 x
Приравниваем ее к нулю:
x 3 x 2 2 x 0,
Находим критические точки:
-
x( x 2 x 2) 0,
x1=0, x2= -1, x3=2
-
+
-1
0
2
min
max
min
3. Точки экстремума:
min(-1;-0, 4), ( 2; 2,7)
max(0,0 )
+
f ( x )
x
f(x)

23.

График функции
y
0
-1
-1,4
1
x 4 x3
f ( x ) x2
4 3
2
2,8
-0,4
-1
-2,7
x

24.

Домашнее задание.
Исследовать функцию и построить
график
3
x
2
y
3x 5x
3