Похожие презентации:
Математическое программирование. Транспортная задача
1.
Математическоепрограммирование
Транспортная задача
2.
План лекции1. Основные понятия;
2. Построение математической
модели задачи;
3. Изучение методов решения
транспортной задачи.
4. Повторение пройденного
3.
Транспортная задачаТранспортная задача линейного программирования относится к
перечню классических задач, решаемых в практике деятельности
людей. Эта задача методами классической математики не решается.
Искать требуется не просто экстремум, а условный экстремум.
Методы решения задачи позволяют учитывать особенности
структуры задачи и даже отказаться от симплексного метода
решения в чистом виде.
4.
Глобальность задачи5.
История задачи• Впервые сформулирована в 1781 году Гаспаром Монжем
• Прогресс в формулировании решения был достигнут во время ВОВ
советским математиком Леонидом Канторовичем. С тех пор задача
часто встречается под названием «Транспортная задача МонжаКанторовича»
6.
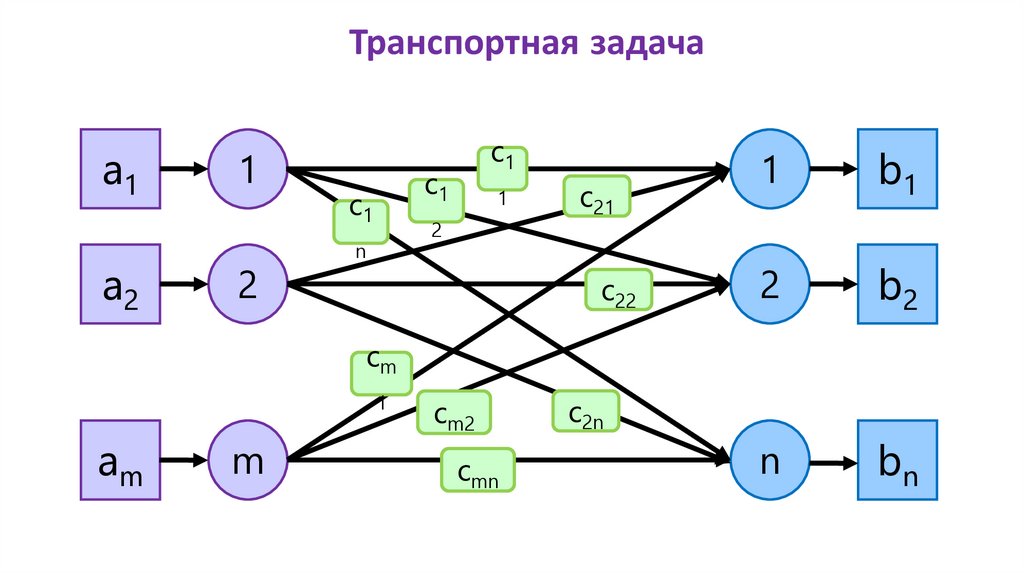
Транспортная задачаa1
a2
1
2
c1
c1
c1
1
2
n
c21
c22
1
b1
2
b2
n
bn
cm
1
am
m
cm2
cmn
c2n
7.
m – количество поставщиков продукции;n – количество потребителей продукции;
i – индекс для поставщиков;
j – индекс для потребителей;
ai , i 1, m – наличие продукции у каждого поставщика;
b j , j 1, n – потребность в продукции каждого потребителя;
cij – стоимость доставки единицы продукции от i - поставщика к j потребителю.
8.
mn
i 1
m
j 1
n
i 1
j 1
ai b j – задача называется закрытой
ai b j – задача называется открытой(с нарушенным балансом).
Решение открытой задачи сводится к решению закрытой
9.
Математическая модельxij , i 1, m, j 1, n – решение задачи
X – объемы перевозок от
поставщика к потребителю
Целевая функция
m n
Z cij xij min
– целевая функция
i 1 j 1
Ограничения
n
m
j 1
i 1
xij ai , i 1, n , xij b j , j 1, nm,
xij 0, i 1, m, j 1, n ,
m
n
ai b j
i 1
j 1
Закрытый тип задачи
10.
Методы решения• Симплекс-метод
• Итерационное улучшение плана
перевозок
• Нахождение опорного плана
• Метод северо-западного угла
(диагональный или улучшенный)
• Метод наименьшего элемента
• Итерации
11.
Симплекс метод12.
РЕШЕНИЕ ТРАНСПОРТНОЙ ЗАДАЧИЭтапы:
I. Построение начального базисного
решения : метод северо-западного угла,
метод наименьшей стоимости
(минимального элемента), метод Фогеля
II. Итеративный процесс поиска
оптимального решения (метод
потенциалов).
13.
I.Метод наименьшей стоимости.
Пусть m 3 поставщиков продукции,
n 4 потребителей продукции
Запасы A (15,25,10) ,
Потребность B (5,15,15,15)
10 2 20 11
7 9 20
Затраты на перевозку продукции C (cij ) 12
4 14 16 18
1
2
3
Потребность
1
2
3
4
10
12
4
5
2
7
14
15
20
9
16
15
11
20
18
15
Запасы
15
25
10
50
14.
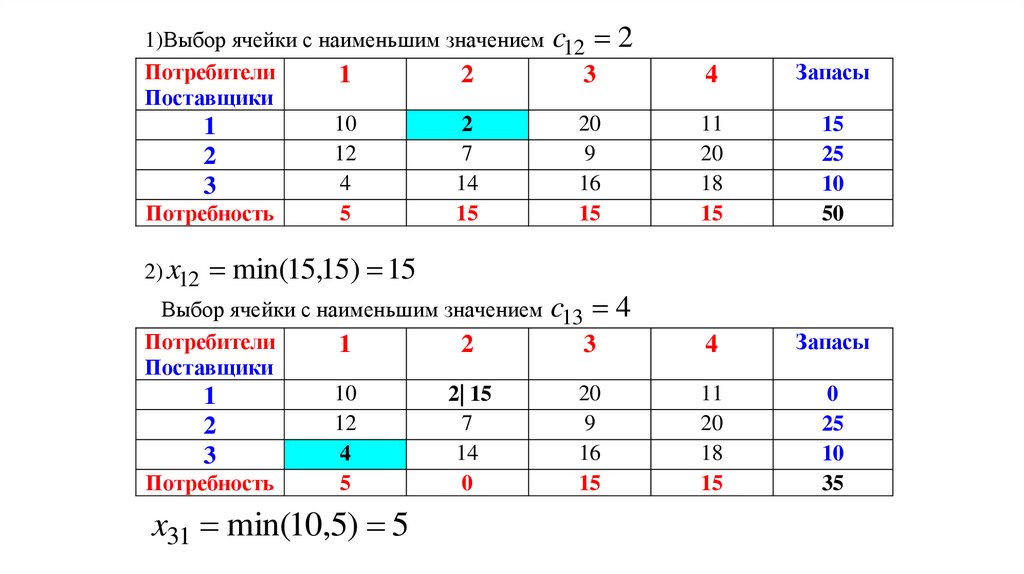
1)Выбор ячейки с наименьшим значением c12 2Потребители
1
2
3
Поставщики
10
20
2
1
12
7
9
2
4
14
16
3
Потребность
5
15
15
4
Запасы
11
20
18
15
15
25
10
50
4
Запасы
11
20
18
15
0
25
10
35
2) x12 min(15,15) 15
Выбор ячейки с наименьшим значением c13 4
Потребители
1
2
3
Поставщики
10
20
2| 15
1
12
7
9
2
14
16
4
3
Потребность
5
0
15
x31 min(10,5) 5
15.
3) Выбор ячейки с наименьшим значением c23 9Потребители
Поставщики
1
2
3
4
Запасы
1
2
3
10
12
4|5
0
2| 15
7
14
0
20
9
16
15
11
20
18
15
0
25
5
30
4
Запасы
11
20
18
15
0
10
5
15
Потребность
4) x2,3 min( 25,15) 15
Выбор ячейки с наименьшим значением c34 18
Потребители
1
2
3
Поставщики
10
20
2| 15
1
12
7
9 | 15
2
14
16
4 |5
3
Потребность
0
0
0
5) x3, 4 min(5,15) 5
16.
Выбор ячейки с наименьшим значением c24 20Потребители
1
2
3
Поставщики
10
20
2| 15
1
12
7
9 | 15
2
14
16
4 |5
3
Потребность
0
0
0
4
Запасы
11
20
18 | 5
10
0
10
0
10
6) x2, 4 min(10,10) 10
Должно быть базовых m n 1 3 4 1 6 переменных
Есть только 5, поэтому выбираем любую x1, 4 0
Потребители
Поставщики
1
2
3
4
Запасы
1
2
3
10
12
4 |5
0
2| 15
7
14
0
20
9 | 15
16
0
11 | 0
20 | 10
18 | 5
0
0
0
0
0
Потребность
17.
Первое допустимое решениеx12 15 , x1,4 0 , x2,3 15 , x2, 4 10 , x31 5 , x3, 4 5
Значение функции цели
Z 15 2 0 11 15 9 10 20 5 4 5 18 475
30
135
200
20
90
18.
II. Метод потенциаловВ методе потенциалов каждой строке i и каждому столбцу j транспортной
таблицы ставятся в соответствие числа (потенциалы) ui (поставщики) и vj
(потребители). Для каждой базисной переменной xij потенциалы ui и vj
удовлетворяют уравнению
ui + vj = сij
Потребители
Поставщики
1
2
3
4
Запасы
1
2
3
10
12
4 |5
5
2| 15
7
14
15
20
9 | 15
16
15
11 | 0
20 | 10
18 | 5
15
15
25
10
50
Потребность
Потенциалы: ui , i 1,3 ,
v j , j 1,4 .
19.
Определяем потенциалы для всех базисных переменныхu1 v2 2
u1 v4 11
u2 v3 9
u2 v4 20
u3 v1` 4
u3 v4` 18
Уравнений 6 неизвестных 7:
Присваиваем одному из них произвольное значение (обычно u1 0 )
u1 0 v2 2, v4 11 ,
v4 11 u2 9, u3 7 ,
u3 7 v1 3,
u2 9 v3 0
u1 0 , u2 9 , u3 7
v1 3, v2 2 , v3 0 , v4 11
20.
ПотребителиПоставщики
1
2
3
4
Запасы
1
2
3
10
12
4 |5
5
2| 15
7
14
15
20
9 | 15
16
15
11 | 0
20 | 10
18 | 5
15
15
25
10
50
Потребность
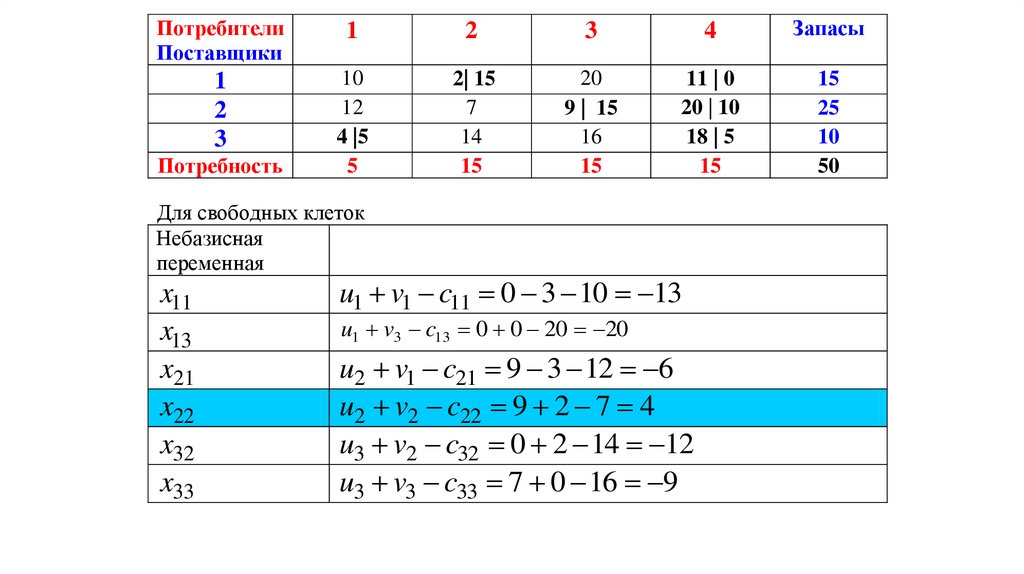
Для свободных клеток
Небазисная
переменная
x11
x13
x21
x22
x32
x33
u1 v1 c11 0 3 10 13
u1 v3 c13 0 0 20 20
u2 v1 c21 9 3 12 6
u2 v2 c22 9 2 7 4
u3 v2 c32 0 2 14 12
u3 v3 c33 7 0 16 9
21.
ПотребителиПоставщики
1
2
3
4
Запасы
1
2
3
10
12
4 |5
5
2| 15 –
7 +
14
15
20
9 | 15
16
15
+ 11 | 0
20 | 10
18 | 5
15
15
25
10
50
Потребность
–
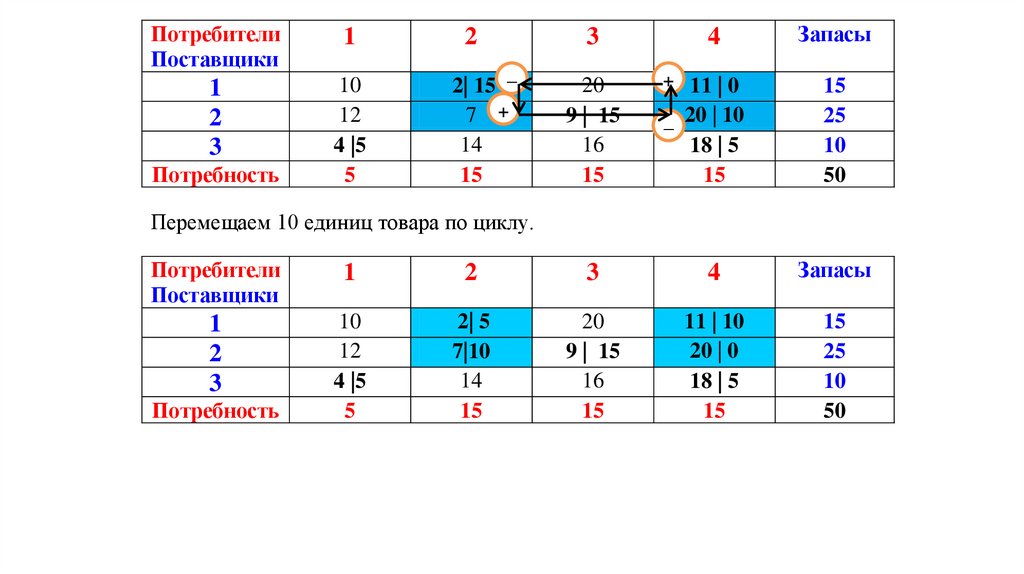
Перемещаем 10 единиц товара по циклу.
Потребители
Поставщики
1
2
3
4
Запасы
1
2
3
10
12
4 |5
5
2| 5
7|10
14
15
20
9 | 15
16
15
11 | 10
20 | 0
18 | 5
15
15
25
10
50
Потребность
22.
Допустимое решениеx12 5 , x1, 4 10 , x2, 2 10 , x2,3 5 , x31 5 , x3, 4 5
Значение функции цели
Z 5 2 10 11 10 7 15 9 5 4 5 18 435
10
110
475 435 40
70
135
20
90
23.
ПотребителиПоставщики
1
2
3
4
Запасы
10
20
2| 5
11 | 10
15
12
20 | 0
7|10
9 | 15
25
14
16
4 |5
18 | 5
10
Потребность
5
15
15
15
50
Определяем потенциалы для всех базисных переменных ((2,4) уже не
базисная)
1
2
3
u1 v2 2
u1 v4 11
u2 v2 7
u2 v3 9
u3 v1` 4
u3 v4` 18
Уравнений 6 неизвестных 7:
u1 0 v2 2, v4 11 ,
v2 2 u2 5 ,
u2 5 v3 4,
v4 11 u3 7
u3 7 v1 3
24.
ПотребителиПоставщики
1
2
3
4
Запасы
1
2
3
10
12
4 |5
5
2| 5
7|10
14
15
20
9 | 15
16
15
11 | 10
20
18 | 5
15
15
25
10
50
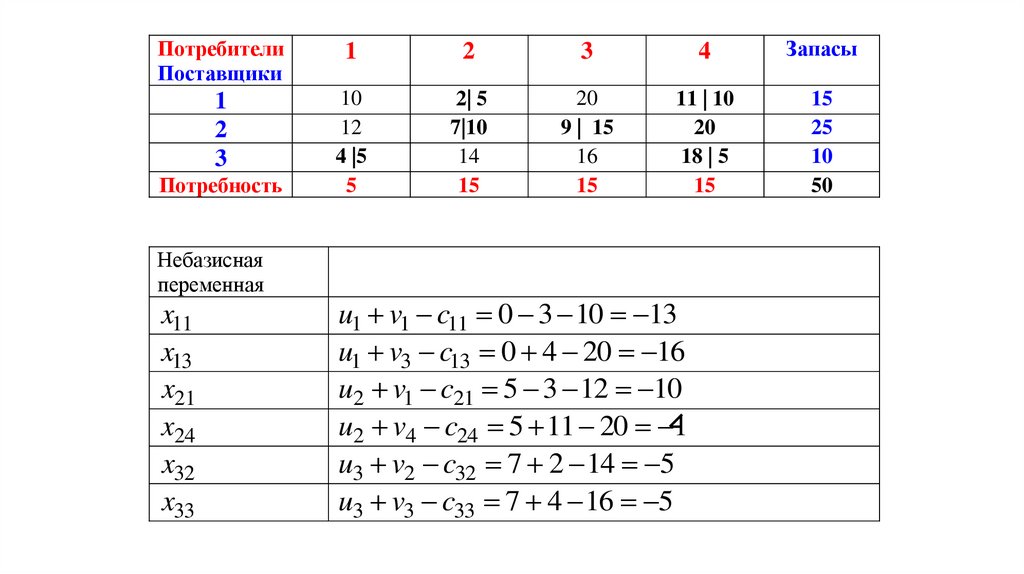
Потребность
Небазисная
переменная
x11
x13
x21
x24
x32
x33
u1 v1 c11 0 3 10 13
u1 v3 c13 0 4 20 16
u2 v1 c21 5 3 12 10
u2 v4 c24 5 11 20 1
u3 v2 c32 7 2 14 5
u3 v3 c33 7 4 16 5
25.
Решение задачи о расстановкескобок при перемножении матриц
Вычислим количество операций умножения, которые необходимо
выполнить при перемножении трех матриц A1 , A2 и A3 размерностью
соответственно 10 100, 100 5 и 5 50.
Заметим, что операция умножения матриц ассоциативна и
следовательно, A1 A2 A3 ( A1 A2 ) A3 A1 ( A2 A3 ).
Несложно подсчитать, что количество операций умножения, которые
необходимо выполнить при вычислении произведения ( A1 A2 ) A3
будет 10 100 5 10 5 50 7500, а при вычислении A1 ( A2 A3 ) –
100 5 50 10 100 50 75000, т.е. в 10 раз больше.
26.
Рекуррентноесоотношение,
позволяющее
минимальное количество операций умножения:
вычислить
0, i j,
mi , j pi 1 pi pi 1 , j i 1,
min (m m
p
p
p
),
j
1
1
.
i
,
k
k
1
,
j
i
1
k
j
i k j
27.
Определим минимальное количество операций умножения дляматриц A1, A2, и A3, из рассмотренного выше примера:
m1,3 min (m1,k mk 1,3 p0 pk p3 );
1 k 3
k 1, m1,1 m2,3 p0 p1 p3 0 p1 p2 p3 p0 p1 p3
0 100 5 50 10 100 50 75 000;
k 2, m1, 2 m3,3 p0 p2 p3 p0 p1 p2 0 p0 p2 p3
10 100 5 0 10 5 50 7500;
m1,3 min( 75 000, 7500 ) 7500 .
28.
ФункцияOptimalM,
реализующая
алгоритм
поиска
оптимальной расстановки скобок при перемножении нескольких
матриц.
Функция OptimalM является рекурсивной, так как она в
процессе своей работы вызывает саму себя. Дно рекурсии
достигается при совпадении значений двух первых параметров
функции.
//- MultiMatrix.h
#define OPTIMALM_PARM(x) ((int*)x) // представлениe двумерного массива
int OptimalM(
int i,
// [in] номер первой матрицы
int j,
// [in] номер последней матрицы
int n,
// [in] количество матриц
const int c[], // [in] массив размерностей
int* s
// [out] результат: позиции скобок
);
29.
// - MultiMatrix.cpp#include "stdafx.h"
#include <memory.h>
#include "MultiMatrix.h"
#define INFINITY 0x7fffffff
int OptimalM(int i, int j, int n, const int c[], int *s)
{
#define OPTIMALM_S(x1,x2) (s[(x1-1)*n+x2-1])
int o =INFINITY, bo = INFINITY;
if (i < j)
{
for (int k = i; k < j;k++)
{
bo = OptimalM(i,k, n, c, s)+
OptimalM(k+1,j,n, c, s)+ c[i- 1]*c[k]*c[ j];
if (bo < o){o = bo; OPTIMALM_S(i,j) = k;}
}
}
else o = 0;
return o;
#undef OPTIMALM_S
};
30.
// --- main расстановка скобок#include "stdafx.h"
#include <cmath>
#include <memory.h>
#include <iostream>
#include "MultiMatrix.h"
#define N 6
int _tmain(int argc, _TCHAR* argv[])
{
int Mc[N+1] = {30,35,15,5,10,20,25}, Ms[N][N], r = 0, rd = 0;
memset(Ms,0,sizeof(int)*N*N);
r = OptimalM(1, N, N, Mc, OPTIMALM_PARM(Ms));
setlocale(LC_ALL, "rus");
std::cout<<std::endl;
std::cout<<std::endl<< "- расстановка скобок (рекурсивное решение) "
<< std::endl;
std::cout<<std::endl<< "размерности матриц: ";
for (int i = 1; i <= N; i++) std::cout<<"("<<Mc[i-1]<<","<<Mc[i]<<") ";
std::cout<<std::endl<< "минимальное количество операций умножения: " << r;
std::cout<<std::endl<<std::endl<<"матрица S"<<std::endl;
for (int i = 0; i < N; i++)
{
std::cout<<std::endl;
for (int j = 0; j < N; j++) std::cout<<Ms[i][ j]<< " " ;
}
std::cout<<std::endl;
system("pause");
return 0; };
31.
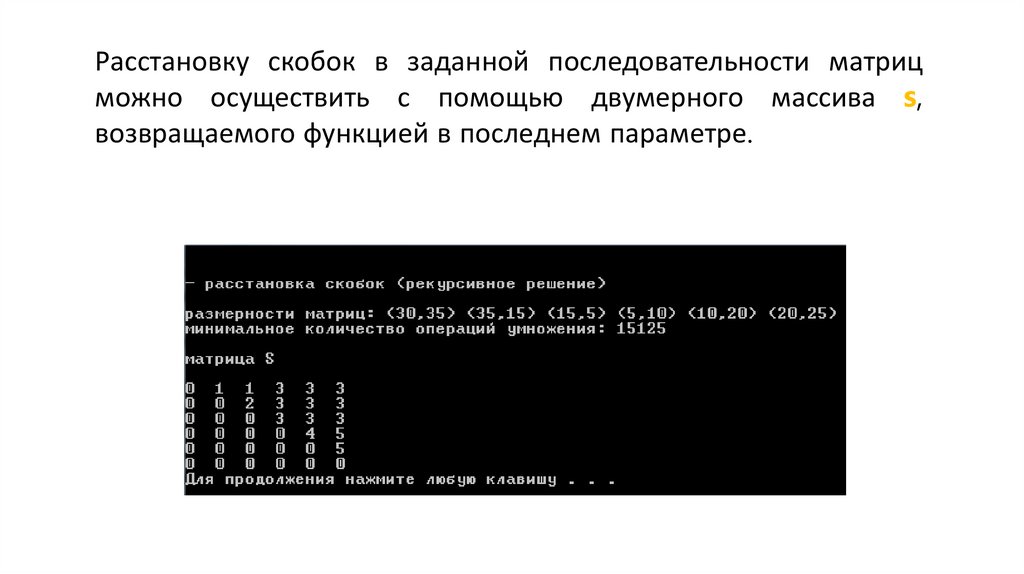
Расстановку скобок в заданной последовательности матрицможно осуществить с помощью двумерного массива s,
возвращаемого функцией в последнем параметре.
32.
Скобки расставляются по принципу «сначала внешние – затемвнутренние». Найдем элемент (1, 6) в матрице s. Он равен 3. Это означает,
что точка разрыва находится между первой и шестой матрицей после
третьей матрицы, что позволяет расставить внешние скобки следующим
образом: ( A1 A2 A3 ) ( A4 A5 A6 ).
Точку разрыва между первой и третьей матрицей определяет элемент
(1, 3), а между четвертой и шестой – (4, 6). После расстановки скобок
выражение
будет
выглядеть
следующим
образом
( A1 ( A2 A3 )) (( A4 A5 ) A6 ). Полученная расстановка скобок позволяет
получить минимальное количество операций умножения, равное 15 125.

























 Математика
Математика Программирование
Программирование








