Задача о максимальном потоке

1.

Кичмаренко О.Д.
Задача о максимальном
потоке
1

2.

Сетевые модели.
6. Задача о максимальном потоке.
У некоторой компании «Аврора» в Измаиле есть
фабрика (источник s), производящая стулья, а в
Одессе - склад (сток t), где эти стулья хранятся.
Компания арендует место на грузовиках других
фирм для доставки стульев с фабрики на склад.
Поскольку грузовики ездят по определенным
маршрутам (ребрам) между городами
(вершинами) и имеют ограниченную
грузоподъемность, компания может перевозить
не более c(u , v) ящиков в день между каждой
парой городов u и v.
Компания не может повлиять на маршруты и
пропускную способность, то есть она не может
менять транспортную сеть.
Ее задача определить, какое наибольшее
количество p ящиков в день можно отгружать, а
затем производить именно такое количество,
поскольку не имеет смысла производить больше
стульев, чем можно отправить на склад.
2

3.

Сетевые модели.
6. Задача о максимальном потоке.
3

4.

Сетевые модели.
6. Задача о максимальном потоке.
4

5.

Сетевые модели.
6. Задача о максимальном потоке.
Метод Форда-Фалкерсона
Метод Форда-Фалкерсона
Это именно метод, а не алгоритм, поскольку он допускает несколько
реализаций с различным временем выполнения.
Метод Форда-Фалкерсона базируется на трех важных концепциях.
Это — остаточные сети, увеличивающие пути и разрезы.
Метод Форда-Фалкерсона является итеративным.
Вначале величине потока присваивается значение ноль:
f (u,v) = 0 ∀ u,v ∈ V
На каждой итерации величина потока увеличивается посредством
поиска «увеличивающего пути» (т.е. некоторого пути от источника s к
стоку t, вдоль которого можно послать больший поток) и последующего
увеличения потока.
Этот процесс повторяется до тех пор, пока уже невозможно отыскать
увеличивающий путь.
5

6.

Сетевые модели.
6. Задача о максимальном потоке.
Метод Форда-Фалкерсона
6

7.

Сетевые модели.
6. Задача о максимальном потоке.
Метод Форда-Фалкерсона
7

8.

Сетевые модели.
6. Задача о максимальном потоке.
Метод Форда-Фалкерсона
Разрезы транспортных сетей
Разрезом (cut) (S,T) транспортной сети G=(V,E) называется
разбиение множества вершин на множества S и T=V-S
такие, что s∈S, а t∈T.
Если f — поток, то чистый поток через разрез (S,T) обозначим
как f(S,T).
Пропускную способность разреза (S,T) обозначим,
соответственно, c(S,T).
8

9.

Сетевые модели.
6. Задача о максимальном потоке. Идея алгоритма.
Идея алгоритма нахождения максимального потока состоит в
нахождении сквозных путей с положительными потоками от
источника к стоку.
Нахождение очередного сквозного пути предполагает
задействование части пропусной спосообности ребер. Поэтому
следующий сквозной путь ищется на остаточной сети.
Максимальный поток вычисляется как сумма потоков в сквозных
путях.
Более общей является задача с нижними положительными
границами пропускных способностей.
При этом сеть может вообще не иметь допустимого потока.
В этом случае интерес представляет нахождение как
максимального, так и минимального потоков в сети.
9

10.

Сетевые модели.
6. Задача о максимальном потоке.
Базовый алгоритм Форда-Фалкерсона
10

11.

Сетевые модели.
6. Задача о максимальном потоке.
Базовый алгоритм Форда-Фалкерсона
11

12.

Сетевые модели.
6. Задача о максимальном потоке.
Базовый алгоритм Форда-Фалкерсона. ПРИМЕР
12

13.

Сетевые модели.
6. Задача о максимальном потоке.
Базовый алгоритм Форда-Фалкерсона. ПРИМЕР
13

14.

Сетевые модели.
6. Задача о максимальном потоке.
Базовый алгоритм Форда-Фалкерсона. ПРИМЕР
14

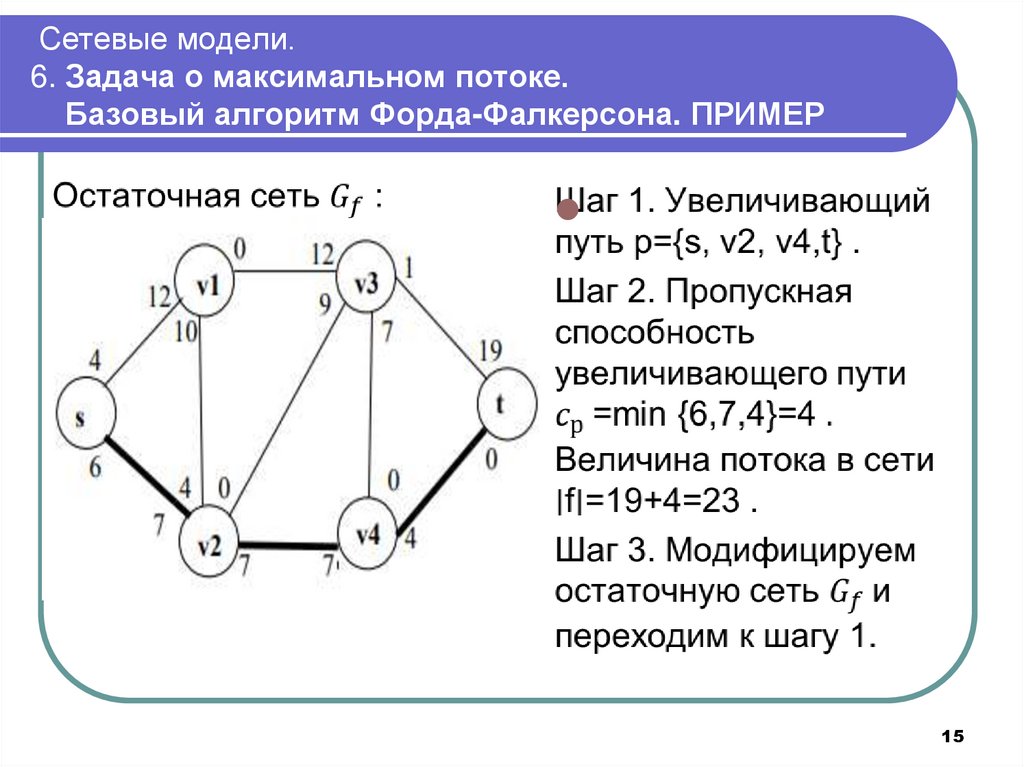
15.

Сетевые модели.
6. Задача о максимальном потоке.
Базовый алгоритм Форда-Фалкерсона. ПРИМЕР
15

16.

Сетевые модели.
6. Задача о максимальном потоке.
Базовый алгоритм Форда-Фалкерсона. ПРИМЕР
Шаг 1. Увеличивающий
путь построить нельзя.
Переходим к шагу 4.
Шаг 4. Максимальный
поток в сети ∣f∣=23 .
Вычисляем потоки по
ребрам, которые
обеспечивают
максимальный поток в
сети.
16

17.

Сетевые модели.
6. Задача о максимальном потоке.
Базовый алгоритм Форда-Фалкерсона. ПРИМЕР
Расчет пропускных мощностей отдельных ребер
Находим ребра, в которых изменились мощности
потоков.
На них находим мощности, которые уменьшились
– они указывают на направление потока по
ребру.
Мощность потока на этом ребре равна разности
между начальной и конечной мощностями.
17

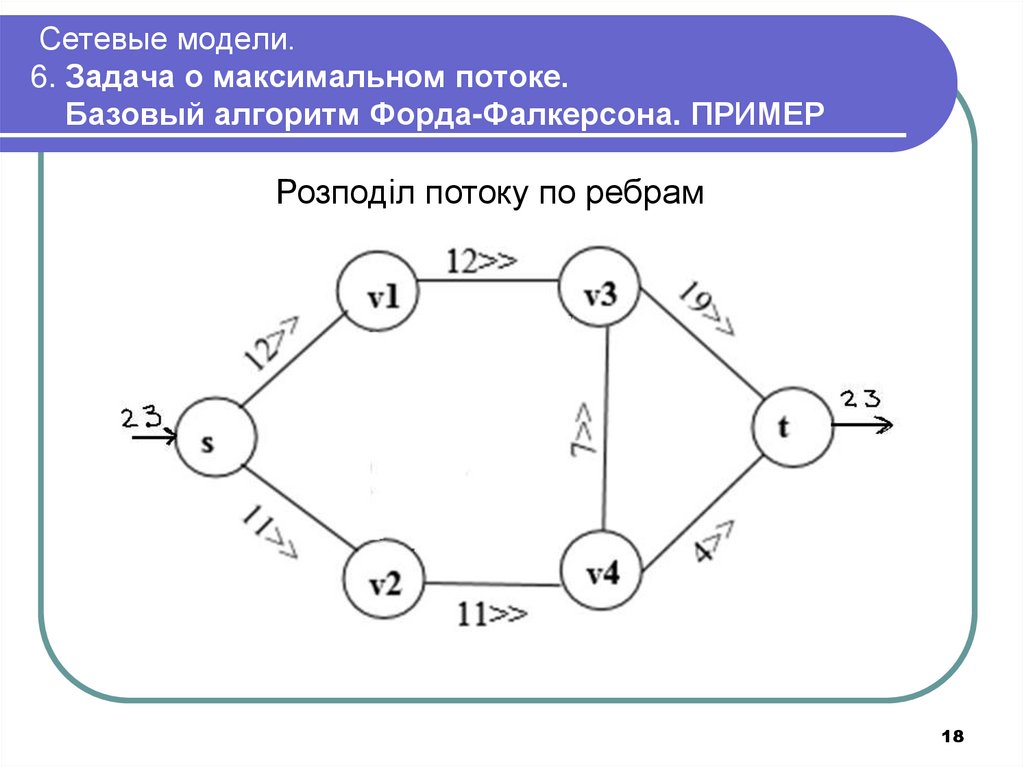
18.

Сетевые модели.
6. Задача о максимальном потоке.
Базовый алгоритм Форда-Фалкерсона. ПРИМЕР
Розподіл потоку по ребрам
18

19.

Сетевые модели.
6. Задача о максимальном потоке.
ІНДИВІДУАЛЬНЕ
З А В Д А Н Н Я.
Нафто-газова компанія володіє
мережею газопроводів, через які газ
перекачується від місця видобутку до
газосховищ. Частина цієї мережі
представлена на малюнку
(пропускна потужність газопроводів
показана
в тис. куб.м/год.).
Знайдіть максимальний потік в
мережі між парами вузлів, що
вказані у варіанті на наступних
Значення j = друга цифра числа,
слайдах (початковий та кінцевий). отриманого після складання цифр дати
Який максимальний потік може
вашого народження
забезпечити лінія 1-4?
(22.04.1988 2+2+0+4+1+9+8+8=34,
Скільки часу займе перекачка 100
значить j=4).
На малюнку 2j 3j 4j читаєте як двозначне
тис. куб. м газу через мережу?
число з останньою цифрою j
19

20.

Сетевые модели.
6. Задача о максимальном потоке.
ІНДИВІДУАЛЬНЕ
З А В Д А Н Н Я.
Звіт містить:
1. Умову задачі в вигляді графа з вказаними початковим та кінцевим вузлами, а
також пропускними потужностями по кожному ребру мережі.
2. Розв’язок за базовим алгоритмом методу Форда-Фалкерсона з розписаними
ітераціями.
Відповідь з указанням максимальної пропускної потужності всієї мережі,
граф з указанням розподілу потоків по ребрам мережі,
а також відповіді всі питання задачі.
20

21.

Сетевые модели.
6. Задача о максимальном потоке.
ІНДИВІДУАЛЬНЕ
ВАРІАНТИ
початок
кінець
1
3
Жданов Артем
1
6
Кійко Богдан
1
Костанда Даніїл
З А В Д А Н Н Я.
ЗАВДАНЬ
початок
кінец
ь
початок
кінец
ь
2
5
5
3
Буравльова Катерина
2
6
Бабчинський Олександр
5
2
7
Власіхін Іван
2
7
Бордюжевич Олексій
3
2
5
Гичак Данило
3
1
Волков Данило
Миронов Олексій
2
6
Головань Ігор
3
5
Михайлюченко Даніїл
2
7
Григор’єва Анна
3
Мо Асунсау Іванна
3
1
Ковальов Данило
Поздняков Дмитро
3
5
Лубневський Сергій
3
6
Семчук Владислав
5
2
Франчук Богдан
5
3
5
7
КНП-211
Дверницька Олександра
Рибак Дмитро
Шеленгівський Андрій
початок
кінец
ь
7
5
Архіпова Аліса
7
2
6
Врублевська Юлія
7
1
5
7
Голубов Владислав
6
3
Карлінський Владислав
6
1
Дубська Олена
6
2
6
Кукурудза Дар’я
6
2
Коваленко Ярослав
6
1
5
2
Лічкун Микита
6
3
Михайлюк Мирослава
5
7
5
3
Моторіна Ніколь
7
1
Ніколайчук Анастасія
5
3
5
7
Попович Сергій
2
6
5
2
Попов Петро
6
1
Сова Станіслав
2
5
Тимофєєв Євгеній
3
6
Шарпіло Дмитро
6
2
Солтановський Борис
2
7
Хіміч Анастасія
3
5
Червоний Данило
3
1
Цапкалов-Старченко
Григорій
3
1
Щербаков Дмитро
2
7
КНП-212
Білал Наіма
Мохсені Софіані Микита
КНП-213
Ілечко Сергій
КНД-211
Азімова Олександра
Панченко Валерія
21