Похожие презентации:
Угол между прямой и плоскостью
1.
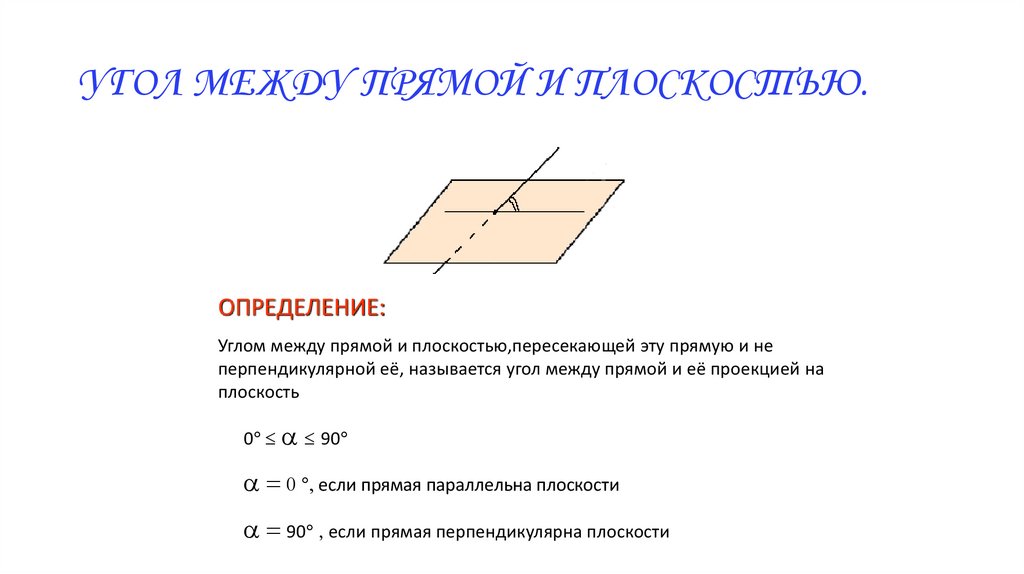
УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ.ОПРЕДЕЛЕНИЕ:
Углом между прямой и плоскостью,пересекающей эту прямую и не
перпендикулярной её, называется угол между прямой и её проекцией на
плоскость
0 a 90
a = 0 , если прямая параллельна плоскости
a = 90 , если прямая перпендикулярна плоскости
2.
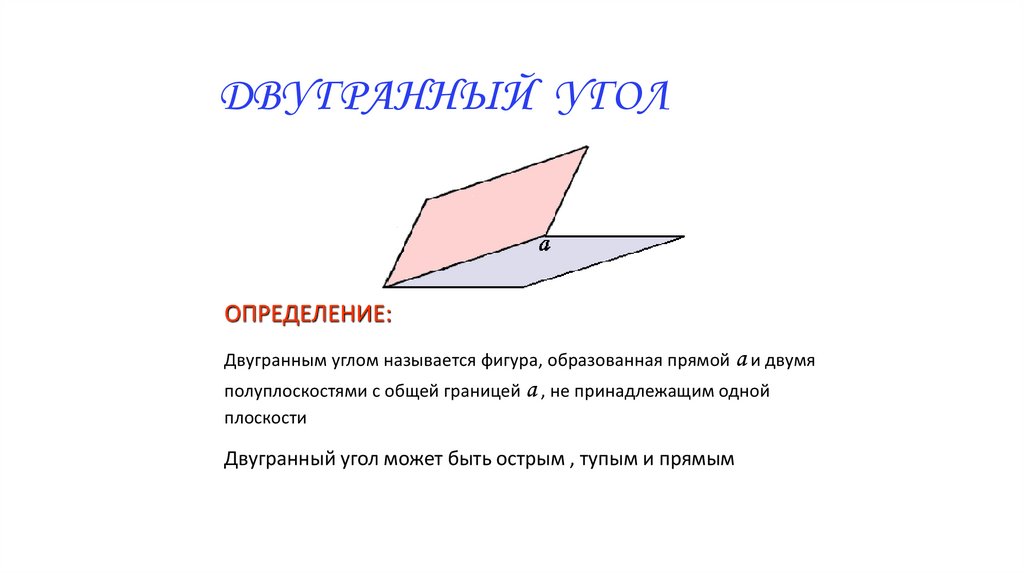
ДВУГРАННЫЙ УГОЛОПРЕДЕЛЕНИЕ:
Двугранным углом называется фигура, образованная прямой а и двумя
полуплоскостями с общей границей а , не принадлежащим одной
плоскости
Двугранный угол может быть острым , тупым и прямым
3.
Линейный уголОПРЕДЕЛЕНИЕ:
Линейный угол -- угол, стороны которого являются лучами,
перпендикулярными к ребру двугранного угла, а вершина лежит на его
ребре
Градусной мерой двугранного угла называется градусная мера его
линейного угла.
Все линейные углы двугранного угла равны
4.
УпражнениеВ кубе A…D1 найдите угол между
плоскостями ABC и CDD1.
Ответ: 90o.
5.
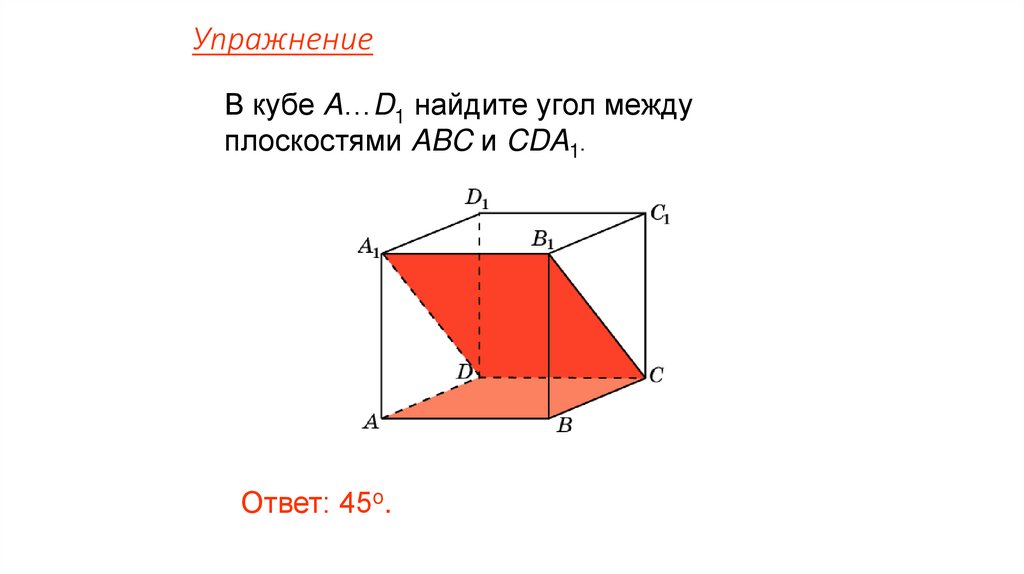
УпражнениеВ кубе A…D1 найдите угол между
плоскостями ABC и CDA1.
Ответ: 45o.
6.
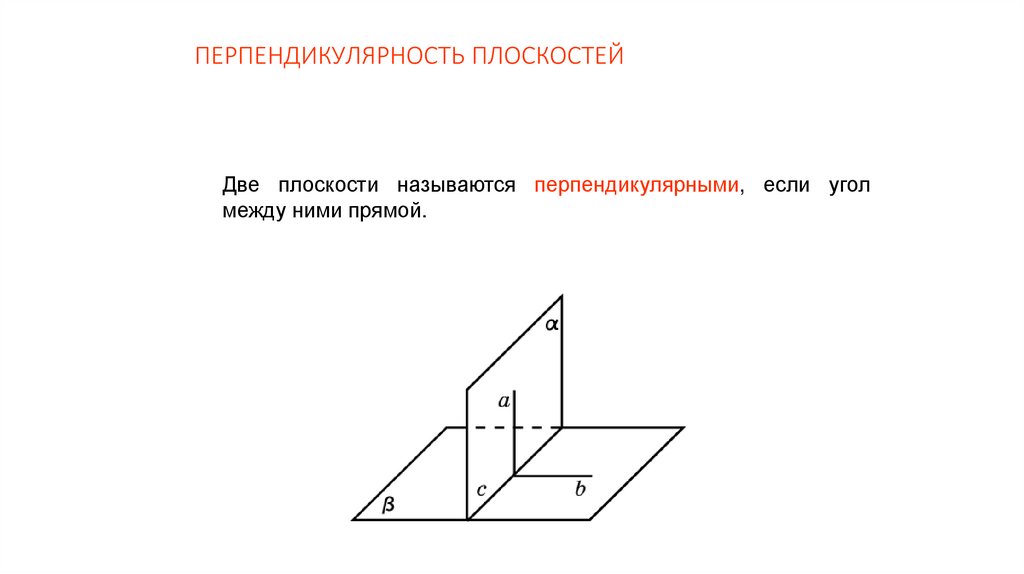
ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙДве плоскости называются перпендикулярными, если угол
между ними прямой.
7.
ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПЛОСКОСТЕЙ :
Если одна из двух плоскостей проходит через прямую,
перпендикулярную к другой плоскости, то такие
плоскости перпендикулярны
8.
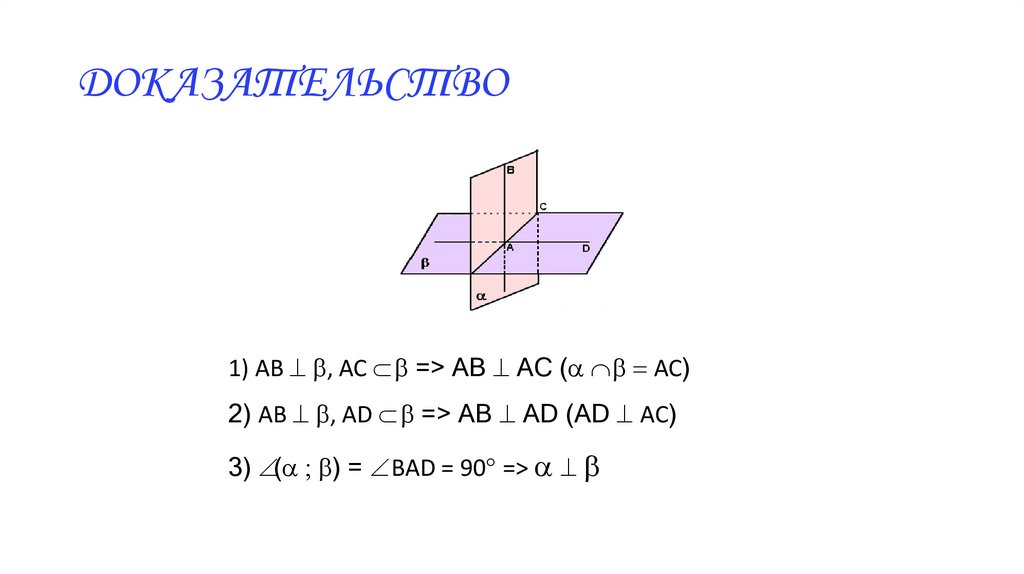
ДОКАЗАТЕЛЬСТВО1) АВ ^ b, АС b => АВ ^ АС (a b = АС)
2) АВ ^ b, АD b => АВ ^ АD (АD ^ AC)
3) (a ; b) = BAD = 90 => a ^ b
9.
ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙСЛЕДСТВИЕ ИЗ ПРИЗНАКА ПЕРПЕНДИКУЛЯРНОСТИ ПЛОСКОСТЕЙ:
Плоскость, перпендикулярная к прямой, по которой
пересекаются две данные плоскости, перпендикулярна
к каждой из этих плоскостей
10.
ОпределениеПерпендикуляром, проведённым из точки А
к плоскости α, называется отрезок АН. Точка Н
называется основанием этого перпендикуляра
A
H
α
A⏊α
AH — перпендикуляр
H — основание
перпендикуляра
11.
AM
H
α
12.
AM
H
α
13.
AM
H
α
14.
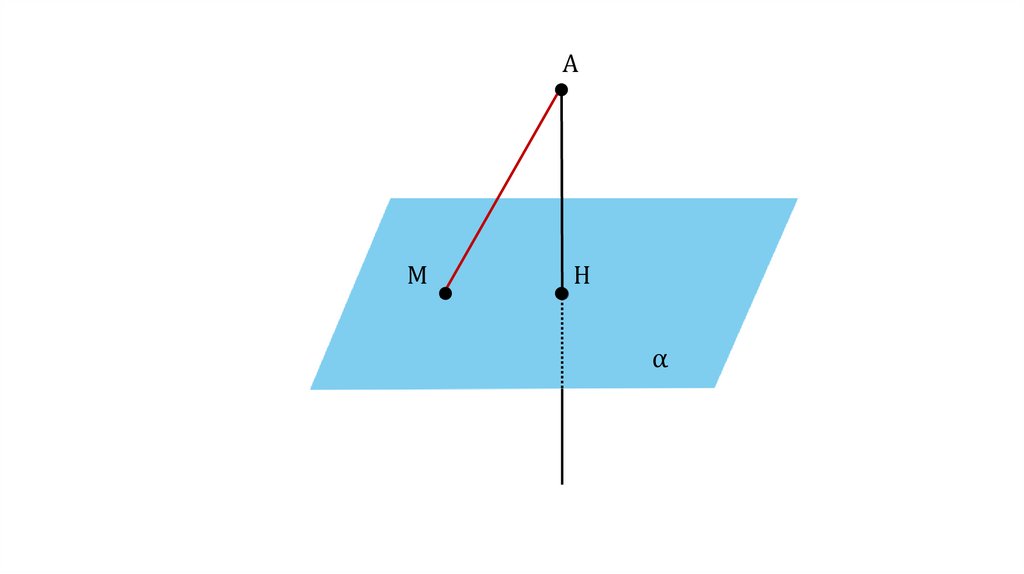
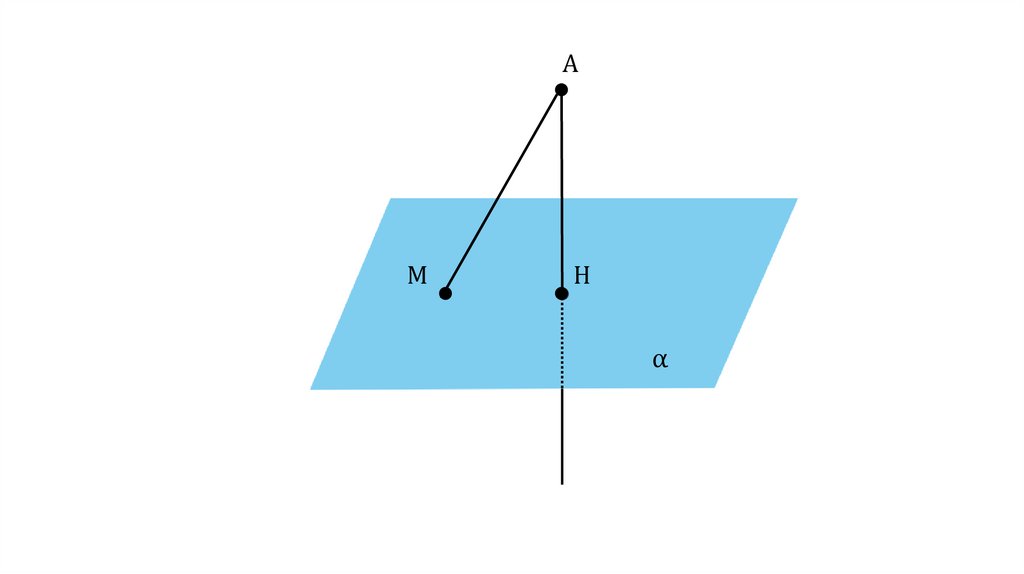
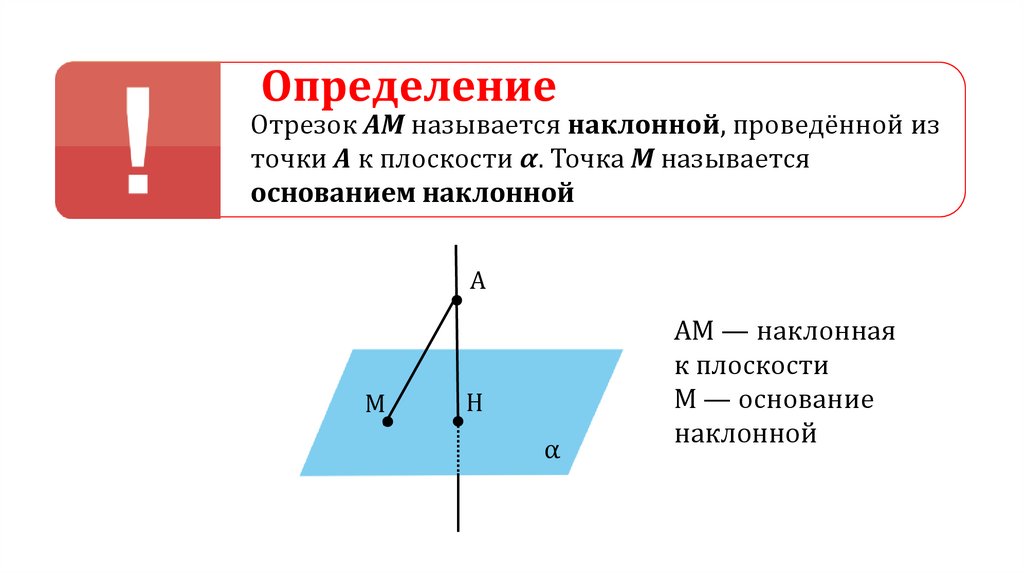
ОпределениеОтрезок АМ называется наклонной, проведённой из
точки А к плоскости α. Точка М называется
основанием наклонной
A
M
H
α
AM — наклонная
к плоскости
M — основание
наклонной
15.
AM
H
α
16.
AM
H
α
17.
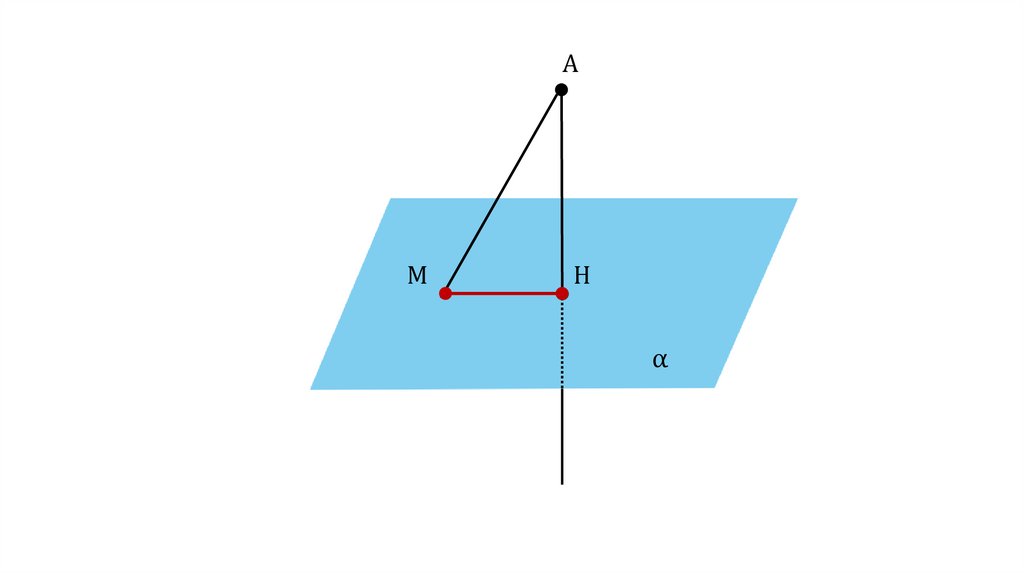
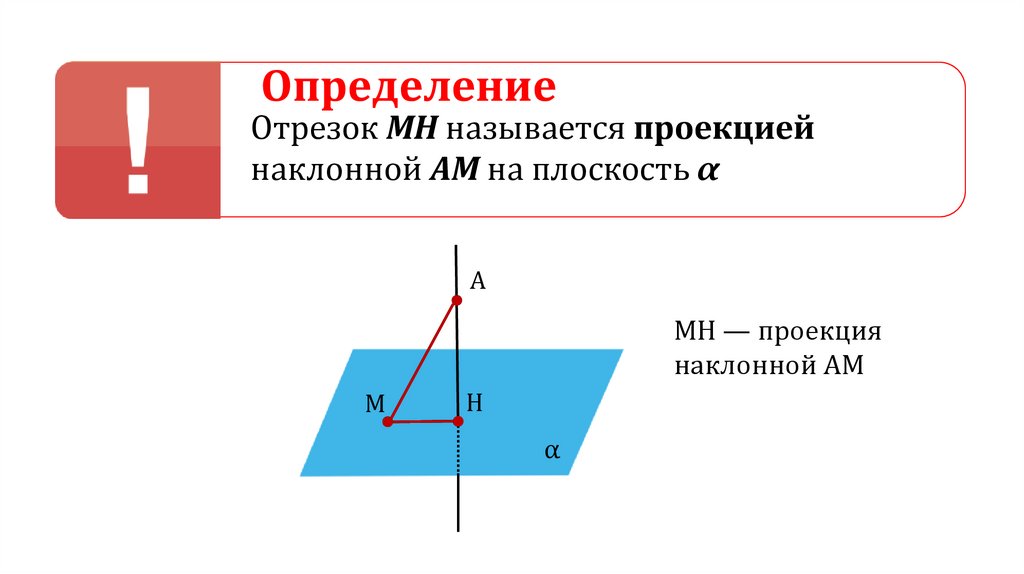
ОпределениеОтрезок МН называется проекцией
наклонной АМ на плоскость α
A
MH — проекция
наклонной AM
M
H
α
18.
AM
H
α
19.
AM
H
α
AH <? AM
20.
AM
H
α
21.
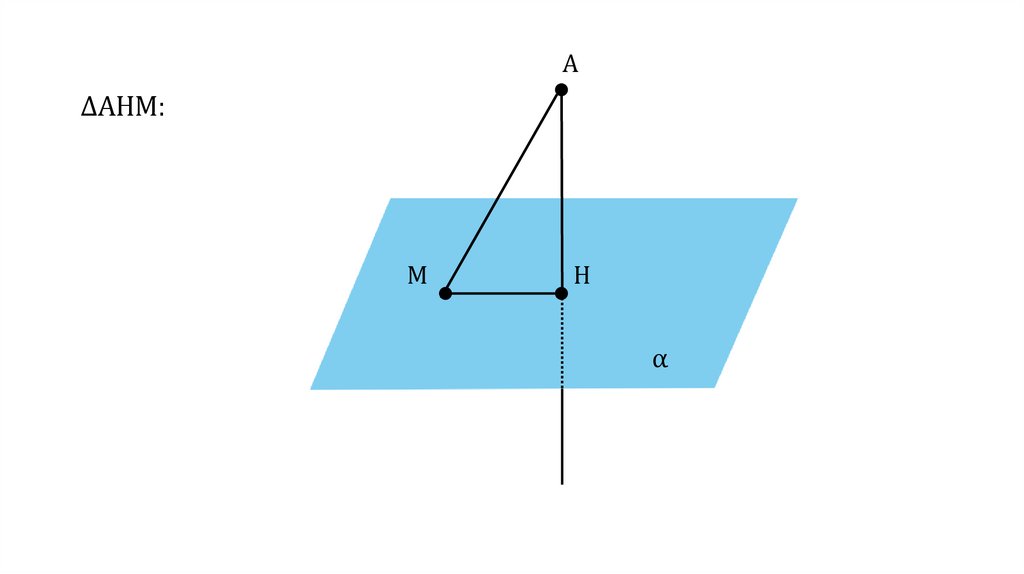
A∆AHM:
M
H
α
22.
A∆AHM:
M
H
α
23.
A∆AHM:
AH ⏊ α
M
H
α
24.
A∆AHM:
AH ⏊ α
АН — катет
АM — гипотенуза
M
H
α
AH < AM
25.
AM
H
K
P
α
26.
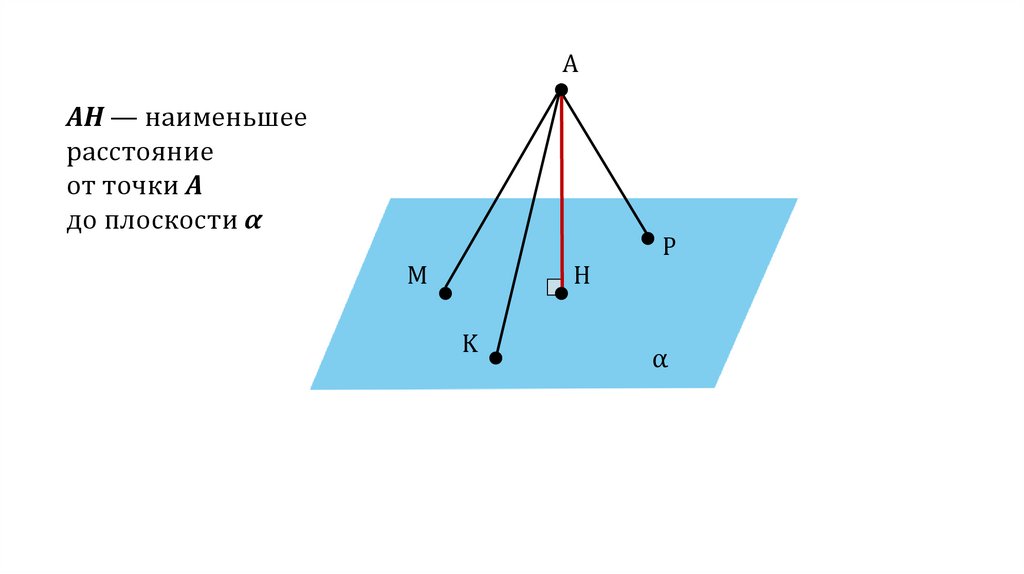
AAH — наименьшее
расстояние
от точки A
до плоскости α
M
H
K
P
α
27.
ОпределениеРасстоянием от точки А до плоскости α называется
длина перпендикуляра АН, проведённого
к плоскости α
A
H
α
28.
ЗадачаДано: AO ⏊ α
AO = 3 ед.
AM = АН = 5 ед.
Найти: MN
Решение:
∆АОМ: ОМ² = АМ² – АО²
ОМ² = 25 – 9 = 16
МН = 2 · ОМ = 2 · 4 = 8 (ед.)
Ответ: МН = 8 ед.
A
5
M
3
O
5
H
α
29.
Замечание 1Пусть даны две параллельные плоскости α и β. Тогда все
точки плоскости α будут равноудалены от плоскости β
A
M
α
AH ∥ MO
β
H
O
30.
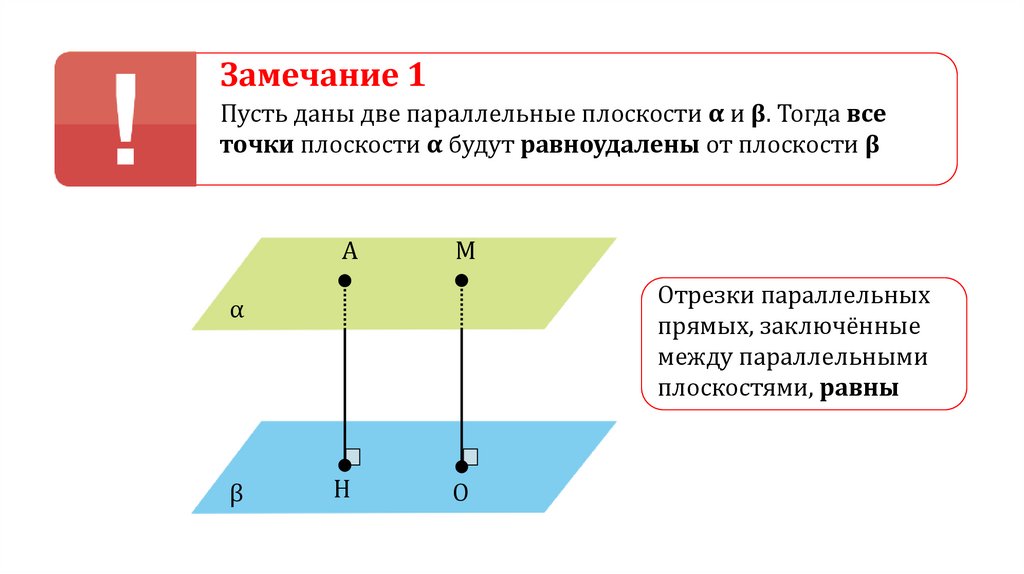
Замечание 1Пусть даны две параллельные плоскости α и β. Тогда все
точки плоскости α будут равноудалены от плоскости β
A
M
Отрезки параллельных
прямых, заключённые
между параллельными
плоскостями, равны
α
β
H
O
31.
ОпределениеРасстоянием между параллельными плоскостями называется
расстояние от произвольной точки одной из параллельных
плоскостей до другой
A
M
H
O
α
β
32.
ОпределениеРасстоянием между параллельными плоскостями называется
расстояние от произвольной точки одной из параллельных
плоскостей до другой
A
M
H
O
α
β
33.
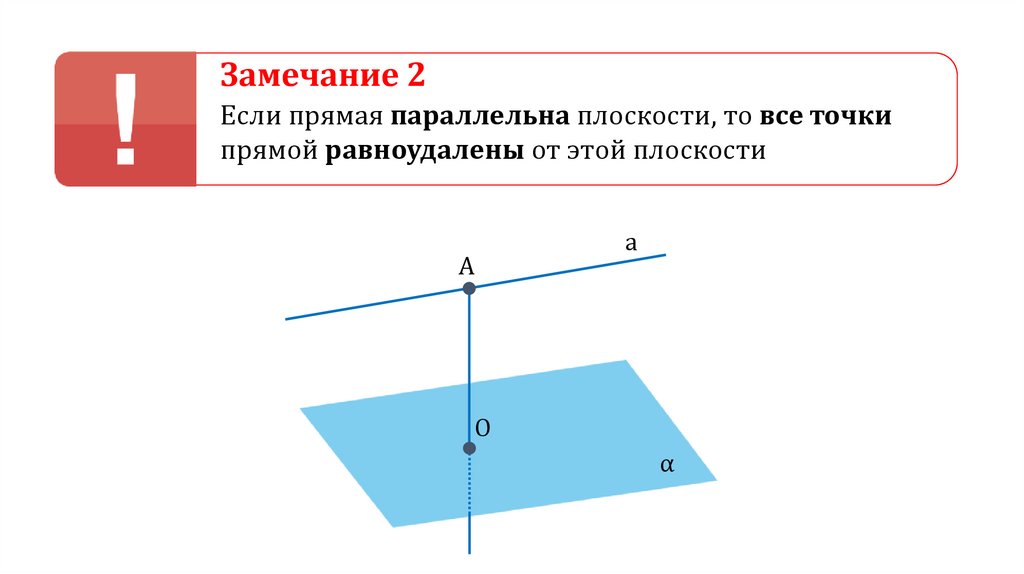
Замечание 2Если прямая параллельна плоскости, то все точки
прямой равноудалены от этой плоскости
a
A
O
α
34.
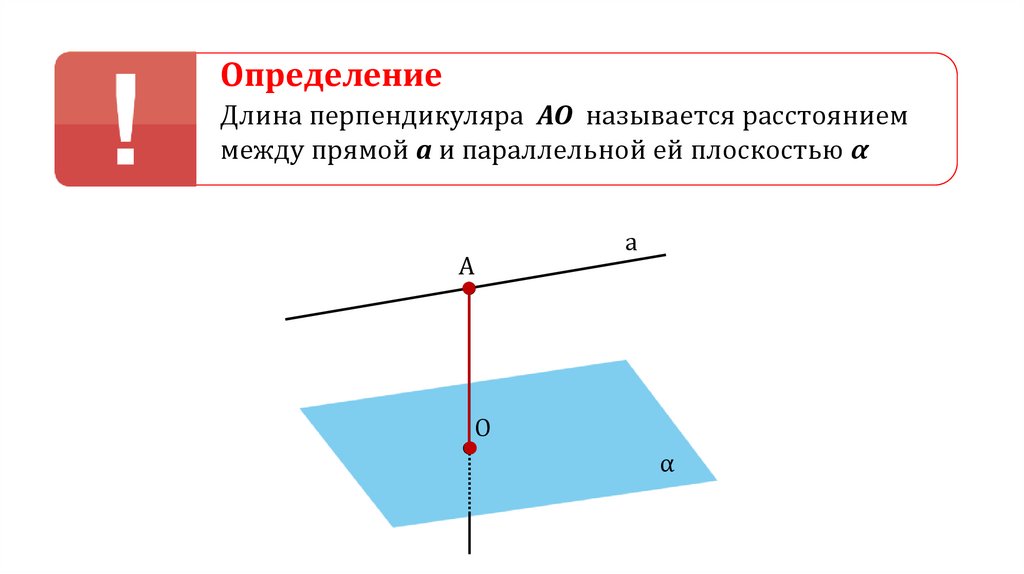
ОпределениеДлина перпендикуляра АО называется расстоянием
между прямой а и параллельной ей плоскостью α
a
A
O
α
35.
ОпределениеДлина перпендикуляра АО называется расстоянием
между прямой а и параллельной ей плоскостью α
a
A
O
α
36.
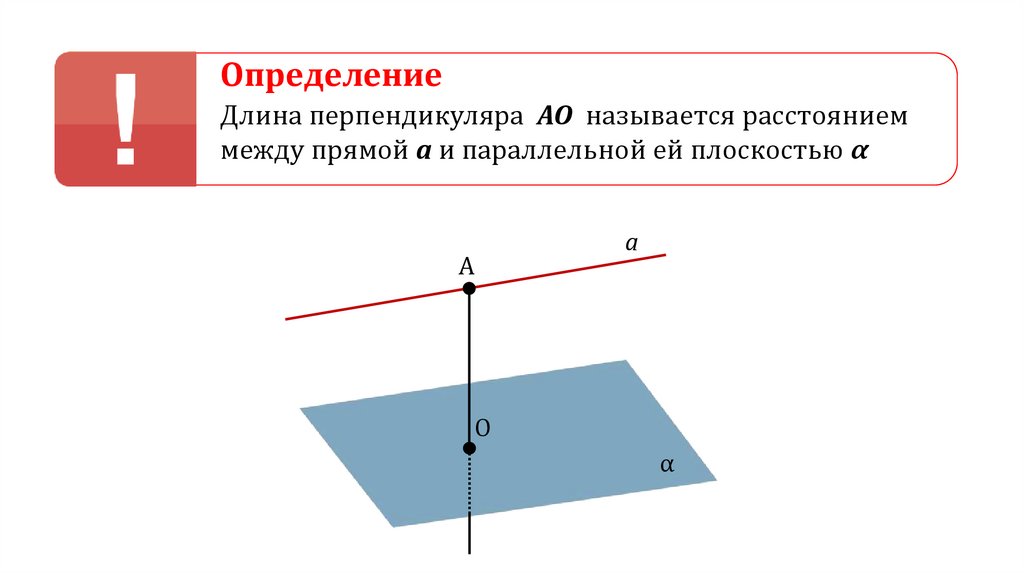
ОпределениеДлина перпендикуляра АО называется расстоянием
между прямой а и параллельной ей плоскостью α
a
A
O
α
37.
ЗадачаДано:
МН ∥ ABCD
МН = 6 см
∠МНО = 45°
B
Найти: MO
Решение:
∆MHO — прямоуг.
tg ∠МНО = MO ∶ MH ⇒
⇒ МO = MH · tg ∠МНО
МО = tg 45° · 6 = 1 · 6 = 6 (см)
Ответ: МО = 6 см
H
M
6 см
45°
C
O
D
A
38.
Замечание 3Пусть прямые а и b скрещивающиеся. Тогда плоскость α,
проходящая через прямую а, параллельна прямой b
b
a
α
39.
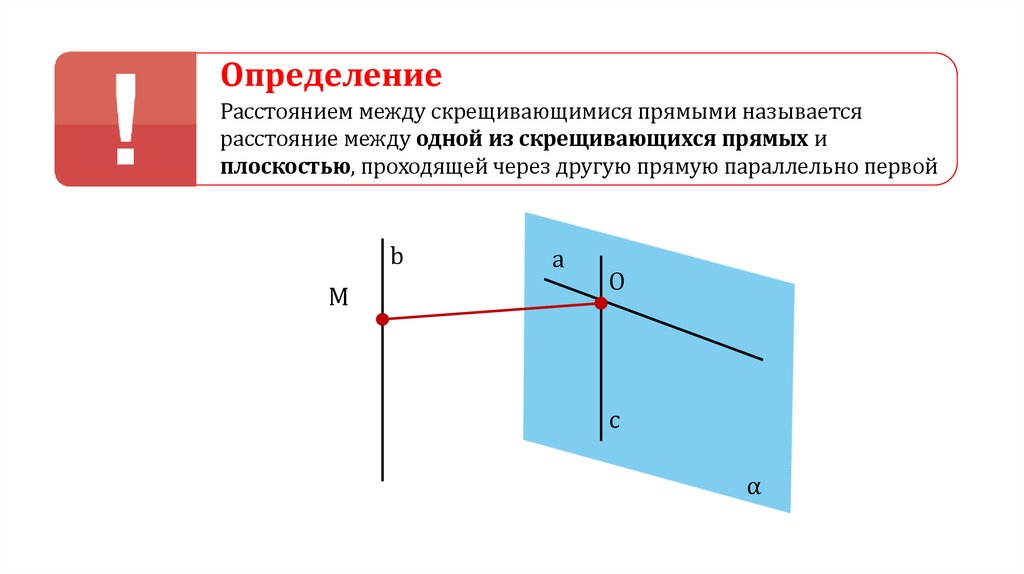
ОпределениеРасстоянием между скрещивающимися прямыми называется
расстояние между одной из скрещивающихся прямых и
плоскостью, проходящей через другую прямую параллельно первой
b
M
a
O
c
α
40.
ПланиметрияСтереометрия
А
А
а
М
Н
Н
М
a
Из всех расстояний от точки А до
различных точек прямойплоскости
а
наименьшим является длина
перпендикуляра.
Расстояние от точки до
Расстояние от точки до
прямой – длина
плоскости – длина
перпендикуляра
перпендикуляра
a
41.
Расстояние от лампочки до землиизмеряется по перпендикуляру,
проведенному от лампочки к
плоскости земли
42.
Если две плоскости параллельны, то все точки однойплоскости равноудалены от другой плоскости.
b
a II b
a
Расстояние от произвольной точки одной из параллельных
плоскостей до другой плоскости называется
расстоянием между параллельными плоскостями.
43.
Если прямая параллельна плоскости, то все точки прямойравноудалены от этой плоскости.
a
a II b
b
Расстояние от произвольной точки прямой до плоскости
называется расстоянием между прямой и параллельной ей
плоскостью.
44.
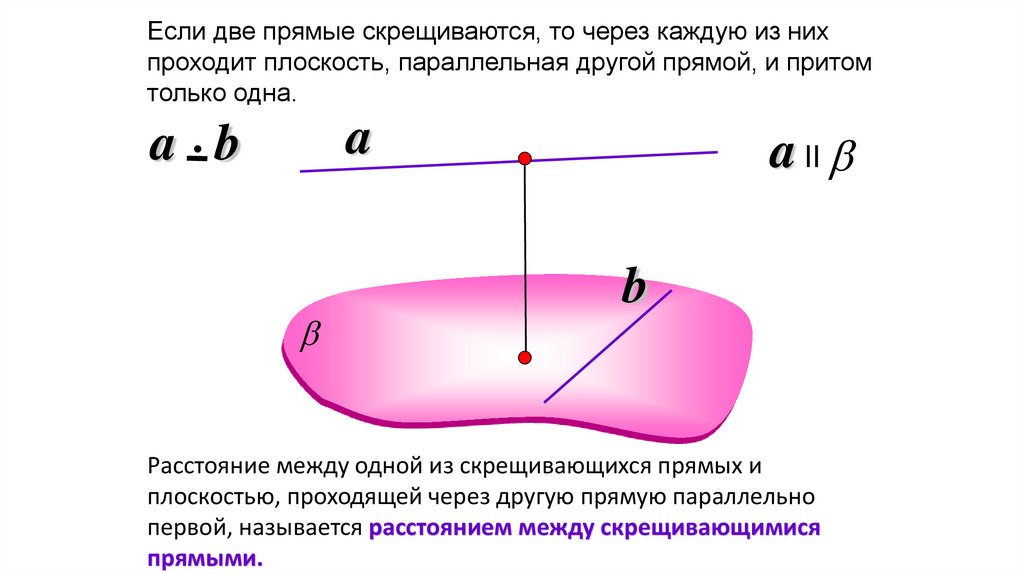
Если две прямые скрещиваются, то через каждую из нихпроходит плоскость, параллельная другой прямой, и притом
только одна.
a
a b
b
a II b
b
Расстояние между одной из скрещивающихся прямых и
плоскостью, проходящей через другую прямую параллельно
первой, называется расстоянием между скрещивающимися
прямыми.
45.
РасстояниеОтрезок, имеющий
между одной
концы
из на
скрещивающихся
двух скрещивающихся
прямых прямых
и
и
плоскостью,
перпендикулярный
проходящей
к этим
через
прямым,
другуюназывается
прямую параллельно
их общим
первой,
перпендикуляром.
называется расстоянием между скрещивающимися
прямыми.
На рисунке АВ – общий перпендикуляр.
В
А
46.
ВП-Р
Н-Я
П-Я
А
С
Н-Я
П-Я
M
47.
№1 Из точки А к плоскостипроведены две наклонные,
которые образуют со своими проекциями на плоскость
углы в 600. Угол между наклонными 900. Найдите
расстояние между основаниями наклонных, если
расстояние от точки А до плоскости равно 18 см.
A
18
К
В
600
600
48.
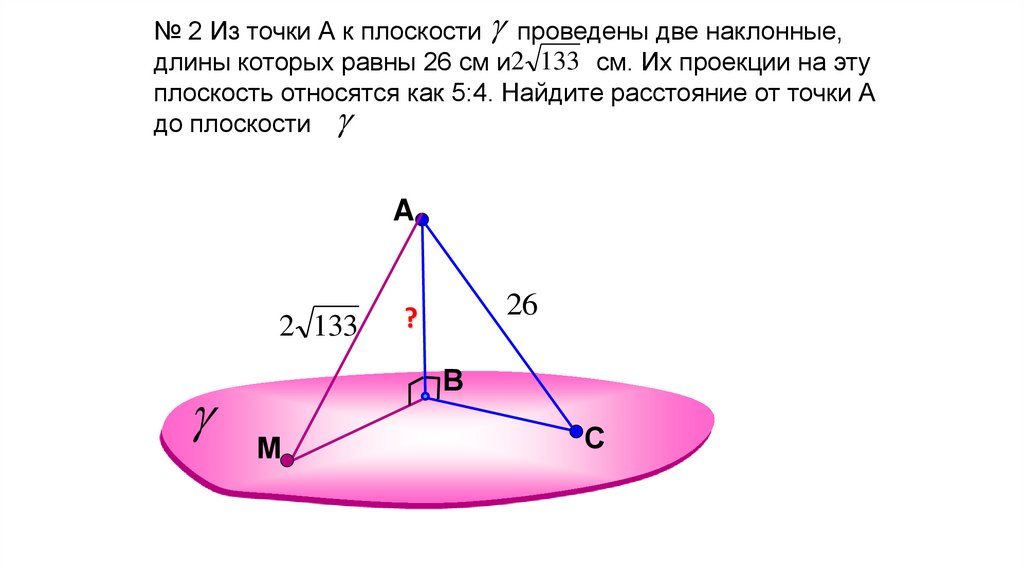
№ 2 Из точки А к плоскости проведены две наклонные,длины которых равны 26 см и2 133 см. Их проекции на эту
плоскость относятся как 5:4. Найдите расстояние от точки А
до плоскости .
A
2 133
26
?
В
М
С
49.
Теорема о трех перпендикулярах.Прямая, проведенная в плоскости через основание
наклонной перпендикулярно к ее проекции на эту
плоскость, перпендикулярна и к самой наклонной.
А
П-Р
a
Н
Н-я
П-я
М
a
50.
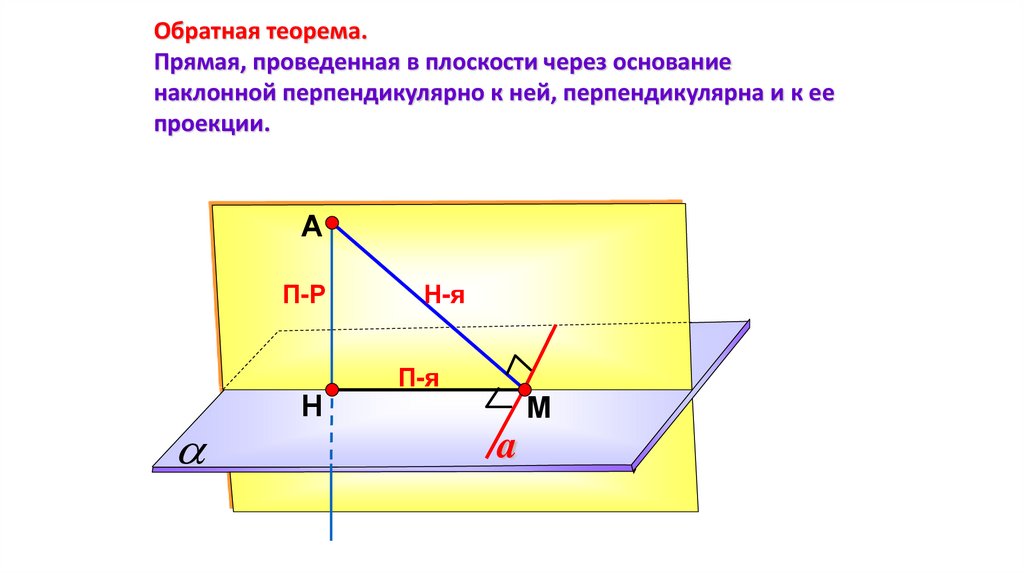
Обратная теорема.Прямая, проведенная в плоскости через основание
наклонной перпендикулярно к ней, перпендикулярна и к ее
проекции.
А
П-Р
a
Н
Н-я
П-я
М
a
51.
№ 3 Прямая АК перпендикулярна к плоскости правильноготреугольника АВС, а точка М – середина стороны ВС.
Докажите, что МК ^ ВС.
К
П-Р
А
В
П-я
М
С
BC ^AМ
П-я
BC ^MК
TTП
Н-я
52.
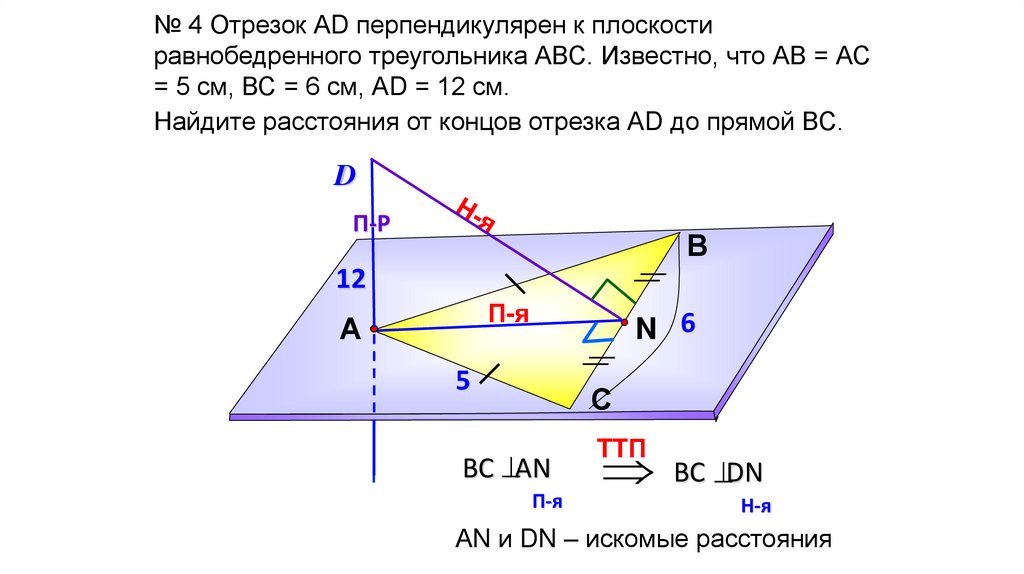
№ 4 Отрезок АD перпендикулярен к плоскостиравнобедренного треугольника АВС. Известно, что АВ = АС
= 5 см, ВС = 6 см, АD = 12 см.
Найдите расстояния от концов отрезка АD до прямой ВС.
D
П-Р
В
12
П-я
А
N 6
5
С
BC ^AN
П-я
BC ^DN
TTП
Н-я
АN и DN – искомые расстояния
53.
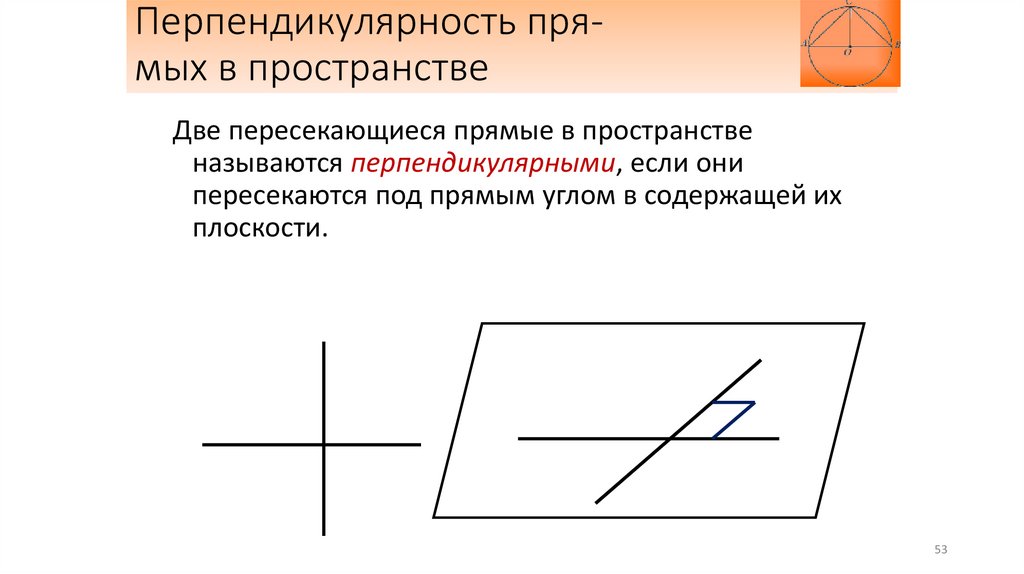
Перпендикулярность прямых в пространствеДве пересекающиеся прямые в пространстве
называются перпендикулярными, если они
пересекаются под прямым углом в содержащей их
плоскости.
53
54.
Перпендикулярные прямыеДве скрещивающиеся прямые называются перпендикулярными,
если параллельные им пересекающиеся прямые
перпендикулярны.
b
b’
А
a
54
55.
ПримерНазовите все прямые, перпендикулярные AD.
55
56.
ВопросКак показать, что
прямые АС и B’D’
перпендикулярны?
56
57.
ТеоремаЕсли две пересекающиеся прямые соответственно
параллельны двум перпендикулярным прямым, то
они тоже перпендикулярны.
Доказательство в Погорелове в параграфе
«Перпендикулярность прямых и плоскостей»,
теорема 17.1
57
58.
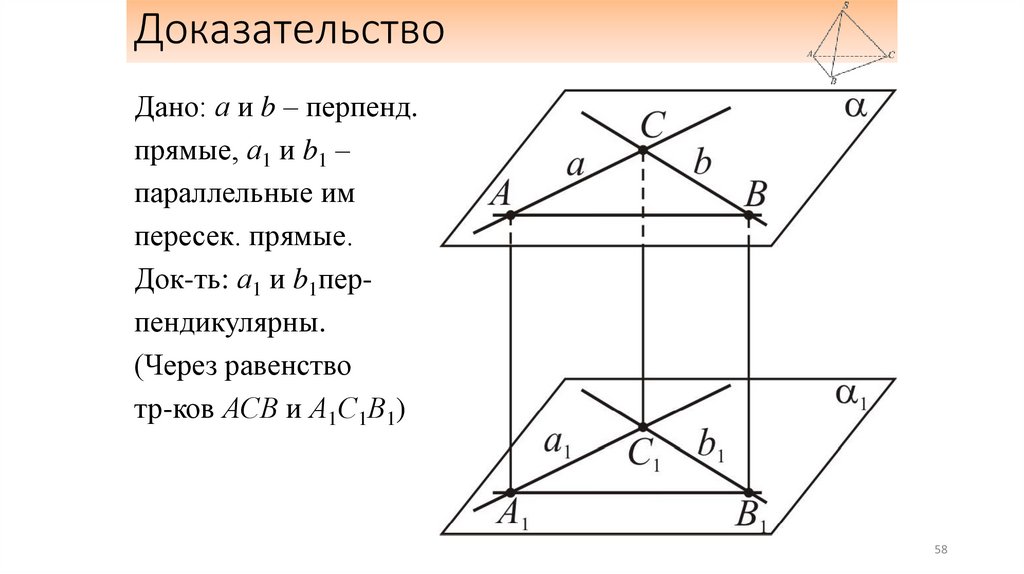
ДоказательствоДано: а и b – перпенд.
прямые, а1 и b1 –
параллельные им
пересек. прямые.
Док-ть: а1 и b1перпендикулярны.
(Через равенство
тр-ков АСВ и А1С1В1)
58
59.
1. Задача на построениеМожно ли через любую точку прямой в пространстве провести
перпендикулярную ей прямую?
Если да, то сколько?
59
60.
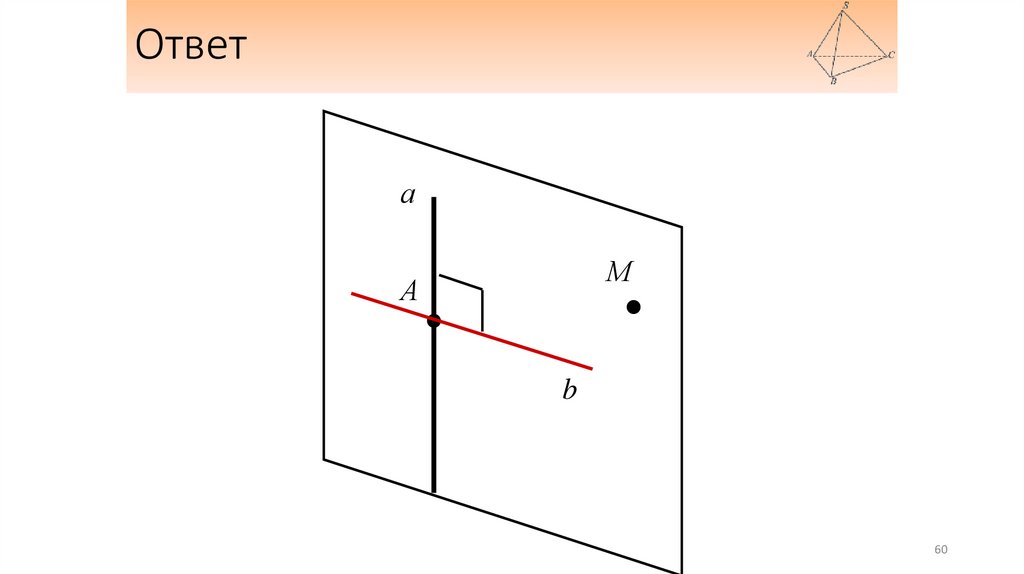
Ответа
М
А
b
60
61.
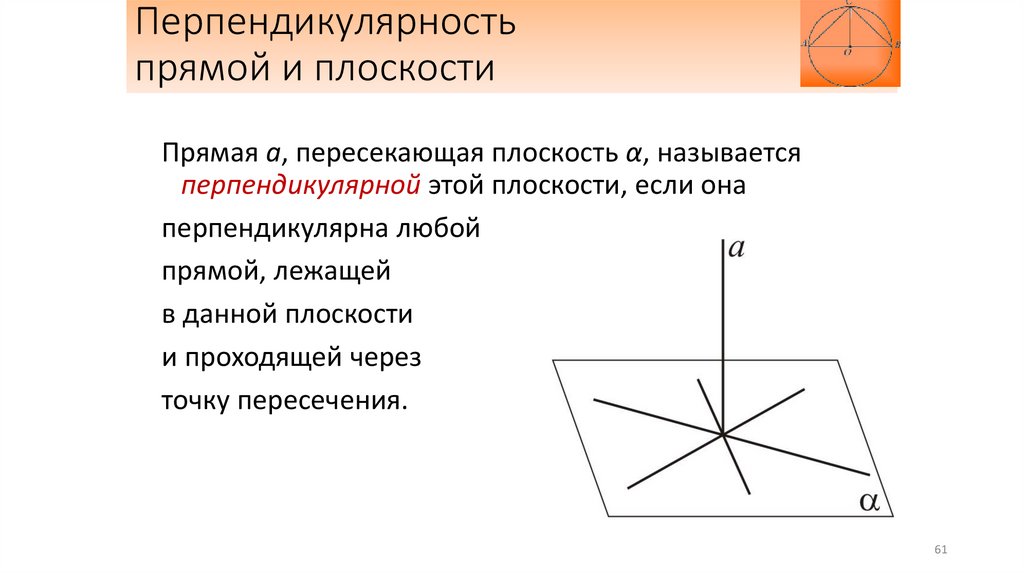
Перпендикулярностьпрямой и плоскости
Прямая а, пересекающая плоскость α, называется
перпендикулярной этой плоскости, если она
перпендикулярна любой
прямой, лежащей
в данной плоскости
и проходящей через
точку пересечения.
61
62.
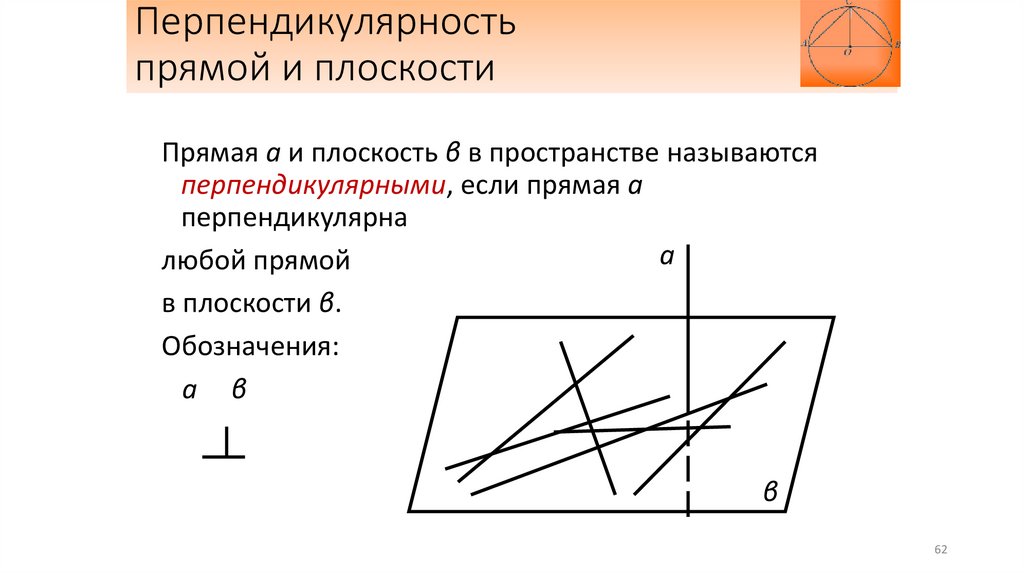
Перпендикулярностьпрямой и плоскости
Прямая а и плоскость β в пространстве называются
перпендикулярными, если прямая а
перпендикулярна
а
любой прямой
в плоскости β.
Обозначения:
а β
β
62
63.
Перпендикулярность прямой и плоскости обозначается знаком.
63
64.
Признак перпендикулярности прямой иплоскости
Если две пересекающие прямые, лежащие в
плоскости β, перпендикулярны прямой а, то а
β.
Другая формулировка.
Если прямая перпендикулярна двум
пересекающимся прямым, лежащим в плоскости,
то она перпендикулярна данной плоскости.
64
65.
Свойства перпендикулярной прямой иплоскости
Т.1. Если плоскость перпендикулярна одной из
двух параллельных прямых, то
a2
она перпендикулярна
a1
и другой.
Дано: а1| | a2; α а1.
Док-ть: α а2.
a
(Ссылка на теорему
x2
A2
b
A1
со слайда 8)
x1
65
66.
Свойства перпендикулярной прямой и плоскостиТ.1. Если плоскость перпендикулярна одной из двух
параллельных прямых, то
она перпендикулярна и другой.
Дано: а1| | a2; α а1.
a2
a1
Док-ть: α а2.
Если две пересекающиеся прямые
соответственно параллельны
двум перпендикулярным
прямым, то они тоже
b
перпендикулярны.
a
A1
x2
A2
x1
66
67.
Свойства перпендикулярной прямой иплоскости
Т.2. Две прямые, перпендикулярные одной
и той же плоскости,
параллельны.
Дано: а α , b α .
Док-ть: а | | b.
От противного.
a
См. теорему 17.4 (стр. 257)
a
C
b’
b
B
B’
67
68.
Теорема 3. Если прямаяперпендикулярна одной из
двух параллельных
плоскостей, то она
перпендикулярна и другой
плоскости.
68
69.
Обратное утверждениеВерно обратное свойство.
Если прямая перпендикулярна двум различным плоскостям, то эти
плоскости параллельны.
69
70.
Теорема о трех перпендикулярахПрямая теорема. Прямая, проведенная
на плоскости через основание наклонной перпендикулярно ее проекции,
перпендикулярна и самой наклонной.
А
А’
β
α
с
В
C
70
71.
Доказательство прямой теоремыПрямая, проведенная на плоскости через основание
наклонной перпендикулярно ее проекции,
А
перпендикулярна и самой наклонной.
Дано: АВ
Док-ть: с
α, с
АС.
А’
СВ.
β
α
В
с
C
71
72.
Обратная теоремаЕсли прямая на плоскости перпендикулярна
наклонной, то она
А’
перпендикулярна
β
проекции наклонной
на эту плоскость.
α
А
В
с
C
72
73.
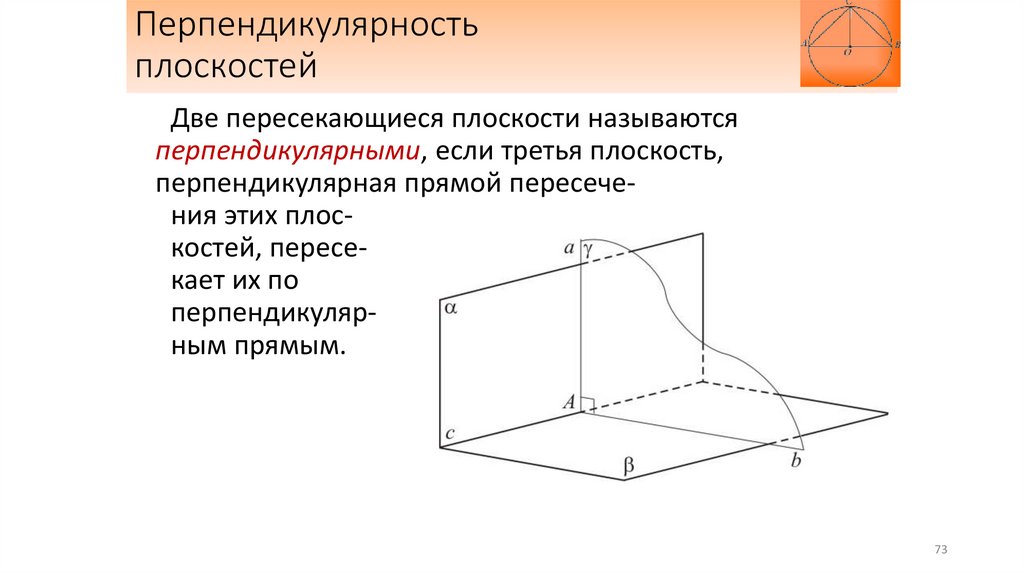
Перпендикулярностьплоскостей
Две пересекающиеся плоскости называются
перпендикулярными, если третья плоскость,
перпендикулярная прямой пересечения этих плоскостей, пересекает их по
перпендикулярным прямым.
73
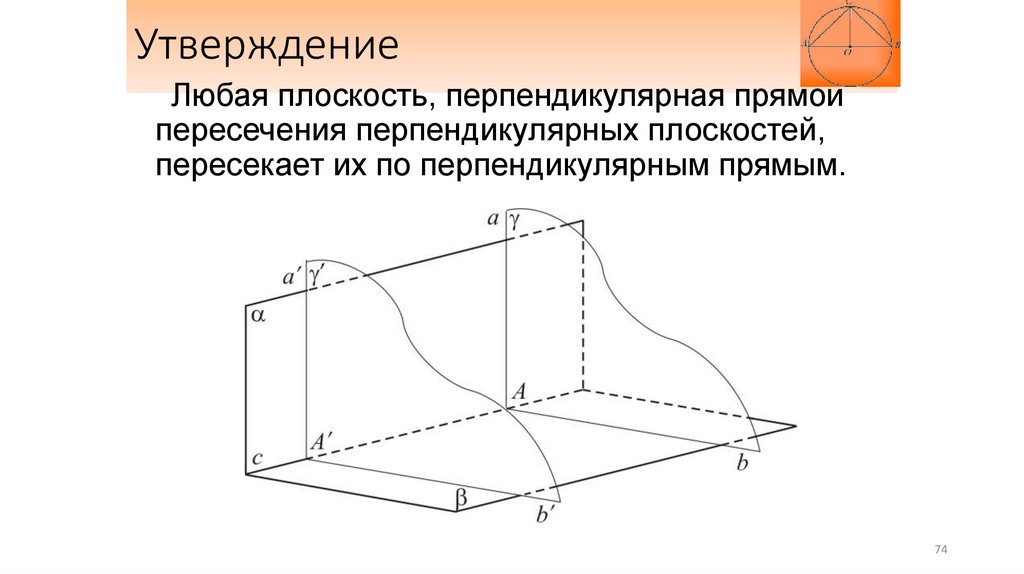
74.
УтверждениеЛюбая плоскость, перпендикулярная прямой
пересечения перпендикулярных плоскостей,
пересекает их по перпендикулярным прямым.
74
75.
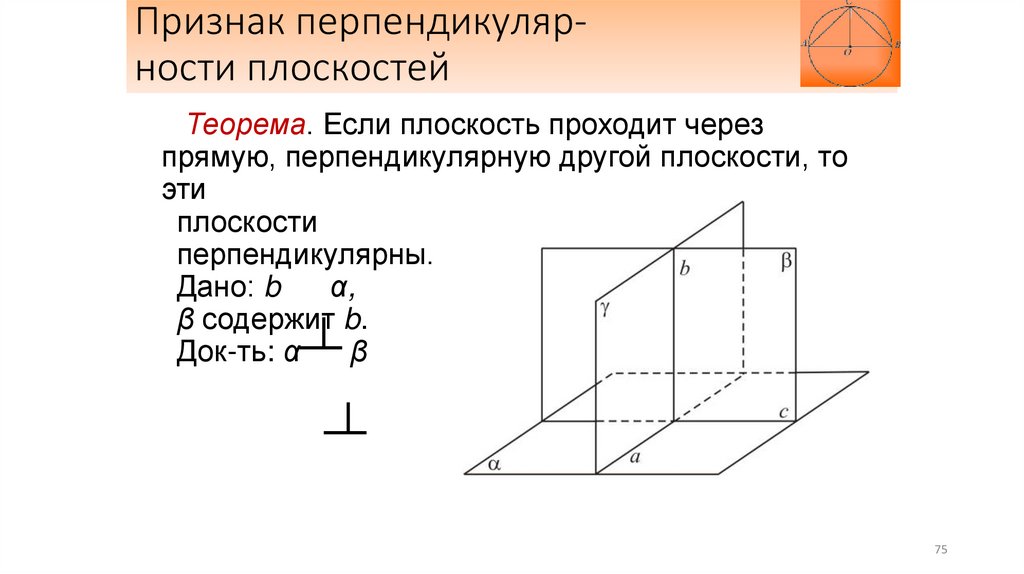
Признак перпендикулярности плоскостейТеорема. Если плоскость проходит через
прямую, перпендикулярную другой плоскости, то
эти
плоскости
перпендикулярны.
Дано: b
α,
β содержит b.
Док-ть: α
β
75
76.
Теорема о прямой, перпендикулярной линиипересечения двух взаимно
перпендикулярных плоскостей
Если в одной из двух перпендикулярных плоскостей
проведена прямая перпенди-кулярно их линии
пересечения, то эта прямая перпендикулярна другой
плоскости.
Дано: пл-ти α ^ β; пр. с = α β; пр. а ^ с
Доказать: прямая а ^ пл-ти α.
76
77.
ДоказательствоДано: пл-ти α ^ β; пр. с = α β; пр. а ^ с.
Доказать: прямая а перпендикулярна
плоскости α.
β
a
с
А
α
b
77
78.
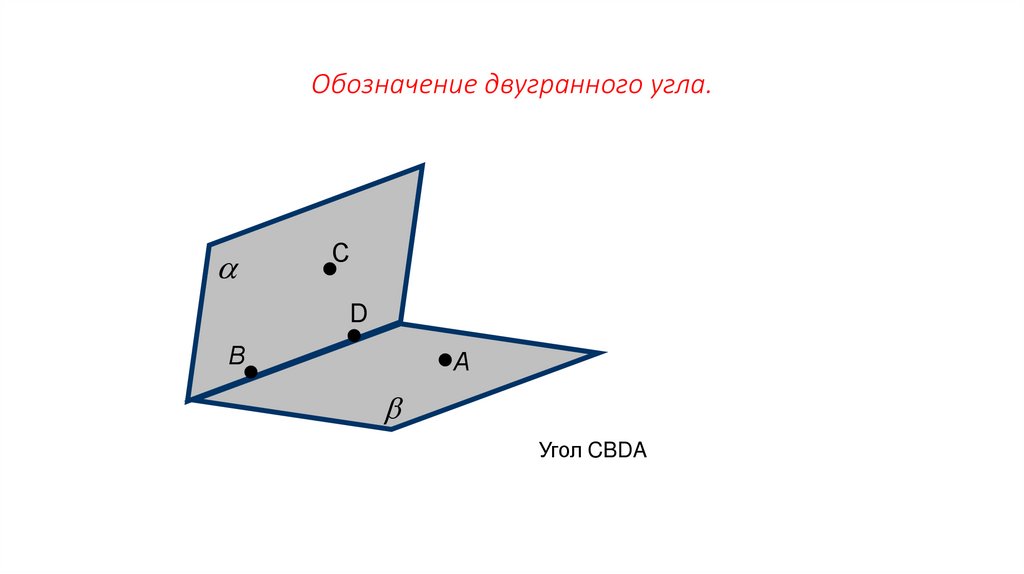
Обозначение двугранного угла.a
С
D
В
А
b
Угол CBDA
79.
Измерение двугранных углов. Линейный угол.Величиной двугранного угла называется величина его
линейного угла.
В
Р
М
АВМС = Р
А
С
D
Угол Р – линейный угол двугранного угла АВМС
80.
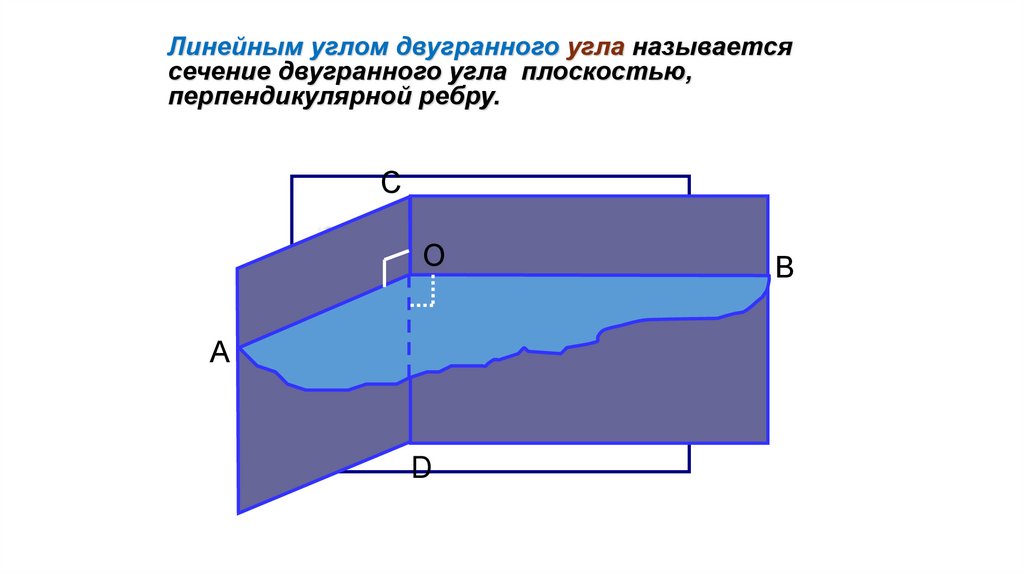
Линейным углом двугранного угла называетсясечение двугранного угла плоскостью,
перпендикулярной ребру.
С
О
А
D
В
81.
Способ нахождения (построения) линейного угла.1. Найти ( увидеть) ребро и грани двугранного
угла
2. В гранях найти направления ( прямые)
перпендикулярные ребру
3. (при необходимости) заменить выбранные
направления параллельными им лучами с общим
началом на ребре двугранного угла
При изображении сохраняется параллельность и
отношение длин параллельных отрезков
82.
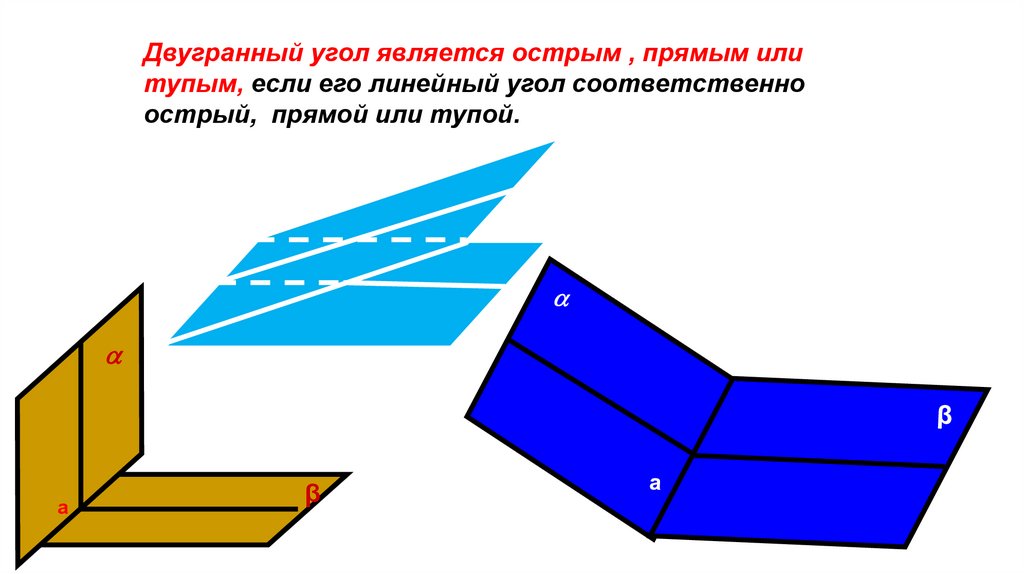
Двугранный угол является острым , прямым илитупым, если его линейный угол соответственно
острый, прямой или тупой.
β
a
а
a
β
83.
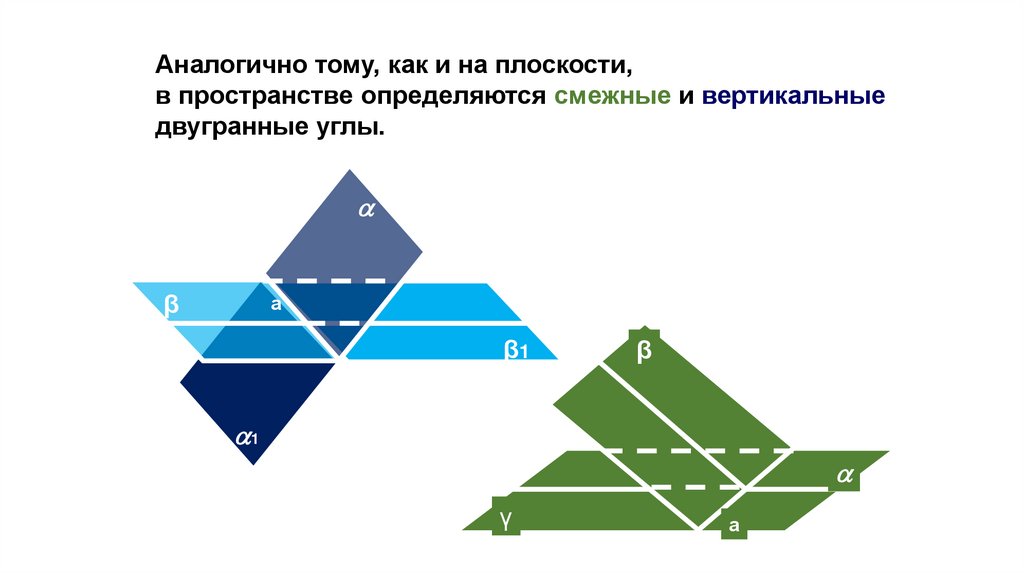
Аналогично тому, как и на плоскости,в пространстве определяются смежные и вертикальные
двугранные углы.
a
β
а
β1
β
a1
a
γ
а
84.
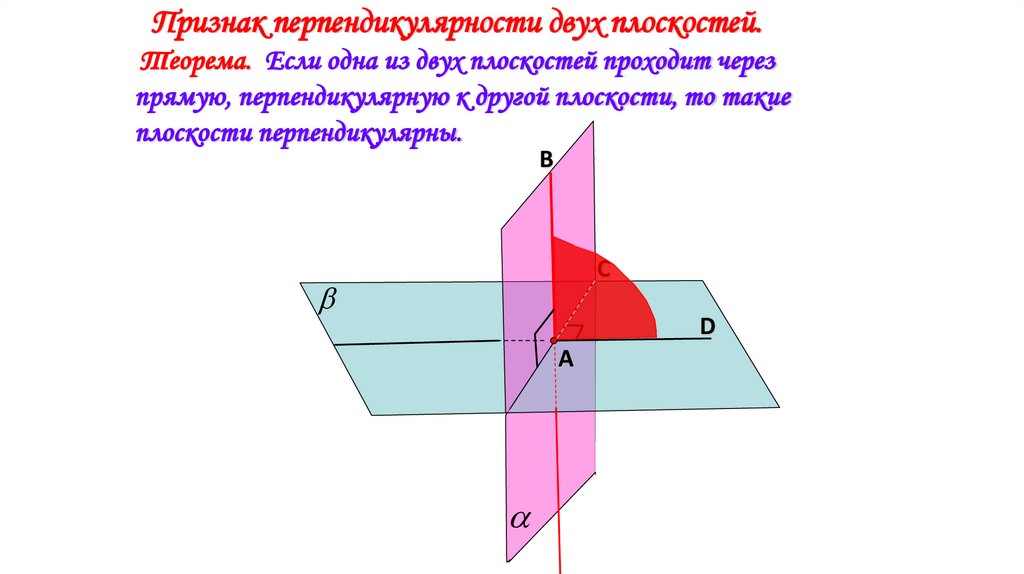
Признак перпендикулярности двух плоскостей.Теорема. Если одна из двух плоскостей проходит через
прямую, перпендикулярную к другой плоскости, то такие
плоскости перпендикулярны.
В
С
b
D
А
a
85.
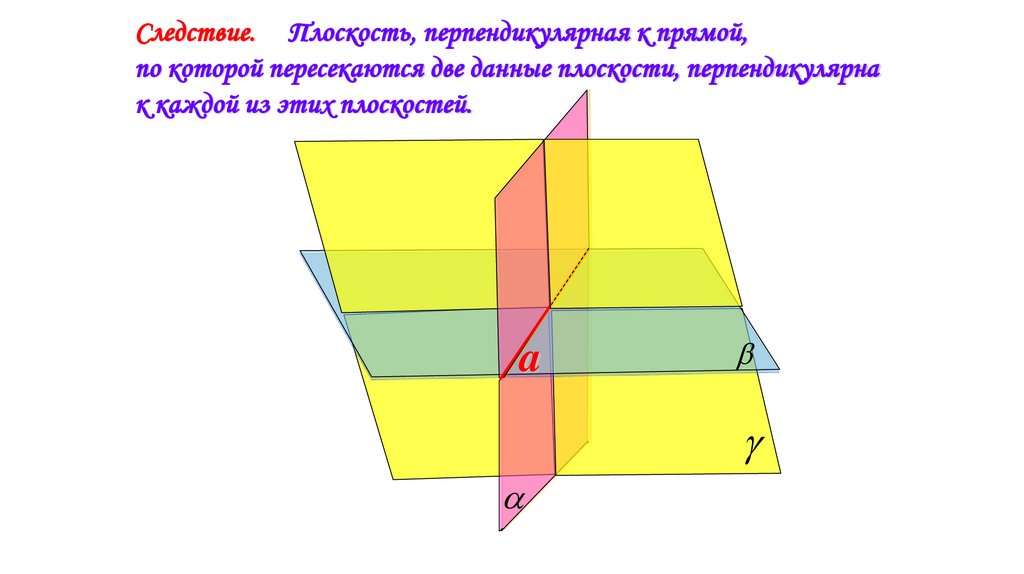
Следствие. Плоскость, перпендикулярная к прямой,по которой пересекаются две данные плоскости, перпендикулярна
к каждой из этих плоскостей.
a
b
a
86.
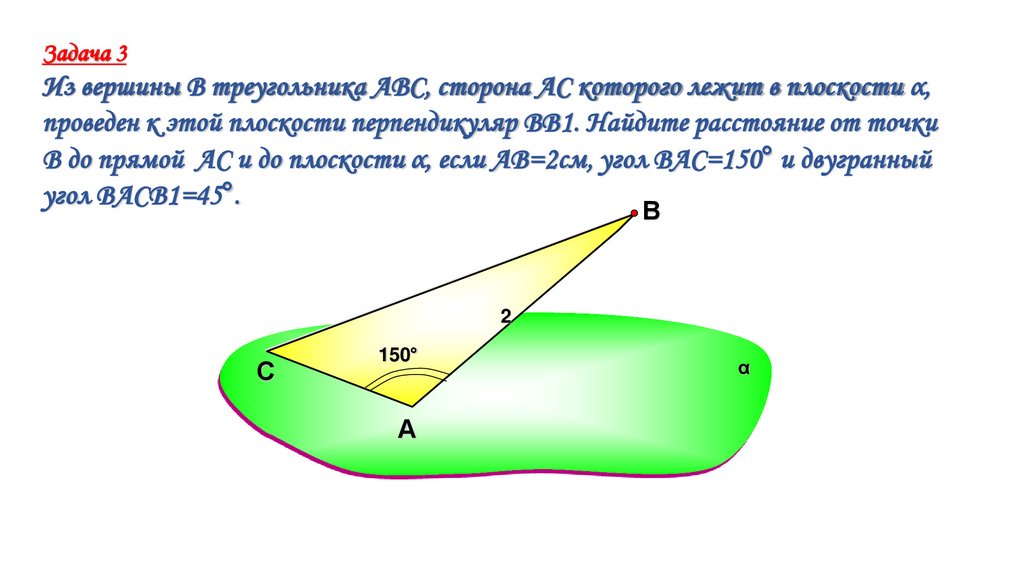
Задача 3Из вершины В треугольника АВС, сторона АС которого лежит в плоскости α,
проведен к этой плоскости перпендикуляр ВВ1. Найдите расстояние от точки
В до прямой АС и до плоскости α, если АВ=2см, угол ВАС=150° и двугранный
угол ВАСВ1=45°.
В
2
С
150°
А
α
87.
Расположение плоскостей в пространстве.α и β совпадают
b
a
a
a
b
b
α β
α β
88.
Две плоскости называются параллельными, еслиони не пересекаются.
Плоскости
Пересекаются
Параллельны
α
β
α
β
α∩β
α || β
89.
90.
ab
91.
Признак параллельности плоскостейЕсли две пересекающиеся прямые одной плоскости
соответственно параллельны двум прямым другой
плоскости, то эти плоскости параллельны.
Дано:
• а α; в α; а∩в=М;
• а1 β; в1 β;
• а║а1; в║в1
• Доказать,
• что α || β
а М
b
а1 М
b1
α
β
1
92.
Доказательство от противного•а α; а1 β; а║а1 а║β
в α; в1 β; в║в1 в║β
•Пусть α ∩ β = с
•Тогда
•а || β, α ∩ β = с а || с.
•b || β, α ∩ β = с b || с.
•а ∩ в=М; а║с; и в║с а||b
а М
b
с
α
•Находим противоречие
β
условию: через точку М
проходят две прямые а и b,
параллельные прямой с.
•Предположение α ∩ β = с неверно
а1 М
1
b1
93.
Какие теоремы мы использовали при доказательстве признака?а α; а1 β; а║а1 а║β; в α;
в1 β; в║в1 в║β
Признак параллельности
прямой и плоскости
Пусть α ∩ β = с
Делаем предположение,
противное заключению
Тогда
а || β, α ∩ β = с а || с.
b || β, α ∩ β = с b || с.
Теорема о линии пересечения
плоскостей
а ∩ в=М; а║с; и в║с а||b
Теорема о параллельности
трех прямых в
пространстве
Находим противоречие условию:
через точку М проходят две
прямые а и b, параллельные прямой
с.
Теорема о параллельных
прямых
Предположение
α ∩ β = с - неверно
Делаем вывод, α || β
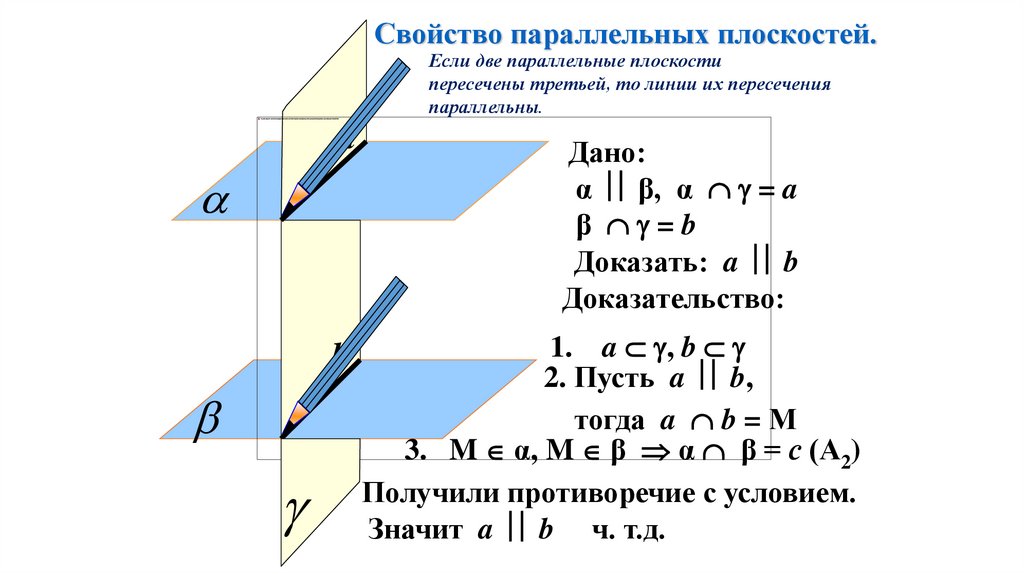
94.
Свойство параллельных плоскостей.Если две параллельные плоскости
пересечены третьей, то линии их пересечения
параллельны.
а
a
b
b
Дано:
α β, α = a
β =b
Доказать: a b
Доказательство:
1. a , b
2. Пусть a b,
тогда a b = М
3. M α, M β α β = с (А2)
Получили противоречие с условием.
Значит a b ч. т.д.
95.
Свойство параллельных плоскостей.a
А
b
В
Отрезки параллельных прямых,
заключенные между параллельными
плоскостями, равны.
С
Дано:
α β, АВ СD
АВ α = А, АВ β = В,
СD α = С, СD β = D
Доказать: АВ = СD
Доказательство:
D
1. Через АВ СD проведем
2. α β, α = a, β = b
3. АС В D,
4. АВ СD (как отрезки парал. прямых)
5. АВСД – параллелограмм (по опр.)
АВ = СD ( по свойству параллелограмма)
96.
aЕсли прямая а пересекает плоскость , то она пересекает
также любую плоскость, параллельную данной плоскости .
а
a
b
a
97.
aЕсли плоскость пересекает одну из параллельных плоскостей b и
то она пересекает и другую плоскость.
,
Дано:
α β, α пересекается с γ (рис)
a
Доказать: β пересекается с γ
а
Доказательство:
b
b
Пусть γ пересекает α по прямой а.
Проведем в плоскости γ прямую b,
пересекающую α.
Прямая b пересекает α, поэтому она
пересекает параллельную ей
плоскость β (задача № 55).
Следовательно, и плоскость γ, в
которой лежит прямая b, пересекает
плоскость β.
98.
Отрезок СD лежит в плоскости a. Концы отрезка ЕМ лежатна параллельных плоскостях a и b . Постройте линии
пересечения плоскостей ЕСD, ЕМС и ЕМD с плоскостью b .
Е
b
a
М
D
С
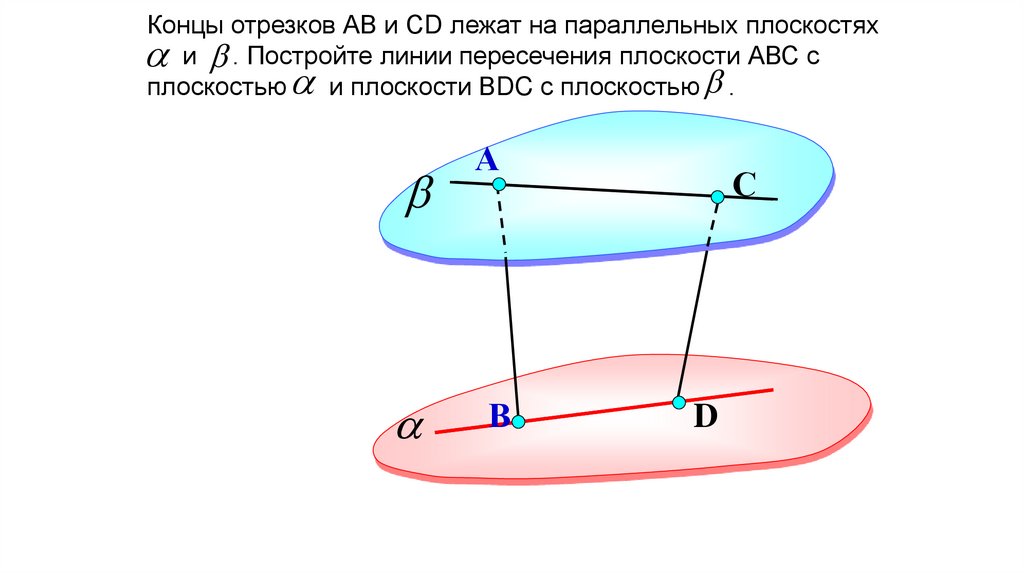
99.
Концы отрезков АВ и СD лежат на параллельных плоскостяхa и b . Постройте линии пересечения плоскости АВС с
плоскостью a и плоскости ВDC с плоскостью b .
b
a
А
В
С
D
100.
Отрезки АВ и СD лежат соответственно в параллельныхплоскостях a и b . Что можно сказать о взаимном
расположении прямых АD и ВС?
В
А
a
b
С
D
АD BC
101.
a и b параллельны, прямые a и b пересекаютсяв точке М. Прямая a пересекает плоскости a и b
Плоскости
соответственно в точках А и В, а прямая b пересекает
плоскость в точке А1.
М
Постройте точку
a
пересечения
b
a
прямой b с
плоскостью b .
Поясните.
A
a
A1
b
B
B
1
102.
Плоскостиa и b параллельны, aIIa1. Прямая a пересекает
a и b соответственно в точках А и В, а прямая a1
пересекает плоскость a в точке А1. Постройте точку
пересечения a1 с плоскостью b . Поясните.
A a
B
a1
A1
a
B1
b
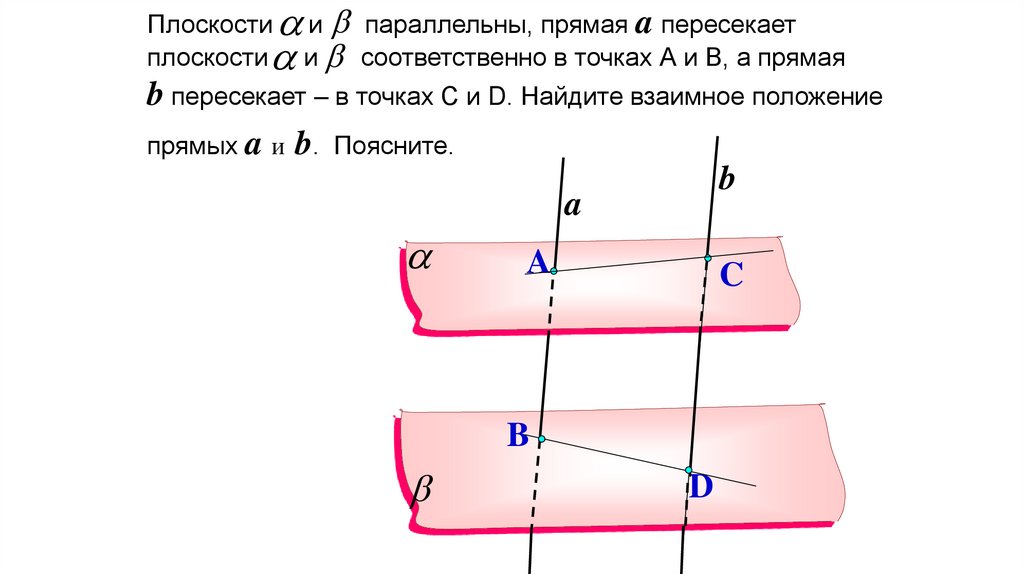
103.
a и b параллельны, прямая a пересекаетa и b соответственно в точках А и В, а прямая
Плоскости
плоскости
b пересекает – в точках С и D. Найдите взаимное положение
прямых a и b. Поясните.
b
a
a
A
C
B
b
D
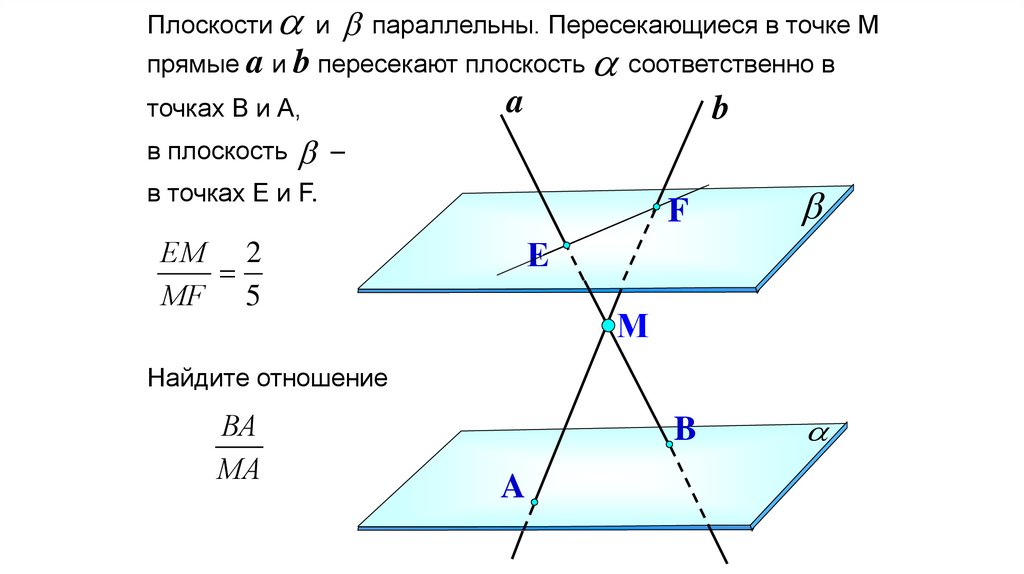
104.
a и b параллельны. Пересекающиеся в точке Мпрямые a и b пересекают плоскость a соответственно в
Плоскости
точках В и А,
a
b
в плоскость b –
в точках Е и F.
ЕМ 2
=
МF 5
F
b
B
a
Е
М
Найдите отношение
ВА
МА
A
105.
Тетраэдр ипараллелепипед
106.
Задача 1Как при помощи шести спичек сложить
четыре одинаковых треугольника?
Автор: Семёнова Елена Юрьевна
МОУ СОШ №5 – «Школа здоровья и развития» г. Радужный
107.
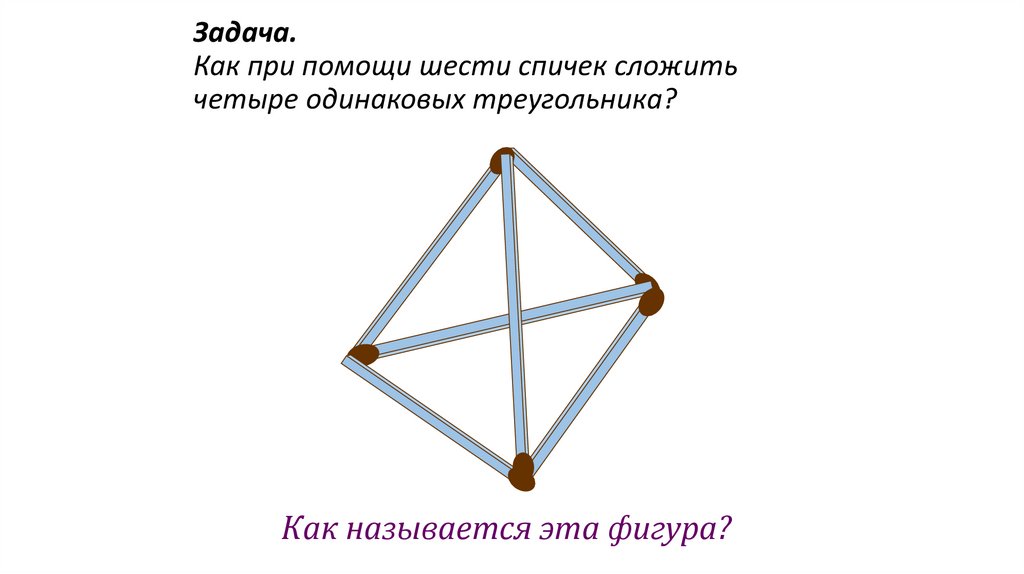
Задача.Как при помощи шести спичек сложить
четыре одинаковых треугольника?
Как называется эта фигура?
108.
Тетраэдр109.
Понятие тетраэдраS
С
А
В
Тетраэдр – (греч. tetréedro, от tetra, в сложных словах четыре и hedra – основание,
грань)
110.
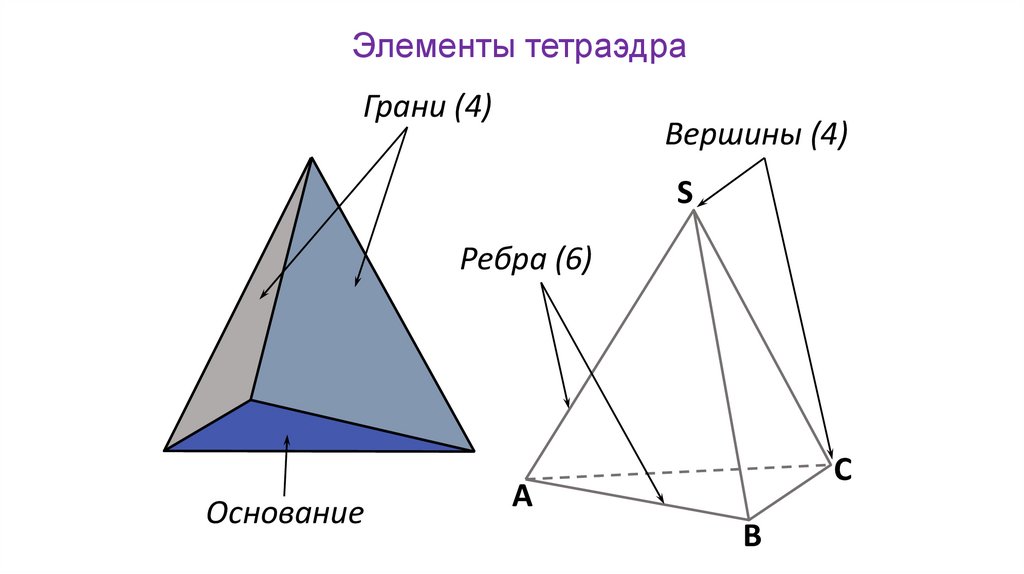
Элементы тетраэдраГрани (4)
Вершины (4)
S
Ребра (6)
Основание
С
А
В
111.
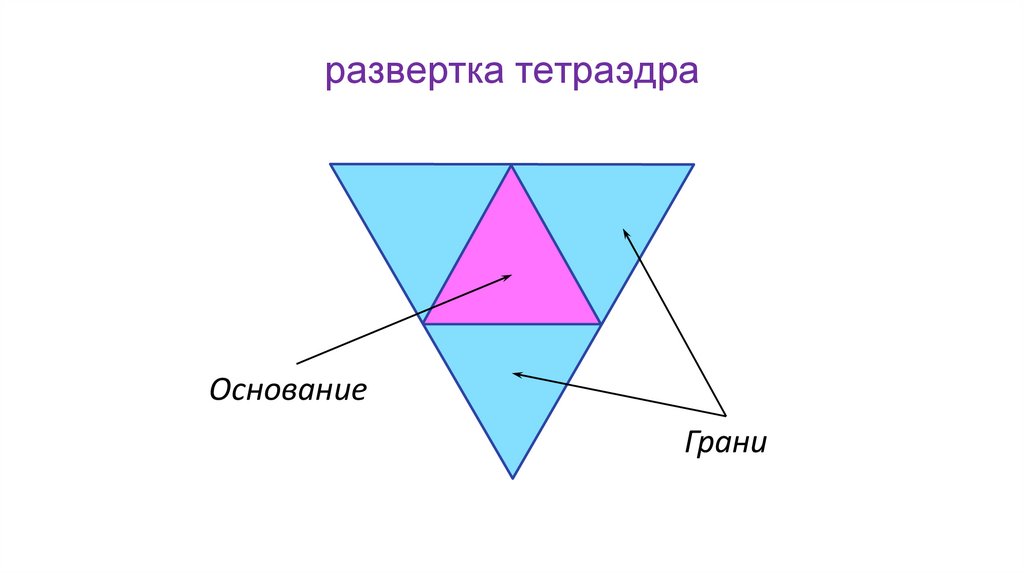
развертка тетраэдраОснование
Грани
112.
параллелепипед113.
Наклонный параллелепипедПараллелепипед (от греч. παράλλος − параллельный и греч. επιπεδον
−
плоскость)
− призма, основанием которой служит параллелограмм, или
многогранник, у которого шесть граней и каждая из них − параллелограмм.
114.
Основания (2)Ребра (12)
Вершины (8)
Боковые грани (4)
115.
Параллелепипед ABCDA1B1C1D1D1
C1
А1
B1
С
D
А
В
116.
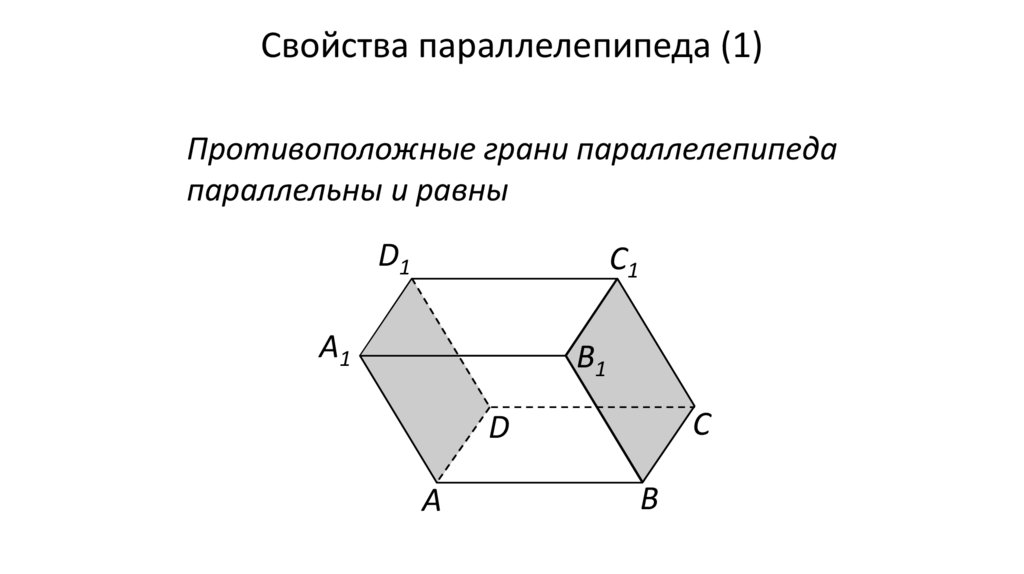
Свойства параллелепипеда (1)Противоположные грани параллелепипеда
параллельны и равны
D1
C1
А1
B1
С
D
А
В
117.
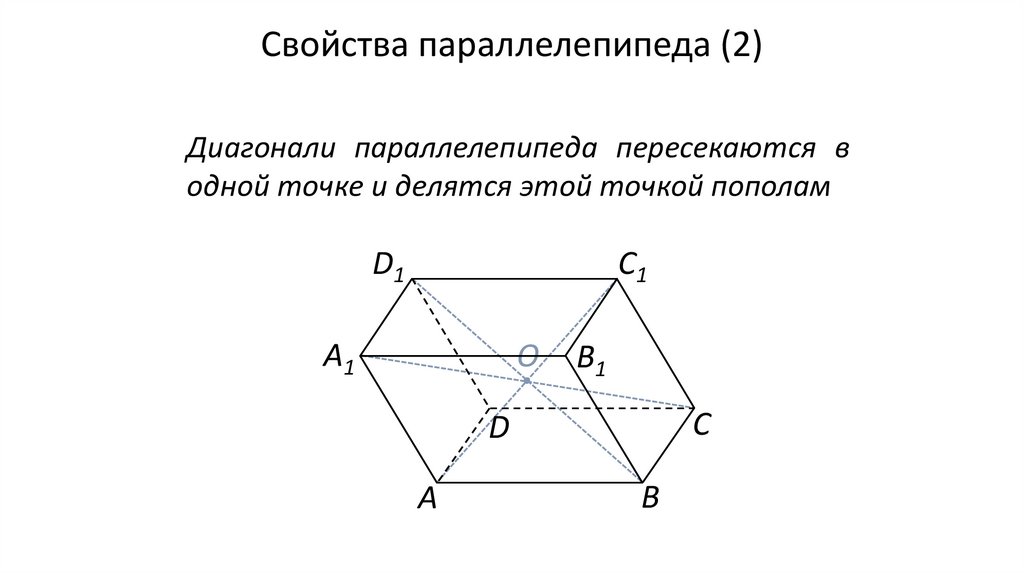
Свойства параллелепипеда (2)Диагонали параллелепипеда пересекаются в
одной точке и делятся этой точкой пополам
D1
C1
А1
О
B1
С
D
А
В
118.
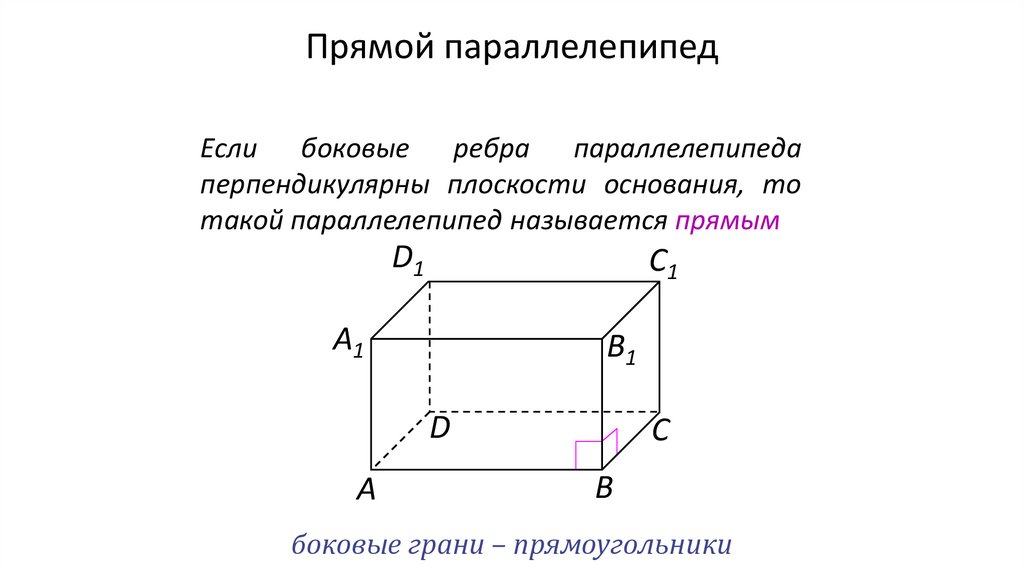
Прямой параллелепипедЕсли боковые ребра параллелепипеда
перпендикулярны плоскости основания, то
такой параллелепипед называется прямым
D1
C1
А1
B1
D
А
С
В
боковые грани – прямоугольники
119.
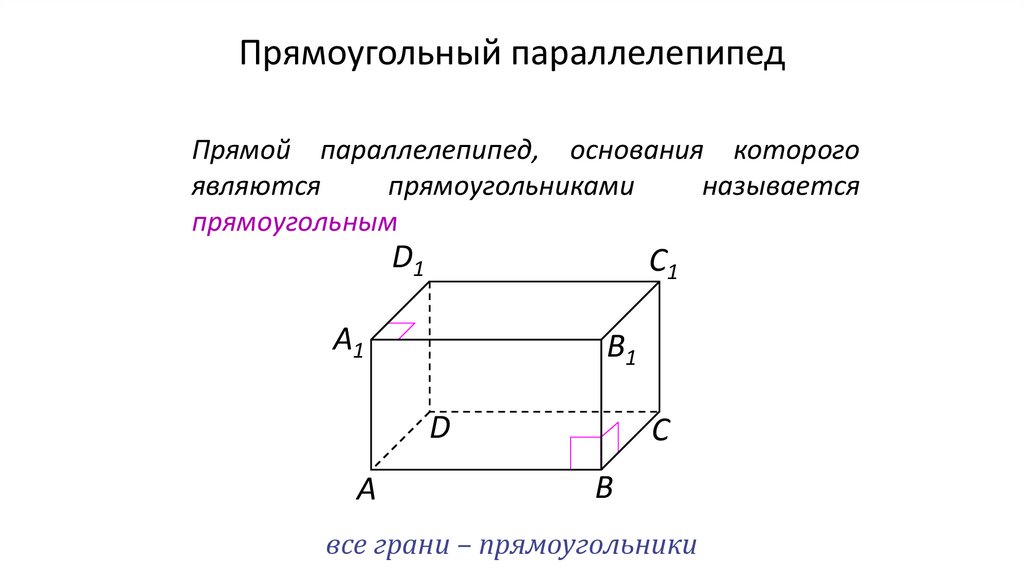
Прямоугольный параллелепипедПрямой параллелепипед, основания которого
являются
прямоугольниками
называется
прямоугольным
D1
C1
А1
B1
D
А
С
В
все грани – прямоугольники
120.
Свойства прямоугольногопараллелепипеда
1° В прямоугольном параллелепипеде все
шесть граней – прямоугольники
2° Все двугранные углы прямоугольного
параллелепипеда– прямые
121.
Прямоугольный параллелепипедДлины трех ребер, имеющих общую вершину,
назовем измерениями прямоугольного
параллелепипеда
D1
C1
А1
B1
D
А
С
В
длина, ширина и высота
122.
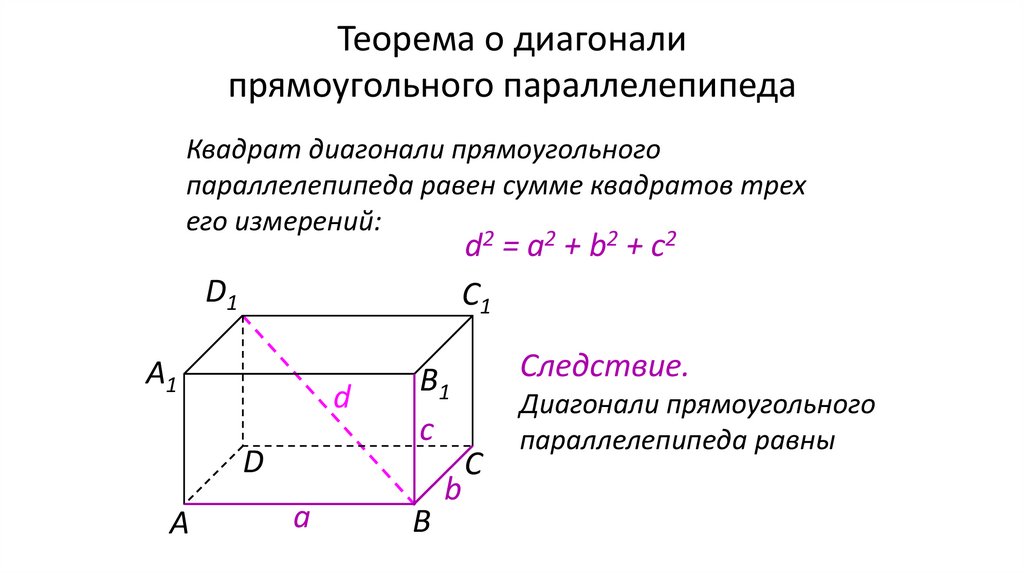
Теорема о диагоналипрямоугольного параллелепипеда
Квадрат диагонали прямоугольного
параллелепипеда равен сумме квадратов трех
его измерений:
d2 = a2 + b2 + c2
C1
D1
А1
d
D
А
a
Следствие.
B1
c
В
b
С
Диагонали прямоугольного
параллелепипеда равны










































































 Математика
Математика








