Параллельные алгоритмы

1.

федеральное государственное бюджетное образовательное учреждение высшего образования
«Вологодский государственный университет»
Институт математики, естественных и компьютерных наук
Кафедра автоматики и вычислительной техники
Общий отчет по дисциплине
«Параллельные алгоритмы»
Выполнил: Ломков С.А.
Группа: 4Б09 ПО-31
Руководитель профессор Горбунов В.А.
Вологда
2023 г.

2.

Лабораторная работа 1
Файловые системы MS DOS и Linux. Внутренние
команды.
Цель: Изучение составных частей MS DOS, архитектуры, внутренних команд.
Применение на практике команд MS DOS. Изучение операционной системы
Linux.
Задание: С помощью клавиши «Пуск», меню «Программы» выбрать и
запустить команду «Работа в MS DOS». Выбрать устройство "С:" (или другой
диск, по указанию преподавателя. например "Н:"). Для этого в командной строке
(там, где находится мигающий курсор) с клавиатуры ввести "С:" ("Н:" или др..).
Выполнить команды в MS DOS, продублировать эти же команды в Linux.

3.

Практическая часть
Для MS DOS
Запустили программу «Работа в MS DOS»
Ввели команду CLS и нажимаем enter. Команда очищает записи на экране.
С:\ >cls ↵
Ввели команду dir и нажали enter. Выводит содержимое директории. Dir/p выводит постранично, dir/w в расширенном формате.
С:\ >dir ↵ С:\ >dir /p ↵ С:\ >dir/w ↵
Ввели команду date, затем time. Данные совпадали с реальными поэтому мы нажимаем enter.
С:\ >date ↵ С:\ >time ↵
Ввели команду ver. Выводит данные о версии ОП.
С:\ >ver ↵
Ввели команду VOL. Выводит метку тома диска.
С:\ >vol ↵
Ввели команду md prim, где prim название директории. Создает папку с названием prim. Перешли в директорию командой cd prim,
посмотрели содержимое директории с помощью команлы dir.
С:\ >md prim ↵ С:\ >cd prim ↵ С:\ >dir ↵
Создали файл text1.txt командой copy con text1.txt . Ввели hello word нажали ctrl + z.
С:\ >copy con text1.txt ↵
Посмотрели содержимое фала text1.txt командой type.
С:\ >type text1.txt ↵
Создали два подкаталога t1 и t2 с помощью команды md и нажали enter. Проверили их создание командой dir.
С:\ >md t1 ↵ С:\ >md t2 ↵ С:\ >dir ↵
Перешли в подкаталог t1 и t2. Проверили содержимое каждого каталога.
С:\ >cd t1 ↵ С:\ >dir ↵ С:\ >cd.. ↵ С:\ >cd t2 ↵ С:\ >dir ↵ С:\ >cd.. ↵
Скопировали файл text1.txt из каталога prim в t1. Скопировали этот файл тот же каталог, но с другим расширением. Посмотрели
содержимое каталога t1.
С:\ >copy text1.txt C:\prim\t1\*.* ↵ С:\ >copy text1.txt C:\prim\t1\*.doc ↵
С:\ >dir t1 ↵
Скопировали два этих файла из подкаталога t1 в t2. Проверили содержимое каталога.
С:\ >cd t1 ↵ С:\ >copy *.* C:\prim\t2\*.* ↵ С:\ >dir↵
Исследовали возможности удаления каталогов. С помощью команды rd невозможно удалить каталог пока в нем имеются файлы.

4.

Практическая часть
Для MS DOS
Удалили файлы из каталога t1 c помощью команды del, до этого перейдя в нужную директорию. Проверили содержимое
каталога.
С:\ >cd t2 ↵ С:\ >del *.* ↵ С:\ >dir ↵ С:\ >cd.. ↵
Удалили подкаталог t2 с помощью команды rd t2. Проверили содержимое каталога prim.
С:\ >rd t2 ↵ С:\ >dir ↵
Повторили пункты 15, 16 для директории t1.
С:\ >cd t1 ↵ С:\ >del *.* ↵ С:\ >dir ↵ С:\ >cd.. ↵
С:\ >rd t1 ↵ С:\ >dir ↵
Удалили файл из директории prim. Удалили саму директорию prim.
Проверили что удаление произошло.
С:\ >del *.* С:\ >cd.. С:\ >rd prim ↵ С:\ >dir ↵
Пример выполнения команд:

5.

Практическая часть
Для Linux
Команды Linux для управления файлами:
1.LS
Утилита для просмотра содержимого каталогов. По умолчанию показывает текущий каталог. Если в параметрах указать путь,
то она перечислит содержимое конечного каталога.
2.CAT
Печатает содержимое файла, переданного в параметре в стандартный вывод . Если передать несколько файлов, команда склеит
их.
3.CD
Позволяет перейти из текущего каталога в указанный. Если запустить без параметров – возвращает в домашний каталог.
4.PWD
Печатает текущий каталог. Это может быть полезно, если ваша командная строка Linux не выводит такую информацию.
5.MKDIR
Создание новых каталогов
6.FILE
Данная команда показывает тип файла.
7.CP
Копирование файлов и каталогов.
8.MV
Перемещение и переименование файлов и каталогов. В Linux это одна и та же операция. Переименование – это перемещение
файла в ту же папку с другим названием.
9.RM
Удаляет файлы и папки
10.LN
Создает жесткие или символические ссылки на файлы

6.

Практическая часть
Для Linux
11.CHMOD
Изменяет права доступа к файлу. Это чтение, запись и выполнение.
12.CHOWN
Изменяет владельца файла. Только суперпользователь может изменять владельцев
13.FIND
Поиск в файловой системе, файлах и папках.
14.SORT
Сортировка строк текста по различным критериям. Наиболее полезные опции: -n, по числовому значению, и –r,которая
переворачивает вывод.
15.WC
Утилита командной строки для подсчёта количества слов, строк, байт и символов.
Пример выполнения команд:

7.

Итог
В ходе лабораторной работы мы изучили составные части MS DOS и
операционной системы Linux, архитектуру, внутренние команды.
Применение на практике команды MS DOS. Изучили команды
создания удаления файлов, их копирования, изменили формат файла.
Изучили команды для перехода между директориями, их удаление.

8.

Лабораторная работа 2
Open MP. Обратная матрица. Метод
алгебраических дополнений, метод Гаусса, метод
Крамера
Цель: Знакомство
с технологией OpenMP. Изучение метода
алгебраических дополнений, метода Гаусса и метода Крамера. Практичекое
нахождение обратной матрицы.
Теория:
OpenMP — открытый стандарт для распараллеливания программ на
языках С, С++ и Фортран. Даёт описание совокупности директив
компилятора, библиотечных процедур и переменных окружения, которые
предназначены для программирования многопоточных приложений на
многопроцессорных системах с общей памятью.

9.

Практическая часть
Нахождение обратной матрицы для матрицы
размера 3 на 3 методом алгебраических дополнений
Алгебраическим
дополнением некоторого
элемента
определителя
называется минор этого
элемента, умноженный на
(-1)^S , где S - сумма
номеров
строки
и
столбца, на пересечении
которых стоит данный
элемент.

10.

Практическая часть
Нахождение обратной матрицы для матрицы
размера 3 на 3 методом Гаусса
Метод Гаусса – это метод решение квадратных систем линейных алгебраических
уравнений (СЛАУ), суть которого заключается в последовательном исключение
неизвестных переменных с помощью элементарных преобразований строк.

11.

Практическая часть
Нахождение обратной матрицы для матрицы
размера 3 на 3 методом Крамера
Метод Крамера — способ решения
систем линейных алгебраических
уравнений с числом уравнений равным
числу неизвестных с ненулевым
главным
определителем
матрицы
коэффициентов системы.

12.

Практическая часть
Код программы для нахождения детерминанта и
обратной матрицы

13.

Практическая часть
Тестирование программы
Так мы получили обратную матрицу для нашей матрицы 3 на 3

14.

Практическая часть
Текст программы для перемножения матриц

15.

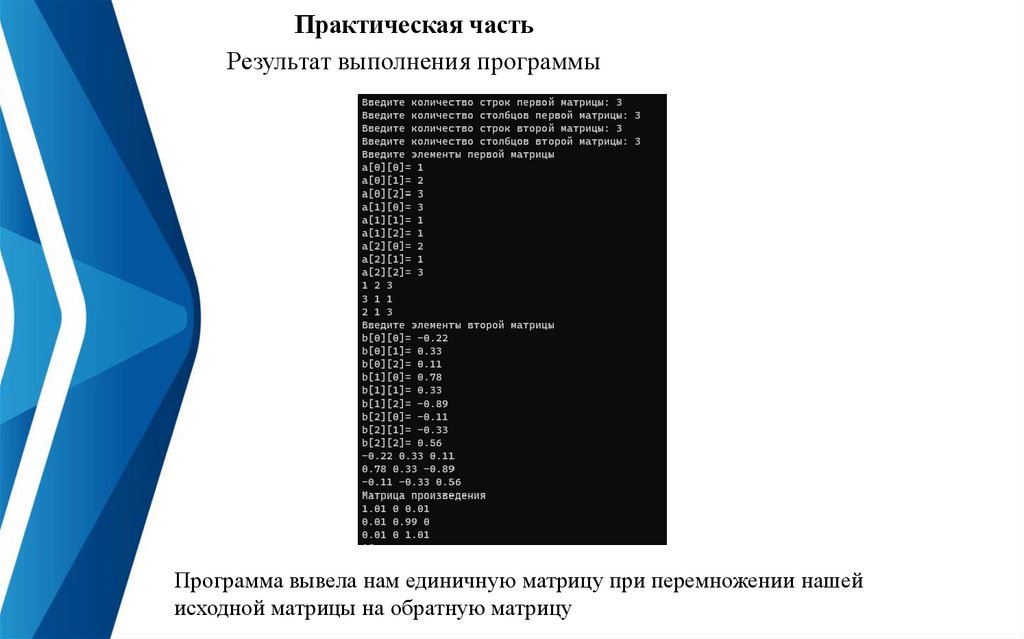
Практическая часть
Результат выполнения программы
Программа вывела нам единичную матрицу при перемножении нашей
исходной матрицы на обратную матрицу

16.

Итог
В ходе лабораторной работы мы изучили три метода нахождения
обратной матрицы и применили их на практике. Ознакомились со
стандартом OpenMP, написали программы на языке C++ для получения
обратной матрицы и перемножения двух матриц с целью получить
единичную матрицу, тем самым проверили правильность решения.

17.

Лабораторная работа 3
Метод наименьших квадратов при решении
переопределённых систем СЛАУ
Цель: Изучение способа решения систем линейных алгебраических
уравнений методом наименьших квадратов. Написание кода программ для
вычисления произведения и нахождение обратной матрицы. Проверка
соответствия эмпирических и программных вычислений.
Теория: Суть метода наименьших квадратов заключается в том, чтобы найти
такой вектор x, который минимизирует среднеквадратическую ошибку между
левой и правой частью уравнения. Для этого необходимо построить матрицу А и
вектор b, такие что Аx=b, и найти такой вектор x, который минимизирует ||Axb||^2.
Решение МНК-методом определяется следующим образом:
1.Составляется матрица A и вектор b для данной СЛАУ.
2.Вычисляется псевдообратная матрица A^-1, используя формулу: A^-1 =
(A^T*A)^-1 * A^T, где A^T – транспонированная матрица A.
3.Решение x определяется как x = A^-1 * b.
Задание: Решить систему из 4 уравнений с тремя неизвестными методом
наименьших квадратов.

18.

Практическая часть
Результат выполнения программы
Таким образом с помощью метода наименьших квадратов мы решили систему
уравнений

19.

Практическая часть
Решение системы уравнений с помощью программы
на С++
На данном этапе мы получаем
транспонированную матрицу А,
далее эту матрицу перемножаем на
исходную матрицу и получаем
матрицу С

20.

Практическая часть
Решение системы уравнений с помощью программы
на С++
Сейчас обратную матрицу С перемножаем на матрицу В и получаем наши
примерные корни x, y и z. Ответы совпали.

21.

Итог
В ходе лабораторной работы мы изучили способы решения систем
линейных алгебраических уравнений методом наименьших квадратов.
Написали коды программ для вычисления произведения и нахождение
обратной матрицы. Проверили соответствие эмпирических и
программных вычислений.

22.

Лабораторная работа 4
Программирование на Open MP. Вычисление
кратных интегралов
Цель: Изучение функций распараллеливания OpenMP, ее последовательных и
параллельных областей. Вычисление кратных интегралов, исследование
времени выполнения программы.
Теория: Вычисление кратных интегралов представляет значительную трудность
по сравнению с обычными интегралами.
1 трудность: для сохранения точности нужно вычислить большое количество
точек на интервале.
2 трудность: область интеграла имеет сложную формулу. Как правильно их
вычисляют в лоб.
Задание: Решить два кратных интеграла с помощью программ на языке С,
используя библиотеку omp.

23.

Практическая часть
Код программы для решения кратных интегралов

24.

Практическая часть
Результат выполнения программы
Для интеграла функции е^-(x^2+y^2)
Для интеграла функции - х^2 - y^2
Входные параметры для обоих интегралов

25.

Итог
В
ходе
лабораторной
работы
мы
изучили
функции
распараллеливания OpenMP ее последовательных и параллельных
областей. Вычислили сложную функцию методом многократных
интегралов от нее, исследовали время ее выполнения.

26.

Лабораторная работа 5
Метод Монте-Карло в параллельных
вычислениях. Закон Амдала
Цель: Изучение метода Монте-Карло и Закона Амдала. Применение его в параллельных
вычислениях.
Теория: Метод Монте-Карло – это численный метод, основанный на воспроизведении
большого числа реализаций случайного процесса, специально построенного по условиям
задачи. Суть метода заключается в следующем: процесс описывается математической
моделью с использованием генератора случайных величин, модель многократно
обсчитывается, на основе полученных данных вычисляются вероятностные характеристики
рассматриваемого процесса.
Закон Амдала:
В любой параллельной программе есть последовательная часть, которая образована
операциями ввода/вывода, синхронизации и т. д. Предположим, что по сравнению с
последовательным способом решения:
1)При разделении задачи на независимые подзадачи временные затраты на
межпроцессорное взаимодействие и объединение результатов пренебрежимо малы;
2)Время работы параллельной части программы уменьшается пропорционально числу
вычислительных узлов.
Задание: вычислить значение Pi с разной точностью, вычислить сколько процессоров
потребуется для решения задачи с разными входными данными, используя библиотеку
iomanip.

27.

Практическая часть
Код программы для вывода числа Pi с разной
точностью

28.

Практическая часть
Результат выполнения программы
С клавиатуры выводим
до какого знака нам
нужно вывести
дробную часть числа
Pi.

29.

Практическая часть
Код программы для подсчета стоимости вычислений

30.

Практическая часть
Результат выполнения программы
Первые входные данные:
Вторые входные данные:
Результат:
Результат:
Третьи входные данные:
Результат:
Таким образом можно сделать вывод, что на вторых входных
данных потребуется меньше всего процессоров для вычисления.

31.

Итог
В ходе лабораторной работы мы изучили метод Монте-Карло. А
также написали код для решения задачи по нахождению числа
процессоров с использованием закона Амдала.

32.

Лабораторная работа 6
Технология MPI. Запуск сообщений. Трансляция,
редактирование, выполнение программ
Цель: Изучение программного интерфейса MPI, его общих процедур.
Теория: Технология MPI - Message Passing Interface (MPI, интерфейс передачи
сообщений) — программный интерфейс (API) для передачи информации, который
позволяет обмениваться сообщениями между процессами, выполняющими одну задачу.
Наиболее распространённой технологией программирования для параллельных
кoмпьютepoв c pacпpeдeлeннoй памятью в настоящее время является MPI.
Ocнoвным способом взаимодействия параллельных процессов в таких системах является
передача сообщений друг другу. Это и отражено в названии данной технологии — Message
Passing Interface (интерфейс передачи сообщений). Стандарт MPI фиксирует интерфейс,
который должен соблюдаться как системой программирования на каждой вычислительной
платформе, так и пользователем при создании своих программ. Современные реализации,
чаще всего, соответствуют стандарту MPI версии 1.1. В 1997— 1998 годах появился
стандарт MPI-2.0, значительно расширивший функциональность предыдущей версии.
Задание: получить сообщение от пользователя используя встроенные функции библиотеки
MPI на языке С, вывести ряд простых чисел.

33.

Практическая часть
Код программы для отправки сообщения

34.

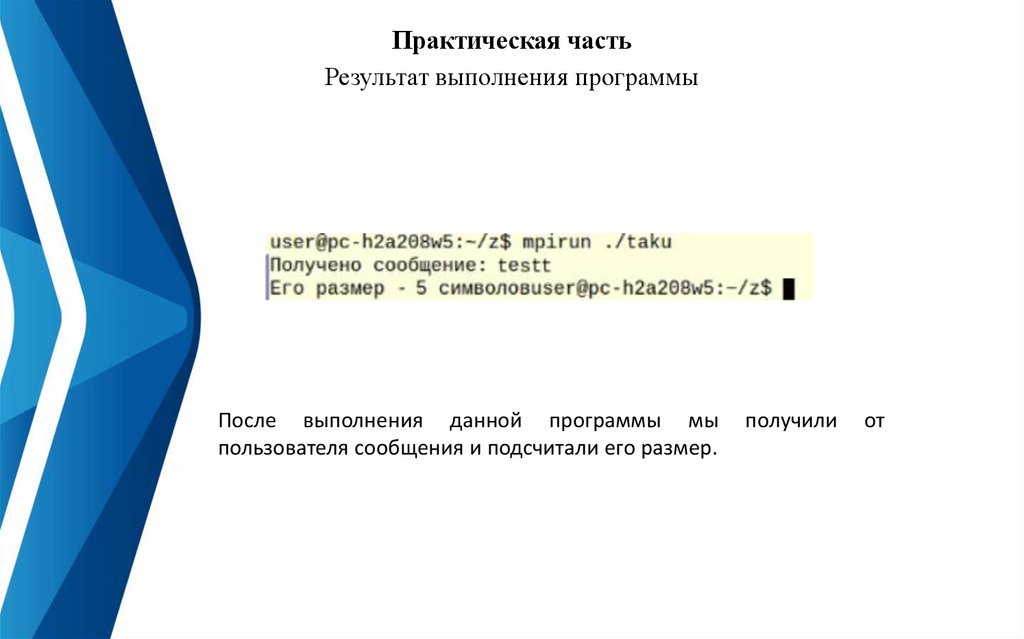
Практическая часть
Результат выполнения программы
После выполнения данной программы мы
пользователя сообщения и подсчитали его размер.
получили
от

35.

Практическая часть
Код программы для перестановки сообщений

36.

Практическая часть
Код программы для вывода последовательности
простых чисел заданной длины

37.

Практическая часть
Код программы для вывода последовательности
простых чисел заданной длины

38.

Практическая часть
Код программы для вывода последовательности
простых чисел заданной длины

39.

Практическая часть
Результат выполнения программы
В коде программы мы задали диапазон значений от 0 до 100 для
простых чисел и получили следующую последовательность

40.

Итог
В ходе лабораторной работы мы изучили программный интерфейс
MPI, его общие процедуры. Написали программы для получения и
перестановки сообщений и вывода последовательности простых
чисел.

41.

Лабораторная работа 7
Среда MPI – reduce. Поиск в массиве
максимального числа и его позиции. Сортировки
Цель: Вычисление индекса и значения максимального числа из файла, с использованием
технологии MPI. Выяснить, какая сортировка является наиболее эффективной.
Теория: Компиляция и запуск параллельной программы в среде MPI. Важнейшие
функции MPI.
Поскольку MPI является библиотекой, то при компиляции программы необходимо
прилинковать соответствующие библиотечные модули. Этo можно сделать в командной
строке или воспользоваться предусмотренными в большинстве систем командами или
скриптами mpicc (для программ на языке Си), mpiCC (для программ на языке Си++), и
mpif77/mpif90 (для программ на языках Фортран 77/90).
Опция компилятора "-o name" позволяет задать имя (name) для пoлyчaeмoгo выполнимого
фaйла, пo умолчанию выполнимый файл называется a.out.
Задание: Написать программу для вывода индекса и значения максимального числа из
файла. Сравнить три сортировки и выяснить какая из них эффективнее.

42.

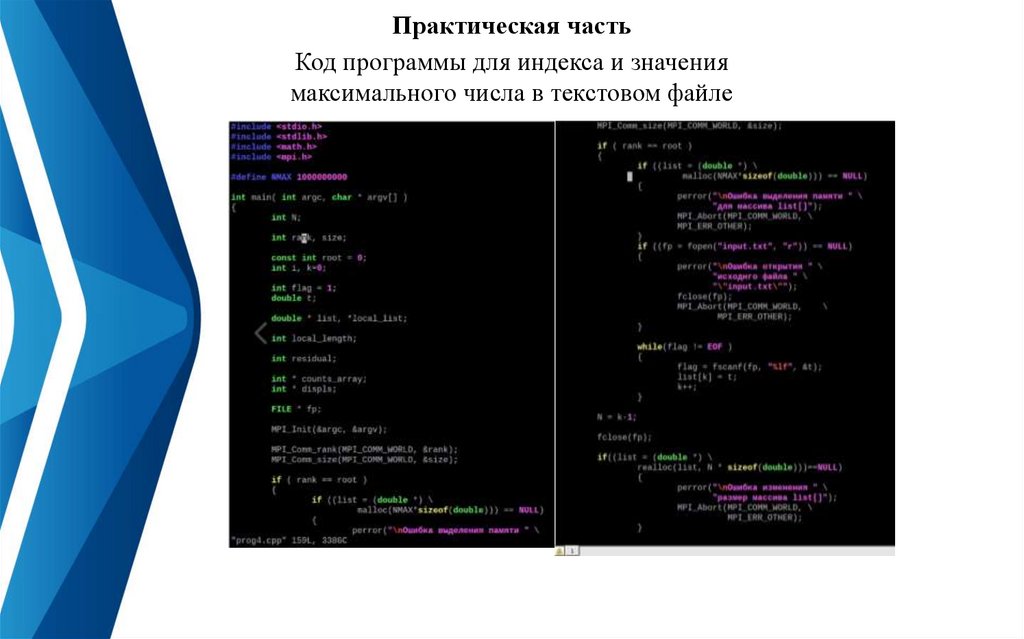
Практическая часть
Код программы для индекса и значения
максимального числа в текстовом файле

43.

Практическая часть
Код программы для индекса и значения
максимального числа в текстовом файле

44.

Практическая часть
Код программы для индекса и значения
максимального числа в текстовом файле

45.

Практическая часть
Результат выполнения программы
Входные данные:
После выполнения программы в консоль вывелось значение
наибольшего числа в массиве, а также его индекс.

46.

Практическая часть
Код программы для сортировки чисел слиянием

47.

Практическая часть
Код программы для сортировки чисел слиянием

48.

Практическая часть
Код программы для сортировки чисел пузырьком

49.

Практическая часть
Код программы для сортировки чисел сортировкой Шелла

50.

Практическая часть
Код программы для сортировки чисел сортировкой Шелла

51.

Практическая часть
Результат выполнения программы
Время выполнения сортировки слияния:
Время выполнения сортировки слияния:
Время выполнения сортировки слияния:
Самой эффективной сортировкой является сортировка Шелла, так как она
выполняется быстрее всего. Самой неэффективной является пузырьковая
сортировка.

52.

Итог
В ходе работы мы познакомились с средой MPI, с помощью нее
реализовали алгоритм для нахождения значения и индекса
максимального числа в последовательности, а также проверили
эффективность некоторых сортировок и выяснили какая из них
самая эффективная.