Методология построения и исследования имитационной модели. Теме 11

1.

Теме 11.
Методология построения и исследования
имитационной модели
Лекция
Принципы построения имитационных
моделей.
Способы имитации сложной системы.
Этапы математического моделирования

2.

УЧЕБНЫЕ ВОПРОСЫ:
1.Принципы формирования модельного
времени.
2. Способы имитации сложной системы.
3. Этапы
математического
вания ИМ
моделиро-

3.

Вопрос 1.
Принципы формирования модельного
времени

4.

При разработке имитационной модели
(ИМ)
сложной
системы
необходимо
учитывать следующие особенности.
1. Элементы
сложной
системы
функционируют
одновременно,
однако
параллельное
выполнение
нескольких
программ, имитирующих их поведение, в
ЭВМ трудноосуществимо или невозможно.

5.

2. Имитационная
модель
–
совокупность
программ
для
оперирующих
конечным
множеством
имитирующих
поведение
данных
и
ЭВМ,
системы не во все, а лишь в некоторые
моменты
времени
моделирования [0;Т].
из
интервала

6.

Для
имитации
параллельных
(одновременных) событий системы на
конечном множестве моментов времени в
имитационной
модели
используется
специальная
переменная,
называемая
модельным временем.

7.

Модельное время следует отличать от
других типов времени:
реального времени системы, функционирование которой имитируется;
машинного времени имитации, отража-
ющего затраты ресурса времени ЭВМ на
реализацию процесса моделирования.

8.

Существует два способа формирования
конечного множества моментов модельного
времени, известные как:
принцип "∆t"
принцип "∆x".

9.

"Принцип ∆t" заключается в изменении
модельного
времени
с
фиксированным
шагом ∆t.
"Принцип ∆x" заключается в изменении
модельного времени при скачкообразном
изменении вектора состояний системы на
некоторую величину ∆x.

10.

Скачкообразные
системы
изменения
происходят
при
состояния
наступлении
различных "особых" событий:
поступление управляющих сигналов;
поступление внешних воздействий;
выдача выходных сигналов и т.п.

11.

Рассмотрим
особенности
принципов "∆t" и "∆х".
Пусть сложная система состоит из
N элементов, поведение которых
предполагается моделировать.

12.

Для
каждого
элемента
локальное модельное время: t
Поведение
интервала
i-го
элемента
моделирования
определим
i
0, T .
в
течение
определяется
некоторой последовательностью действий:
i
i
i
G g1 , g 2 , , g Mi
i 1, N
(1.1)

13.

Составляющие выражения (1.1):
G – все множество действий элементов,
составляющих систему;
Mi – число действий для i-го элемента.

14.

Из множества G можно выделить
подмножество действий, на выполнение
которых в ИМ требуется ненулевое
модельное время:
i
i
i
D d1 , d 2 , , d Li
(1.2)
i 1, N
где Li – число действий с ненулевым
модельным временем.

15.

i
Для выполнения действия d j тре i
буется затратить модельное время j ,
где i 1, N ; j 1, Li .
–
i
Последовательность времен j
это случайные величины с заданными
законами распределения.

16.

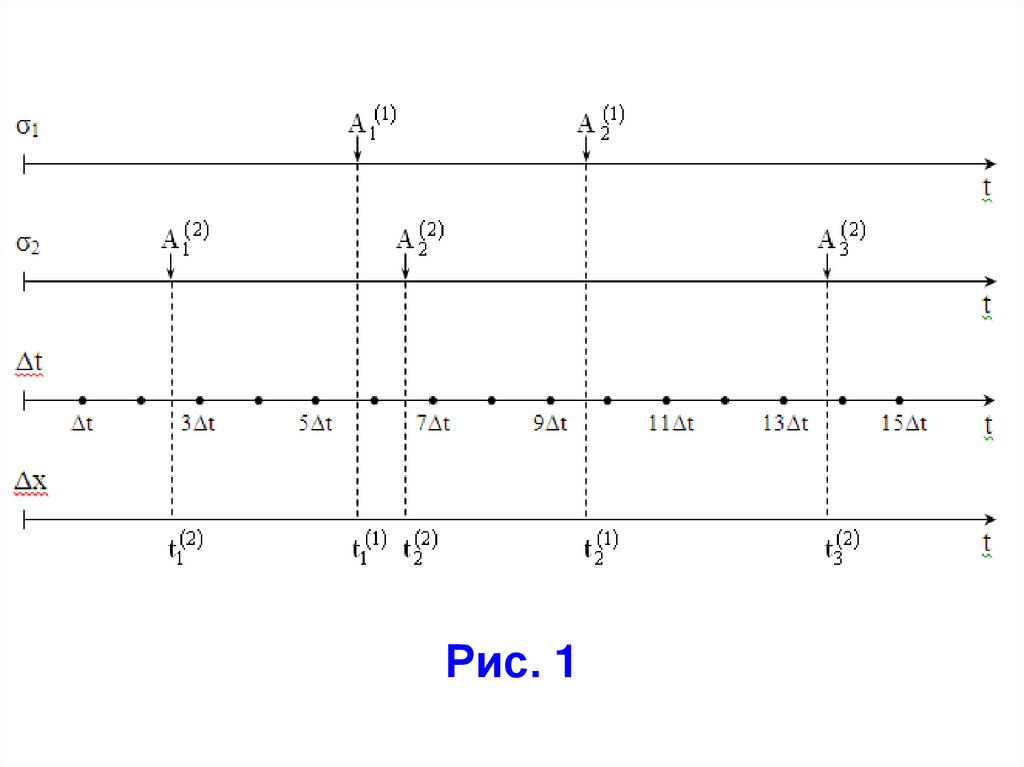
Рассмотрим реализацию принципов "∆t" и
"∆x" на примере системы, состоящей из 2-х
элементов σ1 и σ2 (рис. 1).

17.

Рис. 1

18.

Реализация "принципа Δt".
Разобьем временную ось на равные
дискреты ∆t.
В результате в процессе моделирования
время примет следующие значения:
{0, ∆t, 2∆t, …, 15∆t}.

19.

За событиями, попадающими в интервал
постоянства модельного времени закрепляется один и тот же момент времени.
На рис. 1 события и соответствующие им
значения модельного времени наступают в
следующем порядке:
(1.3)

20.

При этом фазовая траектория имеет
следующие составляющие:
(1.4)

21.

Недостатки "принципа ∆t":
1) если
∆t
достаточно
мало,
то
выполняется много лишних вычислений, и
возрастает
имитацию;
время,
затрачиваемое
на

22.

2) даже
наступления
при
малом
реальных
∆t
моменты
событий
могут
несовпадать с их аналогами в ИМ, т.е.
модель будет искажать реальную фазовую
траекторию системы.

23.

Реализация "принципа ∆x".
В соответствии с ним изменение
модельного времени происходит в моменты
наступления особых событий, и фазовая
траектория для рис. 1 будет иметь вид:
(1.5)

24.

Принцип ∆t используется в следующих
случаях:
i
1) события A j наступают через равные
промежутки времени;
2) событий происходит
появляются группами.
много
и
они
В остальных случаях более экономичным
и точным является принцип ∆х.

25.

Вопрос 2.
Способы имитации сложной системы
Способ имитации сложной системы –
это способ формирования ее фазовой
траектории.

26.

Выделяют
три
способа
имитации
сложной системы:
1) событийный – основан на фиксирова i
нии моментов наступления событий A j ;

27.

2) просмотр активностей – основан на
результатах
i
анализа
действий d j ,
на
осуществление которых требуются затраты
i
модельного времени j .
При этом пара
d , называется (i,ј)-й
i
i
j
j
активностью системы;

28.

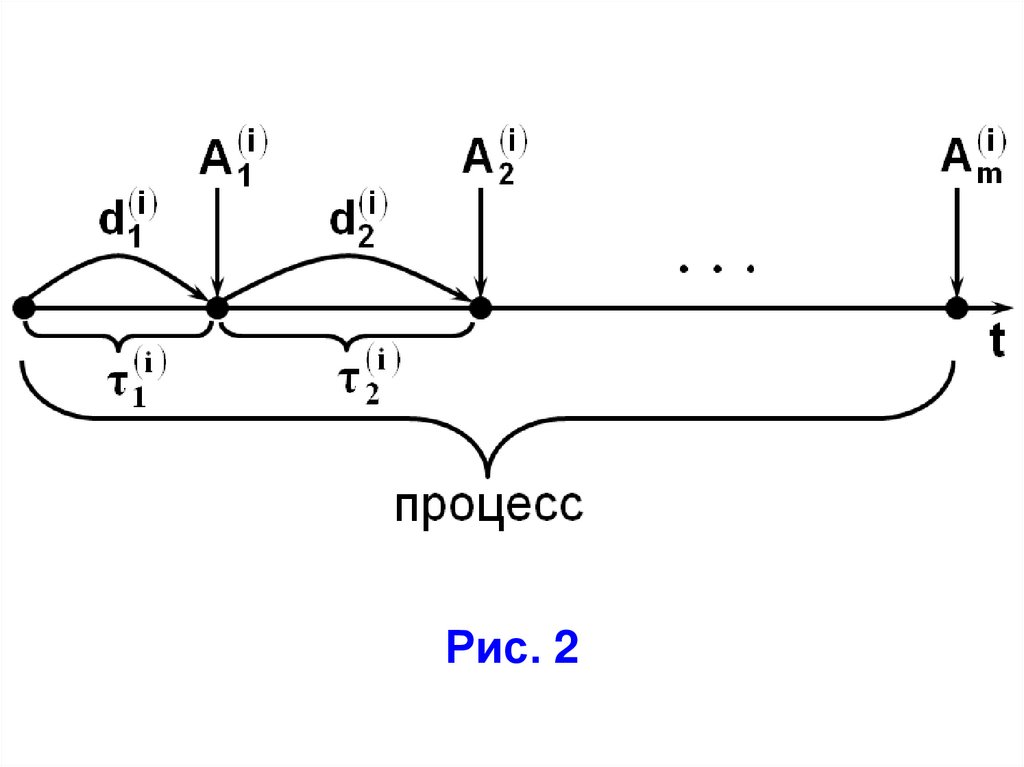
3) процессный – основан на выполнении
хронологической
последовательности
событий
и
действий,
называемой
процессом.
На базе процессного сформировался
транзактный
способ
имитации
для
моделирования СМО.
Взаимосвязь
между
понятиями
"событие", "действие", "процесс" представлена на рис. 2.

29.

Рис. 2

30.

Условия применения способов имитации.
Событийный способ:
1) множество
особых
событий
можно
сгруппировать по типам;
2) для каждого типа событий определена
последовательность действий, приводящая
к изменению состояния системы;

31.

3) определены
условия
перехода
от
одного типа события к другому;
4) интервалы времени между наступлениями событий – случайные величины с
известными законами распределения.

32.

Способ,
основанный
на
просмотре
каждого
элемента
активностей:
1) действия
системы
для
различны
и
приводят
к
наступлению различных событий;
2) каждое
действие
характеризуется
набором условий его выполнения;

33.

3) времена
выполнения
действий
являются случайными величинами с извест-
ными законами распределения.

34.

Процессный способ.
Этот способ сочетает в себе черты
первых двух.
Применяется, когда поведение элементов
системы может быть описано фиксирован-
ными последовательностями событий и
действий, называемых процессами.

35.

Вопрос 3.
Этапы имитационного моделирования

36.

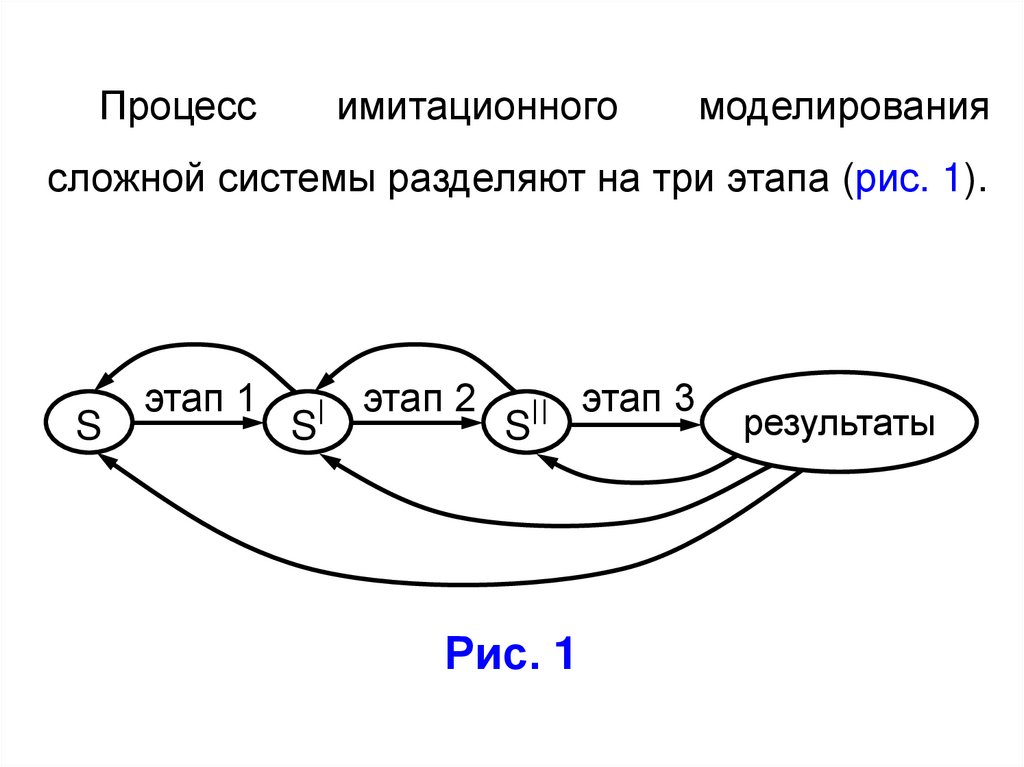
Процесс
имитационного
моделирования
сложной системы разделяют на три этапа (рис. 1).
S
этап 1
|
S
этап 2
||
S
Рис. 1
этап 3
результаты

37.

Обозначения на рис. 1:
S – исследуемая сложная система;
|
S – концептуальная модель системы S;
||
S – имитационная модель системы S.
Концептуальная модель системы – ее
упрощенное математическое или алгоритмическое описание.

38.

Этап 1.
На данном этапе на основании изучения
и содержательного описания системы S
осуществляется переход к концептуальной
|
модели S .
Концептуальной
моделью
сложной
системы
называется
ее
упрощенное
математическое
или
алгоритмическое
описание.

39.

Этот этап включает следующие шаги:
1.1. постановка
исследования;
задачи
и
целей
1.2. анализ системы, т.е. декомпозиция
ее на отдельные элементы для удобства
математического описания;
1.3. определение параметров, переменных и пространства состояний системы;
1.4. выбор показателей эффективности;
|
1.5. описание концептуальной модели S
системы S и проверка ее адекватности.

40.

Этап 2.
На
данном
этапе
осуществляется
|
переход от концептуальной модели S к
моделирующему алгоритму и имитационной
||
модели S .

41.

Этот этап включает следующие шаги:
2.1. выбор
способа
имитации
и
программных средств реализации ИМ;
2.2. построение
моделирующего
алгоритма;
2.3. алгоритмизация
математических
моделей, описывающих поведение всех
элементов системы;
2.4. разработка ИМ, т.е. программирование
моделирующего алгоритма;
2.5. отладка, тестирование и проверка
адекватности имитационной модели.

42.

Этап 3.
На
данном
этапе
осуществляется
исследование системы S с помощью ее
||
имитационной модели S , т.е. проведение
имитационных экспериментов, анализ и
обобщение результатов моделирования.

43.

Этот этап включает три шага.
3.1. Планирование
эксперимента
–
процесс
имитационного
задания
всех
значений параметров системы, используемых при моделировании.
Выбор
этих
значений
определяется
целью имитационного эксперимента.

44.

3.2. Прогон
имитационной
имитационный
эксперимент
модели
с
–
моделью
||
системы S , в результате которого для
заданных значений параметров системы
имитируется
ее
вычисляются
показатели
(ПЭ).
фазовая
траектория
и
эффективности

45.

В результате одного прогона
получают случайные значения ПЭ.
ИМ
По одной случайной реализации ПЭ
нельзя
судить
об
эффективности
функционирования системы.
Поэтому
на
данном
этапе
осуществляется несколько прогонов ИМ, в
результате которых получается случайная
выборка значений ПЭ.

46.

3.3. Обработка, анализ и интерпретация
результатов моделирования.
Этот
шаг
реализуется
для
оценки
эффективности функционирования системы
S по случайной выборке значений ПЭ.