Основные уравнения математической физики. Уравнения эллиптического типа (лекция 13)

1.

Математическое
моделирование
физических систем
Лекция 13. Основные
уравнения
математической физики.
Уравнения
эллиптического типа

2.

Эллиптические (стационарные процессы)
2u 2u 2u
2 2 f
2
x
y
z
• Канонический вид
• Уравнение
• Пуассона
• (Лапласса)
u u u
g g g f
x x y y z z
При постановке задач для ДУ в частных производных обычно требуется найти
распределение , удовлетворяющее ДУ в некоторой области пространства с границей Г.
y
Г
x

3.

Уравнения эллиптического типа
Закон сохранения массы жидкости в выделенном объеме V
С силу произвольного выбора объема V подынтегральная
функция должна быть тождественна равна нулю и следует
уравнение неразрывности сплошной среды:
3

4.

Дивергенция векторного поля
• Характеризует распределение в пространстве
источников векторного поля
• Например, источниками электрического поля
являются заряды, положительные или
отрицательные.
• В этом случае
дает
распределение зарядов.
4

5.

Уравнения эллиптического типа
Рассмотрим установившееся
течение жидкости, для которого ее
скорость не зависит от времени:
5

6.

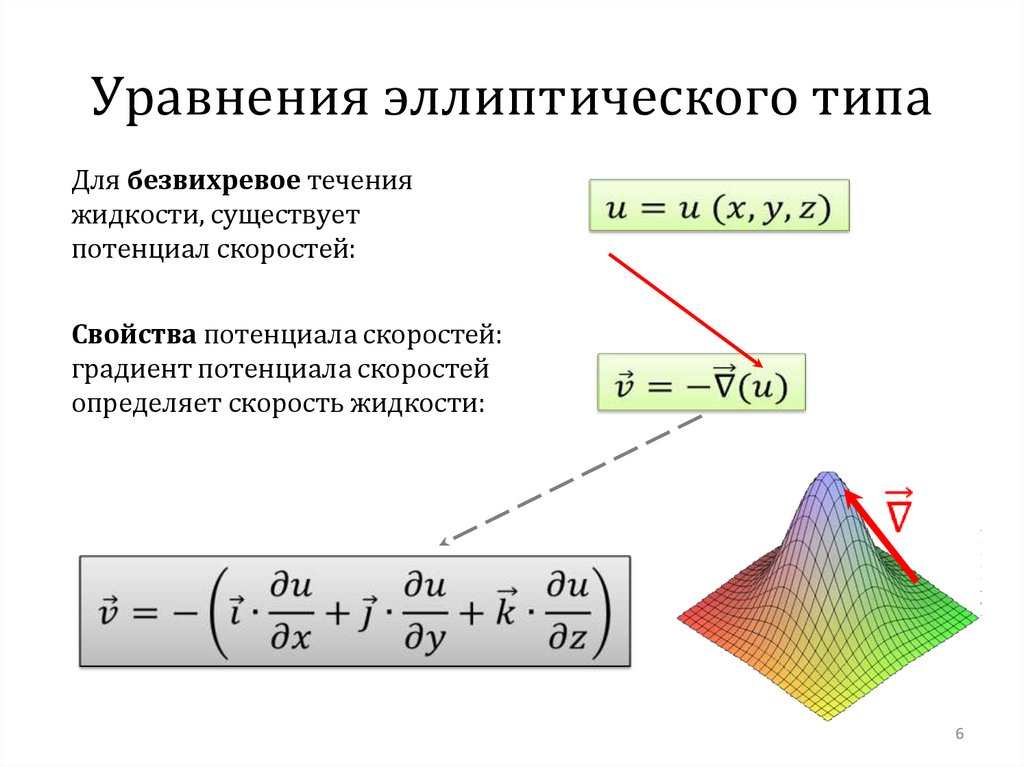
Уравнения эллиптического типа
Для безвихревое течения
жидкости, существует
потенциал скоростей:
Свойства потенциала скоростей:
градиент потенциала скоростей
определяет скорость жидкости:
6

7.

Уравнения эллиптического типа
Для потенциала скоростей,
справедливо уравнение Лапласа:
Laplace, Pierre-Simon
(1749–1827), французский
математик, физик и
астроном
или
здесь
оператор Лапласа
Уравнение Лапласа возникает во многих
физических задачах механики,
теплопроводности, электростатики, гидравлики,
квантовой физике, в частности в уравнении
Шрёдингера.
7

8.

Уравнения эллиптического типа
Johann Carl Friedrich Gauß;
1777-1855, Гёттинген):
немецкий математик,
механик, физик, астроном
и геодезист.
8

9.

Уравнения эллиптического типа
С помощью теоремы
Остроградского-Гаусса
преобразуем последнее
выражение к дифференциальной
форме:
или
9

10.

Уравнения эллиптического типа
В силу произвольного
выбора объема V
подынтегральная функция
должна быть тождественна
нулю!
Связь электрического
поля и
электростатического
потенциала:
здесь
оператор Лапласа
10

11.

Уравнения эллиптического типа
Для электростатического потенциала
справедливо уравнение Пуассона:
Siméon Denis Poisson
(1781-1840, Франция),
французский математик,
механик и физик.
В декартовой системе координат:
Уравнение Пуассона описывает:
• электростатическое поле,
• стационарное поле температуры,
• поле давления,
• поле потенциала скорости в гидродинамике.
11

12.

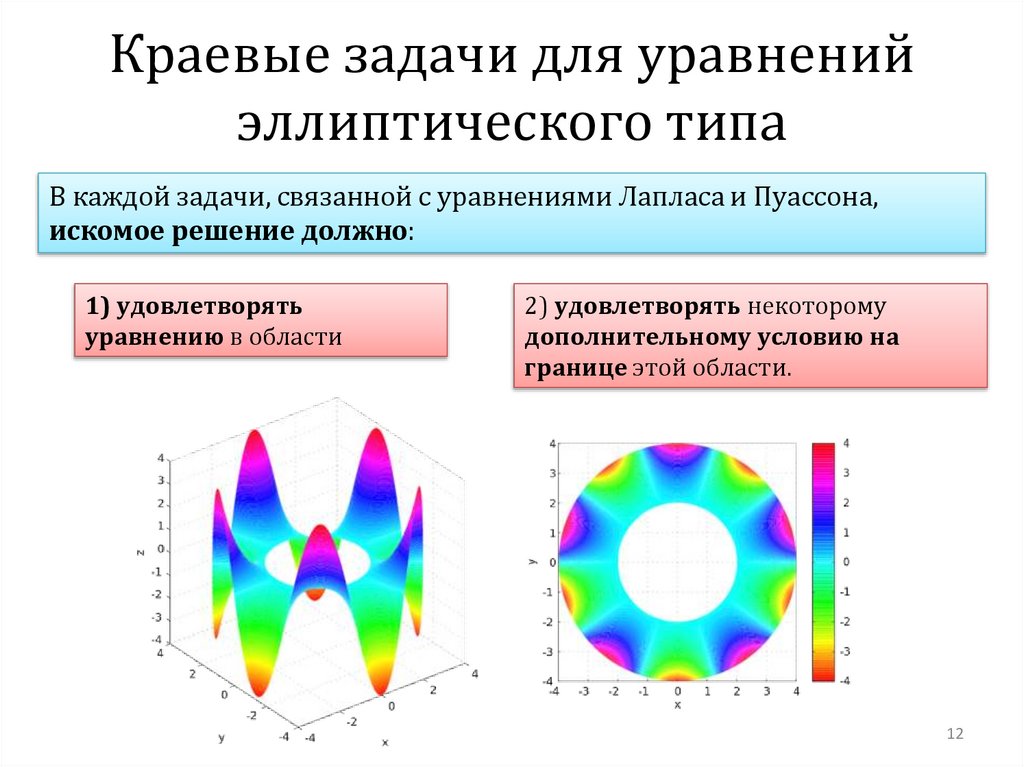
Краевые задачи для уравнений
эллиптического типа
В каждой задачи, связанной с уравнениями Лапласа и Пуассона,
искомое решение должно:
1) удовлетворять
уравнению в области
2) удовлетворять некоторому
дополнительному условию на
границе этой области.
12

13.

Краевые задачи для уравнений
эллиптического типа
В зависимости от вида граничных условий различают следующие
виды граничных задач:
1) Задача Дирихле
13

14.

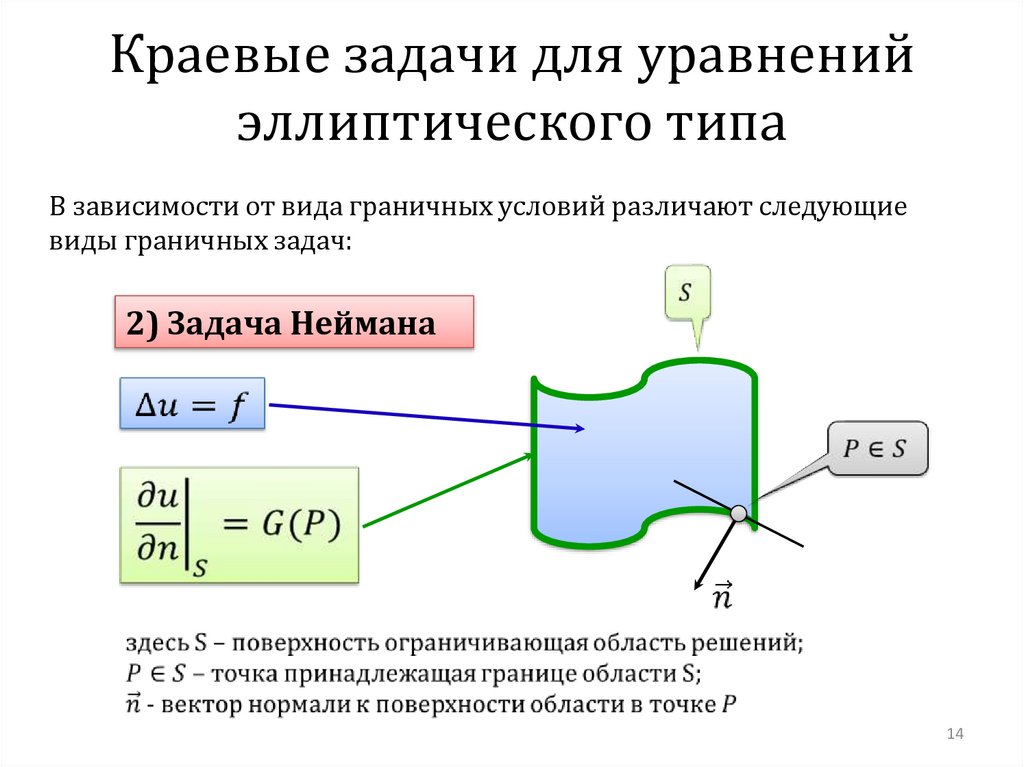
Краевые задачи для уравнений
эллиптического типа
В зависимости от вида граничных условий различают следующие
виды граничных задач:
2) Задача Неймана
14

15.

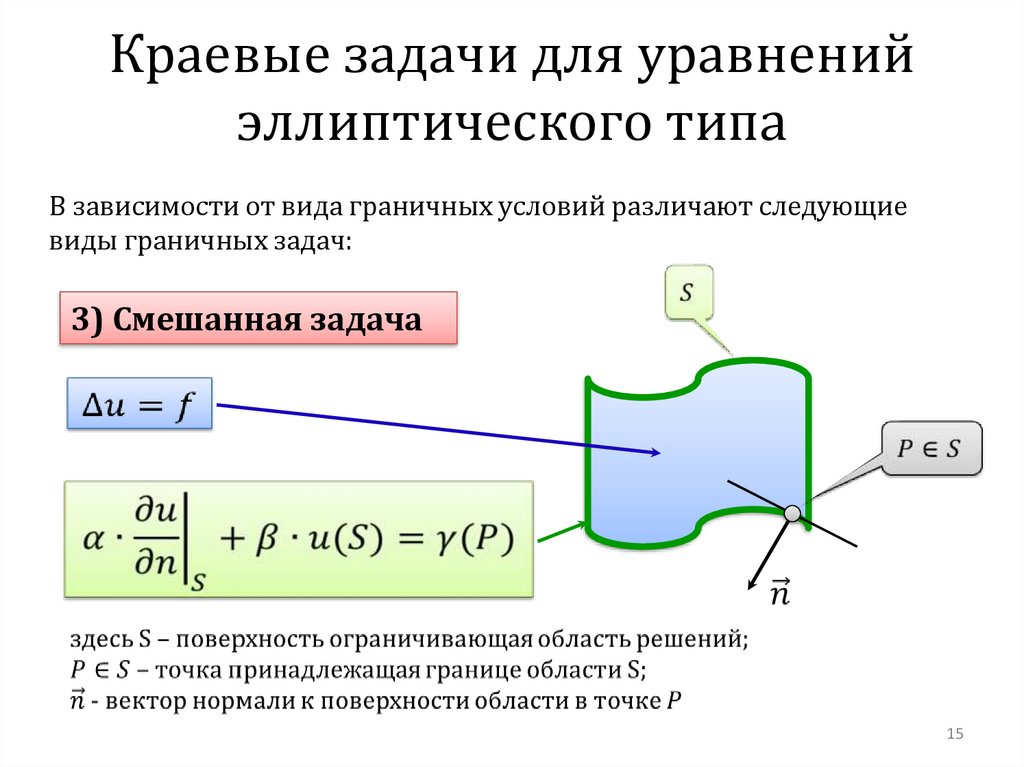
Краевые задачи для уравнений
эллиптического типа
В зависимости от вида граничных условий различают следующие
виды граничных задач:
3) Смешанная задача
15