Основы трансляции языков программирования. Лекции 4-5. Синтаксический анализ. Грамматики. Нисходящий синтаксический анализ

1.

ОСНОВЫ ТРАНСЛЯЦИИ
ЯЗЫКОВ ПРОГРАММИРОВАНИЯ
Лекции 4-5
Синтаксический анализ.
Грамматики.
Нисходящий синтаксический
анализ.
LL(1)-грамматики.
https://do.ssau.ru/moodle/course/view.php?id=1376

2.

Фазы трансляции
Препроцессор
Лексический анализ
Синтаксический анализ
Семантический анализ
Генерация кода
2/38

3.

Лексический анализ
Основные функции лексического анализа состоят в группировке
последовательностей знаков исходного кода в символы языка.
Пример. if Sum>5 then pr:= true;
Лексема
Лексемы
Служебные слова
Идентификаторы
Литералы
Служебные
символы
Тип
if
Служебное слово
Sum
Идентификатор
>
Служебный символ
5
Литерал
then
Служебное слово
pr
Идентификатор
:=
Служебный символ
true
Литерал
;
Служебный символ
Значение
Код «if»
Ссылка
Адрес в таблице идентификаторов
Код «>»
Адрес в таблице литералов
Код «then»
Адрес в таблице идентификаторов
Код «:=»
Адрес в таблице литералов
Код «;»
-
Несмотря на общую простоту процесса лексического анализа, существует небольшое количество языковых
характеристик, что усложняют создание лексических анализаторов.
Например:
Ключевые слова языка доступны для использования в качестве идентификаторов.
Интерпретация некоторых последовательностей знаков является
контекстно-зависимой.
3/38

4.

Синтаксический анализ
Структура программы
Основные функции синтаксического анализа состоят в группировке
лексем в элементы программы.
Пример. if Sum>5 then pr:= true;
Определение
данных
Лексема
if
Служебное слово
Описание
функций
Sum
Идентификатор
Оператор
Выражение
….
Тип
>
Служебный символ
5
Литерал
then
Служебное слово
pr
Идентификатор
:=
Служебный символ
true
Литерал
;
Служебный символ
Значение
Код «if»
Код «>»
Логическое
выражение
Условный
оператор
Код «then»
Код «:=»
Оператор
присваивания
Код «;»
Задача синтаксического анализа состоит в нахождении порождения
конкретного выражения с использованием данной грамматики.
Вида синтаксического анализа:
Нисходящий анализ – требуется найти левое порождение.
Восходящий анализ – требуется найти правое порождение.
4/38

5.

Синтаксический анализ
Синтаксический анализ является центральным элементом
транслятора.
синтаксис характеризует элементы, относящиеся к структуре программы:
описания и определения данных, функций, классов и других элементов
программы, операторы, выражения – это все синтаксические элементы разных
уровней.
вся программа представляет собой одно синтаксическое целое.
Задачей синтаксического анализа является построение структуры –
синтаксического дерева, отражающего взаимное расположение всех
синтаксических элементов программы (их порядка следования,
повторяемости, вложенности, приоритетов).
Средством описания синтаксиса являются формальные грамматики,
а их свойства используются для построения распознавателей,
базирующихся на табличном описании правил их поведения в
сочетании со стековой памятью (магазинные автоматы).
5/38

6.

Ограничения КА
Язык {xn yn | n 0}
невозможно определить посредством регулярного выражения,
поскольку в регулярных выражениях не существует возможности
указать, что количество элементов х должно равняться количеству
элементов у.
Значит невозможно построить конечный автомат.
Решение – использование продукций грамматик
S xSy
S xy
- читается как «имеет вид» или «может иметь вид»
S xSy xxSyy xxxyyy
Последовательность шагов,
использованная для генерации строки с применением продукций
грамматики, называется порождением строки.
- читается как «порождает»
6/38

7.

Грамматики
Грамматика определяется как следующая
четвёрка (VT ,VN , P, S )
VT — алфавит, символы которого называют терминальными символами, или терминалами.
VN — алфавит с нетерминальными символами, или нетерминалами.VT и VN
не имеют общих символов (т.е. VT VN )
V VT VN
Р — множество продукций (или правил), каждый элемент которого состоит
из пары α, β , где α — левая часть продукции, β — правая часть продукции,
а сама продукция записывается следующим образом : α β
α V (строки, состоящие из одного или более символов V );
β V * (строки, состоящие из нуля или более символов V );
S VN , называется символом предложения, или аксиомой грамматики,
и с него начинается генерация любой строки языка.
7/38

8.

Порождение строк
Рассмотрим язык {xn y n | n 0}
и грамматику G ({x, y},{S}, P, S )
P {S xSy, S xy}
Рассмотрим порождение строки
S xSy xxSyy xxxyyy
Каждая из строк, фигурирующих в порождении, называется
сентенциальной формой, а последняя строка (состоящая
только из терминалов) называется предложением языка.
Использование символа между двумя сентенциальными
формами обозначает, что строка справа от этого символа
получена из строки слева от него посредством одного
порождения.
Для сокращения можно записать
S * xxxyyy
8/38

9.

Эквивалентные грамматики
Для генерации конкретного языка обычно не существует единственной
грамматики. На тривиальном уровне любой нетерминал можно заменить ещё
неиспользованным символом. Можно произвести более значительные изменения –
изменить форму и количество продукций.
Грамматики:
P {S XY , X xX , X ε, Y yY , Y ε}
P {S xS , S yB, S x, S y, B yB, B y, S ε}
Определяют один и тот же язык:
{xn ym | n, m 0}
Две грамматики генерирующие один и тот же язык называются эквивалентными.
Иногда при создании компилятора оказывается полезным или даже необходимым
заменить данную грамматику эквивалентной.
9/38

10.

Иерархия грамматик
10/38

11.

Иерархия грамматик
Хомский определил четыре класса грамматик:
11/38

12.

Иерархия грамматик
Тип 0 или рекурсивно-перечислимые, определяются как все
грамматики, которые соответствуют данному выше
определению без ограничений на типы продукций.
◦ Грамматики 0-го типа эквивалентны машинам Тьюринга в том
смысле, что для любой данной грамматики 0-го типа существует
машина Тьюринга, которая допускает, и только допускает, все
предложения, сгенерированные данной грамматикой. И наоборот,
для данной машины Тьюринга существует грамматика 0-го типа,
которая генерирует точно все предложения, допускаемые машиной
Тьюринга.
Тип 1 или контекстно-зависимые. Определяются наложением
следующего ограничения на продукции грамматики Типа 1 :
для всех продукций вида α β выполняется условие, что α β
◦ Если обратиться к теории автоматов, грамматики 1-го типа
эквивалентны линейно ограниченным автоматам в том же смысле,
как грамматики 0-го типа эквивалентны машинам Тьюринга.
12/38

13.

Иерархия грамматик
Тип 2 или контекстно-свободная, КС-грамматика определяется
наложением следующего ограничения на грамматику 1-го типа:
в левой части продукции должен находиться только один
нетерминал
◦ Грамматики 2-го типа эквивалентны магазинным автоматам.
Тип 3 или регулярные грамматики – праволинейные или
леволинейные грамматики
Праволинейная грамматика – если в правой части продукции
грамматики присутствует нетерминал, то он должен находиться
только справа от терминала
Леволинейная грамматика - если в правой части продукции
грамматики присутствует нетерминал, то он должен находиться только
слева от терминала.
В грамматики Типа 2 и 3 типа полезно добавить продукцию вида
13/38
S ε

14.

Рекурсии в грамматиках
Грамматика с продукциями
P { A Ab; B cB; C dCf }
содержит прямые рекурсии, левую, правую и среднюю соответственно.
Грамматика с продукциями
P { A Bc; B Cd ; C Ae}
содержит непрямую рекурсию.
В тех немногих случаях, когда грамматика не содержит рекурсии, язык является
конечным, т.е. регулярным, поскольку можно просто перечислить все предложения
языка.
Любой конечный набор строк можно представить регулярной грамматикой.
Чрезвычайно полезным является утверждение (приводим без доказательства):
"Если грамматика не содержит средней рекурсии, то генерируемый ею язык является
регулярным".
Регулярные грамматики (3-го типа) почти всегда можно использовать в качестве основы
лексического анализа.
Контекстно-свободные грамматики (2-го типа), в основном, необходимы для
синтаксического анализа.
14/38

15.

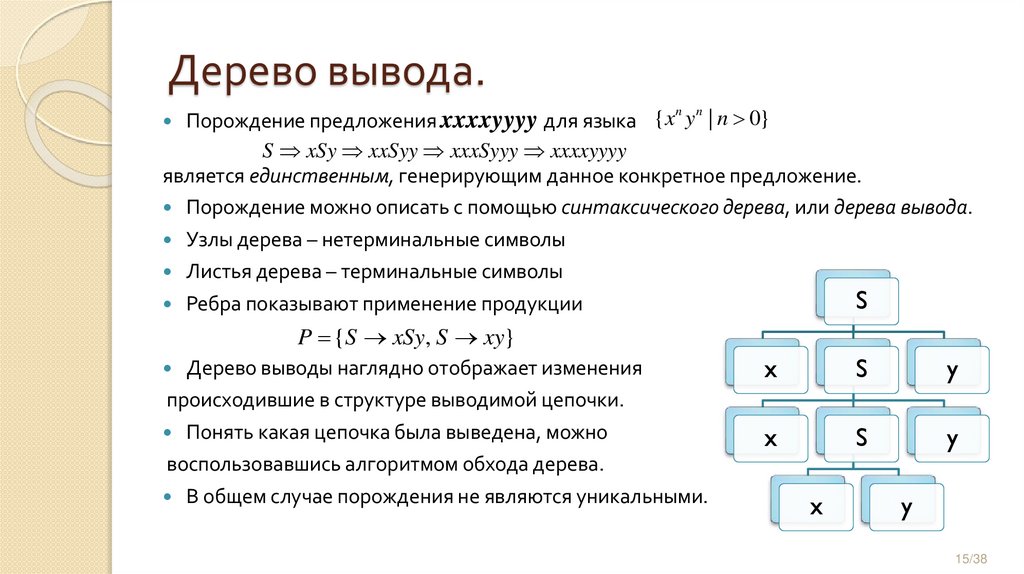
Дерево вывода.
Порождение предложения xxxxyyyy для языка {x y | n 0}
S xSy xxSyy xxxSyyy xxxxyyyy
является единственным, генерирующим данное конкретное предложение.
Порождение можно описать с помощью синтаксического дерева, или дерева вывода.
Узлы дерева – нетерминальные символы
Листья дерева – терминальные символы
S
Ребра показывают применение продукции
n
n
P {S xSy, S xy}
Дерево выводы наглядно отображает изменения
происходившие в структуре выводимой цепочки.
Понять какая цепочка была выведена, можно
воспользовавшись алгоритмом обхода дерева.
В общем случае порождения не являются уникальными.
x
S
y
x
S
y
x
y
15/38

16.

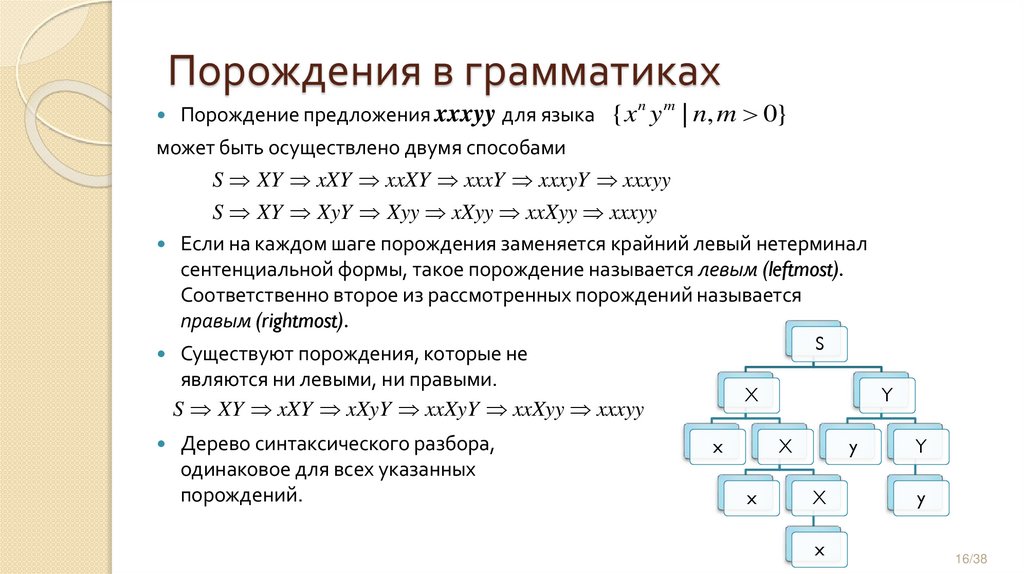
Порождения в грамматиках
Порождение предложения xxxyy для языка {x y | n, m 0}
n
m
может быть осуществлено двумя способами
S XY xXY xxXY xxxY xxxyY xxxyy
S XY XyY Xyy xXyy xxXyy xxxyy
Если на каждом шаге порождения заменяется крайний левый нетерминал
сентенциальной формы, такое порождение называется левым (leftmost).
Соответственно второе из рассмотренных порождений называется
правым (rightmost).
S
Существуют порождения, которые не
являются ни левыми, ни правыми.
S XY xXY xXyY xxXyY xxXyy xxxyy
Дерево синтаксического разбора,
одинаковое для всех указанных
порождений.
X
x
Y
X
x
y
X
x
Y
y
16/38

17.

Неоднозначность грамматик
Для многих грамматик любому предложению, которое можно
сгенерировать, соответствует единственное правое или левое
порождение.
◦ В регулярных грамматиках для каждой строки существует единственное
порождение. Это связано с тем, что в сентенциальной форме имеется не более
одного нетерминала.
Такие грамматики называются однозначными (unambiguous).
В противном случае грамматика является неоднозначной (ambiguous).
Если все грамматики, генерирующие язык, являются неоднозначными,
язык также называют неоднозначным
Пример: S S S
S x
S S S x S x S S x x S x x x
S S S S S S x S S x x S x x x
17/38

18.

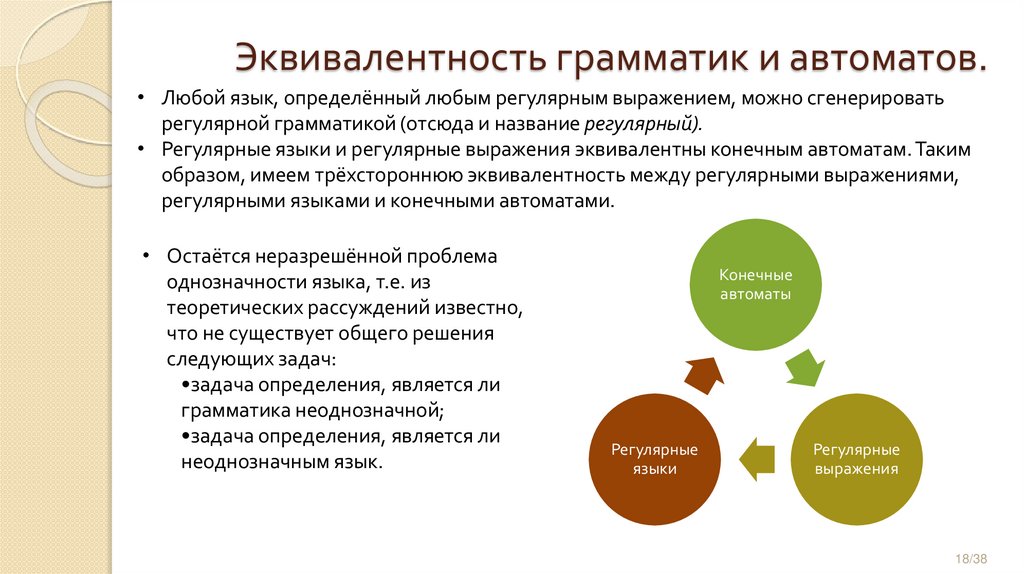
Эквивалентность грамматик и автоматов.
• Любой язык, определённый любым регулярным выражением, можно сгенерировать
регулярной грамматикой (отсюда и название регулярный).
• Регулярные языки и регулярные выражения эквивалентны конечным автоматам. Таким
образом, имеем трёхстороннюю эквивалентность между регулярными выражениями,
регулярными языками и конечными автоматами.
• Остаётся неразрешённой проблема
однозначности языка, т.е. из
теоретических рассуждений известно,
что не существует общего решения
следующих задач:
•задача определения, является ли
грамматика неоднозначной;
•задача определения, является ли
неоднозначным язык.
Конечные
автоматы
Регулярные
языки
Регулярные
выражения
18/38

19.

Грамматики и порождение строк
n n
Определим для языка {x y | n 0}
грамматику G ({x, y},{S}, P, S )
P {S xSy, S xy}
Рассмотрим порождение строки
S xSy xxSyy xxxyyy
Задача синтаксического анализа состоит в нахождении
порождения конкретного выражения с использованием
данной грамматики.
Виды синтаксического анализа:
Нисходящий анализ
– требуется найти левое порождение.
Восходящий анализ
– требуется найти правое порождение.
19/38

20.

Нисходящий синтаксический анализ
Принятие решений при нисходящем синтаксическом разборе,
основывается на символе (или последовательности символов)
предпросмотра.
По определению, символ предпросмотра (lookahead symbol) —
это либо текущий входной символ, либо маркер конца
(специальный символ, стоящий в конце строки) – ε.
На каждом этапе алгоритма первый незачёркнутый символ
входной строки определяется как входной символ и
используется для разбора.
Если в сентенциальной форме генерируется терминал,
появляется зачёркнутый символ.
20/38

21.

Критерий принятия решений
Для каждого нетерминала, который находится в левой части
нескольких продукций, необходимо найти такие непересекающиеся
множества символов предпросмотра, чтобы каждое множество
содержало символы, соответствующие точно одной возможной
правой части.
Объединение различных непересекающихся множеств для заданного
нетерминала не обязательно должно составлять алфавит, на котором
определён язык.
Выбор конкретной продукции для замены данного нетерминала
определятся символом предпросмотра и множеством, к которому
принадлежит данный символ.
Если символ предпросмотра не принадлежит ни одному из
непересекающихся множеств, можно сделать вывод о наличии
синтаксической ошибки.
21/38

22.

Множество символов предпросмотра
Множество символов предпросмотра, соотнесённых с применением
определённой продукции, называется её множеством первых порождаемых
символов.
Множество первых порождаемых символов продукции определяется как
множество всех терминалов, которые, выступая как символы предпросмотра,
указывают на использование данной продукции.
Стартовый символ данного нетерминала определяется как любой символ,
который может появиться в начале строки, генерируемой нетерминалом.
Символ-последователь данного нетерминала определяется как любой
символ, который может следовать за нетерминалом в любой сентенциальной
форме.
Таким образом:
множество первых порождаемых символов для продукции
A BC
будет включать все символы-последователи А,
а также стартовые символы ВС .
22/38

23.

Стартовые символы. Пример.
T aG {a}
T bG {b}
R BG
R CH
B cD
B TV
R BG {a, b, c}
Для R символ с очевидно является стартовым поскольку существует B→cD.
Поскольку B→TV и T→aG|bG то , значит {a,b} также являются стартовыми
для R.
23/38

24.

LL(k) – грамматики
КС – грамматика называется LL(k) – грамматикой если для заданной
цепочки языка ωAα и первых k символов выводящихся из Aα , существует не
более одного правила, которое можно применить к A, чтобы получить вывод
терминальной цепочки начинающейся с ω и продолжающейся k терминалами.
◦ первое L обозначает чтение слева направо,
◦ второе L обозначает использование левых порождений,
Пример:
S A B
A aAb 0
B aBbb 1
Определяет язык
a n 0b n a n1b 2 n , n 0
Грамматика не является LL(k) – грамматикой ни для какого k .
Интуитивно понятно, что встретив цепочку символов мы не знаем какое из двух правил
надо применять.
24/38

25.

LL(1) – грамматики
LL(1) – грамматику можно определить как
грамматику, в которой для каждого нетерминала,
появляющегося в левой части нескольких
продукций, множества первых порождаемых
символов всех продукций, в которых появляется этот
нетерминал, являются непересекающимися.
◦ k=1 – используем ровно один символ предпросмотра.
LL(1) – грамматики формируют основу методов
нисходящего синтаксического анализа.
◦ Если вычислены все множества первых порождаемых
символов для всех возможных правых частей продукций,
то языки, которые описываются LL(1) – грамматикой ,
всегда анализируются детерминировано
Построение анализаторов LL(K) – грамматик
слишком трудоёмко при К>1. По этой причине на
практике получили распространения лишь LL(1) –
грамматики.
25/38

26.

LL(1) – язык
LL(1) – язык – это язык, который можно сгенерировать
посредством LL(1) – грамматики.
Для любого LL(1) языка возможен нисходящий
синтаксический анализ с одним символом предпросмотра.
Существует алгоритм определения, относится ли данная
грамматика к классу LL(1).
Не существует алгоритма определения, относится ли данный
язык к классу LL(1) , т.е. имеет он LL(1) – грамматику или нет.
Не существует алгоритма, который для данной произвольной
грамматики определит, является ли генерируемый ею язык
LL(1) или нет.
26/38

27.

Левая рекурсия
Существует одно свойство грамматики, которое (если оно
присутствует) препятствует тому, чтобы грамматика была
LL(1), и это — левая рекурсия
D Dx
A BC
D y
B DE
D FG
F AH
DS ( D Dx) { y}
DS ( D y ) { y}
Ни одна леворекурсивная грамматика не является LL(1).
◦ Это не представляет такой уж серьёзной проблемы, поскольку
все левые рекурсии грамматики можно заменить правыми, не
затронув генерируемый язык.
27/38

28.

Примеры рекурсивных грамматик
Леворекурсивная грамматика со схемой:
<число> <цифра>
<число> <число><цифра>
<цифра> 1
<цифра> 0
Праворекурсивная грамматика со схемой:
<число> <цифра>
<число> <цифра><число>
<цифра> 1
<цифра> 0
28/38

29.

Формальное определение
абстрактного автомата
Абстрактный автомат определяется
пятью компонентами , Q,W , q 0 ,
множество (алфавит) входных символов
множество состояний автомата Q qi
множество выходных сигналов W wi
начальное состояние q0 Q
функция переходов Q, Q,W
ставящая в соответствие каждой паре
«состояние - входной символ» пару
состояние-выходной символ»
29/38

30.

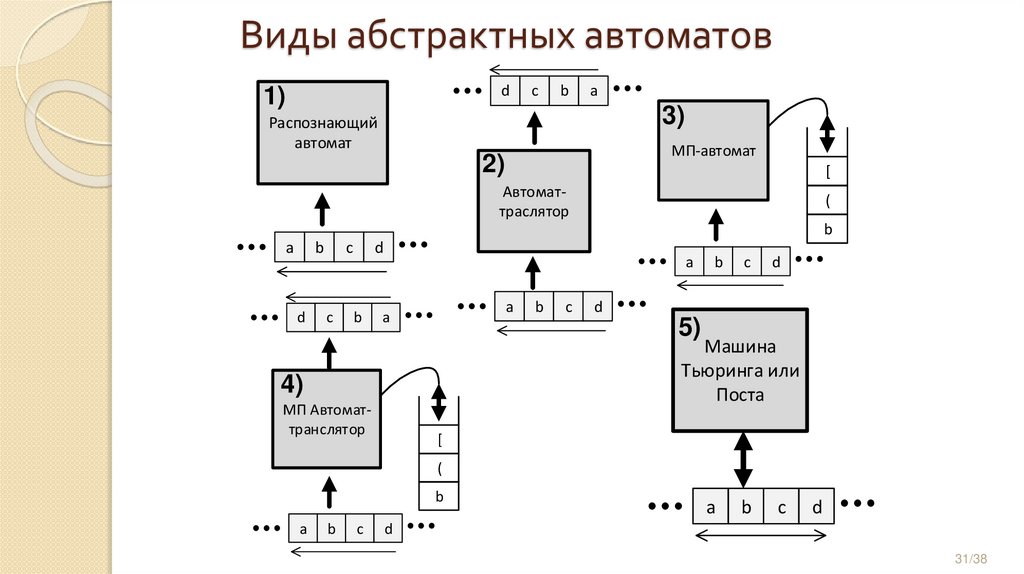
Виды абстрактных автоматов
1. Распознающий автомат – лента движется в одну сторону, символы
на ленте не изменяются
2. Автомат-транслятор – две ленты, движущиеся в одном
направлении.
3. Автомат с магазинной памятью (МП-автомат) – входная лента
движется в одном направлении и только читается. Вторая лента
выступает в роли стека (запись и чтение осуществляется только в
верхушки стека.
4. МП автомат-транслятор – считывает символы со входной ленты,
записывает на выходную ленту, промежуточные данные записывает
в стек
5. Машина Тьюринга и машина Поста – автомат может двигать ленту в
обоих направлениях и может изменять символы на ленте
30/38

31.

Виды абстрактных автоматов
d
1)
c
b
a
3)
Распознающий
автомат
МП-автомат
2)
[
Автоматтраслятор
(
b
a
b
d
c
c
d
b
a
a
a
b
c
b
c
d
d
5)
Машина
Тьюринга или
Поста
4)
МП Автоматтранслятор
[
(
b
a
b
c
a
b
c
d
d
31/38

32.

Автоматы и синтаксический анализ
a
Регулярные
c
b
грамматики =
конечный автомат
d
a
КС-грамматики =
автомат с магазинной
памятью
b
c
d
a/*/*
c/(/
b/(/(
[
(
d/*/*
b
a
b
c
d
32/38

33.

Автомат с магазинной памятью
МП автомат определяется семью
компонентами ,Q,q 0 , , z0 , , F
множество (алфавит) входных символов
множество состояний автомата Q qi
начальное состояние q0
множество допускающих состояний автомата F
множество (алфавит) магазинных символов
начальный символ магазина z0
функция переходов Q, , Q, , ставящая в
соответствие каждой тройке «состояние входной символ – верхний символ магазина»
новое состояние и цепочку магазинных символов.
33/38

34.

Определение функции переходов
для МП автомата
МП-автомат Р, находясь в состоянии q и имея в качестве
текущего входного символа a, расположенного под входной
головкой, а в качестве верхнего символа магазина - символ z,
может перейти в новое состояние q , сдвинуть входную головку
на одну ячейку вправо и заменить верхний символ магазина
цепочкой магазинных символов;
если а = ε, то входная головка не сдвигается, однако, состояние
управляющего устройства и содержимое памяти могут
измениться;
если = ε, то верхний символ удаляется из магазина
(магазинный список сокращается);
следующий такт невозможен, если магазин пуст
34/38

35.

Анализ входной строки
1.
◦
Начало
в магазине содержится единственный символ – начальный
символ
головка чтения обозревает первый символ входной ленты
◦
2.
◦
◦
◦
Автомат выполняет последовательность шагов
Анализируется символ обозреваемой головкой чтения – A
Анализируется символ находящийся в вершине автомата – B
По информации в ячейке управляющей таблицы на пересечении
строки B и столбца A определяется:
◦
3.
4.
символы которые будут помещены в магазин вместо символа
следует ли сдвигать головку чтения
Если соответствующая ячейка пуста, то – Ошибка
Если головка сошла в правого конца ленты и магазин пуст,
то – Конец
Если головка не дошла до правого края, а магазин пуст или,
головка сошла с ленты , а в магазине есть символ, то –
35/38
Ошибка

36.

КС-грамматики и МП-автоматы
Язык, допускаемый (распознаваемый, определяемый)
автоматом M (обозначается L(M)) – это множество всех
цепочек, допускаемых автоматом M.
Теорема 1. Язык допускается магазинным автоматом тогда и
только тогда, когда он допускается опустошением магазина.
Теорема 2. Язык является контекстно-свободным тогда и
только тогда, когда он допускается магазинным автоматом.
Для грамматики G (VT ,VN , P, S )
существует автомат М VТ ,{q},0,VТ VN , S , D,
такой, что если A u P, то q, u D q, , A
D ( q, a, a, ) q, для всех a VT
36/38

37.

Распознавание LL(1) – грамматики
Распознаватель для LL(1) – грамматики
строится как расширенный МП-автомат с
одним состоянием.
Управляющая таблица расширенного
МП-автомата показывает:
◦ Какая цепочка символов должна быть
записана в магазин
◦ Должен ли произойти переход к следующему
символу входной цепочки в зависимости от:
символа находящегося в вершине автомата
текущего просматриваемого символа во входной
цепочке.
Незаполненные ячейки будут указывать
на ошибки во входной строке
37/38

38.

Управляющая таблица
Терминальные символы грамматики
a2
Терминальные Нетерминальные
символы
символы
Вершина магазина
a1
A1
A2
...
aL множеству стартовых символов
, если AK :
aL множеству символов последователей AK
без сдвига
...
, сдвиг
a2
...
aM
aM
, если AK :
AN
a1
...
...
...
, сдвиг
...
...
...
...
...
, сдвиг
38/38