Петрофизическое моделирование с использованием вторичной информации. Гауссово моделирование и кригинг – Вторичные данные

1. Петрофизическое моделирование с использованием вторичной информации Гауссово моделирование и кригинг – Вторичные данные

Local Varying Mean: использует
простой кригинг и обрабатывает
вторичные данные как локально
зависимое среднее.
Collocated Co-Kriging: включает
коэффициент корреляции вторичных
данных в кригинг уравнениях.
Bivariate Distribution: Вторичное
свойство используется для
определения интервалов, в которых
будут рассматриваться разные
функции распределения, для обратного
преобразования.

2. Использование вторичных данных Локально изменяющееся среднее (m)

n
n
i
i
z ( x0 ) i z ( xi ) [1 i ]m( x 0)
• Z(xi): точки данных (например: пористость).
• m(x): вторичные входные данные такие, как 2D карта пористости или свойства с
сильно коррелированным положительным значением.
• Сумма весов
i может быть меньше, чем единица.
• Чем меньше веса, тем больше влияние локально изменяющегося среднего m(x) в
x0 на рассчитанное значение Z(x0).
• Локально изменяющееся среднее влияет сильнее, если x0 находится далеко от
точек данных (так как веса i уменьшаются ) .
ВАЖНО:
-Вторичные входные данные должны быть сглажены и определены для всех x0.
-Первичные и вторичные данные должны обладать положительной корреляцией!

3. Использование вторичных данных Пример LVM – Моделирование проницаемости, использующее пористость

Вверху: карта проницаемости: локально
изменяющееся среднее
Вверху справа: Xplot Perm-Por
Справа: гистограмма проницаемости
С уменьшением ранга вариограммы влияние
вторичных данных на результат увеличивается.

4. Использование вторичных данных Co-kriging – Общая теория

Традиционное уравнение Co-kriging: Z COK ( x0 )
Z (x ) Y (x )
i
i
i
Необходима вариограмма для первичного атрибута, для вторичного и
кроссвариограмма.
В результате громоздкая система уравнений и больше ограничений.
Collocated co-kriging:
Z CCOK ( x0 ) i Z ( xi ) μY(x 0 )
i
Возможное решение в случае большей плотности вторичного атрибута.
Необходима только вариограмма для первичного атрибута, использование
коэффициента корреляции со вторичным атрибутом
Простая система уравнений
j
j
j

5. Использование вторичных данных Collocated co-kriging – Характеристики

Упрощенные системы уравнений
быстрее, чем обычный Co-kriging
Избыточные значения вторичного атрибута не является
причиной неустойчивости
Влияющие параметры: вторичный атрибут, коэффициент
корреляции и коэффициент уменьшения дисперсии
Только вариограмма для первичного атрибута должна
быть смоделирована

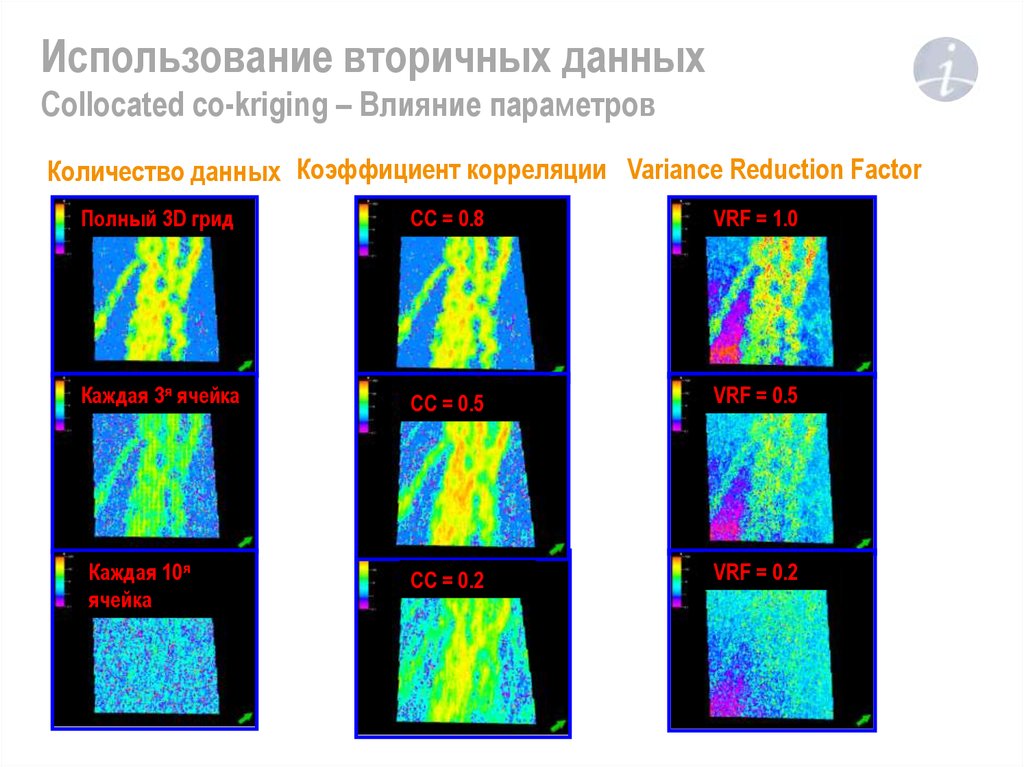
6. Использование вторичных данных Collocated co-kriging – Влияние параметров

Количество данных Коэффициент корреляции Variance Reduction Factor
Полный 3D грид
CC = 0.8
VRF = 1.0
Каждая 3я ячейка
CC = 0.5
VRF = 0.5
CC = 0.2
VRF = 0.2
Каждая 10я
ячейка

7.

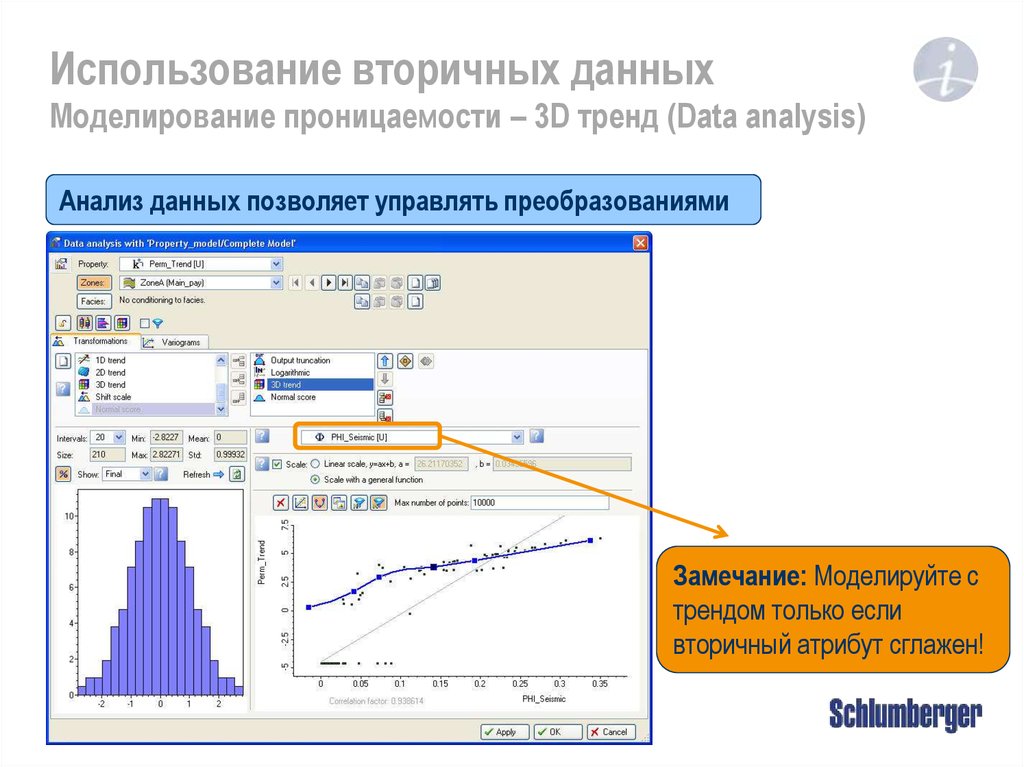
Использование вторичных данных
Моделирование проницаемости – 3D тренд (Data analysis)
Анализ данных позволяет управлять преобразованиями
Замечание: Моделируйте с
трендом только если
вторичный атрибут сглажен!

8. Использование вторичных данных Двумерное распределение – использование в обратном преобразовании

Метод двумерного распределения использует вторичное свойство,
существующее в той же области, и кросс-плот, построенный по двум
переменным, и разбитый на классы
Распределение моделируемого свойства будет зависеть от значения
вторичного свойства. Распределение будет учитываться при обратных
преобразованиях.
xplot: Пористость – Проницаемость (Log)

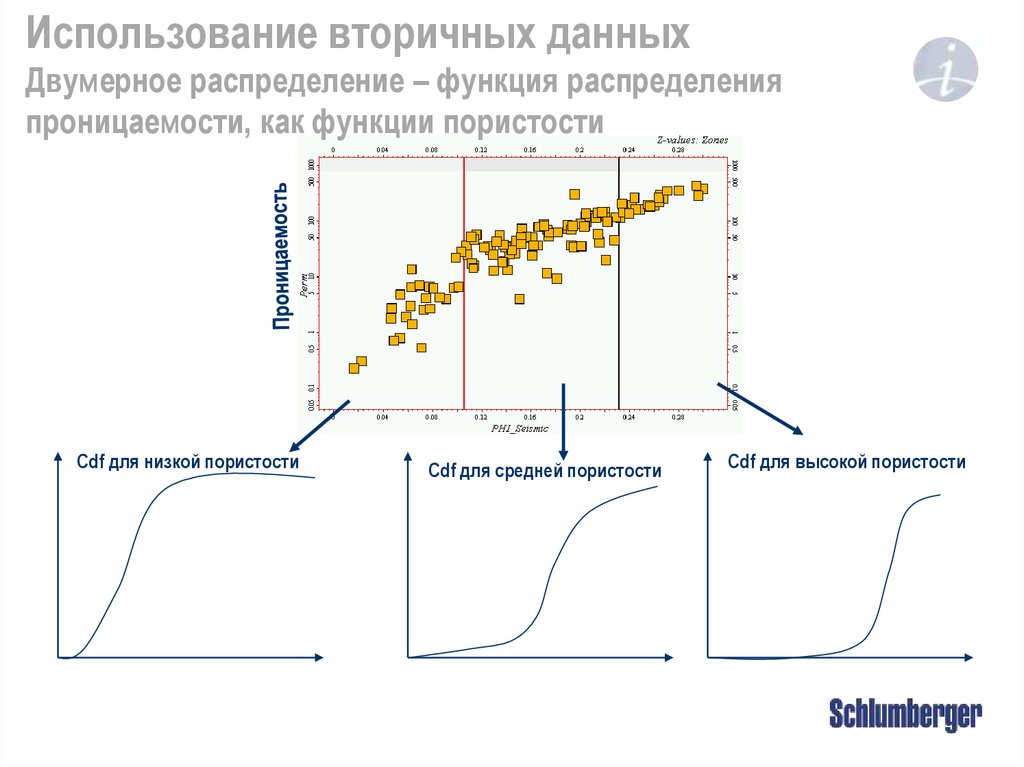
9. Использование вторичных данных Двумерное распределение – функция распределения проницаемости, как функции пористости

Cdf для низкой пористости
Cdf для средней пористости
Cdf для высокой пористости

10. Использование вторичных данных Как в кросс-плоте создать разбиение на интервалы?

Отобразите два свойства; включите
перемасштабированные ячейки
Нажмите на иконку Create a Raw
crossplot
Создайте интервалы
Выбор точек, выбор области или интервала

11. Использование вторичных данных Двумерное распределение – проницаемость, построенная с использованием пористости (разбиение на классы)

8 классов
3 класса
Смоделированная проницаемость
xplot: смоделированная проницаемость - пористость

12. Упражнения