Занятие №2. Методика решения задач методом математического моделирования в 5 классе

1.

Особенности непрерывного курса математики
«Учусь учиться» Л.Г. Петерсон
Занятие № 2. Методика решения задач методом математического
моделирования в 5 классе
Светлана Березкина
канд. физ. мат. наук, руководитель отдела математики ИСДП,
старший методист Института СДП, соавтор учебно-методических
пособий по курсу математики «Учусь учиться»
НОУ ДПО «Институт системно-деятельностной педагогики»_13.06.2023
www.peterson.institute

2.

Вы - прекрасный учитель, запомните это,
И у вас превосходные ученики.
И. Львова
ПРОГРАММА ЗАНЯТИЯ № 2
1. Рекомендации по организации урока математики –
С ЧЕГО НАЧАТЬ?
2. Особенности темы «Математический язык»
ЧТО ВАЖНО и ПОЧЕМУ?
3. Работа с РАБОЧЕЙ ТЕТРАДЬЮ—
ЧТО? ДЛЯ ЧЕГО? КАК?
4. Ответы на вопросы
ЧТО Я ВОЗЬМУ НА СВОЙ УРОК?
5. Рефлексия занятия № 2
www.peterson.institute

3.

Вы - прекрасный учитель, запомните это,
И у вас превосходные ученики.
И. Львова
РЕКОМЕНДАЦИИ ПО ОРГАНИЗАЦИИ УРОКА МАТЕМАТИКИ – С ЧЕГО НАЧАТЬ?
1. Создайте в классе СРЕДУ ДОВЕРИЯ, УВАЖЕНИЯ, ТВОРЧЕСТВА, РАДОСТИ («на любовь свое сердце
настройте!»).
2. Опирайтесь на свой привычный инструментарий, вводя ИЗ НОВОГО ТОЛЬКО ТО, ЧТО ПОНРАВИЛОСЬ.
3. Изучите Задачи для самоконтроля по главе, и СДЕЛАЙТЕ ВЫБОР ЗАДАЧ УЧЕБНИКА так, чтобы объем
был
посильным.
4. Проверку домашнего задания ЗАМЕНИТЕ САМОПРОВЕРКОЙ по подробному образцу (готовому
решению).
5. Используйте прием ВЫБОРА ЗАДАЧ ДЕТЬМИ «ПО ЖЕЛАНИЮ».
Л.Г. Петерсон
6. Проанализируйте свои уроки с целью ИСКЛЮЧЕНИЯ ПОТЕРЬ ВРЕМЕНИ.
7. Каждый день ФИКСИРУЙТЕ УСПЕХИ СВОИ И ДЕТЕЙ.
8. Просмотрите УЧЕБНИКИ 3‒4 КЛАССА (Л.Г. ПЕТЕРСОН), чтобы понять логику развития содержания.
9. РАБОТАЙТЕ СПОКОЙНО И С УДОВОЛЬСТВИЕМ ‒ У ВАС ВСЕ ПОЛУЧИТСЯ!

4.

Повторяя, узнаю НОВОЕ
Л. Петерсон
ОСОБЕННОСТИ ТЕМЫ «МАТЕМАТИЧЕСКИЙ ЯЗЫК». ЧТО ВАЖНО И ПОЧЕМУ?
5 класс. Часть 1. Глава 1.
43 ч
Математический язык
§ 1. Математические выражения
1. Запись, чтение и составление выражений.
2. Значение выражения.
§ 2. Математические модели
1. Перевод условия задачи на математический язык.
2. Работа с математическими моделями.
3. Метод проб и ошибок.
4. Метод перебора.
§ 3. Язык и логика
Цели
Сформировать представление о математическом языке
как о языке описания законов окружающего мира, и о
математических моделях реальной действительности.
Формировать умение строить математические модели
текстовых задач; умение использовать буквенные
выражения, схемы, таблицы.
Познакомить с методами работы с математическими
моделями (повторить известные способы и формировать
умение их применять);
1. Высказывания.
Подготовить основу для изучения делимости чисел.
2. Общие утверждения.
Создать условия для мотивации к изучению математики
3. «Хотя бы один».
4. О доказательстве общих утверждений.
5. Введение обозначений.

5.

Природа говорит языком математики.
Галилео Галилей
ОСОБЕННОСТИ ТЕМЫ «МАТЕМАТИЧЕСКИЙ ЯЗЫК». ЧТО ВАЖНО И ПОЧЕМУ?
5 класс. Часть 1. Глава 1.
Особенности изучения
Дается представление о математике как языке, описывающем
закономерные связи и отношения реального мира.
Первый этап математического моделирования – построение
математической модели – является «переводческой» работой
текстов русского языка на математический и наоборот.
Изучение различных способов работы с математическими
моделями начинается с повторения известных способов, затем
продолжается знакомством с общенаучными методами
исследования реального мира – методом проб и ошибок и
методом перебора.
ВЕЛИКАЯ ТАЙНА МАТЕМАТИКИ
https://www.youtube.com/watch?v=kF14qJbRXds
Знакомство с различными видами высказываний позволяет
учиться обосновывать и опровергать их.
Знакомство с новыми вопросами осуществляется на материале,
изученном, детьми в начальной школе.

6.

В одиночку можно сделать так мало,
но вместе можно сделать так много.
Хелен Адамс Келлер
ОСОБЕННОСТИ ТЕМЫ «МАТЕМАТИЧЕСКИЙ ЯЗЫК». ЧТО ВАЖНО И ПОЧЕМУ?
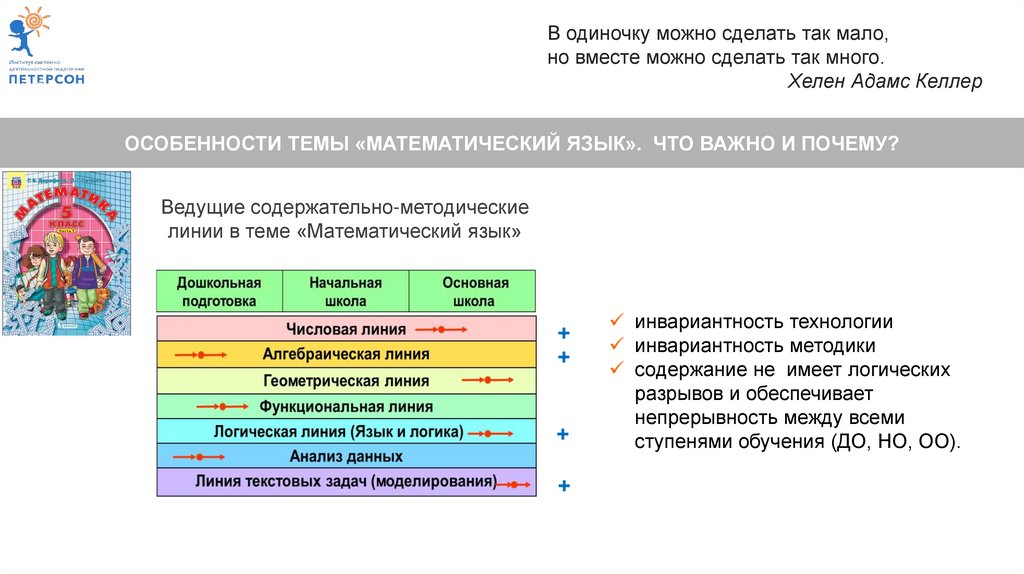
Ведущие содержательно-методические
линии в теме «Математический язык»
+
+
+
+
инвариантность технологии
инвариантность методики
содержание не имеет логических
разрывов и обеспечивает
непрерывность между всеми
ступенями обучения (ДО, НО, ОО).

7.

Понимание и грамотное использование
математического языка
ОСОБЕННОСТИ ТЕМЫ «МАТЕМАТИЧЕСКИЙ ЯЗЫК». ЧТО ВАЖНО И ПОЧЕМУ?
§ 1. Математические выражения
1. Запись, чтение и составление выражений.
2. Значение выражения.
Цели
Сформировать представление о математических выражениях как о
«словах» математического языка, уточнить понятия числового и
буквенного выражений.
Особенности изучения
Дается представление о математике как языке, описывающем
закономерные связи и отношения реального мира.
Сформировать умение «переводить» тексты с русского языка на
математический, и наоборот.
С первых уроков ведется работа по выделению из математических
записей математических выражений и определение вида
математических выражений.
Уточнить понятие «значение выражения», повторить нахождение
значения буквенного выражения при данных значениях букв.
Осваивается прием записи математических выражений, опуская знак
умножения.
Уроки готовят учащихся к теме «Математические модели».

8.

Понимание и грамотное использование
математического языка
ОСОБЕННОСТИ ТЕМЫ «МАТЕМАТИЧЕСКИЙ ЯЗЫК». ЧТО ВАЖНО И ПОЧЕМУ?
§ 1. Математические выражения
1. Запись, чтение и составление выражений.
2. Значение выражения.
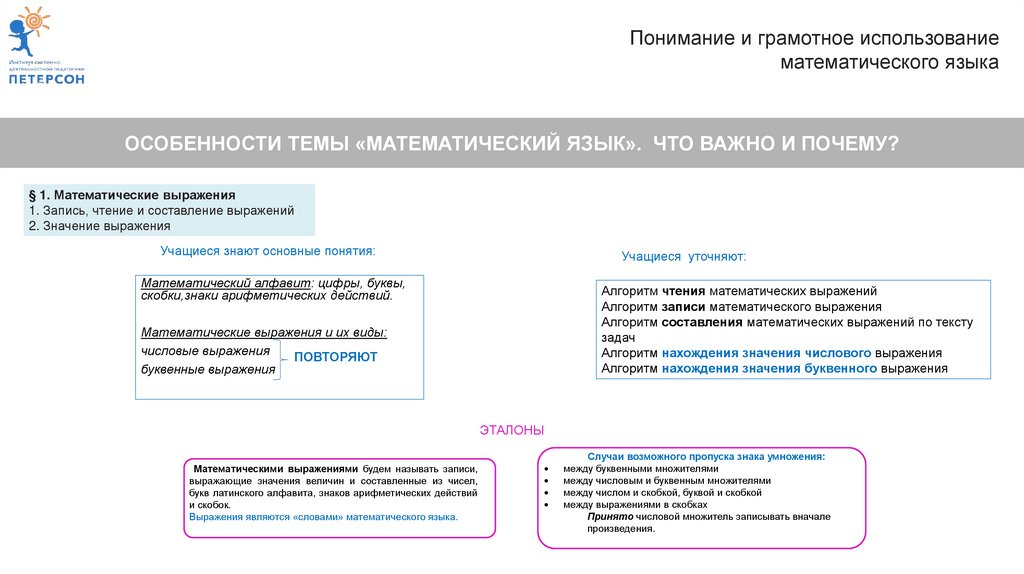
Учащиеся знают основные понятия:
Учащиеся уточняют:
Математический алфавит: цифры, буквы,
скобки,знаки арифметических действий.
Алгоритм чтения математических выражений
Алгоритм записи математического выражения
Алгоритм составления математических выражений по тексту
задач
Алгоритм нахождения значения числового выражения
Алгоритм нахождения значения буквенного выражения
Математические выражения и их виды:
числовые выражения
ПОВТОРЯЮТ
буквенные выражения
ЭТАЛОНЫ
Математическими выражениями будем называть записи,
выражающие значения величин и составленные из чисел,
букв латинского алфавита, знаков арифметических действий
и скобок.
Выражения являются «словами» математического языка.
Случаи возможного пропуска знака умножения:
между буквенными множителями
между числовым и буквенным множителями
между числом и скобкой, буквой и скобкой
между выражениями в скобках
Принято числовой множитель записывать вначале
произведения.

9.

В одиночку можно сделать так мало,
но вместе можно сделать так много.
Хелен Адамс Келлер
ОСОБЕННОСТИ ТЕМЫ «МАТЕМАТИЧЕСКИЙ ЯЗЫК». ЧТО ВАЖНО И ПОЧЕМУ?
Задание 1. Проанализируйте задания из учебника «М-5»,Ч.1 № 11, 16 и 40.
Ответьте на вопросы:
1) В чем содержательное приращение при переходе от № 11 к № 16 и к № 40?
2) На что работают данные задания? (перечислите содержательные и
методические особенности данных заданий)
Методика
организации
работы в группе

10.

В одиночку можно сделать так мало,
но вместе можно сделать так много.
Хелен Адамс Келлер
ОСОБЕННОСТИ ТЕМЫ «МАТЕМАТИЧЕСКИЙ ЯЗЫК». ЧТО ВАЖНО И ПОЧЕМУ?
Задание 1. Проанализируйте задания из учебника «М-5»,Ч.1 № 11, 16 и 40.
Ответьте на вопросы:
1) В чем содержательное приращение при переходе от № 11 к № 16 и к № 40?
2) На что работают данные задания? (перечислите содержательные и
методические особенности данных заданий)
НЕПРЕРЫВНОСТЬ В СОДЕРЖАНИИ, МЕТОДИКЕ
учебное содержание выстраивается как система задач, каждая из которых
может быть выведена из предыдущих на основании предыдущего опыта:
содержание не должно иметь логических разрывов и обеспечивать
непрерывность между всеми ступенями обучения (ДО, НО, ОО).
3 класс

11.

Понимание и грамотное использование
математического языка
ОСОБЕННОСТИ ТЕМЫ «МАТЕМАТИЧЕСКИЙ ЯЗЫК». ЧТО ВАЖНО И ПОЧЕМУ?
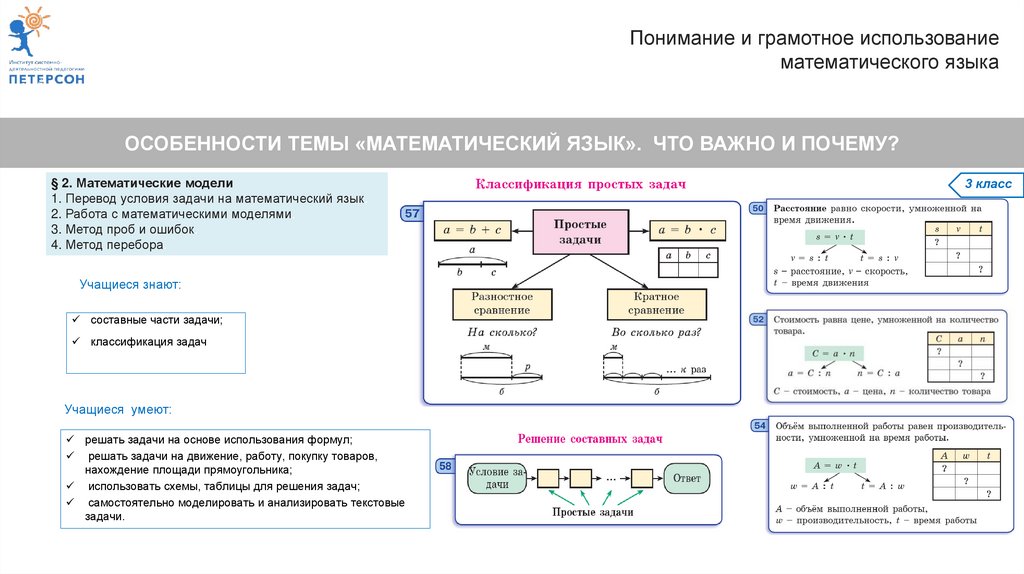
§ 2. Математические модели
1. Перевод условия задачи на математический язык.
2. Работа с математическими моделями.
3. Метод проб и ошибок.
4. Метод перебора.
Цели
Формировать:
представление о математических моделях реальной
действительности;
умение строить математические модели текстовых задач;
умение использовать буквенные выражения, схемы, таблицы;
умение работать с математическими моделями (повторить известные
способы);
представление о методе проб и ошибок;
представление о методе полного перебора.
Особенности изучения
Изучение темы хорошо подготовлено содержанием курса математики
начальной школы.
Содержание данного параграфа разбивается на два этапа: на первом
отрабатывается умение составлять математические модели по тексту
задачи, а на втором разбираются способы работы с полученными
моделями и их применение для получения ответа на вопрос задачи.

12.

Понимание и грамотное использование
математического языка
ОСОБЕННОСТИ ТЕМЫ «МАТЕМАТИЧЕСКИЙ ЯЗЫК». ЧТО ВАЖНО И ПОЧЕМУ?
§ 2. Математические модели
1. Перевод условия задачи на математический язык.
2. Работа с математическими моделями.
3. Метод проб и ошибок.
4. Метод перебора.
Учащиеся знают:
составные части задачи;
классификация задач
Учащиеся умеют:
решать задачи на основе использования формул;
решать задачи на движение, работу, покупку товаров,
нахождение площади прямоугольника;
использовать схемы, таблицы для решения задач;
самостоятельно моделировать и анализировать текстовые
задачи.
3 класс

13.

Понимание и грамотное использование
математического языка
ОСОБЕННОСТИ ТЕМЫ «МАТЕМАТИЧЕСКИЙ ЯЗЫК». ЧТО ВАЖНО И ПОЧЕМУ?
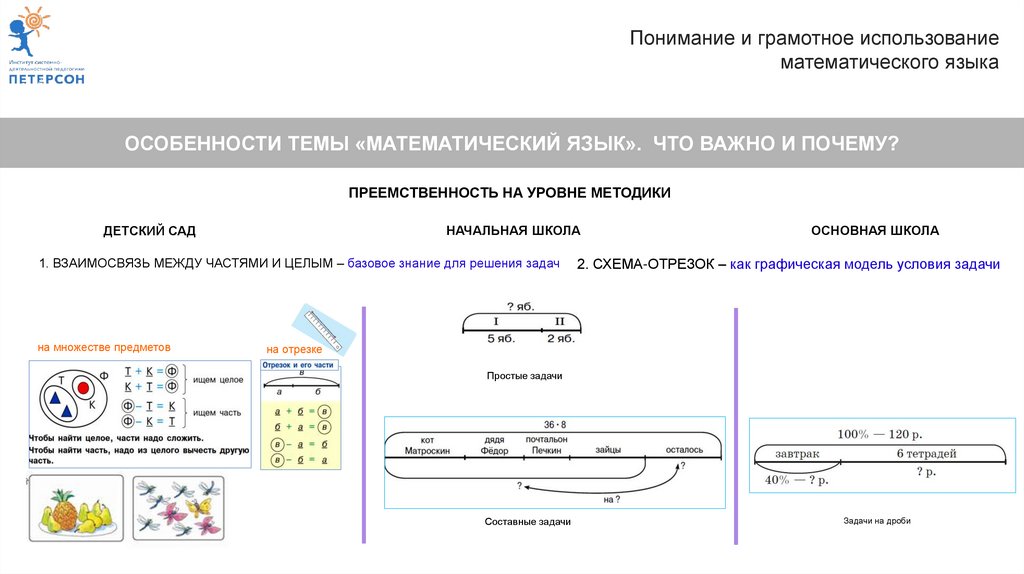
ПРЕЕМСТВЕННОСТЬ НА УРОВНЕ МЕТОДИКИ
НАЧАЛЬНАЯ ШКОЛА
ДЕТСКИЙ САД
1. ВЗАИМОСВЯЗЬ МЕЖДУ ЧАСТЯМИ И ЦЕЛЫМ – базовое знание для решения задач
на множестве предметов
ОСНОВНАЯ ШКОЛА
2. СХЕМА-ОТРЕЗОК – как графическая модель условия задачи
на отрезке
Простые задачи
Составные задачи
Задачи на дроби

14.

Метод математического моделирования
ОСОБЕННОСТИ ТЕМЫ «МАТЕМАТИЧЕСКИЙ ЯЗЫК». ЧТО ВАЖНО И ПОЧЕМУ?
ПРЕЕМСТВЕННОСТЬ НА УРОВНЕ МЕТОДИКИ
НАЧАЛЬНАЯ ШКОЛА
ОСНОВНАЯ ШКОЛА
3. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ
Алгоритм решения задачи
1. Внимательно прочитать задачу.
2. Определить условие и вопрос задачи
(если нужно, составить схему).
3. Определить, каким действием надо ответить
на вопрос задачи.
4. Можно ли сразу ответить на вопрос задачи?
Если нет, то найти неизвестные величины.
5. Решить задачу и найти ответ.
Комментирование решения составной задачи
1. Внимательно прочитаю задачу: …
2. Известно ... Надо найти ...
3. Чтобы ответить на вопрос задачи, надо ..., так как ...
4. Сразу не могу ответить на вопрос задачи, так как ...
5. Поэтому в первом действии ...,
во втором действии ...
6. Ответ: ...
Алгоритм решения задач методом
математического моделирования
I. Построение математической модели
1. Внимательно прочитать задачу и определить, что
известно и что нужно найти.
2. Проверить соответствие единиц счёта / измерения
величин (при необходимости выполнить их преобразование).
3. Установить взаимосвязи между описанными в ней
величинами (можно использовать формулы, схемы,
таблицы). Если нужно, одну или несколько неизвестных
величин обозначить буквами.
4. Построить математическую модель задачи (выражение,
уравнение и др.).
5. Зафиксировать искомую величину и её возможные значения.
II. Работа с математической моделью.
6. Найти все решения, удовлетворяющие построенной модели.
III. Практический вывод.
7. Проверить соответствие полученного ответа условию,
вопросу и смыслу задачи.

15.

Что важно и почему?
ОСОБЕННОСТИ ТЕМЫ «МАТЕМАТИЧЕСКИЙ ЯЗЫК». ЧТО ВАЖНО И ПОЧЕМУ?
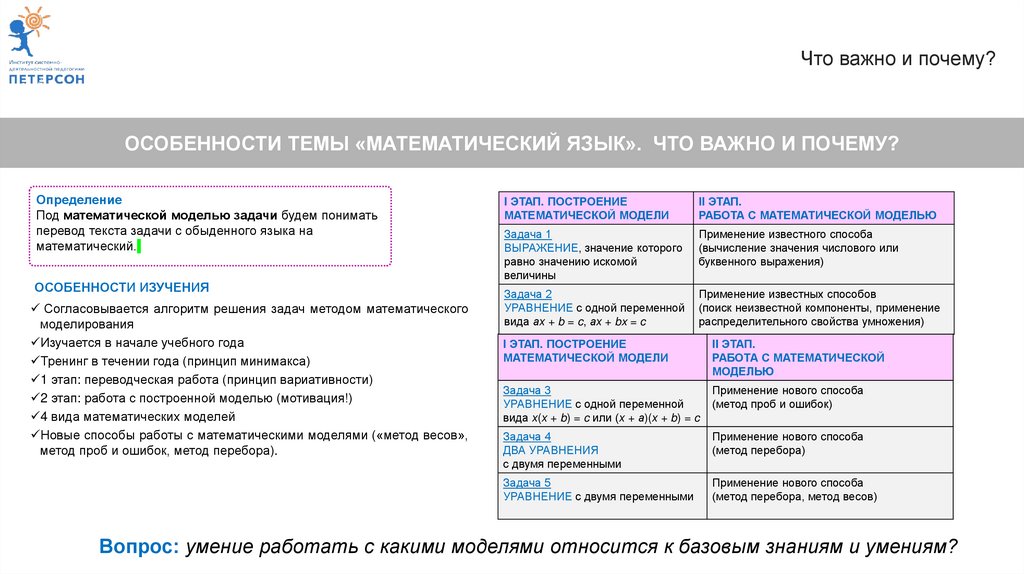
Определение
Под математической моделью задачи будем понимать
перевод текста задачи с обыденного языка на
математический.
ОСОБЕННОСТИ ИЗУЧЕНИЯ
Согласовывается алгоритм решения задач методом математического
моделирования
Изучается в начале учебного года
Тренинг в течении года (принцип минимакса)
1 этап: переводческая работа (принцип вариативности)
2 этап: работа с построенной моделью (мотивация!)
4 вида математических моделей
Новые способы работы с математическими моделями («метод весов»,
метод проб и ошибок, метод перебора).

16.

Что важно и почему?
ОСОБЕННОСТИ ТЕМЫ «МАТЕМАТИЧЕСКИЙ ЯЗЫК». ЧТО ВАЖНО И ПОЧЕМУ?
Определение
Под математической моделью задачи будем понимать
перевод текста задачи с обыденного языка на
математический.
ОСОБЕННОСТИ ИЗУЧЕНИЯ
Согласовывается алгоритм решения задач методом математического
моделирования
Изучается в начале учебного года
Тренинг в течении года (принцип минимакса)
1 этап: переводческая работа (принцип вариативности)
2 этап: работа с построенной моделью (мотивация!)
4 вида математических моделей
Новые способы работы с математическими моделями («метод весов»,
метод проб и ошибок, метод перебора).
I ЭТАП. ПОСТРОЕНИЕ
МАТЕМАТИЧЕСКОЙ МОДЕЛИ
II ЭТАП.
РАБОТА С МАТЕМАТИЧЕСКОЙ МОДЕЛЬЮ
Задача 1
ВЫРАЖЕНИЕ, значение которого
равно значению искомой
величины
Применение известного способа
(вычисление значения числового или
буквенного выражения)
Задача 2
УРАВНЕНИЕ с одной переменной
вида ах + b = c, ах + bx = c
Применение известных способов
(поиск неизвестной компоненты, применение
распределительного свойства умножения)
I ЭТАП. ПОСТРОЕНИЕ
МАТЕМАТИЧЕСКОЙ МОДЕЛИ
II ЭТАП.
РАБОТА С МАТЕМАТИЧЕСКОЙ
МОДЕЛЬЮ
Задача 3
УРАВНЕНИЕ с одной переменной
вида х(х + b) = c или (х + а)(х + b) = c
Применение нового способа
(метод проб и ошибок)
Задача 4
ДВА УРАВНЕНИЯ
с двумя переменными
Применение нового способа
(метод перебора)
Задача 5
УРАВНЕНИЕ с двумя переменными
Применение нового способа
(метод перебора, метод весов)
Вопрос: умение работать с какими моделями относится к базовым знаниям и умениям?

17.

Что важно и почему?
ОСОБЕННОСТИ ТЕМЫ «МАТЕМАТИЧЕСКИЙ ЯЗЫК». ЧТО ВАЖНО И ПОЧЕМУ?
Определение
Под математической моделью задачи будем понимать
перевод текста задачи с обыденного языка на
математический.
ОСОБЕННОСТИ ИЗУЧЕНИЯ
Согласовывается алгоритм решения задач методом математического
моделирования
Изучается в начале учебного года
Тренинг в течении года (принцип минимакса)
1 этап: переводческая работа (принцип вариативности)
2 этап: работа с построенной моделью (мотивация!)
4 вида математических моделей
Новые способы работы с математическими моделями («метод весов»,
метод проб и ошибок, метод перебора).
I ЭТАП. ПОСТРОЕНИЕ
МАТЕМАТИЧЕСКОЙ МОДЕЛИ
II ЭТАП.
РАБОТА С МАТЕМАТИЧЕСКОЙ МОДЕЛЬЮ
Задача 1
ВЫРАЖЕНИЕ, значение которого
равно значению искомой
величины
Применение известного способа
(вычисление значения числового или
буквенного выражения)
Задача 2
УРАВНЕНИЕ с одной переменной
вида ах + b = c, ах + bx = c
Применение известных способов
(поиск неизвестной компоненты, применение
распределительного свойства умножения)
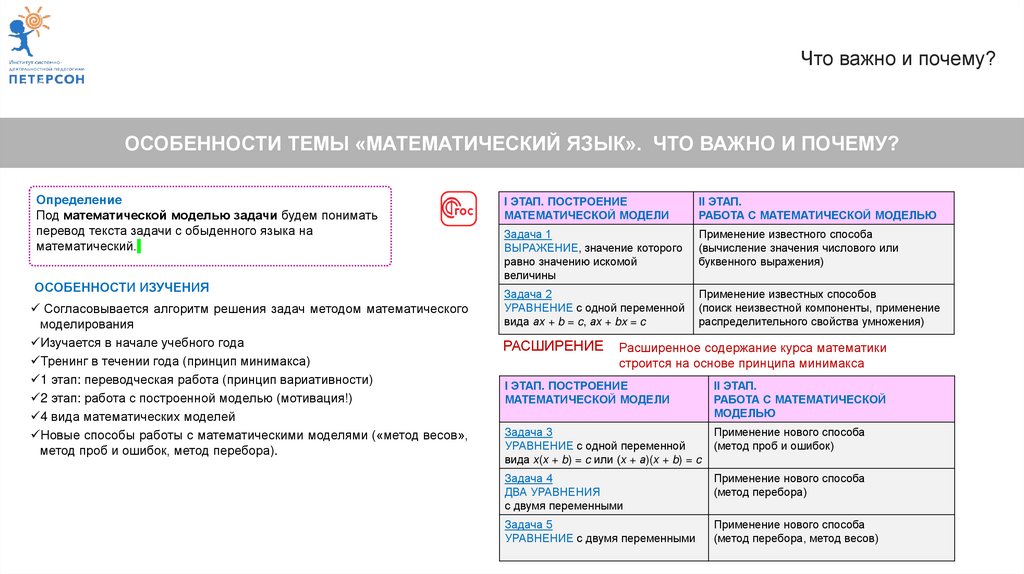
РАСШИРЕНИЕ
Расширенное содержание курса математики
строится на основе принципа минимакса
I ЭТАП. ПОСТРОЕНИЕ
МАТЕМАТИЧЕСКОЙ МОДЕЛИ
II ЭТАП.
РАБОТА С МАТЕМАТИЧЕСКОЙ
МОДЕЛЬЮ
Задача 3
УРАВНЕНИЕ с одной переменной
вида х(х + b) = c или (х + а)(х + b) = c
Применение нового способа
(метод проб и ошибок)
Задача 4
ДВА УРАВНЕНИЯ
с двумя переменными
Применение нового способа
(метод перебора)
Задача 5
УРАВНЕНИЕ с двумя переменными
Применение нового способа
(метод перебора, метод весов)

18.

МАТЕМАТИЧЕСКИЙ ЯЗЫК
§ 2. Математические модели
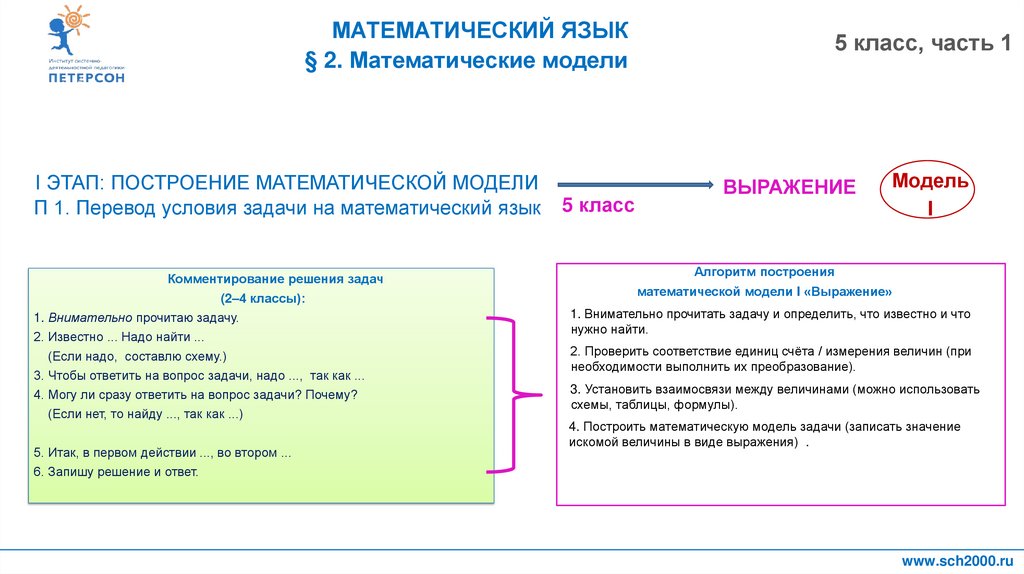
I ЭТАП: ПОСТРОЕНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ
П 1. Перевод условия задачи на математический язык
Построй математическую модель задачи:
В зоопарке было 35 львов, носорогов, обезьян и крокодилов. Львов
было 6, носорогов на 2 меньше, чем львов, а обезьян в 5 раз больше,
чем носорогов. Сколько крокодилов было в этом зоопарке?
Найди выражение, которое является правильным переводом задачи на
математический язык. Придумай задачу с другими величинами,
имеющую такое же решение.
а) Из с метров шёлка сшили 7 одинаковых платьев. Сколько метров
шёлка потребуется на 12 таких платьев?
5 класс, часть 1
ВЫРАЖЕНИЕ
Модель
I
Модель
I
1) (с : 7) : 12;
2) (с : 7) ·12;
3) 12 : (с : 7);
4) (с ·7) ·12.
www.sch2000.ru

19.

МАТЕМАТИЧЕСКИЙ ЯЗЫК
§ 2. Математические модели
I ЭТАП: ПОСТРОЕНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ
П 1. Перевод условия задачи на математический язык
Комментирование решения задач
(2–4 классы):
1. Внимательно прочитаю задачу.
2. Известно ... Надо найти ...
(Если надо, составлю схему.)
3. Чтобы ответить на вопрос задачи, надо ..., так как ...
4. Могу ли сразу ответить на вопрос задачи? Почему?
(Если нет, то найду ..., так как ...)
5. Итак, в первом действии ..., во втором ...
6. Запишу решение и ответ.
5 класс
5 класс, часть 1
ВЫРАЖЕНИЕ
Модель
I
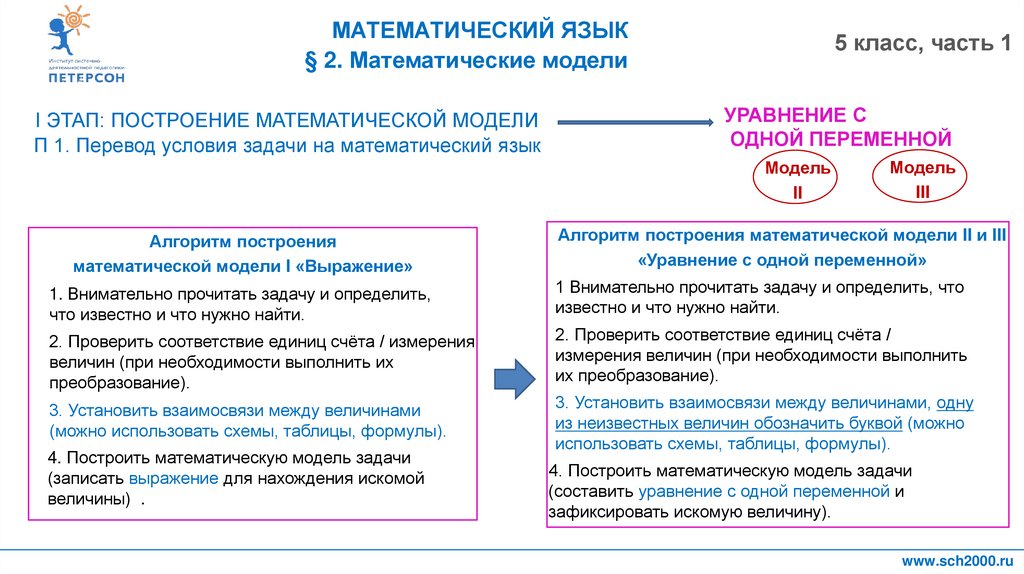
Алгоритм построения
математической модели I «Выражение»
1. Внимательно прочитать задачу и определить, что известно и что
нужно найти.
2. Проверить соответствие единиц счёта / измерения величин (при
необходимости выполнить их преобразование).
3. Установить взаимосвязи между величинами (можно использовать
схемы, таблицы, формулы).
4. Построить математическую модель задачи (записать значение
искомой величины в виде выражения) .
www.sch2000.ru

20.

МАТЕМАТИЧЕСКИЙ ЯЗЫК
§ 2. Математические модели
I ЭТАП: ПОСТРОЕНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ
П 1. Перевод условия задачи на математический язык
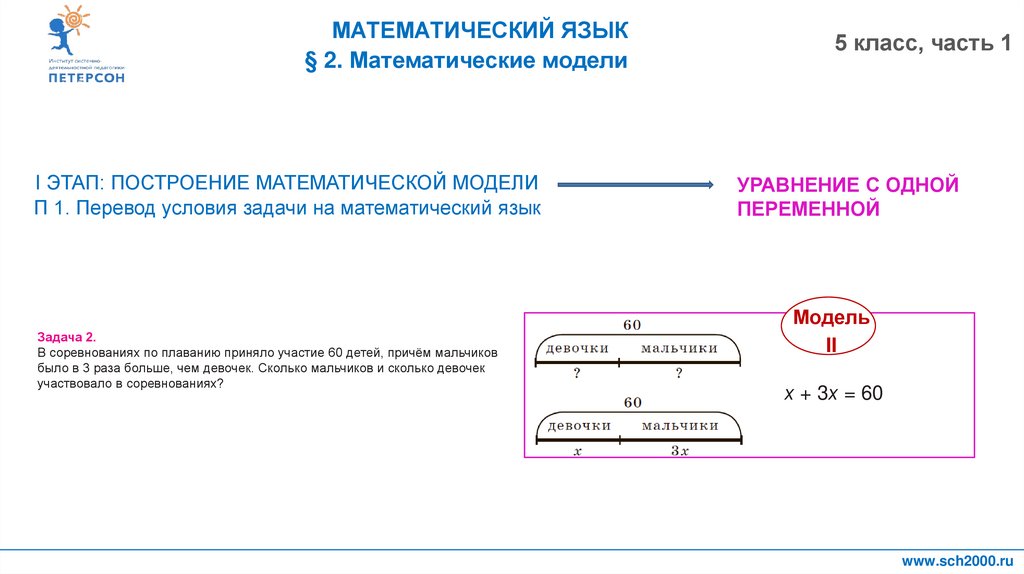
Задача 2.
В соревнованиях по плаванию приняло участие 60 детей, причём мальчиков
было в 3 раза больше, чем девочек. Сколько мальчиков и сколько девочек
участвовало в соревнованиях?
5 класс, часть 1
УРАВНЕНИЕ С ОДНОЙ
ПЕРЕМЕННОЙ
Модель
II
х + 3х = 60
www.sch2000.ru

21.

МАТЕМАТИЧЕСКИЙ ЯЗЫК
§ 2. Математические модели
I ЭТАП: ПОСТРОЕНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ
П 1. Перевод условия задачи на математический язык
5 класс, часть 1
УРАВНЕНИЕ С ОДНОЙ
ПЕРЕМЕННОЙ
Модель
II
Задача 2.
В соревнованиях по плаванию приняло участие 60 детей, причём мальчиков
было в 3 раза больше, чем девочек. Сколько мальчиков и сколько девочек
участвовало в соревнованиях?
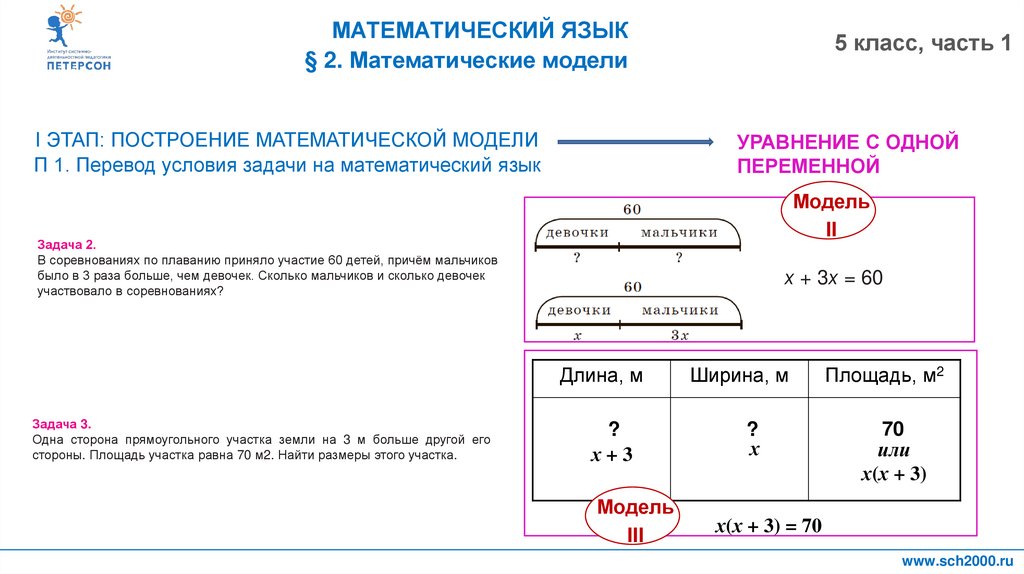
Задача 3.
Одна сторона прямоугольного участка земли на 3 м больше другой его
стороны. Площадь участка равна 70 м2. Найти размеры этого участка.
х + 3х = 60
Длина, м
Ширина, м
Площадь, м2
?
х+3
?
х
70
или
х(х + 3)
Модель
III
х(х + 3) = 70
www.sch2000.ru

22.

МАТЕМАТИЧЕСКИЙ ЯЗЫК
§ 2. Математические модели
I ЭТАП: ПОСТРОЕНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ
П 1. Перевод условия задачи на математический язык
5 класс, часть 1
УРАВНЕНИЕ С
ОДНОЙ ПЕРЕМЕННОЙ
Модель
II
Алгоритм построения
математической модели I «Выражение»
Модель
III
Алгоритм построения математической модели II и III
«Уравнение с одной переменной»
1. Внимательно прочитать задачу и определить,
что известно и что нужно найти.
1 Внимательно прочитать задачу и определить, что
известно и что нужно найти.
2. Проверить соответствие единиц счёта / измерения
величин (при необходимости выполнить их
преобразование).
2. Проверить соответствие единиц счёта /
измерения величин (при необходимости выполнить
их преобразование).
3. Установить взаимосвязи между величинами
(можно использовать схемы, таблицы, формулы).
3. Установить взаимосвязи между величинами, одну
из неизвестных величин обозначить буквой (можно
использовать схемы, таблицы, формулы).
4. Построить математическую модель задачи
(записать выражение для нахождения искомой
величины) .
4. Построить математическую модель задачи
(составить уравнение с одной переменной и
зафиксировать искомую величину).
www.sch2000.ru

23.

5 класс, часть 1
МАТЕМАТИЧЕСКИЙ ЯЗЫК
§ 2. Математические модели
ДВА УРАВНЕНИЯ С ДВУМЯ
ПЕРЕМЕННЫМ
I ЭТАП: ПОСТРОЕНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ
П 1. Перевод условия задачи на математический язык
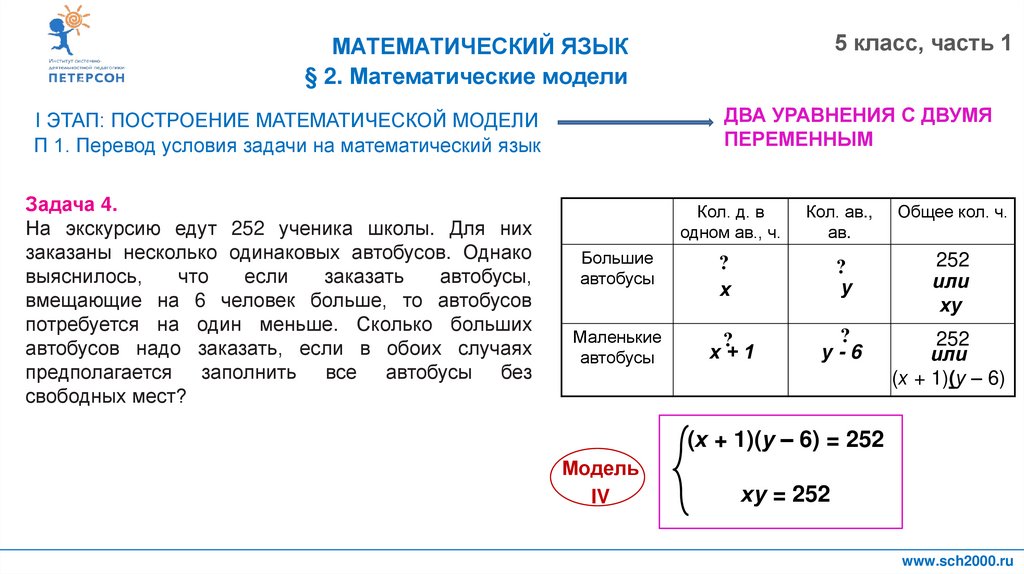
Задача 4.
На экскурсию едут 252 ученика школы. Для них
заказаны несколько одинаковых автобусов. Однако
выяснилось,
что
если
заказать
автобусы,
вмещающие на 6 человек больше, то автобусов
потребуется на один меньше. Сколько больших
автобусов надо заказать, если в обоих случаях
предполагается заполнить все автобусы без
свободных мест?
Кол. д. в
одном ав., ч.
Кол. ав.,
ав.
Общее кол. ч.
Большие
автобусы
?
х
?
у
252
или
ху
Маленькие
автобусы
?
х+1
?
у-6
252
или
(х + 1)(у – 6)
(х + 1)(у – 6) = 252
Модель
IV
ху = 252
www.sch2000.ru

24.

МАТЕМАТИЧЕСКИЙ ЯЗЫК
§ 2. Математические модели
I ЭТАП: ПОСТРОЕНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ
П 1. Перевод условия задачи на математический язык
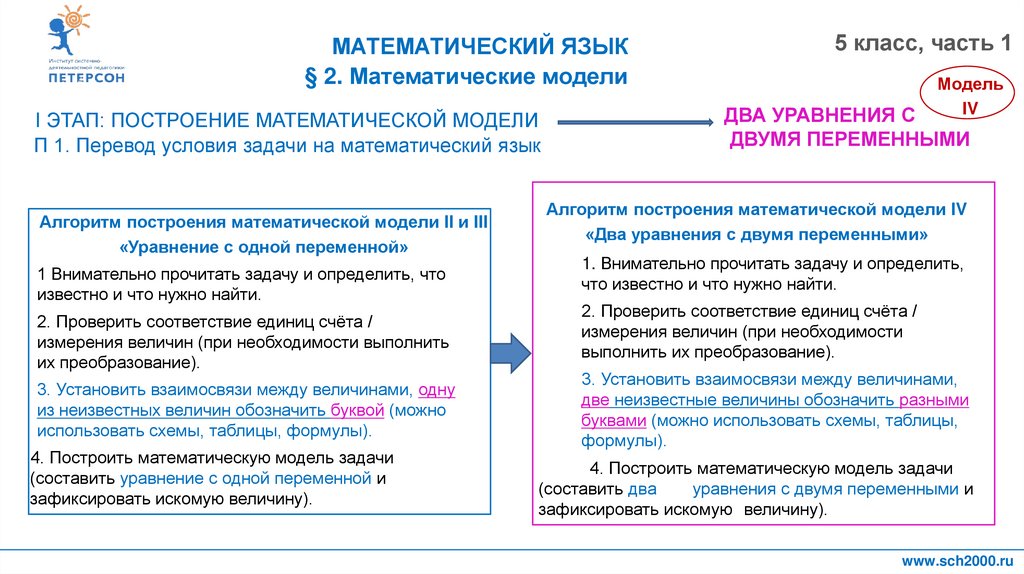
Алгоритм построения математической модели II и III
«Уравнение с одной переменной»
1 Внимательно прочитать задачу и определить, что
известно и что нужно найти.
2. Проверить соответствие единиц счёта /
измерения величин (при необходимости выполнить
их преобразование).
3. Установить взаимосвязи между величинами, одну
из неизвестных величин обозначить буквой (можно
использовать схемы, таблицы, формулы).
4. Построить математическую модель задачи
(составить уравнение с одной переменной и
зафиксировать искомую величину).
5 класс, часть 1
Модель
IV
ДВА УРАВНЕНИЯ С
ДВУМЯ ПЕРЕМЕННЫМИ
Алгоритм построения математической модели IV
«Два уравнения с двумя переменными»
1. Внимательно прочитать задачу и определить,
что известно и что нужно найти.
2. Проверить соответствие единиц счёта /
измерения величин (при необходимости
выполнить их преобразование).
3. Установить взаимосвязи между величинами,
две неизвестные величины обозначить разными
буквами (можно использовать схемы, таблицы,
формулы).
4. Построить математическую модель задачи
(составить два
уравнения с двумя переменными и
зафиксировать искомую величину).
www.sch2000.ru

25.

5 класс, часть 1
МАТЕМАТИЧЕСКИЙ ЯЗЫК
§ 2. Математические модели
I ЭТАП: ПОСТРОЕНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ
П 1. Перевод условия задачи на математический язык
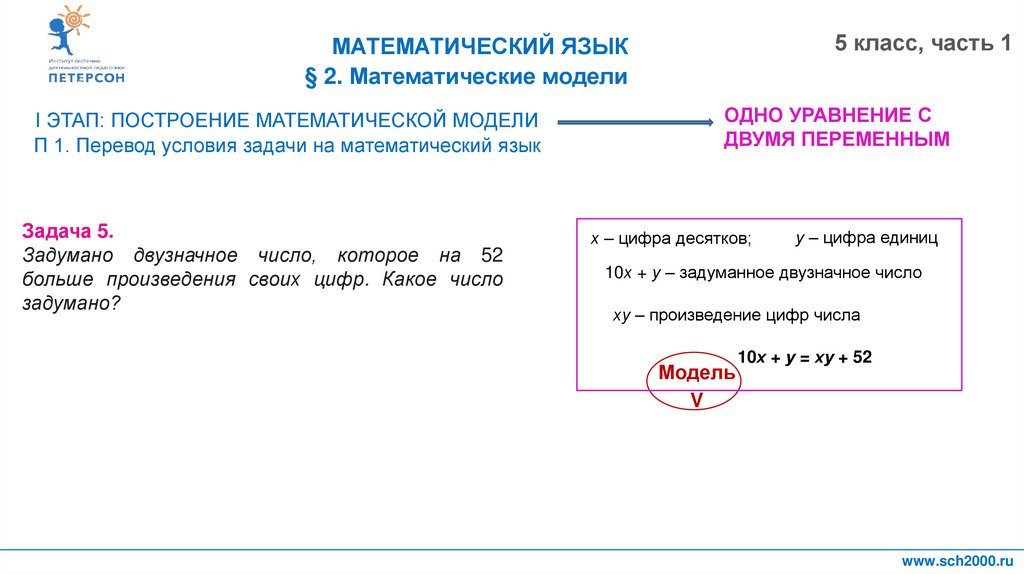
Задача 5.
Задумано двузначное число, которое на 52
больше произведения своих цифр. Какое число
задумано?
ОДНО УРАВНЕНИЕ С
ДВУМЯ ПЕРЕМЕННЫМ
х – цифра десятков;
у – цифра единиц
10х + у – задуманное двузначное число
ху – произведение цифр числа
Модель
V
10х + у = ху + 52
www.sch2000.ru

26.

МАТЕМАТИЧЕСКИЙ ЯЗЫК
§ 2. Математические модели
I ЭТАП: ПОСТРОЕНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ
П 1. Перевод условия задачи на математический язык
Алгоритм построения математической модели IV
«Два уравнения с двумя переменными»
1. Внимательно прочитать задачу и определить,
что известно и что нужно найти.
2. Проверить соответствие единиц счёта /
измерения величин (при необходимости
выполнить их преобразование).
3. Установить взаимосвязи между величинами,
две неизвестные величины обозначить разными
буквами (можно использовать схемы, таблицы,
формулы).
4. Построить математическую модель задачи
(составить два
уравнения с двумя переменными и
зафиксировать искомую величину).
5 класс, часть 1
Модель
V
ОДНО УРАВНЕНИЕ С
ДВУМЯ ПЕРЕМЕННЫМИ
Алгоритм построения математической модели V
«Одно уравнение с двумя переменными»:
1. Внимательно прочитать задачу и определить, что
известно и что нужно найти.
2. Проверить соответствие единиц счёта /
измерения величин (при необходимости выполнить
их преобразование).
3. Установить взаимосвязи между величинами, две
неизвестные величины обозначить разными
буквами (можно использовать схемы, таблицы,
формулы).).
4. Построить математическую модель задачи (составить одно
уравнение с двумя переменными и зафиксировать искомую
величину
www.sch2000.ru

27.

МАТЕМАТИЧЕСКИЙ ЯЗЫК
§ 2. Математические модели
5 класс, часть 1
I ЭТАП: ПОСТРОЕНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ
П 1. Перевод условия задачи на математический язык
Вопрос. Как комментировать процесс составления математической модели задачи,
пользуясь алгоритмом?
Задание 2. Постройте с комментированием математическую модель «Два уравнения с двумя
переменными» для задачи:
«В каждом из двух домов по 36 квартир. Во втором доме число квартир на каждом этаже на 3 меньше,
чем в первом, а число этажей — на 2 больше. Сколько этажей в каждом из этих домов?» .
В парах (2 мин) комментирует
партнер А по плечу
www.sch2000.ru

28.

5 ‒1
ПРИМЕНЯЮ НОВОЕ ЗНАНИЕ
РАБОТАЕМ В ПАРАХ
ВЫПОЛНЯЮ ПОШАГОВУЮ САМОПРОВЕРКУ
Если шаг выполнен верно, ставлю «+», если – нет , «?»
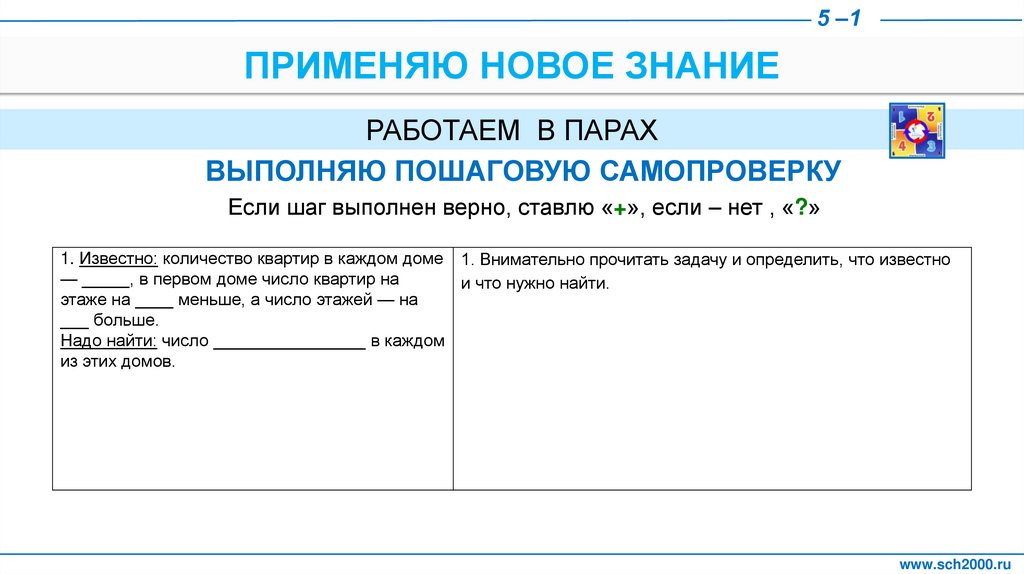
1. Известно: количество квартир в каждом доме 1. Внимательно прочитать задачу и определить, что известно
— _____, в первом доме число квартир на
и что нужно найти.
этаже на ____ меньше, а число этажей — на
___ больше.
Надо найти: число ________________ в каждом
из этих домов.
www.sch2000.ru

29.

5 ‒1
ПРИМЕНЯЮ НОВОЕ ЗНАНИЕ
РАБОТАЕМ В ПАРАХ
ВЫПОЛНЯЮ ПОШАГОВУЮ САМОПРОВЕРКУ
Если шаг выполнен верно, ставлю «+», если – нет , «?»
1. Известно: количество квартир в
1. Внимательно прочитать задачу и определить, что
каждом доме — _____, в первом доме
известно и что нужно найти.
число квартир на этаже на ____ меньше, 2. Проверить соответствие единиц счёта /
а число этажей — на ___ больше.
измерения величин (при необходимости
Надо найти: число ________________ в
выполнить их преобразование).
каждом из этих домов.
2. Единицы счёта согласованы.
www.sch2000.ru

30.

5 ‒1
ПРИМЕНЯЮ НОВОЕ ЗНАНИЕ
РАБОТАЕМ В ПАРАХ
ВЫПОЛНЯЮ ПОШАГОВУЮ САМОПРОВЕРКУ
Если шаг выполнен верно, ставлю «+», если – нет , «?»
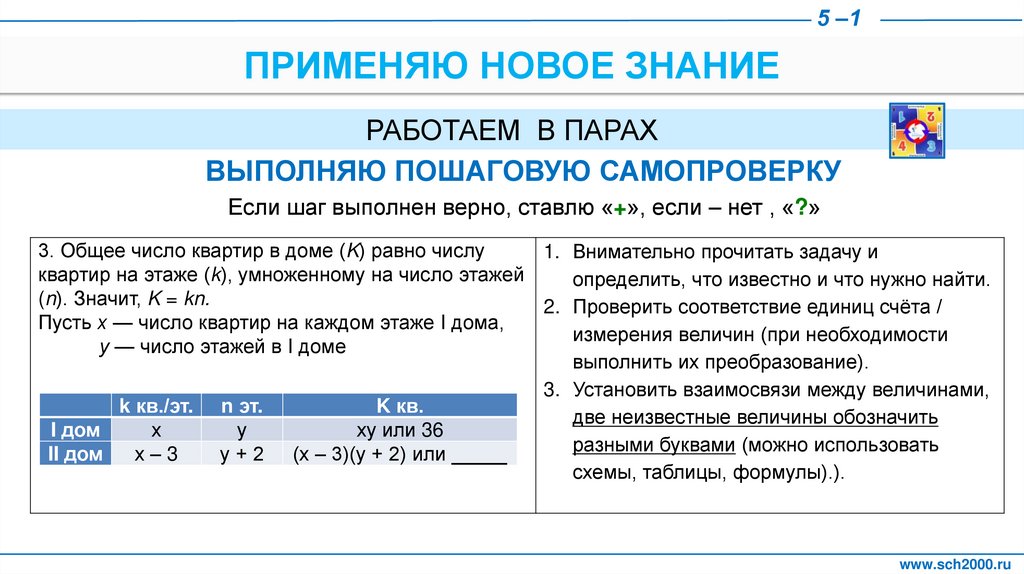
3. Общее число квартир в доме (K) равно числу
1. Внимательно прочитать задачу и
квартир на этаже (k), умноженному на число этажей
определить, что известно и что нужно найти.
(n). Значит, K = kn.
2. Проверить соответствие единиц счёта /
Пусть х — число квартир на каждом этаже I дома,
измерения величин (при необходимости
у — число этажей в I доме
выполнить их преобразование).
3. Установить взаимосвязи между величинами,
k кв./эт. n эт.
K кв.
две неизвестные величины обозначить
I дом
х
у
ху или 36
разными
буквами
(можно
использовать
II дом
х–3
у + 2 (х – 3)(у + 2) или _____
схемы, таблицы, формулы).).
www.sch2000.ru

31.

5 ‒1
ПРИМЕНЯЮ НОВОЕ ЗНАНИЕ
РАБОТАЕМ В ПАРАХ
ВЫПОЛНЯЮ ПОШАГОВУЮ САМОПРОВЕРКУ
Если шаг выполнен верно, ставлю «+», если – нет , «?»
4. Математическая модель задачи:
1) ху = ___
2) (х – 3)(у + 2) = ___
у = ? у + 2 =? (х > 3; х, y N)
1. Внимательно прочитать задачу и определить, что известно и
что нужно найти.
2. Проверить соответствие единиц счёта / измерения величин
(при необходимости выполнить их преобразование).
3. Установить взаимосвязи между величинами, две
неизвестные величины обозначить разными буквами (можно
использовать схемы, таблицы, формулы).).
4. Построить математическую модель задачи (составить два
уравнения с двумя переменными и зафиксировать
искомую
величину).
www.sch2000.ru

32.

МАТЕМАТИЧЕСКИЙ ЯЗЫК
§ 2. Математические модели
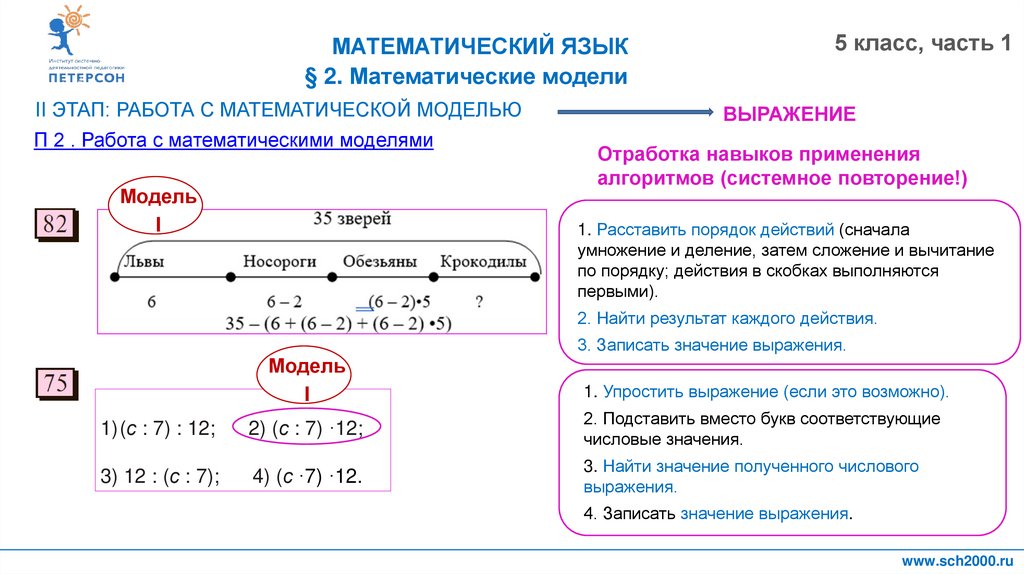
II ЭТАП: РАБОТА С МАТЕМАТИЧЕСКОЙ МОДЕЛЬЮ
П 2 . Работа с математическими моделями
Модель
I
5 класс, часть 1
ВЫРАЖЕНИЕ
Отработка навыков применения
алгоритмов (системное повторение!)
1. Расставить порядок действий (сначала
умножение и деление, затем сложение и вычитание
по порядку; действия в скобках выполняются
первыми).
2. Найти результат каждого действия.
3. Записать значение выражения.
Модель
I
1)(с : 7) : 12;
3) 12 : (с : 7);
1. Упростить выражение (если это возможно).
2) (с : 7) ·12;
2. Подставить вместо букв соответствующие
числовые значения.
4) (с ·7) ·12.
3. Найти значение полученного числового
выражения.
4. Записать значение выражения.
www.sch2000.ru

33.

МАТЕМАТИЧЕСКИЙ ЯЗЫК
§ 2. Математические модели
5 класс, часть 1
УРАВНЕНИЕ С ОДНОЙ
ПЕРЕМЕННОЙ
II ЭТАП: РАБОТА С МАТЕМАТИЧЕСКОЙ МОДЕЛЬЮ
П 2 . Работа с математическими моделями
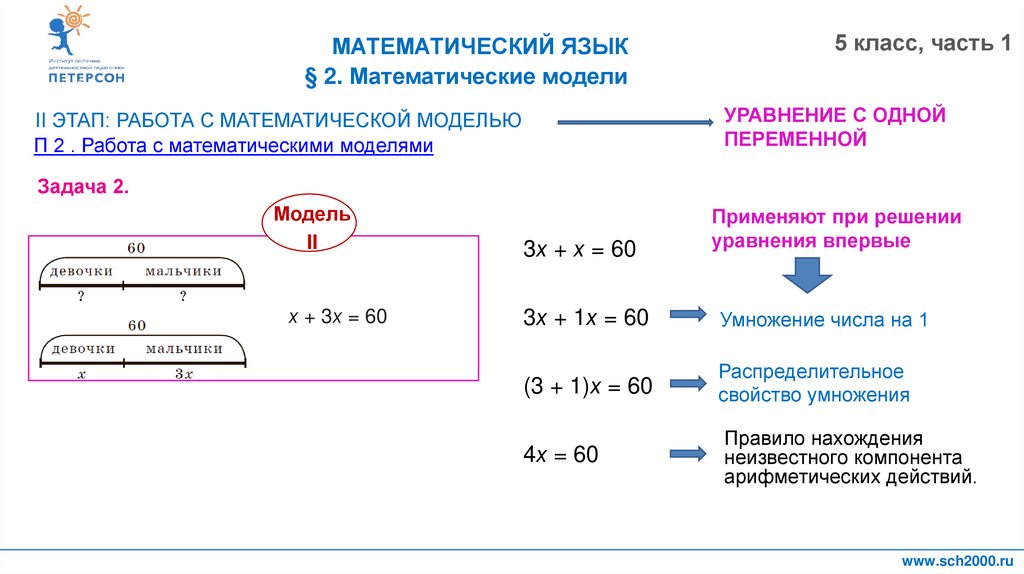
Задача 2.
Модель
II
х + 3х = 60
3х + х = 60
Применяют при решении
уравнения впервые
3х + 1х = 60
Умножение числа на 1
(3 + 1)х = 60
Распределительное
свойство умножения
4х = 60
Правило нахождения
неизвестного компонента
арифметических действий.
www.sch2000.ru

34.

МАТЕМАТИЧЕСКИЙ ЯЗЫК
§ 2. Математические модели
II ЭТАП: РАБОТА С МАТЕМАТИЧЕСКОЙ МОДЕЛЬЮ
П 2 . Работа с математическими моделями
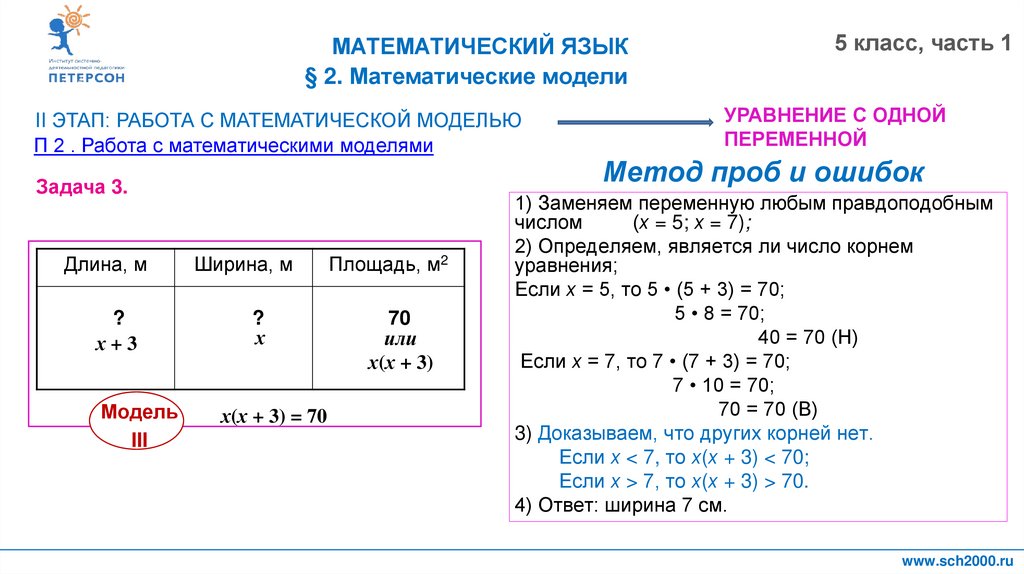
Задача 3.
Длина, м
?
х+3
Модель
III
Ширина, м
?
х
х(х + 3) = 70
Площадь, м2
70
или
х(х + 3)
5 класс, часть 1
УРАВНЕНИЕ С ОДНОЙ
ПЕРЕМЕННОЙ
Метод проб и ошибок
1) Заменяем переменную любым правдоподобным
числом
(х = 5; х = 7);
2) Определяем, является ли число корнем
уравнения;
Если х = 5, то 5 • (5 + 3) = 70;
5 • 8 = 70;
40 = 70 (Н)
Если х = 7, то 7 • (7 + 3) = 70;
7 • 10 = 70;
70 = 70 (В)
3) Доказываем, что других корней нет.
Если х < 7, то х(х + 3) < 70;
Если х > 7, то х(х + 3) > 70.
4) Ответ: ширина 7 см.
www.sch2000.ru

35.

5 класс, часть 1
МАТЕМАТИЧЕСКИЙ ЯЗЫК
§ 2. Математические модели
II ЭТАП: РАБОТА С МАТЕМАТИЧЕСКОЙ МОДЕЛЬЮ
П 2 . Работа с математическими моделями
УРАВНЕНИЕ С ОДНОЙ
ПЕРЕМЕННОЙ
Метод проб и ошибок
1. Придать переменной любое правдоподобное значение и
подставить в уравнение.
Модель
2. Если получилось верное равенство, то перейти к пункту
III
3, а если нет, то перейти к пункту 1.
х(х + 3) = 70 3. Найти тем же способом остальные корни уравнения
(если они есть) и доказать, что других корней нет.
4. Записать ответ, выписав все найденные корни.
www.sch2000.ru

36.

5 класс, часть 1
МАТЕМАТИЧЕСКИЙ ЯЗЫК
§ 2. Математические модели
ДВА УРАВНЕНИЯ С ДВУМЯ
ПЕРЕМЕННЫМ
II ЭТАП: РАБОТА С МАТЕМАТИЧЕСКОЙ МОДЕЛЬЮ
П 2 . Работа с математическими моделями
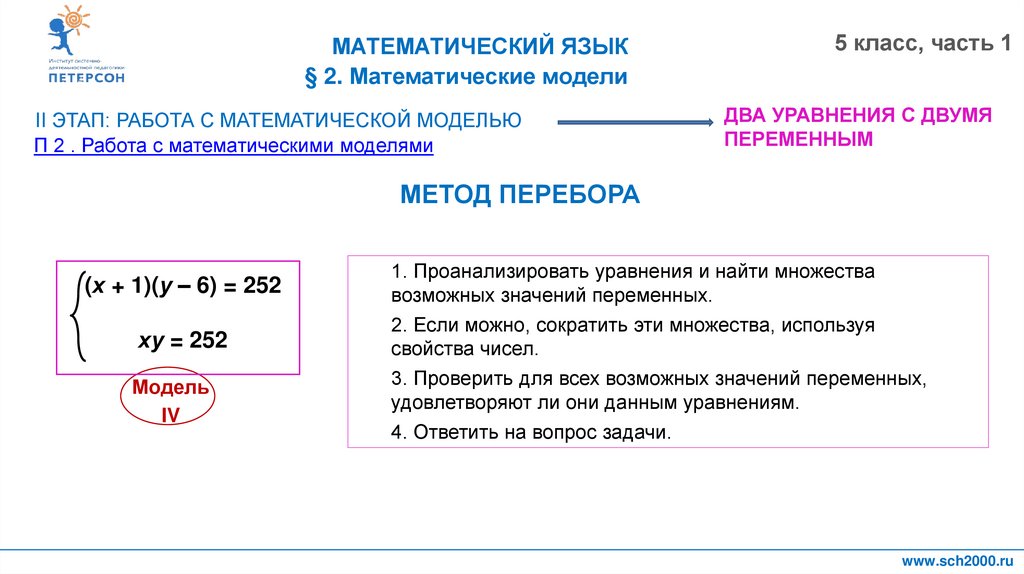
МЕТОД ПЕРЕБОРА
Задача 4.
ху = 252; (х + 1)(у – 6) = 252
Кол. д. в
одном ав., ч.
Кол. ав.,
ав.
Общее кол. ч.
Большие
автобусы
?
х
?
у
252
или
ху
Маленькие
автобусы
?
х+1
?
у-6
252
или
(х + 1)(у – 6)
х и у – парные делители 252
(х + 1)(у – 6) = 252
ху = 252
Модель
IV
х
1
2
3
4
6
7
9
14
18
28
36
у 25 126 84 63 42 36
2
28
18
14
9
7
Если х = 1, у = 252, то (1+1)(252 – 6) = 252 (Н)
Если х = 2, у = 126, то (2+ 1)(126 – 6) = 252 (Н)
Если х = 3, у = 84, то (3 + 1)(84 – 6) = 252 (Н)
Если х = 4, у = 63, то (4 + 1)(63 – 6) = 252 (Н)
Если х = 6, у = 42, то (6 + 1)(42 – 6) = 252 (В)
Если х = 9, у = 28, то (9 + 1)(28 – 6) = 252 (Н)
Если х = 14, у = 18, то (14 + 1)(18 – 6) = 252 (Н)
х = 6, у = 42
www.sch2000.ru

37.

МАТЕМАТИЧЕСКИЙ ЯЗЫК
§ 2. Математические модели
II ЭТАП: РАБОТА С МАТЕМАТИЧЕСКОЙ МОДЕЛЬЮ
П 2 . Работа с математическими моделями
5 класс, часть 1
ДВА УРАВНЕНИЯ С ДВУМЯ
ПЕРЕМЕННЫМ
МЕТОД ПЕРЕБОРА
(х + 1)(у – 6) = 252
ху = 252
Модель
IV
1. Проанализировать уравнения и найти множества
возможных значений переменных.
2. Если можно, сократить эти множества, используя
свойства чисел.
3. Проверить для всех возможных значений переменных,
удовлетворяют ли они данным уравнениям.
4. Ответить на вопрос задачи.
www.sch2000.ru

38.

5 класс, часть 1
МАТЕМАТИЧЕСКИЙ ЯЗЫК
§ 2. Математические модели
ОДНО УРАВНЕНИЕ С
ДВУМЯ ПЕРЕМЕННЫМ
II ЭТАП: РАБОТА С МАТЕМАТИЧЕСКОЙ МОДЕЛЬЮ
П 2 . Работа с математическими моделями
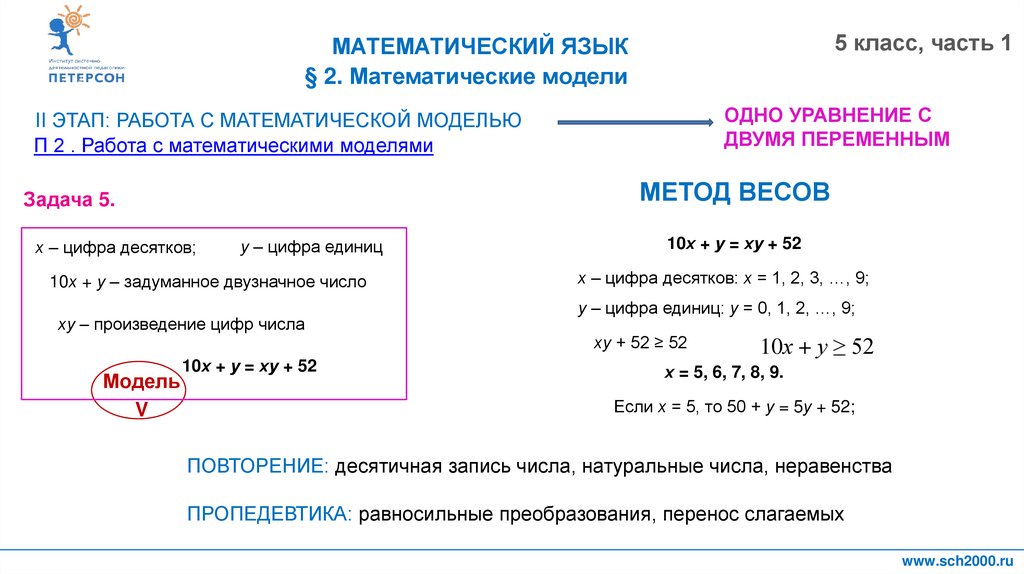
МЕТОД ВЕСОВ
Задача 5.
х – цифра десятков;
у – цифра единиц
10х + у – задуманное двузначное число
ху – произведение цифр числа
Модель
V
10х + у = ху + 52
10х + у = ху + 52
х – цифра десятков: х = 1, 2, 3, …, 9;
у – цифра единиц: у = 0, 1, 2, …, 9;
ху + 52 ≥ 52
10х + у ≥ 52
х = 5, 6, 7, 8, 9.
Если х = 5, то 50 + у = 5у + 52;
ПОВТОРЕНИЕ: десятичная запись числа, натуральные числа, неравенства
ПРОПЕДЕВТИКА: равносильные преобразования, перенос слагаемых
www.sch2000.ru

39.

5 класс, часть 1
МАТЕМАТИЧЕСКИЙ ЯЗЫК
§ 2. Математические модели
II ЭТАП: РАБОТА С МАТЕМАТИЧЕСКОЙ МОДЕЛЬЮ
П 2 . Работа с математическими моделями
ОДНО УРАВНЕНИЕ С
ДВУМЯ ПЕРЕМЕННЫМ
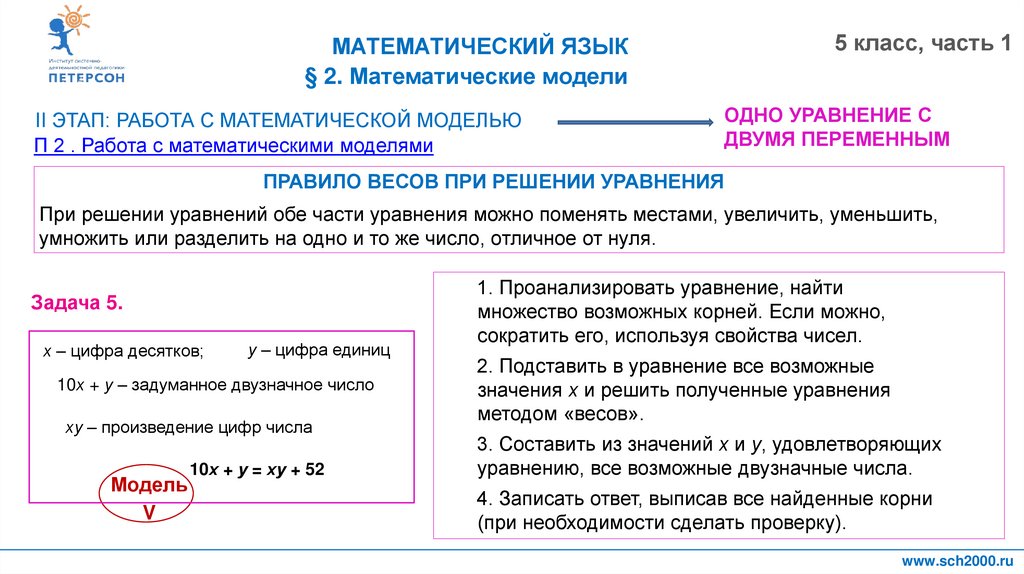
ПРАВИЛО ВЕСОВ ПРИ РЕШЕНИИ УРАВНЕНИЯ
При решении уравнений обе части уравнения можно поменять местами, увеличить, уменьшить,
умножить или разделить на одно и то же число, отличное от нуля.
Задача 5.
х – цифра десятков;
у – цифра единиц
10х + у – задуманное двузначное число
ху – произведение цифр числа
Модель
V
10х + у = ху + 52
1. Проанализировать уравнение, найти
множество возможных корней. Если можно,
сократить его, используя свойства чисел.
2. Подставить в уравнение все возможные
значения х и решить полученные уравнения
методом «весов».
3. Составить из значений х и у, удовлетворяющих
уравнению, все возможные двузначные числа.
4. Записать ответ, выписав все найденные корни
(при необходимости сделать проверку).
www.sch2000.ru

40.

МАТЕМАТИЧЕСКИЙ ЯЗЫК
§ 2. Математические модели
5 класс, часть 1
Вопрос . Из каких ключевых этапов состоит алгоритм решения задачи?
Задание 3. Заполните пропуски в алгоритме решения задач методом математического
моделирования, назвав ключевые этапы.
Методика организации
работы в группе
www.sch2000.ru

41.

МАТЕМАТИЧЕСКИЙ ЯЗЫК
§ 2. Математические модели
5 класс, часть 1
Задание 3. Заполните пропуски в алгоритме решения задач методом математического
моделирования, назвав ключевые этапы.
Алгоритм решения задач
методом математического моделирования
I. __________________________________________
1. Внимательно прочитать задачу и определить, что известно и что нужно найти.
2. Проверить соответствие единиц счёта / измерения величин (при необходимости выполнить их
преобразование).
3. Установить взаимосвязи между величинами (можно использовать схемы, таблицы, формулы). Если нужно,
одну или несколько неизвестных величин обозначить буквами.
4. Построить математическую модель задачи (выражение, уравнение и др.) и зафиксировать искомую
величину.
II. ____________________________________________
6. Найти все решения, удовлетворяющие построенной модели.
III. ____________________________________________
7. Проверить соответствие полученного ответа условию, вопросу и смыслу задачи.
www.sch2000.ru

42.

МАТЕМАТИЧЕСКИЙ ЯЗЫК
§ 2. Математические модели
5 класс, часть 1
Задание 3. Заполните пропуски в алгоритме решения задач методом математического
моделирования, назвав ключевые этапы.
ПРОВЕРЯЕМ СЕБЯ
Алгоритм решения задач
методом математического моделирования
I. Построение математической модели
1. Внимательно прочитать задачу и определить, что известно и что нужно найти.
2. Проверить соответствие единиц счёта / измерения величин (при необходимости выполнить их
преобразование).
3. Установить взаимосвязи между величинами (можно использовать схемы, таблицы, формулы). Если нужно,
одну или несколько неизвестных величин обозначить буквами.
4. Построить математическую модель задачи (выражение, уравнение и др.) и зафиксировать искомую
величину.
II. Работа с математической моделью.
6. Найти все решения, удовлетворяющие построенной модели.
III. Практический вывод.
7. Проверить соответствие полученного ответа условию, вопросу и смыслу задачи.
www.sch2000.ru

43.

Инструменты-помощники
РАБОЧАЯ ТЕТРАДЬ
НЕПРЕРЫВНОСТЬ В
МЕТОДИКЕ И ТЕХНОЛОГИИ
ВОПРОС: что дети открывают
сами?

44.

Инструменты-помощники
О непрерывности в Технологии
РАБОЧАЯ ТЕТРАДЬ
НЕПРЕРЫВНОСТЬ В
МЕТОДИКЕ И ТЕХНОЛОГИИ
ВОПРОС: что выносится на
тренинг?

45.

НОУ ДПО «Институт системно-деятельностной педагогики»
5 класс, часть 1
МАТЕМАТИЧЕСКИЙ ЯЗЫК
5 класс. Часть 1. Глава 1.
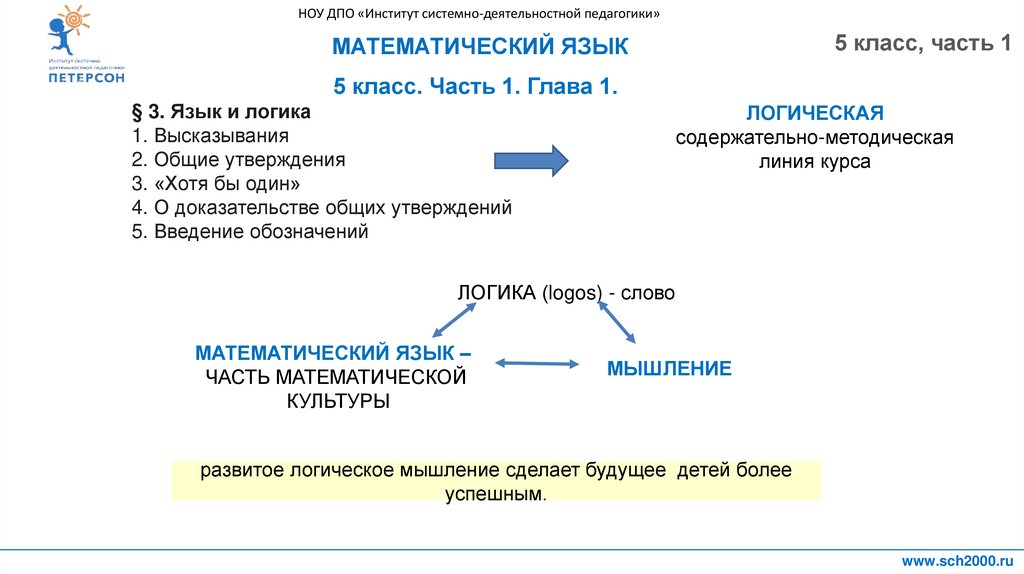
§ 3. Язык и логика
1. Высказывания.
2. Общие утверждения.
3. «Хотя бы один».
4. О доказательстве общих утверждений.
5. Введение обозначений.
ЛОГИЧЕСКАЯ
содержательно-методическая
линия курса
ЛОГИКА (logos) - слово
МАТЕМАТИЧЕСКИЙ ЯЗЫК –
ЧАСТЬ МАТЕМАТИЧЕСКОЙ
КУЛЬТУРЫ
МЫШЛЕНИЕ
развитое логическое мышление сделает будущее детей более
успешным.
www.sch2000.ru

46.

МАТЕМАТИЧЕСКИЙ ЯЗЫК
5 класс, часть 1
5 класс. Часть 1. Глава 1.
§ 3. Язык и логика
1. Высказывания.
2. Общие утверждения.
3. «Хотя бы один».
4. О доказательстве общих утверждений.
5. Введение обозначений.
ЛОГИЧЕСКАЯ
содержательно-методическая
линия курса
Содержание носит развивающий характер фон для повторения и закрепления всех остальных линий
30% (до 15 мин) урока формирование логических понятий и связанных с ними умений,
70% урока повторение и систематизация знаний и умений по основным линиям курса.
www.sch2000.ru

47.

МАТЕМАТИЧЕСКИЙ ЯЗЫК
5 класс, часть 1
5 класс. Часть 1. Глава 1.
§ 3. Язык и логика
ЛОГИЧЕСКАЯ
1. Высказывания.
содержательно-методическая
2. Общие утверждения.
линия курса
3. «Хотя бы один».
4. О доказательстве общих утверждений.
5. Введение обозначений.
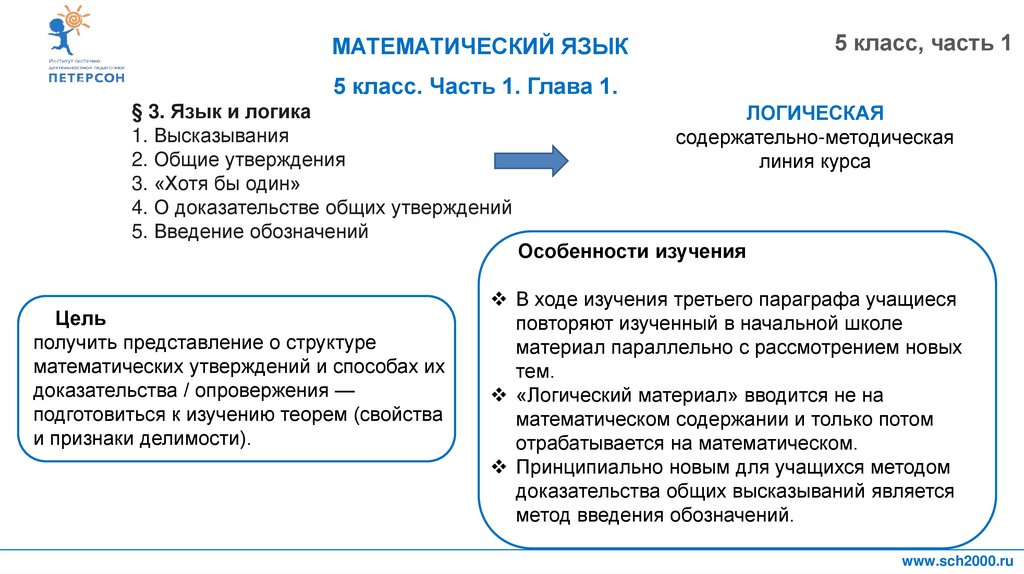
Особенности изучения
Цель
получить представление о структуре
математических утверждений и способах их
доказательства / опровержения —
подготовиться к изучению теорем (свойства
и признаки делимости).
В ходе изучения третьего параграфа учащиеся
повторяют изученный в начальной школе
материал параллельно с рассмотрением новых
тем.
«Логический материал» вводится не на
математическом содержании и только потом
отрабатывается на математическом.
Принципиально новым для учащихся методом
доказательства общих высказываний является
метод введения обозначений.
www.sch2000.ru

48.

МАТЕМАТИЧЕСКИЙ ЯЗЫК
5 класс, часть 1
5 класс. Часть 1. Глава 1.
§ 3. Язык и логика
ЛОГИЧЕСКАЯ
1. Высказывания.
содержательно-методическая
2. Общие утверждения.
линия курса
3. «Хотя бы один».
4. О доказательстве общих утверждений.
5. Введение обозначений.
анализ, синтез, сравнение, обобщение, аналогия, классификация
КЛАСС
1 класс,
ТЕМА
Тренинг мыслительных операций: анализ, сравнение, обобщение, классификация и др.
Верно и неверно.
2 класс
3 класс,
4 класс
Формирование представлений о доказательстве как ссылке на согласованное правило.
Решение логических задач.
Множество, элемент, диаграмма Венна. Подмножество, объединение, пересечение,
сложение и вычитание множеств. Знаки , , , , .
Понятие высказывания. Высказывания с союзами «и» и «или».
www.sch2000.ru

49.

МАТЕМАТИЧЕСКИЙ ЯЗЫК
5 класс, часть 1
5 класс. Часть 1. Глава 1.
§ 3. Язык и логика
1. Высказывания.
2. Общие утверждения.
3. «Хотя бы один».
4. О доказательстве общих утверждений.
5. Введение обозначений.
5 класс
ЛОГИЧЕСКАЯ
содержательно-методическая
линия курса
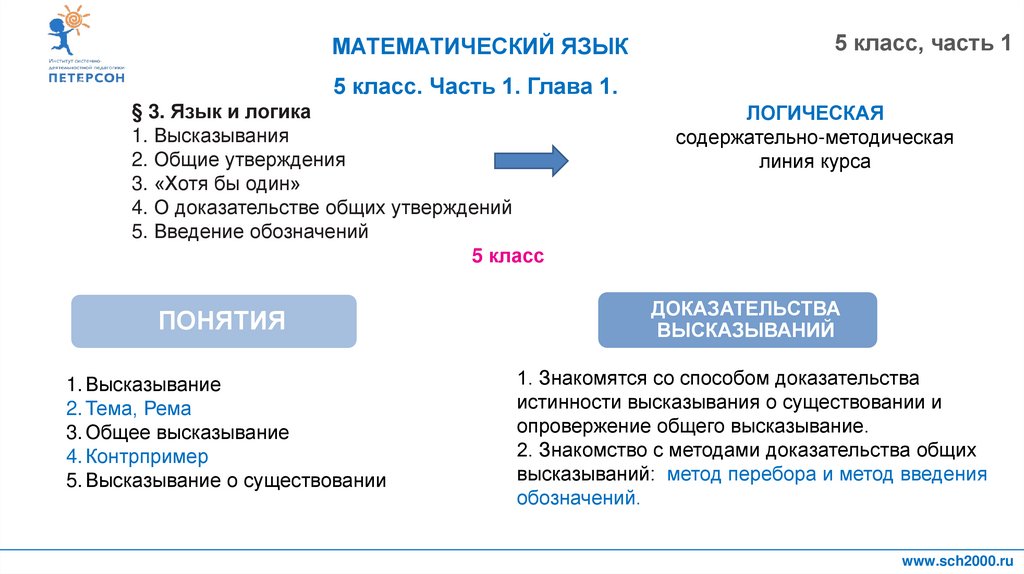
ПОНЯТИЯ
ДОКАЗАТЕЛЬСТВА
ВЫСКАЗЫВАНИЙ
1. Высказывание
2. Тема, Рема
3. Общее высказывание
4. Контрпример
5. Высказывание о существовании
1. Знакомятся со способом доказательства
истинности высказывания о существовании и
опровержение общего высказывание.
2. Знакомство с методами доказательства общих
высказываний: метод перебора и метод введения
обозначений.
www.sch2000.ru

50.

5 класс, часть 1
МАТЕМАТИЧЕСКИЙ ЯЗЫК
5 класс. Часть 1. Глава 1.
§ 3. Язык и логика
1. Высказывания.
2. Общие утверждения.
3. «Хотя бы один».
4. О доказательстве общих утверждений.
5. Введение обозначений.
ЛОГИЧЕСКАЯ
содержательно-методическая
линия курса
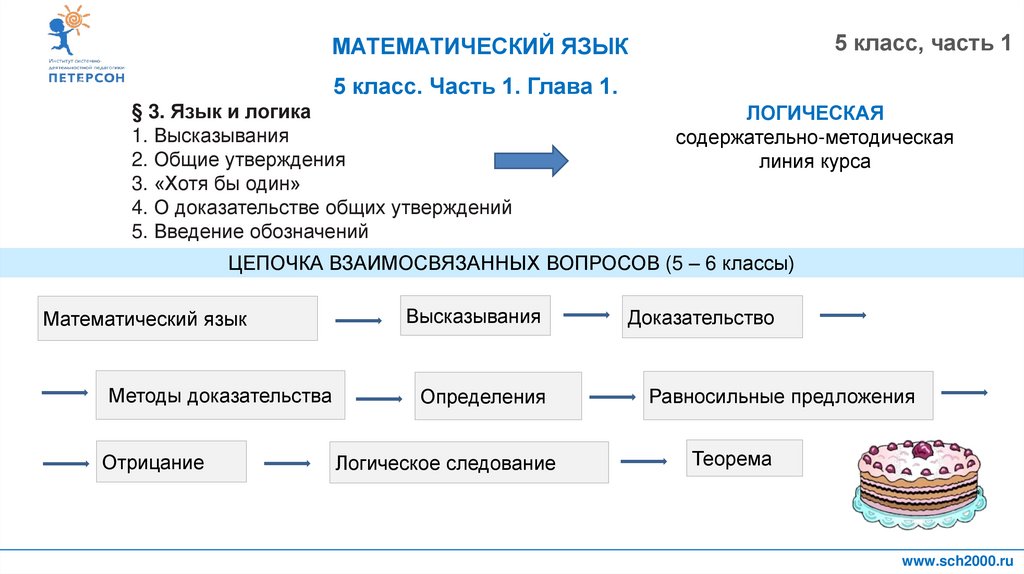
ЦЕПОЧКА ВЗАИМОСВЯЗАННЫХ ВОПРОСОВ (5 – 6 классы)
Математический язык
Методы доказательства
Отрицание
Высказывания
Определения
Логическое следование
Доказательство
Равносильные предложения
Теорема
www.sch2000.ru

51.

МАТЕМАТИЧЕСКИЙ ЯЗЫК
§ 3. Язык и логика
НЕ МАТЕМАТИКА
5 класс, часть 1
МАТЕМАТИКА + СИСТЕМНОЕ ПОВТОРЕНИЕ
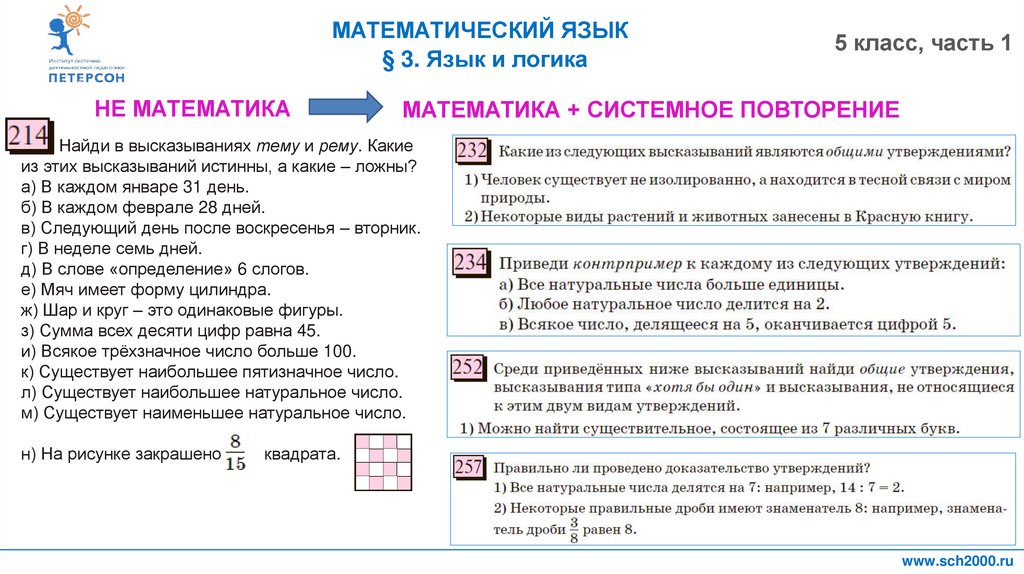
Найди в высказываниях тему и рему. Какие
из этих высказываний истинны, а какие – ложны?
а) В каждом январе 31 день.
б) В каждом феврале 28 дней.
в) Следующий день после воскресенья – вторник.
г) В неделе семь дней.
д) В слове «определение» 6 слогов.
е) Мяч имеет форму цилиндра.
ж) Шар и круг – это одинаковые фигуры.
з) Сумма всех десяти цифр равна 45.
и) Всякое трёхзначное число больше 100.
к) Существует наибольшее пятизначное число.
л) Существует наибольшее натуральное число.
м) Существует наименьшее натуральное число.
н) На рисунке закрашено
квадрата.
www.sch2000.ru

52.

МАТЕМАТИЧЕСКИЙ ЯЗЫК
§ 3. Язык и логика
опора на житейский опыт
5 класс, часть 1
Задание на пробное действие.
Доказать утверждение:
«Все числа из множества
{5, 10, 15, 20, 25, 30} делятся на 5».
www.sch2000.ru

53.

МАТЕМАТИЧЕСКИЙ ЯЗЫК
§ 3. Язык и логика
Обобщение
накопленного
опыта
5 класс, часть 1
Пропедевтика доказательства
свойств делимости
ПРИНЦИПИАЛЬНО НОВЫЙ МЕТОД ДОКАЗАТЕЛЬСТВА
www.sch2000.ru

54.

МАТЕМАТИЧЕСКИЙ ЯЗЫК
5 класс, часть 1
§ 3. Язык и логика
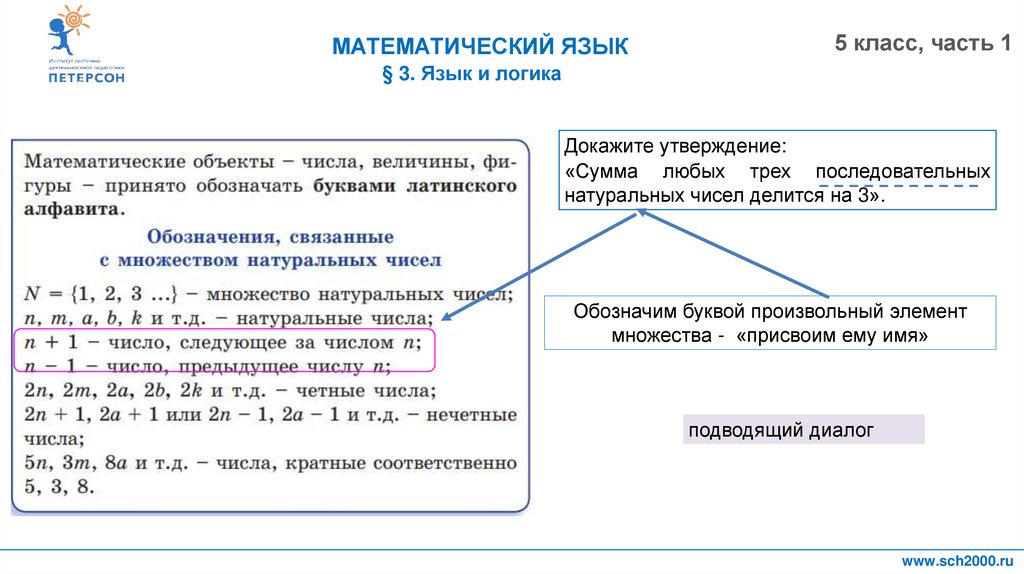
Докажите утверждение:
«Сумма любых трех последовательных
натуральных чисел делится на 3».
Обозначим буквой произвольный элемент
множества - «присвоим ему имя»
подводящий диалог
www.sch2000.ru

55.

МАТЕМАТИЧЕСКИЙ ЯЗЫК
5 класс, часть 1
§ 3. Язык и логика
Задание 6. Попробуйте прокомментировать
доказательство общего утверждения методом
введения обозначений.
Методика организации
работы в группе
www.sch2000.ru

56.

5 класс, часть 1
МАТЕМАТИЧЕСКИЙ ЯЗЫК
§ 3. Язык и логика
ПРОВЕРЯЕМ СЕБЯ
Введём обозначение: обозначим натуральное число буквой n.
Надо
записать
сумму
натуральных чисел.
пяти
последовательных
Построим математическую модель:
n + (n + 1) + (n + 2) + (n + 3) + (n + 4)
Упростить
выражение,
используя
сочетательное,
переместительное свойства сложения: 5n + 10
Записать сумму в виде произведения, используя
распределительное свойство: 5n + 5 2 = 5(n+ 2).
Число представлено в виде произведения, значит, оно
делится на каждый множитель, делится на 5.
Ответ: делится.
www.sch2000.ru

57.

МАТЕМАТИЧЕСКИЙ ЯЗЫК
5 класс, часть 1
Задание 4. (В парах, группах)
Выяснить в парах, какие темы повторяются, согласовать ответ в
группах, проверить себя, обозначить смысл повторения.
Вынести на обсуждение согласованные от группы варианты
www.sch2000.ru

58.

МАТЕМАТИЧЕСКИЙ ЯЗЫК
5 класс, часть 1
РЕФЛЕКСИЯ
Задание 5.
Заполнить карту рефлексии
Заполнить стикеры, согласовав ответы в группах:
синий – что уточнили для себя, что стало новым знанием (в содержании,
методике или в технологии);
зеленый – какие вопросы остались.
www.sch2000.ru