Похожие презентации:
Динамика материальной точки и поступательного движения твердого тела
1. Динамика материальной точки и поступательного движения твердого тела
Динамика- основной раздел механики,в её основе лежат 3 закона Ньютона
(1687 г.), рассматриваемые как система
взаимосвязанных законов.
2. Первый закон Ньютона (закон инерции)
Всякая материальная точка (тело) сохраняетсостояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит её
изменить это состояние.
3. ИНЕРТНОСТЬ, МАССА, СИЛА
• Инертность- стремление тела сохранить своёсостояние покоя или равномерного прямолинейного движения (1 закон Ньютона называют закон инерции ).
• Инерциальная система отсчёта – система, которая либо покоится, либо движется прямолинейно и равномерно относительно какойлибо другой инерциальной системы отсчёта.
1 закон Ньютона выполняется не в каждой, а
только в инерциальных системах отсчёта.
4.
• Масса- физическая величина, являющаяся одной из характеристик материи, определяющаяеё инерционные и гравитационные свойства.
• Сила – векторная величина, являющаяся мерой механического воздействия на тело со
стороны других тел и полей, в результате
которого тело приобретает ускорение или изменяет свою форму и размеры. В каждый момент времени сила характеризуется числовым
значением, направлением в пространстве и
точкой приложения. Единица измерения силы
Ньютон (Н):
1Н=1 кг∙м/с²
5. Второй закон Ньютона (основной закон динамики поступательного движения)
Ускорение приобретаемое материальнойточкой (телом) пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе
материальной точки (тела).
d d
F ma m
m
dt dt
6. Импульс
Импульс (количество движения)-векторнаявеличина численно равная произведению массы материальной точки на её скорость и
имеющая направление скорости.
p m
Общая формулировка второго закона Ньютона:
Скорость изменения импульса равна действующей на него силе
dp
F
dt
7.
• Второй закон Ньютона справедлив только винерциальных системах отсчета.
• Первый закон Ньютона можно
вывести
из
второго закона Ньютона ( F 0 a 0). Однако,
первый закон Ньютона - самостоятельный
закон, а не следствие второго закона Ньютона, т. к. именно он подтверждает существование инерциальных систем отсчёта, только в
которых возможно равенство
dp
F
dt
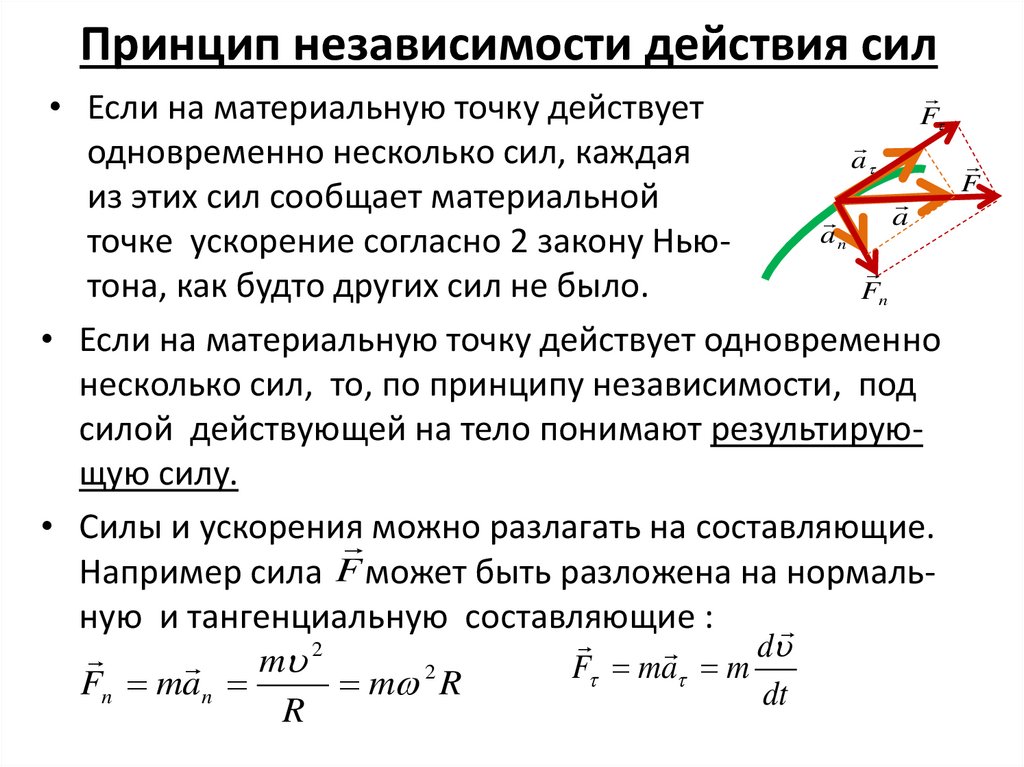
8. Принцип независимости действия сил
• Если на материальную точку действуетF
одновременно несколько сил, каждая
a
из этих сил сообщает материальной
a
a
точке ускорение согласно 2 закону Нью
тона, как будто других сил не было.
Fn
• Если на материальную точку действует одновременно
несколько сил, то, по принципу независимости, под
силой действующей на тело понимают результирующую силу.
• Силы и ускорения
можно разлагать на составляющие.
Например сила F может быть разложена на нормальную и тангенциальную составляющие :
d
m 2
F ma m
Fn ma n
m 2 R
dt
R
n
F
9. Третий закон Ньютона
Всякое действие материальных точек (тел)друг на друга носит характер взаимодействия , силы, с которыми действуют друг на
друга материальные точки, всегда равны по
модулю, противоположно направлены и
действуют вдоль прямой соединяющей эти
точки.
F12 F21
10.
F12- сила действующая на первую
F12
F21
материальную
точку со стороны
второй, а F21 на вторую точку со
2
1
стороны первой.
• Силы F12 и F21приложены к разным материальным
точкам (телам), всегда действуют парами, и являются
силами одной природы.
• Во 2 законе Ньютона речь идёт об ускорении приобретаемом телом под действием приложенных к нему
сил. Ускорение равно 0, если нулю равна равнодействующая всех сил приложенных к ОДНОМУ телу. 3 закон
Ньютона говорит о равенстве сил приложенных к
РАЗНЫМ телам. На каждое тело действует ОДНА сила.
• 3 закон Ньютона позволяет перейти от динамики одной
материальной точки к динамике системы мат. точек.
11. Законы Кеплера. Закон всемирного тяготения. Сила тяжести. Вес.
12. Законы движения планет
1. Каждая планета движется по эллипсу, в одном из фокусов которого находится Солнце.2. Радиус-вектор планеты за равные промежутки времени описывает равные площади.
3. Квадраты периодов обращения планет вокруг Солнца относятся как кубы больших осей
их полуорбит.
Законы выведены Кеплером, на основе записей Т. Браге. Впоследствии Ньютон на основании законов Кеплера и основных законов
динамики вывел:
13. Закон всемирного тяготения
Между любыми двумя материальными точками действует сила взаимного притяженияпрямо пропорциональная произведению
масс m1 и m2 этих точек, и обратно пропорциональная квадрату расстояния r между
ними.
(сила всемирного тяготения)
m1 m2
F G
r2
14. Гравитационная постоянная
G 6,6720 1011
2
Hì
êã2
Смысл гравитационной постоянной G:
Два тела массами m₁=m₂=1 кг на расстоянии r=1 м притягиваются друг к другу с силой F=6,6720∙10¯¹¹ Н.
15. Сила тяжести
На любое тело массой m , вблизи Землидействует сила тяготения F.
Силой тяжести материальной точки называют
силу Р, равную векторной разности между силой F
тяготения этой материальной точки к Земле и
центростремительной силой Fц, обусловливающей
участие материальной точки в суточном вращении
Земли. Под действием только силы тяжести тело
будет двигаться с ускорением свободного падения g≈9,81 м/с². Таким образом, на всякое тело m
действует сила тяжести
Ð mg
16. Обобщенный закон Галилея
Все тела в одном и том же поле тяготенияпадают с одинаковым ускорением.
(ускорение незначительно варьируется от
радиуса Земли)
17. Вес тела
• Вес тела – сила, с которой это тело действуетвследствие тяготения к Земле на опору (или
подвес), удерживающую тело от свободного
падения.
• Вес тела проявляется только в том случае, если
тело двигается с ускорением отличным от g т.е.
когда на тело действуют и другие силы.
• Если тело двигается только под действием силы
тяжести, то оно находится в состоянии невесомости.
18. Сила тяжести действует ВСЕГДА, вес появляется только в том случае, когда на тело кроме силы тяжести действуют и ДРУГИЕ силы
Тело двигается с ускорением a отличным от g. Еслитело двигается в поле тяготения Земли с ускорением
а g то к телу приложена дополнительная
сила N
удовлетворяющая условию N P ma
Тогда вес тела P N P ma mg ma m g a
Если тело покоится или
прямолинейно и
двигается
равномерно а 0 и P mg .
Если тело свободно двигается в любом направлении
по любой траектории то а g и P 0 т.е. тело будет
невесомым.
19. Сила трения
• Сила трения препятствуют скольжениюсоприкасающихся тел относительно друг
друга.
• Силы трения зависят от относительных скоростей тел.
• Силы трения могут быть различной природы. Но в результате их действия механическая энергия всегда превращается во внутреннюю энергию соприкасающихся тел.
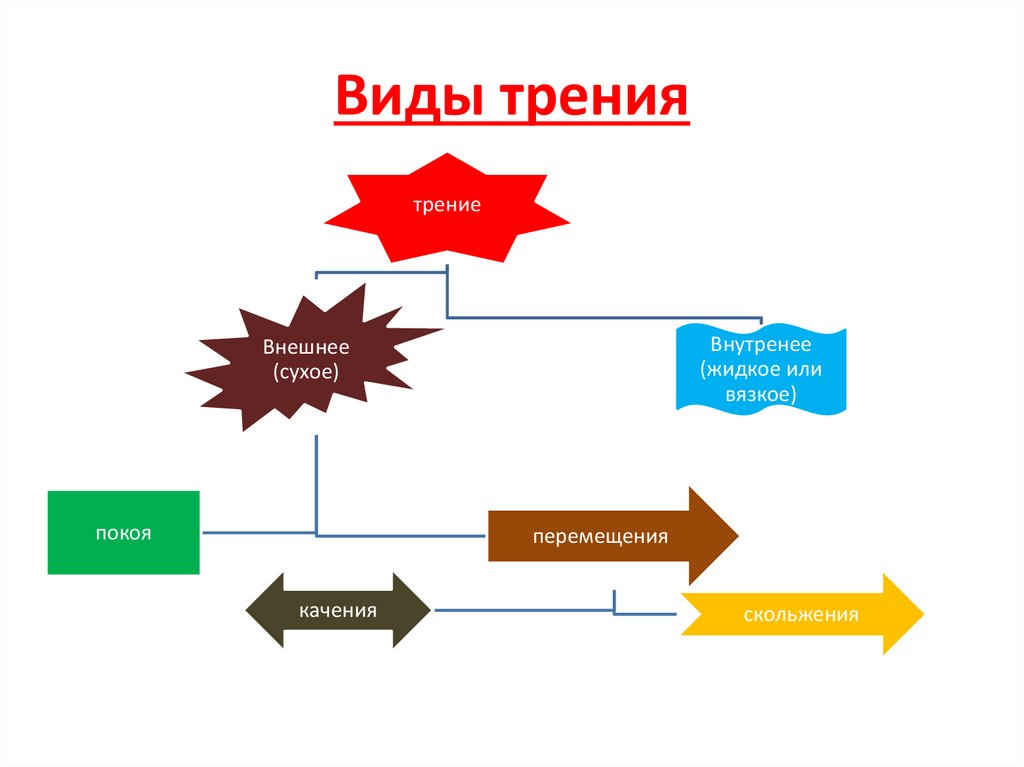
20. Виды трения
трениеВнутренее
(жидкое или
вязкое)
Внешнее
(сухое)
покоя
перемещения
качения
скольжения
21.
• Трение внешнее (сухое)-возникает в области касаниядвух соприкасающихся тел при их относительном перемещении. Если соприкасающиеся тела неподвижнытрение покоя. Если происходит относительное перемещение этих тел, то в зависимости от характера их относительного движения- трение скольжения, качения .
• Трение внутреннее- трение между частями одного и того же тела, например между слоями жидкости или газа,
скорости которых меняются от слоя к слою. В данном
случае отсутствует трение покоя.
• Если тела скользят относительно друг друга и разделены прослойкой вязкой жидкости – граничное трение
(толщина смазки h = 1 мкм) или гидродинамическое
трение (толстый слой смазки).
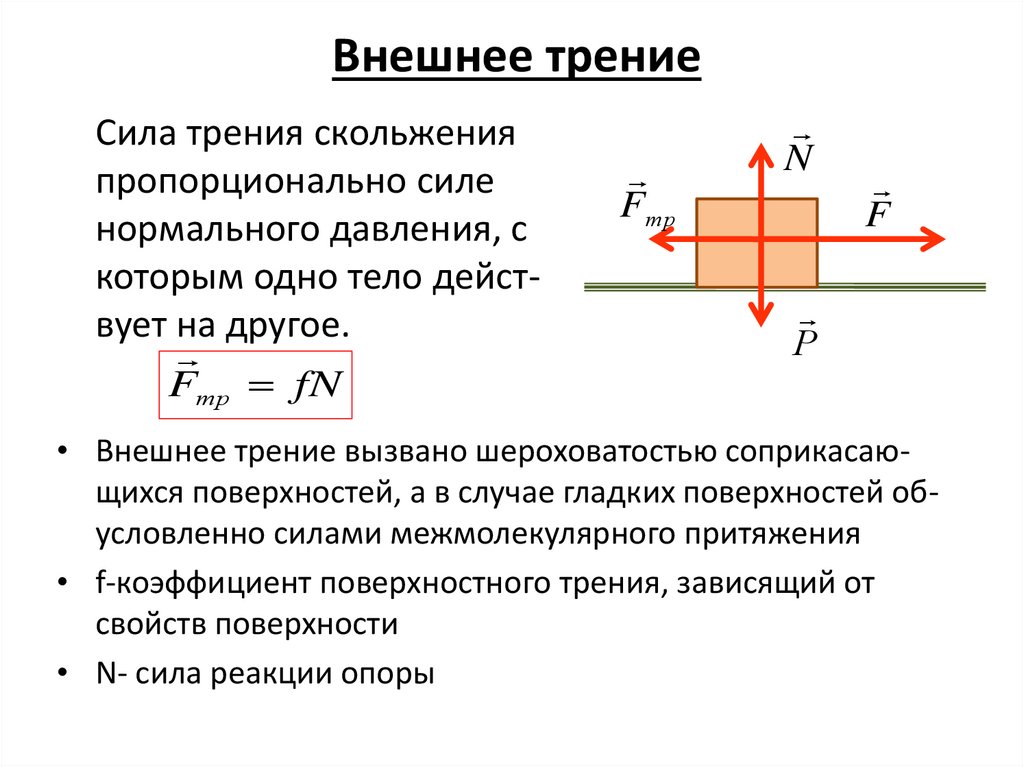
22. Внешнее трение
Сила трения скольженияпропорционально силе
нормального давления, с
которым одно тело действует на другое.
Fтр fN
Fтр
N
F
Р
• Внешнее трение вызвано шероховатостью соприкасающихся поверхностей, а в случае гладких поверхностей обусловленно силами межмолекулярного притяжения
• f-коэффициент поверхностного трения, зависящий от
свойств поверхности
• N- сила реакции опоры
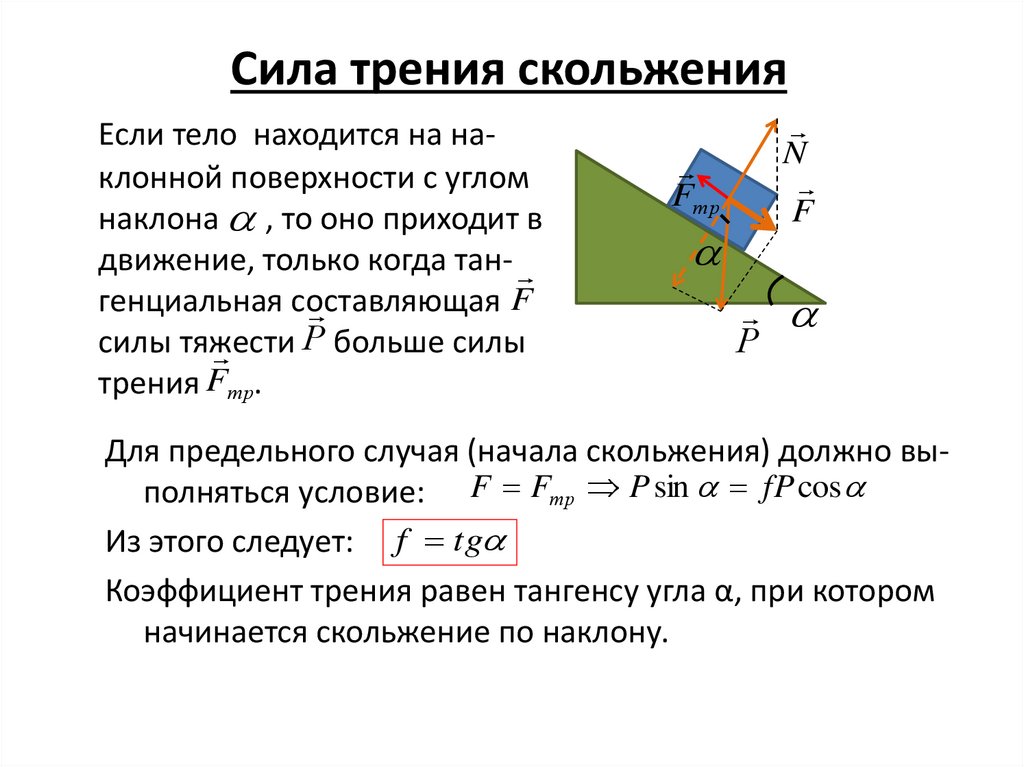
23. Сила трения скольжения
Если тело находится на наклонной поверхности с угломнаклона , то оно приходит в
движение, только когда тан-
F
генциальная составляющая
Р больше силы
силы тяжести
трения Fтр.
Fтр
N
F
Р
Для предельного случая (начала скольжения) должно выполняться условие: F Fтр P sin fP cos
Из этого следует: f tg
Коэффициент трения равен тангенсу угла α, при котором
начинается скольжение по наклону.
24.
• Для трения скольжения на гладких поверхностях определённую роль играет межмолекулярное притяжение.Закон трения скольжения (предложен Б.В. Дерябиным)
Fтр f ист N SP0
где:
f ист -истинный коэффициент трения скольжения
-площадь контакта между телами
S
Р0 -добавочное давление обусловленное силами межмолекулярного притяжения
• Сила трения качения (по закону Кулона)
Fтр f к N
r
где:
f к -коэффициент трения качения
r -радиус катящегося тела
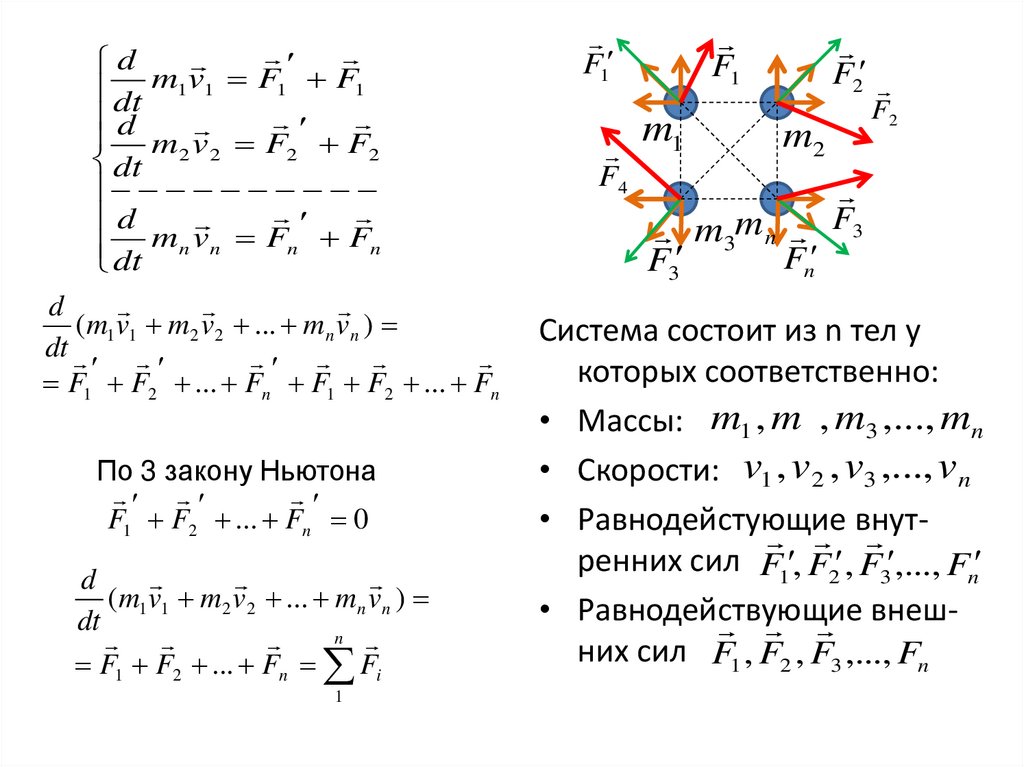
25. Закон сохранения импульса
26.
• Механическая система-совокупность материальных точек (тел) рассматриваемых какединое целое.
• Внутренние силы- силы взаимодействия между материальными точками механической
системы.
• Внешние силы- силы, с которыми на материальные точки системы действуют внешние
тела.
• Замкнутая система- система, на которую не
действуют внешние силы, или геометрическая
сумма всех внешних сил равна нулю.
27.
ddt m1v1 F1 F1
d
m2 v 2 F2 F2
dt
d
mn v n Fn Fn
dt
d
(m1v1 m2 v 2 ... mn v n )
dt
F1 F2 ... Fn F1 F2 ... Fn
По 3 закону Ньютона
F1 F2 ... Fn 0
d
(m1v1 m2 v 2 ... mn v n )
dt
n
F1 F2 ... Fn Fi
1
F1
F1
F4
m1
F2
m2
F2
m3m n F3
Fn
F3
Система состоит из n тел у
которых соответственно:
• Массы: m1 , m , m3 ,..., mn
• Скорости: v1 , v 2 , v3 ,..., v n
• Равнодейстующие
внут
ренних сил F1 , F2 , F3 ,..., Fn
• Равнодействующие
внешних сил F1 , F2 , F3 ,..., Fn
28.
Так как по 3 закону Ньютона геометрическая сумма внутренних сил равна нулю F1 F2 ... Fn 0 то:
n
d
dp
(m1v1 m2 v 2 ... mn v n ) F1 F2 ... Fn Fi
dt
dt
1
n
где: p mi vi
-импульс системы.
1
Производная по времени импульса механической системы равна геометрической сумме внешних сил действующих на систему.
В случае отсутствия внешних сил (система замкнутая)
n
n
dp
mi ai Fi 0
dt
1
i
29. Закон сохранения импульса
Импульс замкнутой системы не изменяется стечением времени.
n
p mi vi const
1
Данный закон справедлив не только для классической механики, он носит универсальный
характер, то есть он: УНИВЕРСАЛЬНЫЙ
ЗАКОН ПРИРОДЫ.
30. Центр масс
• В механике Галилея-Ньютона импульс системы из-за независимости массы от скорости может быть выражен через скоростьеё центра масс.
• Центром масс (центром инерции)- для системы материальных точек называется воображаемая точка С положение которой
характеризует распределение массы всей
системы.
31.
mi rin
• Радиус-вектор центра масс:
rc 1
Где:
m
mi ri -масса и радиус вектор ¡-ой материальной точки
n -число материальных точек в системе
m -масса всей системы
n
n
d
r
• Скорость центра масс:
i
d
r
vc c
dt
p
n
1
pi
m
i
1
m
dt
m v
mi vi mvc
n
1
• Импульс системы равен произведению массы
системы на скорость её центра масс.
p mvc
i
1
m
i
32. Закон движения центра масс
Центр масс системы двигается как материальная точка, в которой сосредоточена вся масса системы, и на которую действует силаравная геометрической сумме всех внешних
сил, действующих
на систему.
dvc
m
F1 F2 ... Fn
dt
Центр масс замкнутой системы либо движется
прямолинейно и равномерно, либо остаётся
неподвижным.
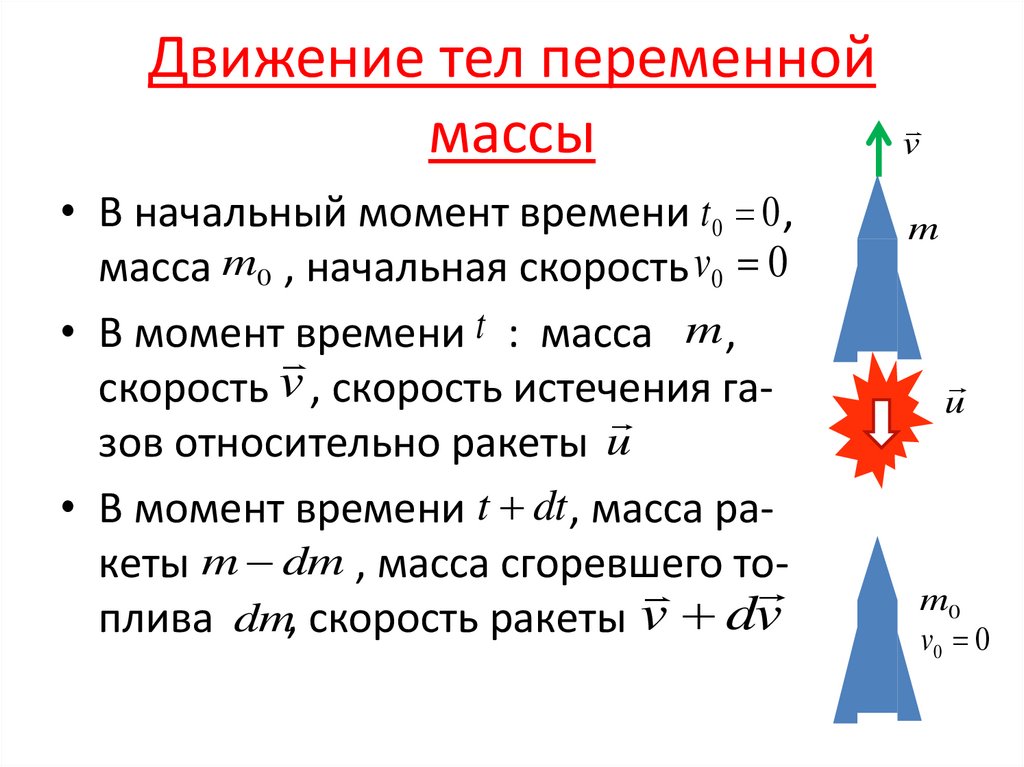
33. Движение тел переменной массы
• В начальный момент времени t 0 0 ,масса m0 , начальная скорость v0 0
• В момент времени t : масса m ,
скорость v , скорость истечения га
зов относительно ракеты u
• В момент времени t dt , масса ракеты m dm , масса сгоревшего то
плива dm, скорость ракеты v dv
v
m
u
m0
v0 0
34.
Изменение импульса системы за время dt:dp m dm v dv dm v u mv mdv udm
Если на тело действуют внешние силы то :
dp Fdt Fdt mdv udm
dm
dv
m
F u
dt
dt
dm
F p -реактивная сила
где : u
dt
Если u противоположно по направлению с v
то ракета разгоняется, если совпадает то
тормозится.
35. Уравнение движения тела переменной массы
ma F Fp(Уравнение Мещерского)
Если на движущуюся ракету не действуют внешние
силы (F=0) и скорость выбрасываемых газов
постоянна
то:
dv
dm
dm
m
u
v u
u ln m C
dt
dt
m
Значение постоянной интегрирования С определим из
начальных условий. Если v0 0 и m m0то
C u ln m0
Следовательно:
36. Формула Циолковского
m0v u ln(
)
m
Формула Циолковского показывает:
• Чем больше конечная масса ракеты (m),
тем больше должна быть стартовая масса
ракеты (m0).
• Чем больше скорость истечения газов (u),
тем больше может быть конечная масса (m)
при данной стартовой массе (m0) ракеты.






























 Физика
Физика








