Похожие презентации:
Курс лекций по сопротивлению материалов. Часть 2.1
1. Курс лекций по сопротивлению материалов
Московский государственный университет путей сообщения (МИИТ)Кафедра строительной механики
Научно-технический центр транспортных технологий
Бондаренко А.Н.
y
y
z
dz
dφ
x
z
Курс лекций по
сопротивлению
материалов
v=v(z)
φ
θ=φ
Часть 2.1
Электронный учебный курс написан на основе лекций, читавшихся автором для студентов,
обучавшихся по специальностям СЖД, ПГС и СДМ в ХабИИЖТе, СГУПСе (1965-2003 гг.).
Учебный материал соответствует календарным планам в объеме двух семестров.
Для полной реализации анимационных эффектов при презентации необходимо использовать средство просмотра
Power Point не ниже, чем встроенный в Microsoft Office операционной системы Windows-ХР Professional. Запуск
презентации – F5, навигация – Enter, навигационные клавиши, щелчок мыши, кнопки.
Завершение – Esc.
Замечания и предложения можно послать по e-mail: bond@miit.ru .
Москва - 2007
2. Содержание
Лекция 1. Перемещения при изгибе. Основные допущения. Дифференциальные уравнения изогнутойоси балки и его интегрирование.
Лекция 2. Метод начальных параметров. Универсальные формулы для определения прогибов и углов
поворота поперечных сечений.
Лекция 3. Принцип возможных перемещений и его использование при расчете деформируемых
систем. Формула Максвелла-Мора.
Лекция 4. Способы вычисления интеграла Мора: непосредственное интегрирование, способ
Верещагина, формулы трапеций и Симпсона.
Лекция 5. Основы расчета статически неопределимых балок по методу сил. Степень статической
неопределимости, основная система, уравнения совместности деформаций.
Лекция 6. Сложное сопротивление. Построение эпюр внутренних усилий в пространственном
ломанном стержне.
Лекция 7. Одновременное действие продольной силы и изгибающих моментов. Определение
нормальных напряжений и положения нулевой линии. Косой изгиб.
Лекция 8. Внецентренное действие силы. Понятие о ядре сечения. Изгиб с кручением. Определение
перемещений в пространственном стержне.
Лекция 9. Общие понятия о теориях прочности. Критерий разрушения путем отрыва (хрупкое
разрушение). Краткие сведения от первой и второй теориях прочности. Теория прочности Мора.
Лекция 10. Критерий пластического состояния. Третья и четвертая теории прочности. Оценка прочности
с применением теорий прочности. Понятия о новых теориях прочности и механики разрушения.
Рекомендуемая литература
1. Александров А.В., Потапов В.Д., Державин Б.П. Сопротивление материалов для вузов. М.: Высшая школа. 1995,
2001 г. 560 с.
2. Сборник задач по сопротивлению материалов под ред. Александрова А.В., М.: Стройиздат. 1977г. 335 с.
3. Методические указания к выполнению расчетно-графических работ. Изд. МИИТ.
4. Лабораторные работы по сопротивлению материалов (Методические указания под ред. Александрова А.В.,
часть 1, МИИТ, 1974 г.)
5. Справочник по сопротивлению материалов / Писаренко Г.С., Яковлев А.П., Матвеев В.В. - 2 изд., перераб. и доп.
– Киев: Наукова думка, 1988. 736 с.
3. Лекция 1
1.2.
3.
Перемещения при изгибе – При изгибе ось балки искривляется (прогибается) в результате деформаций каждого элемента балки
длиной dz, при которых смежные сечения поворачиваются относительно друг друга на угол dφ. При поперечном изгибе элемент
испытывает дополнительные сдвиговые деформации, также изменяющие положение центра тяжести сечения относительно исходной
осевой линии. В общем случае ось балки искривляется по кривой с уравнением v = v(z). Эта кривая называется упругой линией или
линией прогибов.
Основные допущения –
Прогибы малы.
Влияние деформаций сдвига на величину прогиба пренебрежимо мало.
При прогибе балки центр тяжести поперечного сечения перемещается перпендикулярно первоначальной оси балки в направлении
главной оси сечения (y).
Поскольку влиянием деформаций сдвига пренебрегается, то каждое сечение согласно гипотезе плоских сечений при изгибе остается
нормальным к оси изогнутого стержня (упругой линии). Отсюда угол наклона сечения равен углу наклона θ касательной к упругой оси.
y
Тангенс угла наклона касательной, как известно, определяется
y
dφ
dz
как производная от уравнения кривой (см. геометрический смысл
x
z
z
производной):
dv
tg
dz
.
По малости прогибов и,
dv
tg .
следовательно,
малости
углов:
θ=φ
dz
φ
В итоге, угол поворота поперечного сечения
dv
определяется производной по координате z от функции прогибов :
.
dz
Дифференциальное уравнение прогибов – При выводе формулы нормальных напряжений была получена формула
d2y
для радиуса кривизны
1 Mx
Радиус кривизны является
1 Кривизна плоской кривой из
.
dz 2
нейтрального слоя:
. курса дифференциальной
обратной величиной кривизны кривой:
k
EI x
3
k
dy 2
геометрии:
v=v(z)
В силу малости прогибов и углов, а следовательно, малости первой производной
ее квадратом по сравнению с единицей можно пренебречь:
d2y
k
Отсюда из формулы радиуса кривизны получаем:
2
2
M
d y
x .
2
dz
EI x
Выбираем знак плюс в соответствии с правилом знаков для изгибающих моментов
(Mx > 0, изгибает ось балки выпуклостью вниз)
d 2 y M x -дифференциальное
и второй производной функции прогибов
.
уравнение прогибов
( > 0, выпуклость кривой направлена вниз):
EI x
dz 2
1
dz
dz
Используя другие, полученные ранее,
дифференциальные зависимости можно получить:
d 3 y Qy
,
dz 3 EI x
d4y
q
.
4
EI x
dz
1
4. Лекция 1 (продолжение – 1.2)
Интегрирование дифференциального уравнения прогибов – выполняется обычными приемами решения дифференциальныхуравнений, рассматриваемых в курсе высшей математики: понижение степени производной, разделение переменной, интегрирование
левой и правой частей, определения констант интегрирования или подстановка переменных пределов. Рассмотрим процедуру на
примере двухопорной балки, нагруженной линейно изменяющейся распределенной нагрузкой.
Пример:
d2y Mx
1. Запишем дифференциальное уравнение прогибов:
.
y
q=q(z)=qBz/l
EI x
dz 2
qB
z
2. Составим выражение для изгибающего момента в произвольном сечении на расстоянии z:
z
2.1.
Отбросим интегрирования
опоры, заменим их
и найдем
величину условий:
реакций
Константы
C реакциями
и D находятся
из граничных
A
φ0
из
уравнений
равновесия:
B
q l
1
2
RA
v=v(z)
RB B .
M0;iA 0; R B l q B l l 0.
RB
1) z = 0, y(0) = 0;
D =y
=
0
2
3
3
l
3
q7B l q B l
q B l 2 0l 3; - Rl 5 l 1 q l 1 l 0.
1 M
C 0R A
.
.
y iB A 3 ClB 0.
2) z = l, y(l) = 0;
2.2. Вычислим изгибающийEI
EI6x 360
3
6 6l 20l 2
x
момент через левые силы:
q B l q l 21 3 z 25 q B l 2 7zq l z2 3
1 вид:1
Таким образом, уравнениеM
прогибов
имеет
1 z B qz B z
B .
R
z
q
(
z
)
z
z
x
A
l l 3 z.
2
3y EI6 6 6 6l l 3 6 360
20
l
x
EI x
3. Подставим
в дифференциальное
2
4
3
Или с использованием
1 q l z z
1 q B l d
уравнение
и понизимкоординат:
порядок производной:
. z .
y
( 7 10 3B 5 5 ), где
безразмерных
3
EI x 360 dz EI x 6 l l
l
4. ВРазделим
переменные
системе MathCAD
легко вычислить
от функции прогибов2 и
2
1 q B l 2 zпроизводные
z3
1 q B l zполучить
z4
и проинтегрируем:
последовательно используя дифференциальные
зависимости функцию
углов поворота,
d
3
dz.
C.
3
EI x и поперечной
6 l l силы, исходную распределенную
EI x 6 2l нагрузку,
4l а
эпюры изгибающих моментов
также положение максимальных значений прогиба (ξ =0,519) и изгибающего момента
Получили выражение для угла поворота сечения, в которое входит неизвестная
(ξ =0,577):
величина C (константа интегрирования), равная углу поворота φ0 в начале координат (в
Видно,
что величина максимального прогиба от такой нагрузки практически
точке
A z=0).
совпадает с прогибом, вычисленным в середине пролета, для 2изгибающего
dy
1 q B l z 2 z 4 момента
5. Представим
поворота
в виде
C.
разница чутьугол
больше
(2.57%).
производной от прогиба :
dz EI
6 2l 4l 3
x
6. Разделим переменные
и проинтегрируем:
1 qBl 2 z 2 z 4
C dz.
dy
3
EI x 6 2l 4l
y
1 qBl 2 z 3
z5
Cz D.
EI x 6 6l 20l 3
Получили выражение для прогиба, в которое входит неизвестные величины C и D
(константы интегрирования), где D равна прогибу y0 в начале координат (в точке A z=0).
2
5. Лекция 1 (продолжение – 1.3)
Интегрирование дифференциального уравнения прогибов при наличии нескольких участков – Балка, разбивается на участки вслучаях ступенчатого изменения сечения, присутствия сосредоточенных сил и/или моментов, а также в случае расположения начала
и/или конца распределенной нагрузки в пролете. Все это приводит к тому, уравнения изгибающих моментов, составляемые на каждом из
участков, справедливы только в пределах этих участков. На границах участков функции (эпюры) изгибающих моментов имеют резкие
переломы или скачки. Такие функции называются кусочно-гладкими и все операции дифференцирования или интегрирования
необходимо выполнять по каждому из участков по отдельности. После интегрирования на каждом из участков появляются по две
константы, подлежащие определению. Они определяются как и раньше из граничных условий. Для сечений, являющихся границами
смежных участков, такими условиями является равенства значений прогибов и углов поворота слева и справа от сечения (условия
совместности деформаций). Во многих случаях удобно использовать локальные координаты на каждом из участков.
Пример:
1. Отбросим связи, заменим их действие реакциями RA, RB и вычислим их:
Fb
F
Fa
y
M iA 0; Fa RB l 0; RB . M iB 0; Fb R A l 0; R A l .
z2
l
z1
2. Составим на каждом из участков выражения для изгибающих моментов, подставим
z в выражения упругой линии и дважды проинтегрируем их:
A
φ0
Fa
Fb
B
M 2 x R B (b z 2 )
(b z 2 ).
RA
M
R
z
z
.
v=v(z) a
1
x
A
1
1
b
l
l
RB
2
d y 2 d 2
Fa
d2y
d
Fb
l
Таким 1образом
(b z 2 ).
1 получили
z . уравнения линии прогибов:
1
dz 22 2 dz 23 EI x l
dz
EI x l
dz12
z 2 z 2 Fab(a b2 )
Fa
Fa 2 b 2
Fb z113 Fab
(
a
2
b
)
b
z2 z2
Fa
.
y1
z1 . y 2
Fb z12
1x
EI x l 2 2 6 bz32EI x l C 2 .3EI x l
EI
l 6
6 EICx1l.
EI x l
2
EI x l 2
3
2
Fb z1
Fa z 2 z 23
y1
C1 z1 D1 .
y2
b
C 2 z 2 D2 .
EI x l 6
EI x l 2
6
3. Для нахождения констант интегрирования имеем 4 граничных условия:
1). в сечении A: y1(0) =y10= 0;
2). в сечении B: y2(b) = 0;
3). на границе участков: y1(a) = y2(0);
4).
φ1(a) =φ2(0).
Fab 3
C 2 b D 2 0.
Из условия 1 сразу нашлось D1= 0. Из условия 2:
Из условий 3 и 4
имеем:
3
Fb a
C1a D2 .
EI x l 6
3EI x l
2
Fb a
C1 C 2 .
EI x l 2
Решить эту систему трех уравнений вручную не просто, но MathCAD легко справляется
с этой проблемой:
2
Fl 3
В частном случае при C Fl .
D
y
. 3
2
20
C 2 20 0.
1
10
48 EI x
16 EI x
a = b = l/2 получаем:
6. Лекция 2
Метод начальных параметров – Предыдущий пример показывает, что при двух участках приходится находить 4 константыинтегрирования. Соответственно, при m участков число констант интегрирования равен 2m. С помощью специального выбора
системы отсчета и использования некоторых приемов интегрирования можно добиться того, чтобы количество констант,
подлежащих определению, оставалось равным двум при любом числе участков:
Рассмотрим два соседних участка i и i+1, на границе между которыми приложен некоторый сосредоточенный силовой фактор,
например, сила F. Начало координат общее для всех участков и совпадает с левым концом балки.
i
i+1
Составим дифференциальные уравнения прогибов для этих двух участков (Mi, Mi+1 – изгибающие
моменты на участках i и i+1):
z
d 2 yi
d2y
EI x
F
zi
dz 2
M x ,i ( zi );
EI x
После интегрирования получим:
a
M x ,i 1 ( zi 1 ) M x ,i ( zi 1 ) F ( zi 1 a).
( zi 1 a) 2
EI x i 1 M x ,i ( zi 1 )dz F
Ci 1.
2
( z a)3
EI x yi 1 ( M x ,i ( zi 1 )dz )dz F i 1
Ci 1 zi 1 Di 1.
6
EI x i M x ,i ( zi )dz Ci ;
zi+1
dz
i 1
2
EI x yi ( M x ,i ( zi )dz )dz Ci zi Di ;
На границе участков zi = zi+1 = a углы поворота и прогибы должны быть одинаковы: φi = φi+1 , yi = yi+1 .
Тогда из равенства правых частей следует, что константы интегрирования равны для рассматриваемых смежных участков (слагаемые,
связанные с силой F, обращаются в ноль, а интегралы тождественно равны для каждого из участков):
Ci Ci 1 ; Di Di 1 .
Cоставляя подобные уравнения на каждой границе, получим, что на всех участках ( i =1,…,m) константы равны С1=...=Сi=…=Сm= EIxφ0, и
D1=...=Di=…=Dm= EIxy0, где φ0, y0 - угол поворота и прогиб в начале координат. Таким образом, при использовании указанной системы отсчета
при любом количестве участков получаем всего две константы, подлежащие определению, угол поворота и прогиб в начале координат,
называемые начальными параметрами.
Таким образом, получили следующие уравнения для угла поворота и прогиба для любого из участков:
qk
Mi
φ0
y0
Fj
ai
EI x ( z ) M x ( z )dz EI x 0 .
EI x y( z ) ( M x ( z )dz )dz EI x 0 z EI x y0 .
z
■
Выражение изгибающего момента, участвующее в уравнениях, составим в общем
виде для любого числа сосредоточенных моментов, сосредоточенных сил и равномерно
распределенных нагрузок, расположенных по одну (левую) сторону от рассматриваемого
сечения, согласно определения изгибающего момента, как сумму:
bj
ck
z
M x ( z) M i F j ( z b j ) q
i
j
k
( z ck ) 2
.
2
4
7. Лекция 2 (продолжение – 2.2)
Итак, в полученных интегральных уравненияхдля угла поворота и прогиба в произвольном сечении:
EI x y( z ) ( M x ( z )dz )dz EI x 0 z EI x y0 .
EI x ( z ) M x ( z )dz EI x 0 .
( z ck ) 2
M x ( z) M i F j ( z b j ) q
.
2
i
j
k
выражение для изгибающего момента имеет вид:
Первый интеграл представим
как сумму интегралов:
z
z
z
0
M x ( z )dz M i ( z ai ) dz F j ( z b j )dz q
i aj
j bj
(сомножитель (z – ai)0
добавили для “красоты”, нижние пределы задаются от координаты положения каждого силового фактора)
Проинтегрируем это выражение не раскрывая скобок
и подставим пределы:
2 z
z
M x ( z )dz M i ( z ai )
i
Fj
ai
(z b j )
2
j
bj
z
( z ck ) 3
q
.
6
k
c
M x ( z )dz M i ( z ai ) F j
i
k
Подстановка интеграла в выражение для угла поворота дает
следующее уравнение углов поворота:
i
( M x ( z)dz)dz M i
i
( z ai )
2
ai
Fj
j
(z b j )
6
3 z
q
bj
Подстановка интеграла в выражение для прогиба дает
следующее уравнение прогибов:
k
( z ck )
24
4 z
(z b j )2
2
j
2
q
k
( z ck ) 3
q
.
6
k
( z ck ) 3
EI x 0 .
6
(z b j )
( z ai ) 2
( z ck ) 4
(
M
(
z
)
dz
)
dz
M
F
q
.
i i 2
j j 6
k
x
24
3
.
ck
EI x y ( z ) M i
(z a j )2
2
i
(z b j )2
j
EI x ( z ) M i ( z ai ) F j
Вычислим второй интеграл подобным образом:
2 z
k ck
( z ck ) 2
dz.
2
Fj
( z b j )3
6
j
q
k
( z c k )4
EI x 0 z EI x y 0 .
24
Таким образом получено у н и в е р с а л ь н о е уравнение упругой линии (прогибов) балки, называемое также, как
уравнение метода начальных параметров:
2
3
(запись слагаемых в порядке увеличения степени координаты
и использование факториалов придает особенную изысканность
и красоту или, лучше сказать, простоту)
Уравнение для углов поворота может быть теперь
получено дифференцированием уравнения
метода начальных параметров:
EI x y ( z ) EI x y 0 EI x 0 z M i
(z a j )
2!
i
EI x ( z ) EI x 0 M i ( z ai ) F j
i
j
Fj
(z b j )
3!
j
(z b j )2
2!
q
k
q
k
( z c k )4
.
4!
( z ck ) 3
.
3!
Иногда в литературе [1] в число начальных параметров включается изгибающий момент M0, поперечная сила Q0 и даже q0 , как силовые
факторы, имеющиеся (приложенные) в начале координат (в силу особенности вывода). Они вполне могут быть причислены к обычным
силовым факторам, приложенным по длине балки, т.е. включены в соответствующие суммы, полагая a0 = 0, b0 = 0, с0 = 0.
5
8. Лекция 2 (продолжение – 2.3)
Напомним правила, используемые при выводе (или составлении) уравнения начальных параметров:1. Начало координат для всех участков общее и совпадает с началом балки.
2. В выражение изгибающих моментов (или в число слагаемых уравнения начальных параметров) включаются только те силовые факторы, что
находятся левее рассматриваемого сечения.
3. Интегрирование производится не раскрывая скобок.
4. Равномерно распределенная нагрузка раз начавшись не должна заканчиваться. Если она закончилась левее сечения, то можно считать, что
она продолжается, но необходимо добавить такую же нагрузку противоположного направления, начинающуюся там, где кончалась заданная
нагрузка.
5. Правило знаков для слагаемых от любого фактора соответствует правилу знаков изгибающего момента для этого фактора.
Пример. Определить прогибы в середине пролета и на конце консоли двух опорной балки от приложенной равномерно распределенной нагрузки
в пролете.
1. Отбросим опоры и заменим их действие реакциями:
y z1
ql
.
2. Составим уравнения равновесия и определим реакции: R A R B
q z2
yD
2
3. Составим уравнения начальных параметров на первом и втором участках (на втором
D z
A
участке продлим нагрузку q и добавим противоположную по направлению) :
C yC
B
z3
z4
RA
RB
EI x y ( z1 ) EI x y0 EI x 0 z1 RA 1 q 1 , (0 z1 l );
3!
4!
3
z
( z l )3
z4
( z l )4
EI x y ( z2 ) EI x y0 EI x 0 z2 RA 2 RB 2
q 2 q 2
, (l z1 l a).
3!
3!
4!
4!
EI x y A EI x y z 0 EI x y0 0;
3. Определим начальные параметры из граничных условий: y =0, y = 0. Из первого условия:
l
a
A
B
1
l2
l3
ql l 2
l3
ql 3
l3
l4
EI x 0 RA q
q
;
q 0;
1
3!
4!
2 6
24
24
3!
4!
3
4
ql 3 l ql 1 l
1 l
5ql 4
EI
y
EI
y
(
)
q
l
4. Определим прогиб в середине пролета:
x C
x
z1
24 2 2 3! 2
4! 2
384
2
Прогиб на конце
ql 3
ql 1
ql
1
1
1
qal 3
3
3
4
4
EI
y
EI
y
(
)(
l
a
)
l
a
a
q
l
a
q
a
консоли:
x D
x
z 2 l a
24
2 3!
2 3!
4!
4!
24
Из второго условия:
EI x y B EI x y z l EI x 0l RA
Этот же результат можно получить используя
угол поворота на опоре B с учетом симметрии:
ql 3
qal 3
EI x y D EI x B a ( EI x 0 )a ( )a
24
24
В системе MathCAD эта задача решается достаточно просто с использованием
условных операторов if(…), обеспечивающих выполнение правила 2:
6
9. Лекция 3
Принцип возможных перемещений – Для равновесия механической системы, подчиненной голономным (интегрируемым),стационарным, идеальным и двухсторонним связям, необходимо и достаточно, чтобы
сумма элементарных работ всех приложенных активных сил на любом
A F 0.
возможном перемещении из предполагаемого положения равновесия равнялось нулю:
Напомним, что под возможными перемещениями понимаются любые бесконечно малые перемещения системы, допускаемые связями.
Таким образом, возможные перемещения твердого тела в теоретической механике, а здесь, в механике деформируемого тела, перемещения,
связанные, как правило, с деформациями, не зависят от величины и направления активных сил, например, нагрузки.
С использованием принципа возможных перемещений может быть получена формула для определения действительных перемещений
по некоторому заданному направлению от приложенной к системе нагрузки. Такое направление можно задать с помощью приложения условного
единичного силового фактора. Таким образом, можно рассматривать два состояния системы: “грузовое” (“q”) – от действия заданной нагрузки
и “единичное” (“1”) – от действия единичного силового фактора, приложенного по направлению искомого перемещения:
Рассмотрим состояние “1”: Под действием силы F1 в каждом из поперечных сечений возникают
внутренние упругие (реактивные) усилия – изгибающий момент M x1 и поперечная сила Q y1 ,
y
y1q
q
сопротивляющиеся деформации балки и совершающие работу на любом возможном перемещении
q
из положения равновесия, т.е. не являющиеся идеальными.
Q yq
z
Их можно причислить к активным (заданным) силам.
A
d q
В
качестве возможных перемещений можно взять действительные перемещения от нагрузки
D
B
(состояние “q”), т.к. они достаточно малы и подчиняются наложенным на систему идеальным связям
M
M xq
(перемещения опорных точек равны нулю). и составить сумму работ заданных сил на возможных
a
l xq
Q yq
перемещениях:
AF AR 0.
Возможная работа единичной силы равна A 1 y1q 1 y1q , где y1q – искомое перемещение
(здесь и далее знак вариации перемещений опускается, поскольку возможные перемещения и
действительные перемещения отождествляются).
Возможная работа внутренних сил, приложенных к системе от деформации каждого упругого элемента
балки, равна произведению внутреннего усилия на соответствующее перемещение. Поскольку
во многих случаях при изгибе влиянием поперечных сил на деформацию пренебрегается, то,
ограничиваясь изгибающим моментом, возможная работа внутренних усилий, действующая
на систему от каждого элемента
M xq ds
M xq ds
dA R M x1
.
.
dA R M x1 d q , где d q
F
y
M x1
Qy1
1
y11
A
B
Q y1 M x1l
z
D
a
F1 1
EI x
EI
x
Для вычисления возможной работы внутренних при деформации всех элементов балки
sk M M ds
необходимо проинтегрировать по участкам, на которых эпюры изгибающие моменты
Работа внутренних (реактивных)
x1 xq
A R
. сил всегда противоположна по знаку
не имеют переломов и скачков, и просуммировать по количеству участков:
EI
Подставляя возможные работы от единичной силы
sk M M ds
и внутренних усилий в сумму работ (принцип
x1 xq
0
1 y1q
возможных перемещений), получаем:
k 0
EI x
k 0
sk M
y1q
k 0
x1 M xq ds
EI x
x
работе внешних (активных) сил)
на любых возможных перемещениях.
- формула Максвелла-Мора
4
10. Лекция 3 (продолжение – 3.2)
В общем случае для вычисления перемещений по некоторому произвольному направлениюn с учетом деформаций сдвига и сжатия формула Максвелла-Мора принимает вид:
sk M
nq
xn M xq ds
EI x
k 0
si Q
i 0
yn kQyq ds
GA
sj
N n N q ds
j 0
EA
.
Здесь использованы соответствующие соотношения для вычисления возможной работы внутренних сил:
dA R M xn d q Q yn q ds N n dsq
и деформаций:
d q
M xq ds
, q
kQyq
ds q
N q ds
, где k – коэффициент, учитывающий
неравномерность распределения
касательных напряжений при изгибе
Итак, из принципа возможных перемещений получена формула Максвелла-Мора (или просто формула Мора), позволяющая определить
действительные перемещения в любой точке упругой системы по любому направлению. Для этого необходимо:
1. Выбрать “единичное” нагружение, соответствующее искомому перемещению, а именно:
при вычислении линейного перемещения в какой-либо точке система нагружается единичной сосредоточенной силой
в этой же точке и по тому же направлению (с точностью наоборот), в котором ищется перемещение;
при вычислении углового перемещения (угла поворота) какого-либо сечения система нагружается единичным
сосредоточенным моментом (парой сил) в этом же сечении.
2. Построить эпюры внутренних сил от нагрузки (грузовое состояние) и от единичного силового воздействия. При плоском изгибе, как правило,
ограничиваются построением эпюр изгибающих моментов. В некоторых случаях, например, в случаях сложного сопротивления, строятся
дополнительно другие эпюры. Например, при сжатии с изгибом необходимо построение также эпюр продольной силы.
3. Применить формулу Мора. Если результат оказывается больше нуля, то это значит, что найденное перемещение совпадает с заданным
направлением единичного силового воздействия. Если меньше нуля, то найденное перемещение противоположно направлению единичного
воздействия.
Пример. Определить прогиб и угол поворота сечения на конце консоли двух опорной балки от приложенной равномерно распределенной нагрузки
в пролете.
1.
К грузовому состоянию добавляем два единичных состояния: “1” – от действия единичной силы,
y
D
q
q
A
B
l
GA
EA
,
приложенной в точке D вертикально, например, вниз; “2” – от действия единичного момента, приложенного
в этой же точке, например, против часовой стрелке:
2.
Строим эпюры изгибающих
yD
M2=1
F1=1
моментов
во всех трех состояниях:
1
2
D z
z
D z
A
A
3.
Применить формулы Мора
B
B
D
для прогиба и угла поворота:
a
a
l
Mq
ql 2
8
EI x
,
a
l
a
M2
M1
1
1
2 sk
yD
M 1M q ds
k 1 0
EI x
2 sk
M 2 M q ds
k 1 0
EI x
D
5
11. Лекция 4
Способы вычисления интеграла Мора – Интеграл Мора, в котором подинтегральное выражение есть произведение двухфункций, может быть вычислен различными методами в зависимости от вида этих функций. Заметим, одна из них, связанная с
эпюрой внутренних усилий от единичного сосредоточенного воздействия, всегда линейная.
1. Непосредственное интегрирование – практически не имеет ограничений по использованию.
2. Способ Верещагина – удобен на тех участках, на которых легко можно определить центр тяжести одной из эпюр (обычно это
относится к эпюре от грузового воздействия).
3. Формула Симпсона – применима в случае квадратичного закона изменения эпюры от грузового воздействия Формула трапеций
– применяется в случае линейности обоих эпюр.
4. Формула трапеций – применяется в случае линейности обоих эпюр.
Первый способ не требует никаких особых пояснений. Рассмотрим его на примере (см. лекцию 3):
D
y
q
q
yD
1
Mq
ql
8
l
yD
0
M 1M q dz
EI x
2
a
l
a
M q ( z)
B
B
B
l
D
0
M 2 M q dz
EI x
M 1M q ds
k 1 0
EI x
M q ( z)
a
z.
l
2 sk
M 2 M q ds
EI x Мора может
Таким образом,k 1интеграл
0
быть вычислен, как произведение
Грузовая эпюра на втором участке
площади криволинейной эпюры на
тождественно равна нулю, так
ординату линейной эпюры, взятой
что достаточно знать законы
под центром тяжести криволинейной
M
2 изменения изгибающих моментов
эпюры (способ Верещагина).
лишь на первом участке.
a
a
ql
qz 2
z
.
2
2
M1
1
M q ( z ) z.
l
1
1
l
l
l
1 z ql
qz 2
1 qz 3 qz 4
1 ql 3
z
zdz
0.
EI x 0 l 2
2
EI x 2 3 2 4l 0 EI x 24
l
M M dz
Способ Верещагина:
l
1 a ql
qz 2
1 qaz 3 qaz 4
1 qal 3
z
zdz
0.
EI x 0 l 2
2
EI x 2 3 2 4l 0
EI x 24
z
D
D
l
Здесь отрицательное значение прогиба означает, что действительное
направление перемещения противоположно заданному направлению
единичной силы.
l
M2=1
2
F1=1
D zA
D z A
A
2 sk
yD
1
q
Вычисление интеграла вида 0
может быть представлено
как “перемножение” эпюр, если одна из эпюр линейная, что мы и
имеем для эпюр изгибающих моментов от действия сосредоточенных
усилий.
M ( x a)tg .
1
l
C
y’
Mq
l
l
M1M q dz (a z)tg M q dz tg (a z)d Mq .
0l
0
q
(a z)d M q (a zC ) M q S y' .
0
M
dz
Здесь положительное значение угла поворота означает, что действительное
направление угла поворота совпадает с заданным направлением единичного
момента.
l
zC
z
-статический момент площади
эпюры Mq относительно оси y’
M1
yC
a
0
l
M M dz tg (a z ) .
1
q
C
0
yC
Mq
6
12. Лекция 4 (продолжение – 4.2)
Справочные данные о площадях и положениях центров тяжести характерныхэпюр:
2hl
hl
hl
h
3
3
2
l
4
l
3
3l
8
l
Следует иметь в виду, что приведенные формулы для
площади и координаты центра тяжести не справедливы для
“не чистой” квадратной параболы, являющейся результатом
сложения линейной эпюры (от действия сосредоточенных
сил на границе участка) и параболической (от действия
равномерно распределенной нагрузки на участке).
Если это так, то следует разбить эту эпюру на две или три
более простых эпюры:
q
l
h
Пример. Вычислим прогиб и угол поворота сечения на конце консоли для предыдущего примера
способом Верещагина:
Mq
l
ql 2
8
l
yD
0
M1M q dz
EI x
1 2 ql 2 a
1 qal 3
l
.
EI x 3 8 2
EI x 24
l
D
0
M 2 M q dz
EI x
ql 2
8
l
1 2 ql 2 1 1 ql 3
l
.
EI x 3 8 2 EI x 24
Формула Симпсона: Можно доказать, что разбиением сложной параболической эпюры, как было показано
выше, результат “перемножения” такой эпюры с линейной эпюрой выражается формулой:
a
l
a
e
b
M1
l
l
M2
c
1
f
1
l
0 M1M q dz 6 (ac 4ef bd )
d
yD
M1M q dz
l
M 2 M q dz
0
D
0
a
b
EI x
1 l
ql 2 a
1 qal 3
0 0 4 0 a
.
EI x 6
8 2
EI x 24
1 ql 3
1 l
ql 2 1
0 0 4
0 a
.
EI x 6
8 2
EI x 24
Формула трапеций: Формула Симпсона в частном случае при
линейности обеих эпюр (перемножение трапеций)
выражается формулой:
l
l
c
EI x
Воспользуемся формулой Симпсона
для предыдущего примера:
l
M 1M q dz 6 (2ac ad bc 2bd )
0
d
7
13. Лекция 5
■ Основы расчета статически неопределимых систем методом сил – Напомним, что статически неопределимыми системаминазываются такие системы, в которых число неизвестных усилий (опорных реакций) превышает число независимых уравнений равновесия,
которые можно составить для рассматриваемой системы. Это означает, что статически неопределимая система имеет дополнительные связи,
которые с точки зрения обеспечения неизменяемости системы, рассматриваемой как совокупность абсолютно твердых (недеформируемых) тел,
являются лишними.
■ Количество таких “лишних” связей (разность числа искомых неизвестных усилий и числа независимых уравнений равновесия) характеризует
степень статической неопределимости системы. Степень статической неопределимости плоской системы может быть установлена рассмотрением
степени кинематической подвижности: W = 3Д – С – 2Ш – 3Ж, где Д – число дисков (твердых дел), С – число стержней, Ш – число шарниров,
Ж – число жестких заделок. При W = 0 система статически определима, при W < 0 – статически неопределима, при W > 0 – геометрически изменяема.
■ Иногда при достаточном числе связей они стоят так, что они не могут препятствовать определенным перемещениям. Такие системы
являются геометрически изменяемыми, как и системы с недостаточным числом связей. В некоторых случаях связи не включаются в работу
при малых перемещениях (деформациях) системы. Такие системы являются мгновенно изменяемыми системами. Для них характерно возникновение
значительных (близких к бесконечности) усилий в связях в положениях, в которых возможно равновесие .
Примеры:
F
A
D zA
B
l
D zA
B
a
F
F
F
D z
A
l
D z
B
B
a
l
a
l
a
Статически определимая балка
Геометрически изменяемая система
Статически неопределимая балка
Мгновенно изменяемая система
(W = 3∙1 – 1 – 2∙1 = 0)
(W = 0, система не может
(W = – 1, прогибы значительно
В уравнения совместности деформаций войдут перемещения от нагрузки и лишних неизвестных. (не может воспринимать
воспринимать горизонтальную
меньше)
Перемещения от каждого силового фактора связаны с усилиями упругими соотношениями,
горизонтальную нагрузку
нагрузку)
например, формулами Мора. Таким образом, как и ранее, образуется полная система уравнений, при малых перемещениях)
Таким образом,
последниетри
двестороны
системы
не могутстатически
нести нагрузку,
методы выявления
таких систем
отражающая
описания
неопределимой
задачи (статика
– уравнения
изучаются в равновесия,
курсе строительной
механики.
Статически
неопределимые
системы
обладают
повышенной жесткостью и несущей
геометрия – уравнения деформаций, физика – соотношения упругости).
способностью. Поэтому они широко используются в строительной практике.
■ Расчет статически неопределимых систем методом сил основывается на использовании основной статически определимой системы,
образованной из исходной статически неопределимой системой отбрасыванием лишних связей. Действие отброшенных связей заменяется силами,
называемыми лишними неизвестными. Таким образом в уравнения равновесия системы войдут эти дополнительные неизвестные усилия.
Для нахождения лишних неизвестных составляются уравнения совместности деформаций ( или просто уравнений деформаций), смысл которых
заключается в том, перемещения в основной системе от действия нагрузки и лишних неизвестных усилий по направлению каждой из лишних
неизвестных должны отсутствовать (обращаться в ноль):
1 0; ... i 0; ... n 0, где n – количество лишних неизвестных.
8
14. Лекция 5 (продолжение – 5.2)
■ Система канонических уравнений метода сил – Уравнения деформаций могут быть записаны более подробно с выделением слагаемых отдействия неизвестных сил и нагрузки:
Слагаемые от действия неизвестных
1 1 ( X 1 ) ... 1 ( X i ) ... 1 ( X n ) 1q 0, удобно представить в виде произведения
1 0; ... i 0; ... n 0.
......................................................................... перемещения от единичного усилия
на величину этого усилия:
i i ( X 1 ) ... i ( X i ) ... i ( X n ) iq 0,
.........................................................................
n n ( X 1 ) ... n ( X i ) ... n ( X n ) nq 0.
Подставляя эти соотношения
в уравнения деформаций получим
систему канонических уравнений
метода сил:
11 X 1 ... 1 j X j ... 1n X n 1q 0,
............................................................
i1 X 1 ... ij X j ... in X n iq 0,
...........................................................
n1 X 1 ... nj X j ... nn X n nq 0.
В случае учета деформаций сжатия-растяжения, например, при наличии в
системе стержней, работающих только на сжатие-растяжение, формулы для
перемещений содержат соответствующие дополнительные слагаемые:
i ( X j ) ij X j ; (i, j 1,..., n)
Здесь бij – перемещение по направлению
i –ого неизвестного от действия единичной силы
по направлению j – ого неизвестного:
Перемещения бij и iq при изгибе определяются
формулами Мора:
sk M M ds
ij
k 0
sk
ij
k
0
M i M j ds
EI
sk
k
0
Ni N j ds
EA
Решением системы канонических уравнений
Пример 1.
находятся неизвестные X1,…Xn, после чего
1. Выбираем основную систему (отбрасываем среднюю
Проверим правильность расчета вычислением перемещения
могут
бытьопоры
найдены
внутренние усилия,
также
опору и заменяем ее действие неизвестным усилием X1. A
средней
(деформационная
проверка):
как это делается в статически определимых
2. Строим эпюру изгибающих моментов от нагрузки
1 1 l l 2 Fa
системах. 2 l / 2 M 1 Mds
в основной системе:
1q
Посколькуkэпюры
внутренних
EI
EI усилий
2 4 2от
3. Строим эпюру изгибающих моментов в основной
1 0
3 4
единичных воздействий и нагрузки, построенные системе от действия единичного усилия X = 1.
1
l перемещений,
l Fa l уже имеются,
Fa то
для определения
4. Запишем
2
Fa
0 2 Fa
0 0. каноническое уравнение метода сил и
расчетные
2 6 EIэпюры
4 4 быть
4
4
построены
вычислим
коэффициенты:
могут
11 X 1 1q 0.
непосредственно суммированием воздействий
l/2
от найденных неизвестных усилий и нагрузки.
M M ds
2 1 l l 2 l
l3
11 2 1 1
,
Например, для расчетной эпюры
EI
EI 2 4 2 3 4 48 EI
0
изгибающих моментов:
2 l / 2 M M ds
1 1 l l 2 Fa 1 1 l l 4 Fa Fl 2 a
1
q
M M1 X1 ... M i X i ... M
1nqX n M q .
.
EI
EI 2 4 2 3 2 EI 2 4 2 3 2 16 EI
k 1 0
1q
3Fa
5. Вычислим величину X1 : X 1
. 6. Построим эпюру M1X1 и сложим ее с эпюрой Mq:
11
l
i
sk
iq
j
EI
k
sk
iq
k
0
M i M q ds
EI
M i M q ds
EI
0
sk
k
0
l
2
X1
Ni N q ds
EA
F
D z
B
a
l
Fa
Fa
2
Mq
l
4
+
Fa
4
M1
Fa
3Fa
4l
M1X1
M
9
15. Лекция 5 (продолжение – 5.3)
q■ Пример 2 – Построить эпюры изгибающих моментов, поперечных и нормальных сил в раме путепровода
(высота стойки равна половине пролета H = l/2):
1. Определяем степень статической неопределимости n = -W = -(3Д – С – 2Ш – 3Ж) = -(3∙1 - 2 - 2∙0 - 3∙1) = 2.
2. Выбираем основную систему (отбрасываем левую и правую опоры и заменяем их действие неизвестными
усилиями X1 и X2:
3. Строим эпюру изгибающих моментов от нагрузки:
4. Строим эпюры изгибающих моментов от действия: единичных усилий X1 = 1и X2 =1:
11 X 1 12 X 2 1q 0,
5. Запишем систему канонических уравнений метода сил
и вычислим коэффициенты:
2 sk M M ds
1 1
11
k 1 0
EI k
1
80в матричном виде,
используя MathCAD:
ql
80
7. Построим эпюры M1X1 и M2X2
и сложим их с эпюрой Mq:
3 2
33 2
M80 qlM1 X1 M 2 X 2 M80q .ql
4
k 1 0
EI k
2 sk M
2 M q ds
k 1 0
EI k
2q
X2
X1
ql 2
2
7 X 2
12
1
8
Mq
EI
H=l/2
2EI
l
EI
M1
l
l
X1=1
2EI H=l/2
l
M2
l
l
X1=1
2EI
X1
M1X1
8. Выполним
деформационную
проверку: M2X2
1q
l
l
в систему канонических уравнений и ее
M 1 M 2 ds
1 l
l3
решения находим:
l
l
можно
21. построить эпюры
33
лишние
12
Поскольку
неизвестные определены,
X1
ql 0.425ql ;
2
EI
2
EI
2
4
EI
0
поперечных и нормальных сил обычным образом (методом сечений):
80
2 sk M M ds
1 1 ql 2 3
1 ql 2 l
ql 4
1
q
3
l
1q 33 ql
3
l l
.
2 2
X 2 ql 0.0375ql.
ql 3 2
80k 1 0
EI k
EI
4
2
EI
4
EI
80
80
2
4
l /+
2 M M ds
1
ql
l
ql
7
1
Систему
уравнений
2
q
1
l
2q
.
X
50
удобно
решить
2 2
12
4 1 4 ql
247EI
2 EI
8 EI N
Q
ql
0
H
2EI
21 X 1 22 X 2 2q 0.
1 1 2
1 l
7 l3
22 .
l l l
l l
6. После подстановки полученных выражений
EI 2 3
2 EI 2 12 EI
l/2
2 sk M M ds
1
q
EI
EI
l
X1
2
2
7 ql
80
7ql
l
l 13ql
1 l 4ql
0.
0 0 4
l
l
6 EI
2 160
80 2 EI 2 80
2
2
1 1 2 2 3ql
1 l 4ql
0.
l
l
EI 2 3 80 2 EI 2 80
2
3ql 2
80
M
EI
2
13ql 2
160
2EI
4 ql 2
80
10
16. Лекция 6
Сложное сопротивление – Рассмотренные ранее случаи сопротивления прямого стержня, когда в сечении возникает лишь один видвнутреннего усилия, относятся к простым деформациям стержня: осевое растяжение-сжатие, чистый сдвиг, чистый (плоский) изгиб,
чистое кручение. В реальных конструкциях стержни могут подвергаться более сложным видам сопротивления, представляющих собой
сочетание нескольких простых деформаций, происходящих одновременно. Таким образом, возможно появление в поперечном сечении
различных комбинаций ненулевых компонент из шести внутренних усилий: N, Qx, Qy, Mx, My, Mz. Такие комбинации, например, возникают
в поперечных сечениях пространственного ломаного стержня (рычаги сложной конфигурации, коленчатые валы и т.п.) даже при нагрузке,
лежащей в одной плоскости.
■ Построение эпюр внутренних сил в пространственном ломаном стержне – Для определения
y
x
опасных сечений в таком стержне необходимо построить эпюры компонент внутренних усилий: N, Qx, Qy,
y
Mx, My, Mz. При построении эпюр следует руководствоваться следующими правилами:
z
1. Как и ранее, стержень разбивается на участки, границами которых являются сечения, в которых
I
II
x
приложены сосредоточенные усилия (сила, момент-пара сил), начинается или заканчивается равномерно
y
распределенная нагрузка (в том числе и распределенный крутящий момент). Границами участка являются
x
z
также начало и конец ломаного стержня. Теперь дополнительно границей участка следует считать
z
перелом оси стержня.
III
IV
2. Вместо глобальной системы координат, с учетом пространственного изменения положения оси стержня
V
x при переходе от участка к участку, удобно использовать локальные системы координат для каждого
из прямолинейных участков с началом, совпадающим с центром тяжести рассматриваемого поперечного
y
сечения. Ось z направляется по оси прямолинейного участка бруса, положительные направления осей
z
x и y, в общем могут выбираться произвольно, но рекомендуется для горизонтальных участков ось y
направлять вверх, ось x – вправо от оси y при взгляде навстречу оси z (правая система координат). Для других
y
(вертикальных, наклонных) участков положительное направление оси y можно выбирать произвольно,
F1
F3 ось x – по тому же правилу.
My
3. Правило знаков для внутренних усилий. Напомним, что внутренние усилия определяются методом
сечений, в результате которого в поперечном сечении появляются напряжения, заменяющие действие
R
Q
RR
yz
Mz
Nx
отброшенной части бруса, которые и приводятся в общем случае к шести компонентам внутренних усилий
z
O
Ryx
Q
F4 N, Qx, Qy, Mx, My, Mz.
M0
Mx
Поскольку внутренние усилия, приложенные к каждой из частей бруса (оставленной или отброшенной) имеют
противоположные друг к другу направления (аксиома действия и противодействия), то при определении знака
F2
x
каждого из усилий используются не знаки проекций на оси, которые будут различны для каждой из частей, а
характер деформаций, которые остаются одинаковыми для обоих частей. Поэтому принимается:
продольная сила N - положительна, если приложенная к сечению сила растягивает рассматриваемую часть;
изгибающие моменты Mx, My – положительные, если приложенные к сечению силы растягивают нижние волокна бруса;
крутящий момент Mz - положителен, если при взгляде навстречу внешней нормали к сечению поворачивает его по часовой стрелке;
поперечные силы Qx, Qy - положительны, если при взгляде навстречу к заданной другой (парной) координатной оси, перпендикулярной оси
стержня, поворачивают сечение по часовой стрелке:
11
Теперь на рисунке слева все внутренние усилия показаны положительными.
■
17. Лекция 6 (продолжение – 6.2)
■ Построение эпюр внутренних сил – Выполняется методом сечений так же, как и ранее:1. Отбрасываются связи, заменяется их действие реакциями:
Для статически определимого пространственного стержня число связей (и реакций) равно 6. В данном примере жесткая пространственная заделка
должна быть заменена 3 реактивными силами RAx,RAy,RAz и 3 реактивными опорными моментами MAx, MAy, MAz :
X i 0; M xi 0;
z1
2. Определяются реакции из 6 уравнений равновесия:
y a =1
x
Yi 0;
M уi 0;
Замечание: В данном примере реакции можно не вычислять,
MAy
поскольку
далее
при
определении
внутренних
усилий
можно
рассматривать
RAy My
Z i 0;
M zi 0.
силы, приложенные к правой отсеченной части.
z
Mz
y
Qx
MAx A RAx
3. Определяется число участков, на которых не изменяется нагружение и геометрия – 5 и назначается
c = 1.8
N
ориентация локальных систем координат на каждом из прямолинейных частях бруса - 4:
I
II
x d = 0.8
Qy
4. Проводим сечение I-I на расстоянии z1 от начала участка (0 < z1 < a), отбрасываем левую часть и
y
q
RAz M M
заменяем ее действие внутренними усилиями+(все усилия показываем положительными):
x
Az x
z
d
5. Составляем уравнения
M xi 0; M x (qd )(c z1 ) Fe 0;
X i 0; Qx 0;
z IV
III
равновесия
2
M=qa2 y
M yi 0; - M y M Fb 0;
b=1
для оставленной
Yi 0; - Q y qd 0;
V
x
z1
правой части бруса:
M zi 0; M z (qd )b 0.
Z i 0; - N F 0;
y
a
e = 0.9
F=qe
x
d
z
отброш.части
Из уравнения равновесия Qx 0;
M x (qd )(c z1 ) Fe;
y
Qx X i
;
z
My
2
x
находим выражения
Qy
Q
qd
;
M
M
Fb
;
отброш.части
y
y
для внутренних сил:
Qy Yi
;
N
z
M z (qd )b.
N
F
;
отброш.части
d
Легко можно убедиться, что внутренние усилия равны алгебраическим суммам N
Zi
.
Mz
Qx
Mx b
q
проекций на оси и моментам сил правой части, приложенных к поперечному
отброш.части
сечению левой части. Таким образом, при вычислении внутренних сил можно
M x M xi
;
отбросить правую часть, оставить левую, а силы правой части перенести в
M
c
отброш.части
поперечное сечение левой. Естественно, что при переносе силы параллельно
M y M уi
;
e
самой
себе
возникает
пара
сил,
момент
которой
равен
моменту
этой
силы
1.93q
2.73q
M
Q
отброш.части
Nzyx
M z M zi
.
относительно новой оси (метод Пуансо):
-F=qe
0.1q
M
0.8q
0.1q
0.9q
0.8q
x 0.9q
6. Строим эпюры внутренних сил на рассматриваемом участке:
0.8q
0.8q
Qx = 0;
Mx = -(qd)(c-d/2+(a-z1))-Fe = -q0.8 (1.8 - 0.4+1-z1)- 0.9q∙0.9= -2.73q + 0.8qz1; z1=0, Mx= -2.73q;
z1=1, Mx= -1.93q;
Qy = -qd = -0.8q ;
My = M-Fb = q∙12- 0.9q∙1= 0.1q;
N = -F=-qe = -0.9q ;
Mz = -(qd)b = - q∙0.8∙1= -0.8q;
Далее строим эпюры внутренних сил на следующих участках, непосредственно используя
соответствующую систему локальных координат и данное выше определение внутренних сил:
12
18. Лекция 6 (продолжение – 6.3)
7. Проводим сечение II-II на расстоянии z2 от начала участка (0 < z2 < b) :Mx = -(qd)(b-z2) = -0.8q∙1+0.8qz2; z2=0, Mx= -0.8q; z2=1, Mx= 0;
Qx = F = 0.9q ;
a =1
y
z2
x
y
A
z
II
y
z
III
z3
M=qa2
c = 1.8
x
d = 0.8
y
x
z
b=1
N=0;
Mz = (qd)(c-d/2)+Fe = q∙0.8(1.8-0.4)+(0.9q)0.9= 1.93q;
y
z
IV
z4
V
z5
y
F=qe
z2=0, My =0.1q;
z
y
Mz = 0;
N = -F=-qe=- 0.9q;
Qy
-
N
0.8q
-
0.9q
0.8q
0.9q
0
0.8q
0.8q
-
0.9q
0.9q
0.9q
-
Mx
My
+
-
0.1q
+
1.13q
1.93q
1.93q
1.93q
0.8q
1.05q
0.1q
0.81q
q
-
0.81q
0.8q
-
0.9q
N = 0;
Mx = 0;
My = -F(e-z5)=-qe(e-z5)=
-q0.9(0.9-z5);
z5=0; My = -0.81q;
z5=0.9; My = 0;
Mz = 0;
Mz
0.1q
0.
z3=0, Mx= -1.13q;
z3=0.4, Mx= -1.05q;
z3=0.8, Mx= -0.81q;
10. Проводим сечение V-V
на расстоянии z5 от начала
участка (0 < z5 < e) :
Qx = -F=-qe=-0.9q;
Qy= 0;
0.9q
-
0.9q
2.73q
z2=1, My =q;
N = -F=-qe=- 0.9q; Mz = 0;
9. Проводим сечение IV-IV на расстоянии z4 от начала участка (0 < z4 < d) :
x
Qx = 0;
Mx = -q(d-z4)(d-(d-z4)/2)-Fe = -q∙(0.8-z4)(0.8-(0.8-z4)/2)-0.9g0.9;
e = 0.9 Qy =-q(d-z4) =-0.8q+qz4; z4=0, Qy=-0.8q; z4=0.8, Qy=0;
My =0;
0.9q
Qx
My = M-F(b-z2)= q∙12- 0.9q(1-z2);
8. Проводим сечение III-III на расстоянии z3 от начала участка (0 < z3 < (c-d)) :
Mx = -(qd)(c-d/2-z3)-Fe = -0.8q∙(1.8-0.4)-0.9g0.9+0.8qz3; z3=0, Mx= -1.93q;
Qx = 0;
z3=1, Mx= -1.13q;
Q = -qd = -0.8q ;
M =0;
q
x
Qy = -qd = -0.8q ;
+
0.8q
1.93q
Правильность построения
эпюр внутренних усилий
можно проверить
рассмотрением равновесия
вырезанных узлов (мест
сопряжений прямолинейных
участков).
13
19. Лекция 7
■Одновременное действие продольной силы и изгибающих моментов – Такая комбинация внутренних усилий характерна тем, что в
поперечном сечении возникают нормальные напряжения, которые могут вычисляться по отдельности и складываться в соответствии с
принципом независимости действия сил:
My
Здесь x, y – координаты точки, в которой отыскивается напряжение;
N Mx
y
x
.
M
z
M
правила знаков изгибающих моментов соответствуют ранее принятым
y
N
x
A Ix
Iy
x
y
y
правилам для плоского изгиба.
Iy
I
A
x
Во многих учебниках, например [1], можно увидеть знаки + перед слагаемыми, которые
записываются ценою изменения направления осей x, у на противоположные или изменения
My
правил для знаков изгибающих моментов (моменты считаются положительными, если они
y
вызывают растяжение волокон, находящихся в первом квадранте, т.е. при x > 0 и y > 0).
z
Иногда формулу напряжений при совместном действии продольной силы и моментов
+
+
+
+
N
записывают в виде:
Здесь x, y – расстояния точки от координатных осей, в которой
My
N Mx
z
y
x. отыскивается напряжение; изгибающие моменты берутся по модулю;
+
знаки слагаемых присваиваются по характеру деформаций
A Ix
Iy
(растяжение или сжатие) от каждого из моментов.
Далее, сохраняя обычную ориентацию координатных осей, будем использовать новое правило для знаков изгибающих моментов
(моменты считаются положительными, если они вызывают растяжение волокон, находящихся в первом квадранте).
Тогда формула для напряжений принимает вид:
Выражение показывает, что напряжения в точке линейно зависят
My
N Mx
z
y
x. от координат x, y. Для определения максимальных напряжений,
A Ix
Iy
необходимо найти точку, максимально удаленную от нулевой
(нейтральной оси).
y
Уравнение нулевой линии – Для получения уравнения нулевой линии
My
N Mx
+
достаточно приравнять напряжения нулю:
y
x 0. n
x0
A Ix
Iy
Нулевую линию можно построить с помощью отрезков,
x
отсекаемых этой прямой на координатных осях, которые
+
NI
y
NI x
определяются поочередным заданием нулевых значений
y
0
σ
max
H
x0
. y0
.
каждой из координат:
M A
M A
x
x
Mx
y
Таким образом, максимальное напряжение возникает в точке в правом верхнем углу
рассматриваемого прямоугольного поперечного сечения, которая наиболее удалена
от нулевой линии:
M
M
z
x
-
B
N Mx H
N M
y B
y
x
.
A Ix 2
I y 2 A Wx W y
Этот же результат для данного простого сечения можно получить
без нахождения положения нулевой линии, рассматривая знаки
My
слагаемых напряжений в угловых точках :
N Mx
z
A
Ix
y
Iy
n
+
-
x
N Mx My
.
A Wx W y
+
14
20. Лекция 7 (продолжение – 7.2)
■Косой изгиб – В частном случае, при отсутствии продольной силы (N =0) и одновременном действии изгибающих моментов Mx и My
сочетание двух прямых (плоских) изгибов вызывает косой изгиб.
My
Плоскость действия
Нормальные напряжения в произвольной точке сечения теперь определяется выражением: M x y
x.
полного момента M
z
Изобразим изгибающие моменты в виде векторов моментов пар сил, как это делалось
в теоретической механике, совпадающими по направлению с положительными направлениями осей:
Полный изгибающий момент есть векторная сумма этих векторов, модуль которого равен: M
Ix
Iy
y
β
M
M M ;
2
x
2
y
Напряжения в произвольной точке сечения можно
выразить через полный изгибающий момент:
z
Плоскость
действия
момента My
y cos x sin
My
Mx
M cos
M sin
.
y
x
y
x M
I
Iх
Iy
Ix
Iy
I
x
y
y cos x sin
0.
Ix
I
y
z M
x
Mx
H
B
y cos x sin
0.
Ix
Iy
Уравнение нейтральной линии представляет собой уравнение прямой, проходящей через начало координат.
Тангенс угла наклона (угловой коэффициент) равен:
M
n
Здесь учтено, что напряжения в первой четверти (x > 0 и y > 0) от изгибающего момента My отрицательны, поскольку
поворот плоскости поперечного сечения от этого момента происходит против часовой стрелки при взгляде навстречу вектору
момента и вызывает сжатие волокон в этой четверти.
Определим положение нейтральной линии,
задавая напряжения равными нулю:
β
у
Изгибающие моменты и полный момент связаны известными соотношениями:
M x M cos( M , x) M cos ; M y M cos( M , y ) M sin .
n
tg tg
Плоскость
действия
момента Mx
y tg
Ix
x.
Iy
Ix
.
Iy
В случае Ix > Iy, что обычно и бывает при проектировании балки, несущей преимущественно вертикальную
нагрузку, угол наклона нулевой линии больше угла наклона полного изгибающего момента . Это означает,
что полный прогиб не совпадает с плоскостью действия полного момента. Отсюда и происходит название косого изгиба.
Неприятность в том, что при малом отклонении, например, от вертикали расчетной нагрузки или отклонении от вертикали расчетного
положения сечения, происходит значительное увеличение напряжений в поперечном сечении и деформаций (прогибов) такой балки.
Пусть такое отклонение от вертикали поперечного двутаврового сечения балки №20 с моментами сопротивления Wx = 184 см3, Wy=23.1 см3,
с моментами инерции Ix = 1840 см4, Iy=115 см4 составляет всего 2о.
Максимальное напряжение при отклонении оказывается выше на 27.7% от расчетного значения (без отклонения по вертикали),
а максимальный прогиб – на 14.5%. Это можно посмотреть в документе MathCAD, в котором задаются единичные значения полного момента
и коэффициента пропорциональности прогиба. Полный прогиб вычисляется как геометрическая сумма прогибов в каждой из плоскостей:
15
21. Лекция 8
■Внецентренное растяжение-сжатие – Рассмотренная комбинация внутренних усилий может возникать при действии растягивающей или
сжимающей силы F, не совпадающей с осью стержня и имеющей некоторые смещения относительно центральных осей
(эксцентриситеты) xF и yF. При переносе силы параллельно самой себе в новый центр возникают моменты Mx и My присоединенных пар
(метод Пуансо):
Таким образом, в произвольном сечении стержня имеем внутренние усилия: N = - F; Mx = - F∙yF; My = - F∙xF.
и уравнение нулевой линии
F
принимает вид:
или с использованием
Mx
Fx F
F Fy F
радиусов инерции сечения:
y y x x
y
x 0
1 F2 F2 0. (1)
My
A
Ix
Iy
2
2
x
I x i x A; I y i y A.
F
yF
z
x
y
C
ix
iy
При проектировании массивных сжатых стоек из материалов, имеющих предел
прочности на растяжение значительно меньше чем на сжатие (бетон, кирпичная или бутовая кладка, чугун)
необходимо обеспечить в поперечном сечении отсутствие растягивающих напряжений, т.е. нулевая линия не
должна пересекать контур поперечного сечения. Таким образом, встает вопрос о допустимых смещениях сжимающей
силы относительно центральных осей поперечного сечения. Область допустимых положений продольной силы,
при которых во всем сечении возникают напряжения одного знака, называется ядром сечения.
■ Построение ядра сечения – Рассмотрим для простоты прямоугольное сечение размером bxh:
Радиусы инерции сечения:
y
Iy
HB 3
B2
I
BH 3
H2
n4
.
ix2 x
; i y2
n1
A
12 BH
12
A
12 BH
12
с n2
n1
Зададим положение нулевой линии по верхнему краю сечения и определим координаты точки
xF
с
3
приложения продольной силы, соответствующие этой нулевой линии:
Уравнение нулевой линии
(1) показывает, H
координаты точки приложения силы и координаты точки, в которой
Уравнение
H
4
Из уравнения внулевой
можно
определить
x
y
, x любое;выражающейся
напряжения обращаются
в
нуль,
обладают
“взаимностью”,
том, чтолинии
если силу
поместить
в
нулевой линии:
2
2
2
координаты
силы:
2
yF
любую точку найденной нулевой линии, то новая нулевая линия пройдет обязательно через точку,ixв которой
H 2
H
xF 0; yF
.
была ранее сила.
y
12 H
6
1
Следовательно при движении точки приложения силы по прямой, совпадающей с первоначальной нулевой
Зададим
положение
линии
правому
краюнулевая
сечениялиния
и определим
координатыпроходить
точки приложения
n3
n3
линией,
например,
по нулевой
верхнему
краюпо
сечения,
новая
будет продолжать
через ту же
продольной
силы,
соответствующие
этой
нулевой
линии:
2
2
точку, вращаясь вокруг нее, поскольку уравнение (1) остается в силе.
i
B
B 2
B
Уравнение нулевой линии:
B
n2
xF y
; y F 0.
x
,
y
любое
;
В системе MathCAD можно показать, что при повороте нулевой линии вокруг неподвижной
точки,
например,
x
12
B
6
n4
2
правого верхнего угла прямоугольного сечения, точка приложения силы перемещается по прямой из
Далее, повторяя это для двух остальных сторон сечения, получаем положения продольной силы. Полученные
положения 1 в положение 2 ( - угол наклона нулевой линии, с – произвольный отрезок нулевой линии).
точки являются вершинами ядра сечения.
Можно доказать, что при изменении положения точки приложения продольной силы нулевой линии по прямой,
соединяющей две вершины ядра сечения, нулевая линия, оставаясь касательной к контуру, лишь поворачивается, или
наоборот, при повороте нулевой линии вокруг угла сечения (n1-n1 переходит в n2-n2 ) точка приложения продольной силы
перемещается по прямой, соединяющей вершины 1 и 2:
16
22. Лекция 8 (продолжение – 8.2)
■■
■
Изгиб с кручением – При одновременном действии изгибающих моментов Mx и My и крутящего момента Mz в поперечном сечении возникают
как нормальные напряжения (от изгиба), так и касательные напряжения ( от кручения). Такое совместное действие испытывают оси
редукторов, валы двигателей, ведущие оси колесных пар локомотивов.
Для определения опасного сечения в таких элементах должны быть построены эпюры указанных внутренних усилий, включая в определенных
случаях эпюры поперечных сил.
В случае равенства моментов инерции относительно главных осей, что и имеет место для валов круглого сечения, при действии изгибающих
моментов в двух плоскостях косой изгиб не возникает. Изгибающие моменты Mx и My могут быть заменены одним (полным) изгибающим
моментом Mи. Аналогично и поперечные силы Qy и Qx приводятся к равнодействующей силе Q. Таким образом, брус круглого сечения
испытывает сочетание прямого (плоского) поперечного изгиба и кручения (при отсутствии продольной силы).
M
и
y. Касательные напряжения от кручения – по формуле:
■ Нормальные напряжения определяются по формуле и
Ix
отс
Касательные напряжения
QS
и y x .
от поперечной силы Здесь принимаем, что ось x совпадает с положением нулевой линии n-n.
I xb
y
Эп.σи
A
При расчете круглых валов опасные точки находятся на контуре поперечного сечения,
максимально удаленных от осей x и z, в которых одновременно достигают максимума
нормальные изгибные и касательные напряжения от кручения (касательные напряжения
x
n
от поперечной силы максимальны на оси x и равны нулю при y = ymax):
n
иmax
z
кр
и
и
Mи
.
Wx
крmax
M кр
W
.
кр
M кр
I
Эп. кр
.
Эп. и
B
При чистом кручении напряженным состоянием элементарного параллелепипеда является
Тогда условие прочности по III и IV теориям прочности можно записать
чистый сдвиг.
в виде одного выражения:
(I )
При наличии дополнительно изгиба напряженным
состоянием элементарного параллелепипеда
M экв
экв
R
является уже частный случай
плоского
напряженного
состояния ( y = 0).
Wx
Максимальные нормальные и касательные напряжения возникают в точках контура A и B.
( III )напряжения
2этих точках
( IV )
Главные
где
M экв
M и2 Mвкр
; M экв
определяются соотношениями:
2
2
- эквивалентные
M и2 0.75
M кр
иmax
2
иmax
max
и
по III кр
1,3
моменты
.
теориям
прочности
2
2
IV
При расчете на прочность необходимо воспользоваться одной из теорий прочности, рассматриваемых подробно в следующей лекции.
Условие прочности по III теории прочности для рассматриваемого напряженного состояния принимает вид:
2
2
Условие прочности по IV теории прочности:
2
max 2
иmax 3 кр
R.
Используя выражения для максимальных
нормальных и касательных напряжений и учитывая, что W =2Wx получаем:
4 R.
max
и
2
M и2 M кр
Wx
R и
2
M и2 0.75M кр
Wx
R.
max
кр
17
23. Лекция 8 (продолжение – 8.3)
Определение перемещений в пространственном стержне – В пространственном стержне в общем случае на каждом из участков могутвозникать различные комбинации внутренних усилий. Техника построения эпюр для пространственных ломаных стержней
рассматривалась в лекции 6.
Каждая точка оси бруса под действием приложенной нагрузки может иметь в общем случае три перемещения в пространстве (u, v и w). Кроме того,
поперечное сечения бруса может иметь три угла поворота относительно центральных осей. Таким образом, необходим общий метод
определения указанных перемещений. Таким методом является метод Максвелла-Мора, основанный на использовании вспомогательных
состояний, в которых задается единичное усилие (сила или момент-пара сил) по направлению искомого перемещения.
В самой общей форме перемещения с использованием интегралов Мора имеет вид:
■
n sk
M xi M xq ds
k 1 0
EI x
iq
n sk
M yi M yq ds
k 1 0
EI y
n sk
M zi M zq ds
k 1 0
GI z
n sk
Ni N q ds
k 1 0
EA
n sk
Qxi Qxq ds
k 1 0
GA
kx
n sk
Qyi Qyq ds
k 1 0
GA
ky
Здесь iq – любое перемещение (u,v, w, x, y, z),
M xi , M yi , M zi , Ni , Qxi , Qyi - выражения для внутренних усилий от единичного усилия, соответствующего искомому перемещению
по направлению и характеру (ед. сила или момент);
kx, ky – коэффициенты, зависящие от формы сечения:
2
A Sy
A S x2
k x 2 2 dA; k y 2 2 dA.
I y A bx
I x A by
Для прямоугольного сечения kx = ky = 1.2
Для круглого сечения kx = ky = 32/27 =1.185
В большинстве случаев при определении перемещений в балках, рамах и арках
влиянием продольных деформаций и сдвига пренебрегается и формула Мора
принимает вид:
n sk
M xi M xq ds
k 1 0
EI x
iq
n sk
M yi M yq ds
k 1 0
EI y
n sk
M zi M zq ds
k 1 0
GI z
a =1
y
.
x
A
На лекции 6 были построены эпюры изгибающих и крутящего моментов от нагрузки для
пространственного ломаного бруса.
Для определения, например, линейного перемещения центра поперечного сечения бруса,
расположенного на его конце по направлению силы F необходимо приложить в этой точке
по этому же направлению единичную силу P = 1 и построить соответствующие эпюры
изгибающих и крутящего моментов от этого воздействия.
y
c = 1.8
x
d = 0.8
y
z
y
z
x
x
z
M=qa2
q
z
b=1
x
y
F=qe z
e = 0.9
18
24. Лекция 8 (продолжение – 8.4)
a =1y
Пример определения перемещений в пространственном ломаном брусе –
С рассмотрением влияния деформаций только от изгиба и кручения перемещения
формула Мора имеет вид:
n sk M M ds
n sk M M ds
n sk M M ds
■
iq
k 1 0
xi
xq
EI x
k 1 0
yi
yq
EI y
k 1 0
zi
zq
GI z
A
y
.
z
-
Mx
My
-
0.1q
1.13q
1.93q
-
0.1q
+
0.81q
+
Mz
0.1q
0.
q
1.05q
-
0.81q
0.8q
-
Mx
My
0.9
0.9
1
1
+
0.9
-
+
0.9
-
P=1
P=1
q
z
b=1
x
y
F=qe z
e = 0.9
Задавая геометрические
характеристики поперечного
сечения (форма, размеры,
моменты инерции) и модули
упругости, вычислим сумму
интегралов Мора
с использованием правила
Верещагина, формул
трапеций и парабол:
0.9
Mz
+ 1
x
Для определения
перемещения конца бруса
по направлению силы F
приложим единичную
силу P=1 в этом
направлении:
P=1
0.8q
1.93q
-
0.9
x
+
Построим эпюры изгибающих и крутящего моментов от действия силы P=1:
0.9
c = 1.8
x
d = 0.8
y
z
M=qa2
1.93q
1.93q
0.8q
y
z
Ранее были построены для ломаного пространственного бруса эпюры изгибающих и крутящих
моментов от действия показанной нагрузки:
2.73q
x
P=1
Подобным же образом можно вычислить любое другое перемещение этого или иного поперечного сечения. Для каждого из них необходимо
выбрать соответствующее единичное нагружение, построить единичные эпюры и “перемножить” грузовые и единичные эпюры.
19
25. Лекция 9
Общие понятия о теориях прочности – При испытаниях материалов статической нагрузкой на центральное растяжение (сжатие) достигаетсяпредельное состояние, характеризуемое наступлением текучести, появлением значительных остаточных деформаций и/или трещин. Для
пластичным материалов за предельную или опасную величину напряжений принимается предел текучести Т, для хрупких – предел
прочности В.
При эксплуатации конструкций в общем случае по площадкам элементарного объема возникают нормальные и касательные
напряжения, пропорциональные увеличению нагрузки. Значение каждого из напряжений зависят от ориентации
рассматриваемых площадок.
Вариацией углов поворота площадок можно определить площадки, свободные от касательных напряжений, на которых
yz σy
возникают максимальные нормальные напряжения. Такие площадки и напряжения называются главными (способы их
yx
y zy
определения для плоского напряженного состояния были рассмотрены на лекции 9 первой части курса).
xy
σz
Именно главные напряжения и могут служить объективной характеристикой напряженного состояния в точке, поскольку
они являются инвариантами – величинами, независящими от ориентации площадок. В итоге при оценке прочности
zx
xz σ
z
материала вместо рассмотрения 9 компонент напряженного состояния, зависящих от ориентации элементарных
x
площадок, можно рассматривать всего 3 ( 1> 2> 3).
■
x
σ2
σ3
σ2
σ1
σ3
σz
При работе конструкции под нагрузкой некоторые точки находятся в условиях плоского или пространственного
напряженного состояния, для которых возможны самые различные соотношения между главными напряжениями. Для
определения предельного (опасного) состояния в точке (и тем самым всей конструкции), следовало бы сравнить эти
σ1 напряжения с предельными. Однако, практически это сделать невозможно, поскольку провести эксперименты,
подобные испытаниям на центральное растяжение-сжатие до разрушения, пришлось бы сделать для каждого из
возможных соотношений между главными напряжениями, не говоря уже о том, что реализовать эти соотношения при
испытаниях технически трудно.
Таким образом, необходимо иметь возможность сопоставить прочность материала при плоском и
пространственном напряженном состоянии с результатами испытаний при одноосном растяжении-сжатии.
Эта задача решается с помощью выдвижения гипотезы о каком-то одном критерии, определяющим условие
перехода материала в опасное состояние, составляющим основу соответствующей теории прочности.
σz С использованием того или иного критерия главные напряжения, возникающие в конструкции, удается связать с
предельными механическими характеристиками, получаемыми при одноосном испытании. В результате определяется
некоторое эквивалентное напряжение, характеризующее рассматриваемое напряженное состояние, которое можно
сравнивать с предельным или допускаемым напряжением при одноосном растяжении-сжатии.
■
Критерий разрушения путем отрыва (хрупкое разрушение) – Возможно частичное или полное разрушение тела. Различают разрушение
вязкое и хрупкое, которое могут проявляться как одновременно, так и последовательно. Хрупкое разрушение происходит в результате быстрого
распространения трещины после незначительной пластической деформации или без нее. В последнем случае разрушение называется идеально
хрупким. При хрупком разрушении скорость распространения трещины велика (0,2-0,5 скорости звука), а излом имеет кристаллический вид. При
квазихрупком разрушении наблюдается некоторая пластическая зона перед краем трещины. Хрупкие трещины могут возникать при средних
напряжениях, не превышающих предел текучести. Часто трещины медленно растут и процесс их роста может составлять до 90% времени
20
“жизни” детали. Поэтому имеет значение не столько факт возникновения трещины, сколько темп ее роста.
26. Лекция 9 (продолжение – 9.2)
Поля нормальных и касательных напряжений у вершины трещины описываются некоторыми функциями,полученные методами теории упругости, в которые входит коэффициент интенсивности напряжений,
имеющий различные значения в зависимости от типа деформации трещин:
I – трещина нормального отрыва;
II – трещина плоского сдвига;
III – трещина антиплоского сдвига.
Ниже рассматриваемые три теории прочности основываются на критерии разрушения путем отрыва.
I теория прочности - Теория наибольших нормальных напряжений: гипотеза перехода материала в опасное состояние –
достижение одного из главных напряжений предельного (опасного) значения.
С использованием этого критерия
экв 1 R - при 1 3
условие прочности имеет вид:
Первое условие используется при 1> 2> 3 > 0,
второе – при 3 < 0, если | 3| > | 1|
- при
экв 3 R
1
3
Теория учитывает лишь одно из главных напряжений, экспериментально подтверждается лишь для хрупких материалов при условии,
что одно из главных напряжений значительно больше других.
II Теория прочности - Теория наибольших деформаций: гипотеза перехода материала в опасное состояние – достижение
деформациями предельного (опасного) значения.
Здесь при вычислении максимальной деформации участвуют все три главные
С использованием этого критерия
напряжения:
условие прочности имеет вид:
o .
max
o
E
Следовательно, условие прочности,
выраженное через главные напряжения принимает вид:
max
1
1 ( 2 3 ) .
E
экв 1 ( 2 3 ) R.
Теория учитывает все три главные напряжения, но экспериментально подтверждается лишь для хрупких материалов при условии,
что все главные напряжения отрицательны.
Таким образом, I и II вторая теории могут применяться лишь для хрупких материалов. Заметим, что хрупкие материалы часто обладают
различными механическими характеристиками при растяжении и сжатии, Поэтому в этих случаях необходимо использовать
соответствующие расчетные (допускаемые) напряжения.
Теория прочности Мора – использует предположение, что напряжение 2 мало влияет на прочность материала (в пределах 15%). Таким
образом расчет прочности в общем случае трехосного напряженного состояния сводится к расчету прочности при двухосном напряженном
состоянии.
Это не означает, что в условии для II теории просто следует приравнять 2 нулю. Здесь расчетное напряжение определяется с учетом двух
испытаний: на растяжение - р и на сжатие - с.
21
27. Лекция 9 (продолжение – 9.3)
Суть теории Мора в следующем: Пусть известны данные об опасных состояниях материала при нескольких различных соотношениях междунапряжениями 3 и 1. Изображая каждое из состояний кругами Мора получим некоторое семейство таких кругов:
для двухосного напряженного состояния – круги черного цвета;
Одноосное
для одноосных растяжения и сжатия – круги красного цвета;
сжатие
+
для чистого сдвига – круг синего цвета.
Для материалов, сопротивление которых при сжатии больше, чем при растяжении, огибающая
Одноосное
растяжение
предельных напряжений (пунктирная кривая) приближается к положительной оси абсцисс
и пересекает ее в точке A, соответствующей двухосевому равномерному растяжению.
Эксперименты показывают, что при всестороннем сжатии материал не разрушается при любых,
-
A +
сколь угодно больших напряжениях. Поэтому огибающая не пересекает ось абсцисс при сжимающих
напряжениях.
Уменьшая круги предельных напряжений в n раз (n – коэффициент запаса) получим область,
соответствующую допускаемым (безопасным) напряженным состояниям:
-
Двухосное
напряженное
состояние
(сжатие)
Двухосное
напряженное
состояние
(растяжение)
Чистый
сдвиг
+
Поскольку получить достаточно большое количество опытных данных затруднительно, обычно
ограничиваются лишь двумя испытаниями ( на растяжение и на сжатие) и огибающие кривые
заменяют прямыми, касательными к кругам Мора, построенным по этим испытаниям:
Для такой упрощенной диаграммы предельных напряженных состояний возможно получить
аналитическое условие прочности из подобия прямоугольных треугольников:
0.5 с 0.5 р
+
-
A
0.5 с 0.5 р
0.5 р 0.5 1 3
0.5 1 3 0.5 р
Сократим на 0.5 и перемножим:
р c 1 c 3 c р 2 1 р 3 р
с
р
3
Теория Мора хорошо
согласуется
с экспериментальными
данными
при σ1> 0, σ3< 0.
Недостатком теории
Мора является неучет
промежуточного главного
напряжения σ2.
1 c 3 c р c 1 р 3 р р 2
1
0.5 с
После сокращения, сложения и сокращения
на 2 получим:
р c 1 c 3 р 0
0.5 р
0.5( 3- 1)
0.5 с-0.5 р
0.5 р
0.5 с
0.5( 3+ 1)
Отсюда соотношение, удовлетворяющее линии
предельных циклов:
Следовательно, условие
прочности имеет вид:
1 3
экв 1 3
р
c
р.
р
р.
с
22
28. Лекция 10
Критерий пластического состояния – При испытаниях материалов было обнаружено, что в пластическом состоянии максимальноекасательное напряжение имеет одно и то же значение для данного материала. В результате в качестве следующей гипотезы перехода
материала в предельное состояние можно выбрать достижение наибольших касательных напряжений предельного (опасного)
значения (критерий пластичности). Эта гипотеза легла в основу III теории прочности.
С использованием этого критерия
3 0 Т
условие прочности имеет вид:
1
■
max
В случае плоского
напряженного состояния:
1
3
x y
2
x y
2
2
2
2
1
2
( x y ) 2 4 yx
.
2
1
2
( x y ) 2 4 yx
.
2
экв
1
3
Т
2
экв ( x y ) 2 4 yx
Т
При изгибе с кручением:
2
экв и2 4 кр
R
Экспериментальные данные показывают хорошее совпадение результатов для пластичных материалов. Недостатком III теории по-прежнему
является неучет среднего главного напряжения 2 .
■
IV теория прочности (энергетическая) – Первоначальной попыткой связать все три главных напряжения было выдвижение гипотезы
перехода в предельное состояние удельной потенциальной энергии деформации некоторого предельного значения. Эксперименты
показали, что при всестороннем сжатии пластические деформации не возникают, хотя при этом накапливается большая удельная
потенциальная энергия. В связи с этим была выдвинута гипотеза о том, что предельное состояние обуславливается достижением
предельного значения лишь той части удельной потенциальной энергии деформации, которая связана с изменением формы:
u ф u u об ,
где u
1
( 1 1 2 2 3 3 ) - полная удельная потенциальная энергия.
2
Подстановка обобщенного закона Гука
дает следующее выражение для полной удельной
1
u
( 12 22 32 2 ( 1 2 2 3 3 1 ))
потенциальной энергии:
2E
Удельную потенциальную энергию, затрачиваемую
на изменение объема, можно получить из этого
(1 2 ) 2
выражения, полагая 1 = 2 = 3= о:
u об
3 0 .
2E
u об
1
[ 1 ( 2 3 )];
E
1
2 [ 2 ( 1 3 )];
E
1
3 [ 3 ( 1 2 )].
E
1
(1 2 )
( 1 2 3 ) 2 .
6E
1
3
1
(1 2 )
Удельная потенциальная энергия,
u u u об
( 12 22 32 2 ( 1 2 2 3 3 1 ))
( 1 2 3 ) 2 .
затрачиваемая на изменение формы: ф
2E
6E
Примем:
o ср ( 1 2 3 )
23
29. Лекция 10 (продолжение – 10.2)
Полученное выражение u ф1
(1 2 )
( 12 22 32 2 ( 1 2 2 3 3 1 ))
( 1 2 3 ) 2 .
2E
6E
после приведения к общему знаменателю, раскрытия квадрата суммы,
умножения и вычитания дает:
1
uф
3E
( 12 22 32 1 2 2 3 3 1 ) или
uф
1
(( 1 2 ) 2 ( 2 3 ) 2 ( 3 1 ) 2 )
6E
Замечание: Эти же соотношения можно получить непосредственно
1
из выражения для полной удельной энергии деформации
u
( 12 22 32 2 ( 1 2 2 3 3 1 )),
2E
задавая по главным площадкам напряжения, равные разности действующих главных напряжений и среднего напряжения: 1’ = 1 - о,
2’ = 2 - о, 3’ = 3 - о:
1
uф
2E
(( 1 o ) 2 ( 2 o ) 2 ( 3 o ) 2 2 (( 1 o )( 2 o ) ( 2 o )( 3 o ) ( 3 o )( 1 o ))
и подставляя значение среднего напряжения:
1
3
o ср ( 1 2 3 ).
Для одноосного растяжения при наступлении текучести 1 = Т , 2 = 3 = 0 удельная потенциальная энергия
составляет величину:
1 2
Приравнивая выражения удельной потенциальной энергии изменения формы для трехосного
uф
Т.
3E
напряженного состояния и для одноосного, получаем эквивалентное напряжение:
экв 12 22 32 1 2 2 3 3 1 Т
При изгибе с кручением:
или
экв
1
(( 1 2 ) 2 ( 2 3 ) 2 ( 3 1 ) 2 ) Т
2
экв и2 3 кр2 R
Как и теория III, энергетическая теория показывает хорошее совпадение результатов
с экспериментальными данными для пластичных материалов.
■
Понятия о новых теориях прочности и механики разрушения – Предельная поверхность, соответствующая условию появления массовых
пластических деформаций по IV теории, определяется уравнением:
( 1 2 ) 2 ( 2 3 ) 2 ( 3 1 ) 2 2 Т 0.
Уравнение соответствует поверхности
2
r
Т , ось которого равно наклонена к координатным осям 1, 2 и 3.
кругового цилиндра радиуса
3
Критерий, использованный в III теории дает поверхность правильной шестигранной призмы, вписанной в цилиндр, т.е. предельная область почти
совпадает с областью по IV теории. Критерий наибольших нормальных напряжений (I теория) дает куб с ребрами, равными о.
Новейшие теории прочности основываются на выборе различных вариантов предельной поверхности f( 1, 2, 3) = 0, при которой наиболее полно
можно учесть особенности сопротивления данного класса материалов в условиях сложного напряженного состояния. Например, в композитных
(армированных) материалах разрушение может частично происходить за счет разрыва волокон, а частично за счет скалывания матрицы.
В случае ортотропных материалов, имеющих различные пределы прочности, или материалов имеющие различные пределы прочности при сжатии
и растяжении условия прочности содержат константы, определяемые из соответствующих испытаний, т.е. используется не одно расчетное
сопротивление, а два и больше.
24
30. Лекция 10 (продолжение – 10.3)
■ Механика разрушения – относительно новое направление развитие теории прочности, в котором изучаются вопросы роста и устойчивоститрещин в элементах конструкций в зависимости от уровня нагружения и других условий в процессе эксплуатации. Обследования
эксплуатируемых металлических конструкций (мостов, газопроводов и резервуаров, корпусов кораблей и т.д.) показывают, что в их материале
всегда присутствуют дефекты типа пустот и трещин. При этом их поведение (стабилизация, медленный или быстрый рост) может различаться
в зависимости от их длины, формы, вида напряженного состояния и других факторов, например, толщины пластины, формы тела, граничных
условий.
При исследовании напряженного состояния конструкции, имеющей трещины, наибольший интерес представляет окрестность вершины трещины,
в которой возникают сверхвысокие напряжения. Методами теории упругости получено теоретическое распределение поля напряжений для
некоторых частных случаев, например, при сквозной трещине типа I (отрыв) длиной 2l в бесконечной пластине единичной толщины под действием
растягивающего напряжения σ. В элементе dxdy, расположенного на расстоянии r от вершины трещины и составляющий с плоскостью трещины
угол θ, напряжения в окрестности вершины трещины определяются уравнениями:
σ
y
x
r
σ
θ
x
2l
σ
l
3
l
3
l
3
cos 1 sin sin
cos 1 sin sin
sin cos cos .
; y
; xy
2r
2
2
2
2r
2
2
2
2r
2
2
2
В этих уравнениях присутствует сингулярный сомножитель, содержащий расстояние до вершины r, который
обращает напряжения в бесконечность при устремлении этого расстояния к нулю.
Уравнения могут быть представлены в обобщенном виде как
KI
ij
f ij ( ), где K l .
I
2 r
Коэффициент KI называется коэффициентом интенсивности напряжений (КИН). КИН полностью определяет
поле напряжений при вершине трещины.
KI
В частности для точек, лежащих на оси x (на продолжении трещины): y x
2 r
σ
y
Наличие сингулярного множителя в полученном упругом решении показывает, что при любом значении
растягивающего напряжения σ напряжения σy у вершины трещины (r = 0) могут быть сколь угодно большими
и это уже должно означать опасное состояние трещины. Однако, благодаря пластическим свойствам материала,
у острия трещины возникает зона пластических деформаций на участке 0 ≤ r ≤ rp, в которой напряжение
не превышает предела текучести σТ .
Размер этой зоны зависит от вида напряженного состояния (плоская деформация – толстые пластины или
плоское напряженное – тонкие пластины). При плоской деформации этот размер значительно меньше, но
он увеличивается до размера, соответствующему плоскому напряженному состоянию, при выходе трещины
на поверхность, поскольку на ней всегда существует именно плоское напряженное состояние.
σТ
rp
x
r
25
31. Лекция 10 (продолжение – 10.4)
Таким образом, интенсивность поля напряжений в окрестности вершины контролируется единственным параметром K, являющимся функциейтолько характера внешнего нагружения, геометрии пластины и размеров трещины. Для трещин другого расположения или пластин ограниченной
толщины КИНы записываются с некоторыми поправочными коэффициентами в виде:
K I f I l ; K II f II l ; K III f III l .
Например, для односторонней трещины fI = 1,12.
В теории разрушения используется гипотеза, подобная гипотезам в теориях прочности: причиной роста трещины является достижение
некоторой величины, в данном случае КИН, своего предельного (критического) значения. Критический КИН представляет собой силовой
критерий разрушения. Его иногда называют вязкостью разрушения. Возможны и другие критерии разрушения, в которых используется
непосредственно критическая длина трещины или критическое значение интенсивности освобождающейся упругой энергии деформации.
В частности, Гриффитс рассмотрел изменение потенциальной энергии деформации U пластины в связи с
U
W
продвижением трещины, при котором затрачивается работа A на образование новой свободной поверхности.
В начальной стадии развития трещины энергия поглощается dA > dU, затем энергия высвобождается dA < dU.
Энергетическое условие быстрого роста трещины по Гриффитсу: dA ≤ dU. Здесь:
A
dA Rdl , где R – константа, называемая сопротивлением росту трещины, связанная с плотностью энергии
образования свободной поверхности g, характеризуемой работой на разрушение межатомных
связей на единицу новой поверхности.
dU Gdl, где G – переменная величина, называемая скоростью
2 l
Высвобождение
высвобождения упругой энергии деформации, зависящая от длины трещины и равная G
.
энергии
Эту величину можно связать с КИН. Для плоского напряженного состояния:
l
E
KI
l
Таким образом, эти два критерия (силовой и энергетический) связаны между собой
K I2
полученным соотношением. При достижении одного из них критического значения, второй
W A U
G
.
также достигает своего критического значения, т.е. они эквивалентны и выполняются
E
одновременно.
Для плоского деформированного состояния соотношение
(1 2 ) K I2
2
G
.
дополняется коэффициентом (1 – μ ):
E
Теперь можно записать условие устойчивости (недопущения быстрого
K Ic
кр
.
распространения трещины) как G < Gc – критического значения скорости
l кр Величина KIc – критического коэффициента
освобождения энергии или KI < KIc – критического коэффициента
интенсивности определяется экспериментально
интенсивности.
на стандартизованных образцах: предварительно
Например, для плоского напряженного состояния:
кр
выращивается усталостная трещина, при
K Ic
l кр
кр
.
l K Ic
увеличении нагрузки регистрируется ее величина
lкр
в момент хрупкого разрушения, для которой
затем вычисляется KIc.
Поглощение
энергии
25
32. Лекция 10 (продолжение – 10.5)
Более подробно о механике разрушения см. [1], а также [5] и Д. Броек “Основы механики разрушения”. Последняя книга доступна для чтенияна сайте http://mysopromat.ru/uchebnye_kursy/mehanika_razrusheniya.
Замечание: на стр. 24 книги Д. Броека в формуле (1.12) допущены опечатки. Правильно см. здесь на стр. 25.
Продолжение и окончание предложенного вашему вниманию курса находится
(http://www.miit.ru/institut/ipss/faculties/stm/main.htm), т.е. там же, откуда вы взяли эту часть курса. Желаю успеха.
26



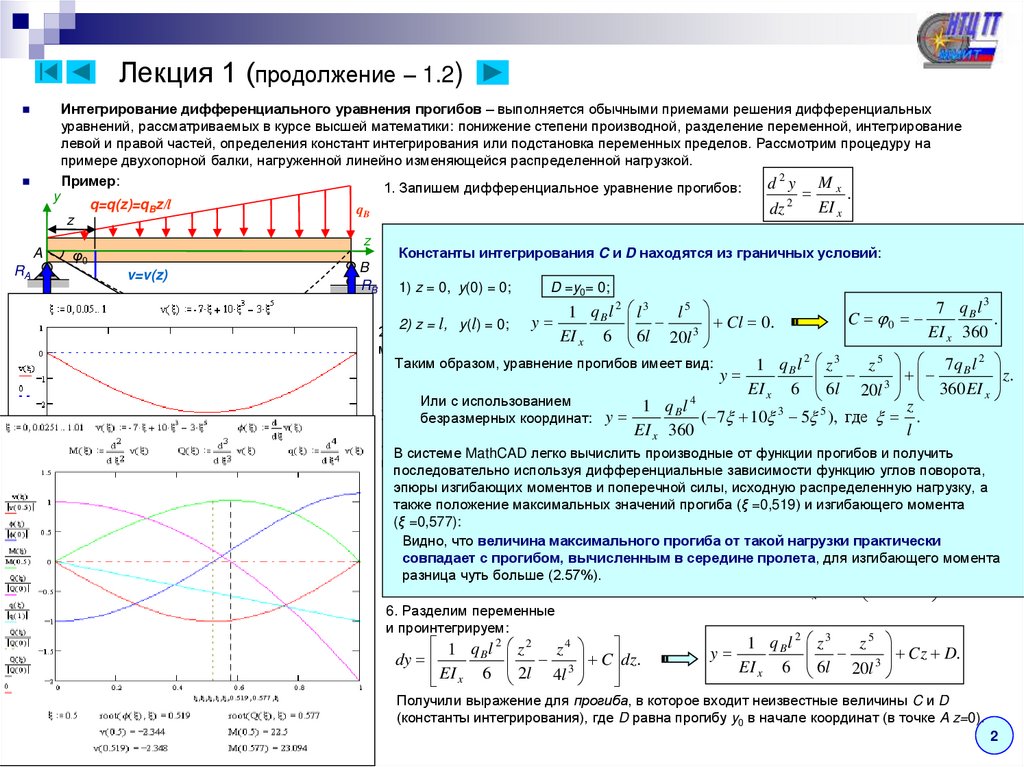

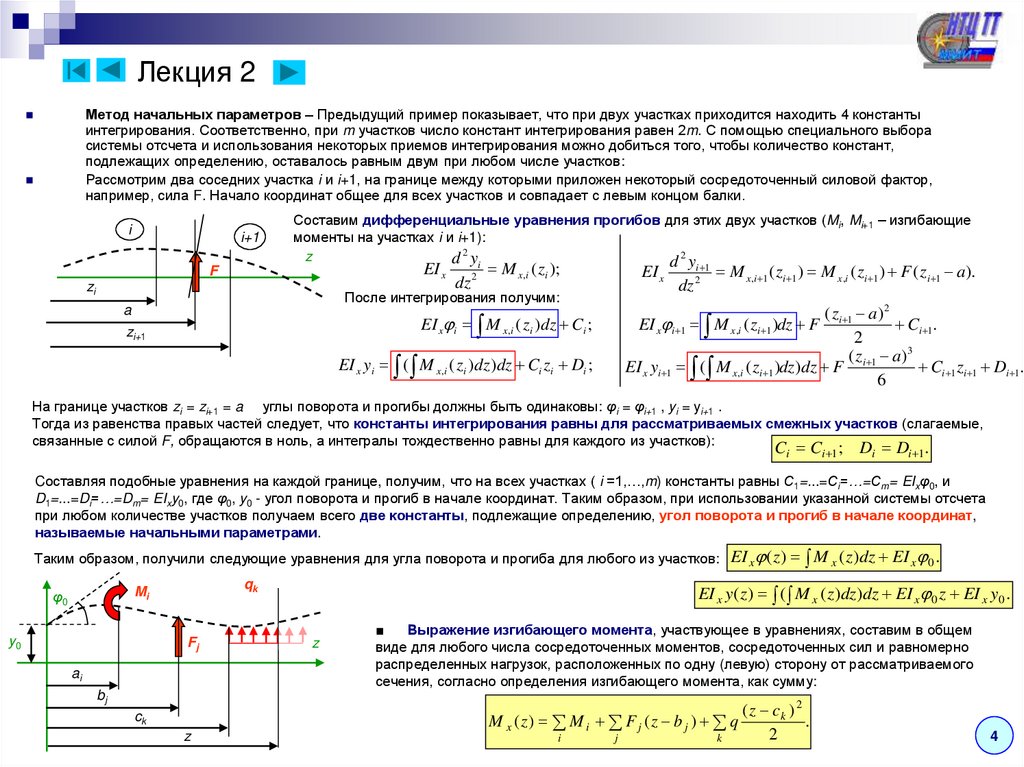

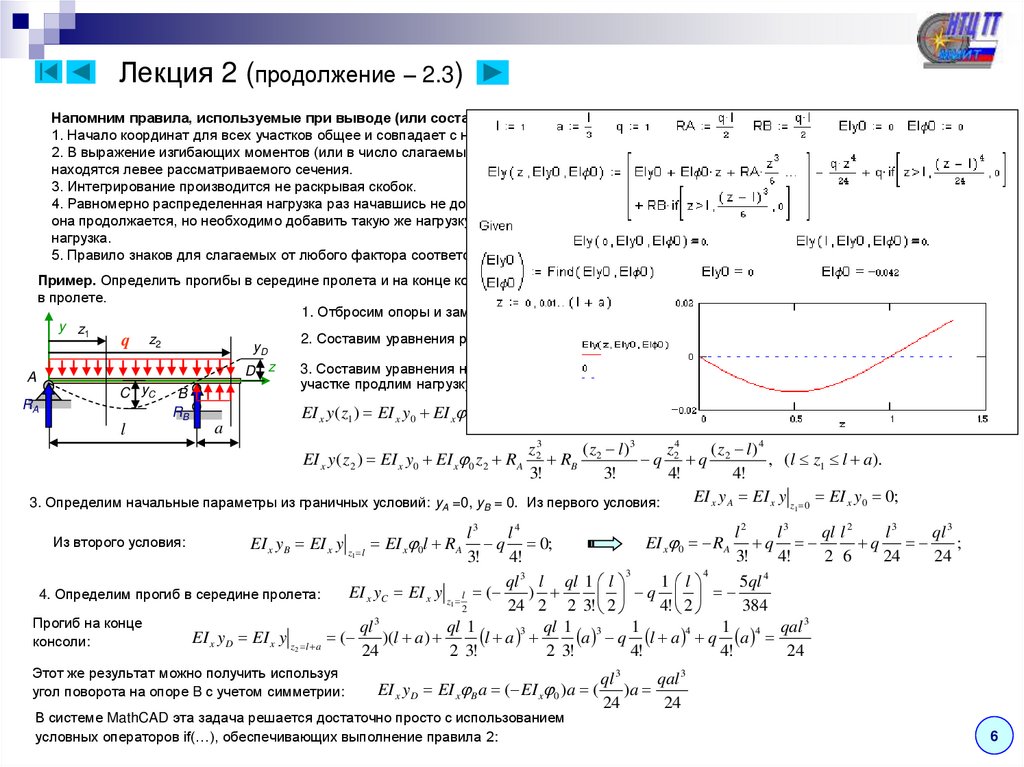








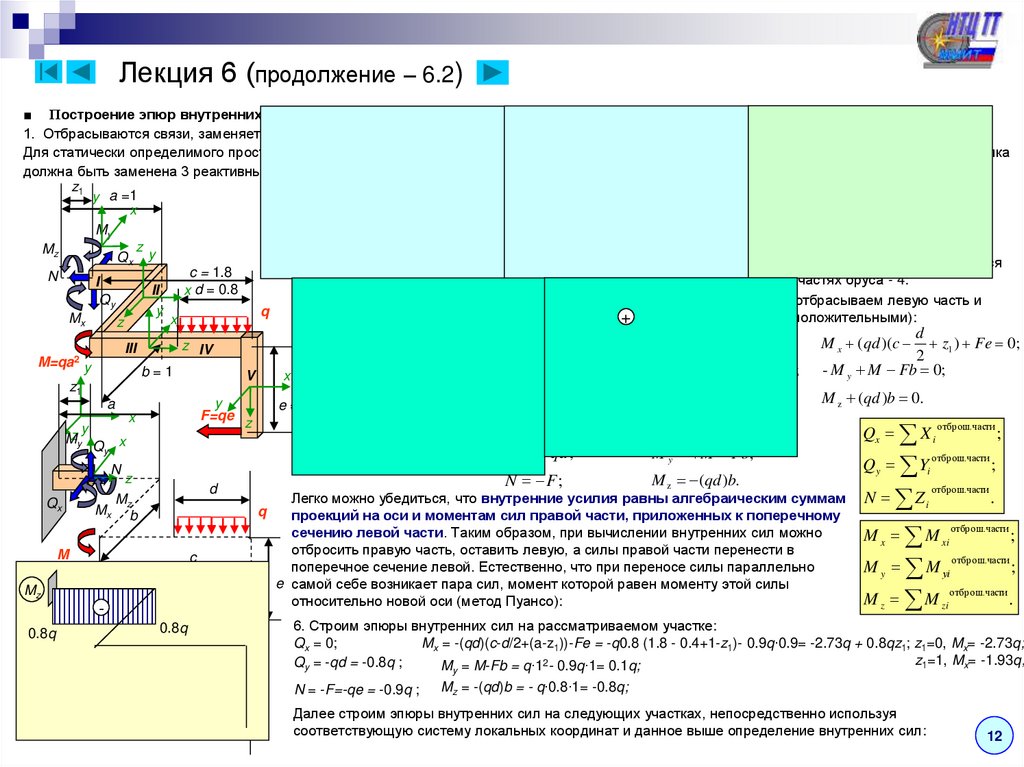
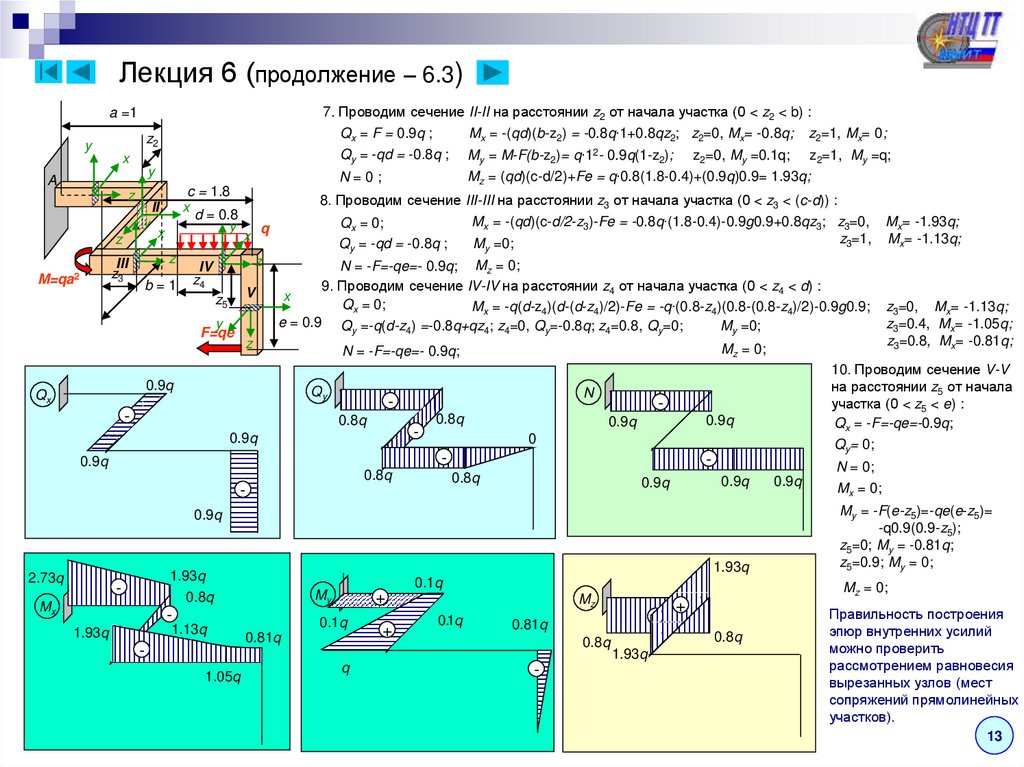
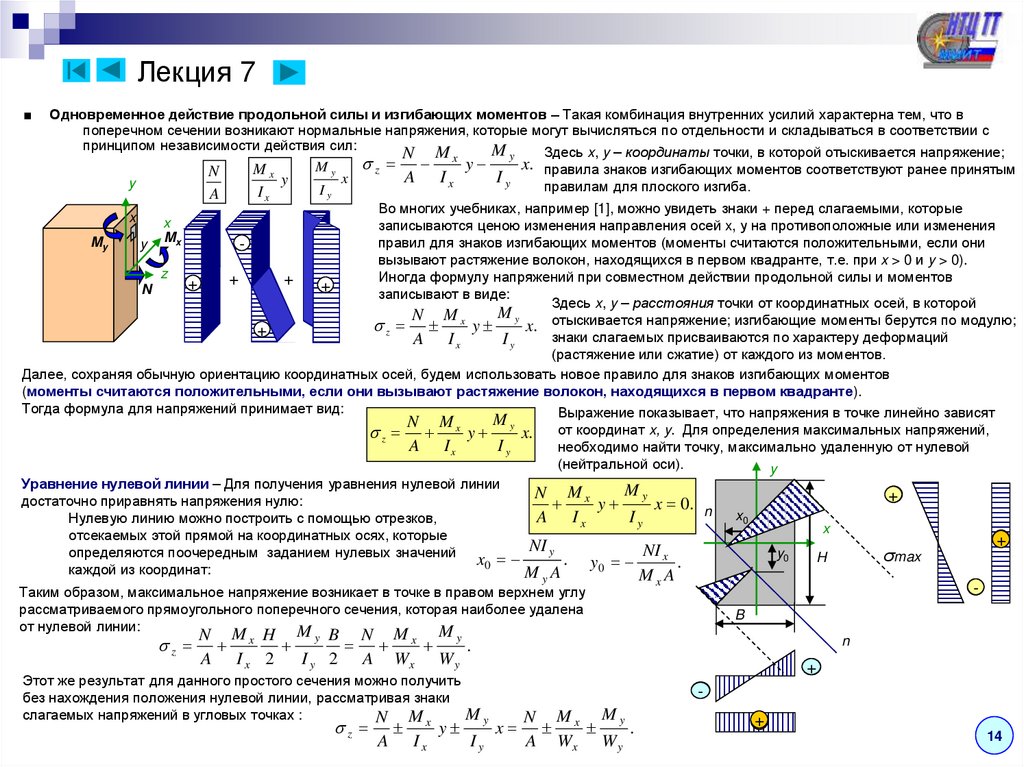

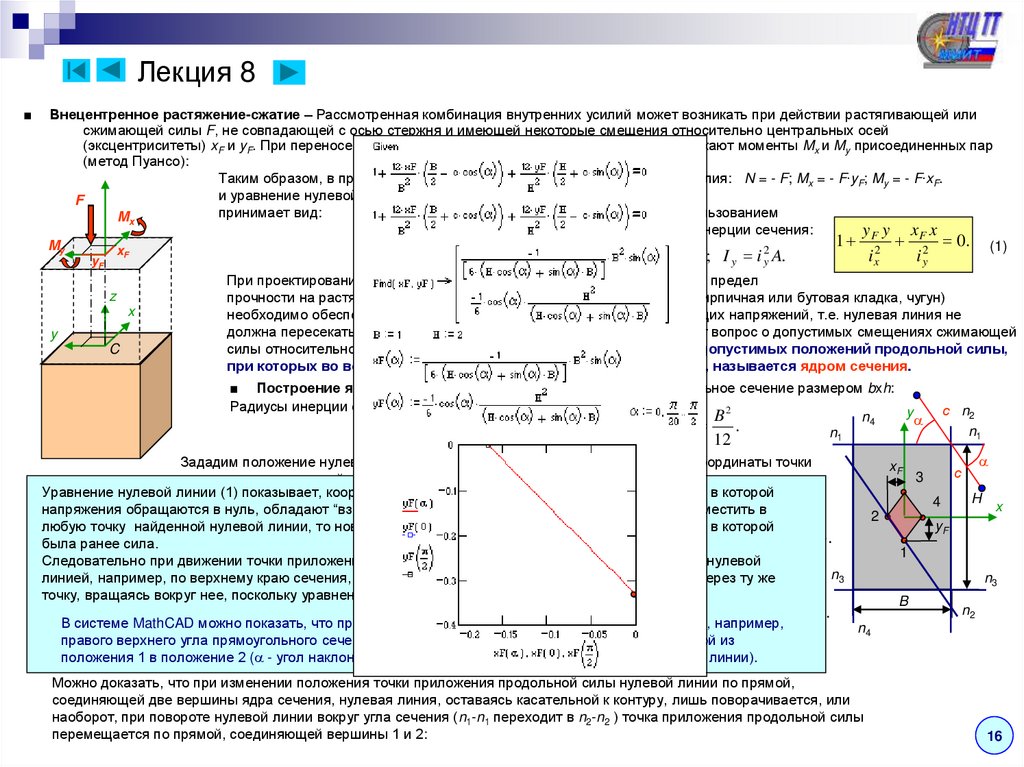


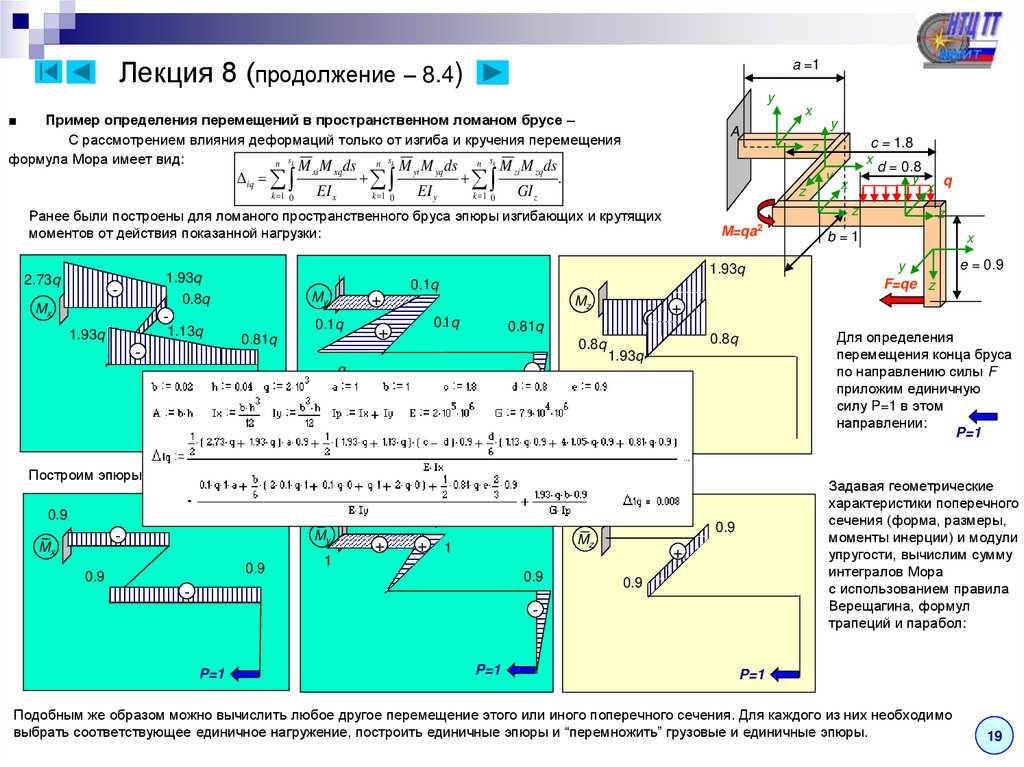





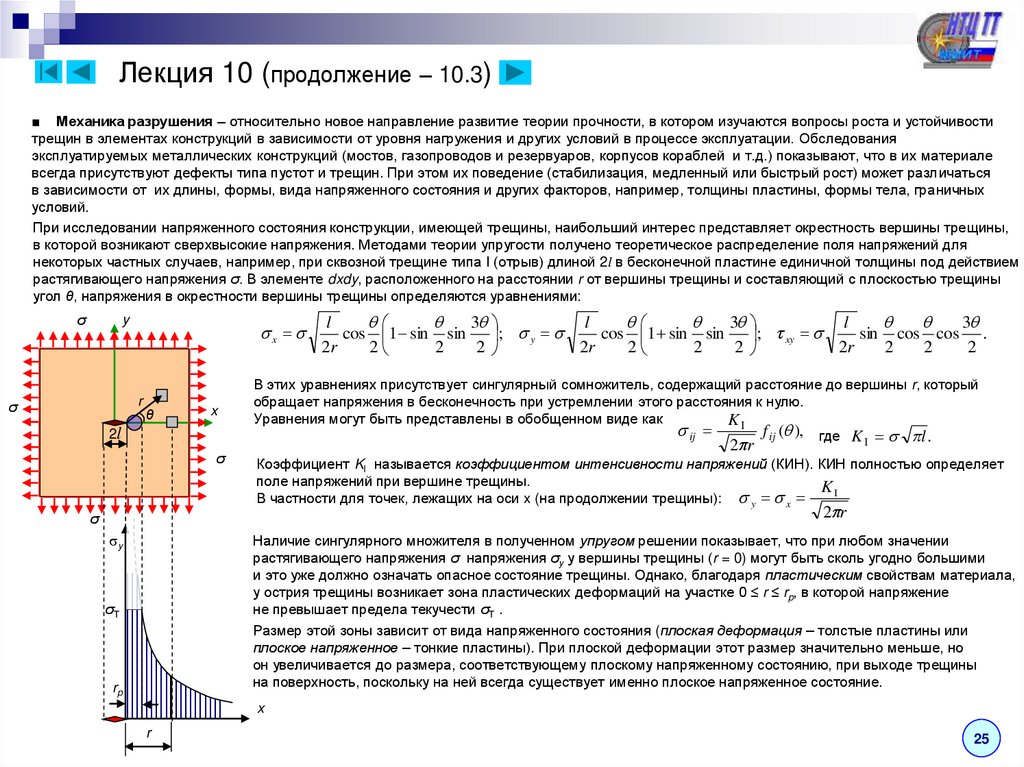
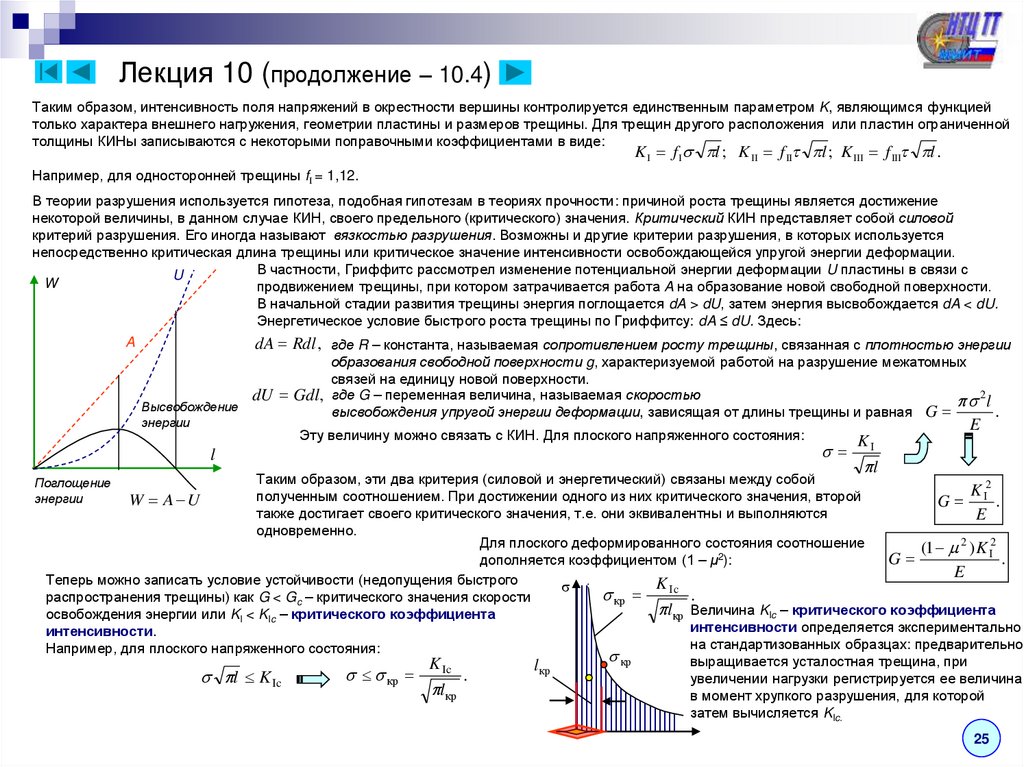
 Механика
Механика








