Алгоритмы работы со стеками

1.

Алгоритмы работы со стеками
Проверка корректности расстановки скобок
Во многих случаях стек является удобной промежуточной структурой данных для хранения
информации во время работы алгоритма. Простой пример.
Пусть требуется проверить правильность расстановки скобок в некотором тексте. Если скобки
только одного вида, то задачу можно решить простым подсчетом скобок.
(x * (1+3*(x+y)) – 1) * (x-1)
public static boolean correct(String src) {
int count = 0;
for (char c : src.toCharArray()) {
if (c == '(') {
count++;
} else if (c == ')') {
if (--count < 0) return false;
}
}
return count == 0;
}
В общем случае этого недостаточно.
int [] a = { f(3), arr[g(5)], (int[]{ 1, 2, 3 })[1] }
Кубенский А.А. Дискретная математика.

2.

Проверка корректности расстановки скобок
Будем класть в стек закрывающую скобку каждый раз, когда встретится в тексте открывающая
скобка соответствующего вида.
Когда будет встречаться закрывающая скобка, будем проверять, находится ли в стеке
правильный символ закрывающей скобки.
public static boolean correctParentheses(String src) {
Stack<Character> stack = new StackImpl<>();
for (char c : src.toCharArray()) {
switch (c) {
case '(': stack.push(')'); break;
case '[': stack.push(']'); break;
case '{': stack.push('}'); break;
case ')': case ']': case '}':
if (stack.isEmpty()) return false; else
if (c != stack.pop()) return false;
break;
}
}
return stack.isEmpty();
}
Кубенский А.А. Дискретная математика.

3.

Проверка корректности расстановки скобок
Можно передавать в функцию строку, содержащую все правильные пары скобок, тогда функция
проверки приобретает следующий вид:
public static boolean correctParentheses(String src, String parentheses) {
Stack<Character> stack = new StackImpl<>();
for (char c : src.toCharArray()) {
int index = parentheses.indexOf(c);
if ((index & 1) == 0) { // open bracket
stack.push(parentheses.charAt(index + 1));
} else if (index > 0) { // close bracket
if (stack.isEmpty()) return false;
else if (c != stack.pop()) return false;
}
}
return stack.isEmpty();
}
Кубенский А.А. Дискретная математика.

4.

Обратная польская запись
Привычная нам запись выражений с инфиксными операциями и скобками не слишком удобна
для обработки. Не так-то просто написать программу, которая будет вычислять значение
выражения по его записи (12 * (1+3*(7+2)) – 1) * (11-1)
В постфиксной записи операция ставится после операндов. Рассмотрим, например, запись
12 1 3 7 2 + * + * 1 – 11 1 - *
Она не похожа на исходное выражение, но анализируется и вычисляется гораздо проще.
Дополнительное преимущество – при такой записи не надо знать про приоритеты операций (но
надо знать, какое число операндов требует операция).
Вычислительный алгоритм будет складывать в стек числа по мере того, как они появляются в
исходной строке, и будет выполнять операции над числами на вершине стека, если встречается
знак операции.
12
12
12
12
12
12
12
12
1
1
1
1
1
1
28
3
3
3
3
27
7
7
9
2
Кубенский А.А. Дискретная математика.
336
336
1
335
335
335
335
11
11
10
1
3350

5.

Обратная польская запись
public static int calculate(String polish) {
String[] p = polish.split("\\s+");
Stack<Integer> stack = new StackImpl<>();
for (String obj : p) {
try {
int n = Integer.parseInt(obj);
stack.push(n);
} catch (NumberFormatException e) {
// operator
int operand2 = stack.pop();
int operand1 = stack.pop();
stack.push(execute(operand1, obj, operand2));
}
}
return stack.pop();
}
private static int execute(int operand1, String obj, int operand2) {
switch (obj) {
case "+": return operand1 + operand2;
case "-": return operand1 - operand2;
case "*": return operand1 * operand2;
}
return 0;
}
Кубенский А.А. Дискретная математика.

6.

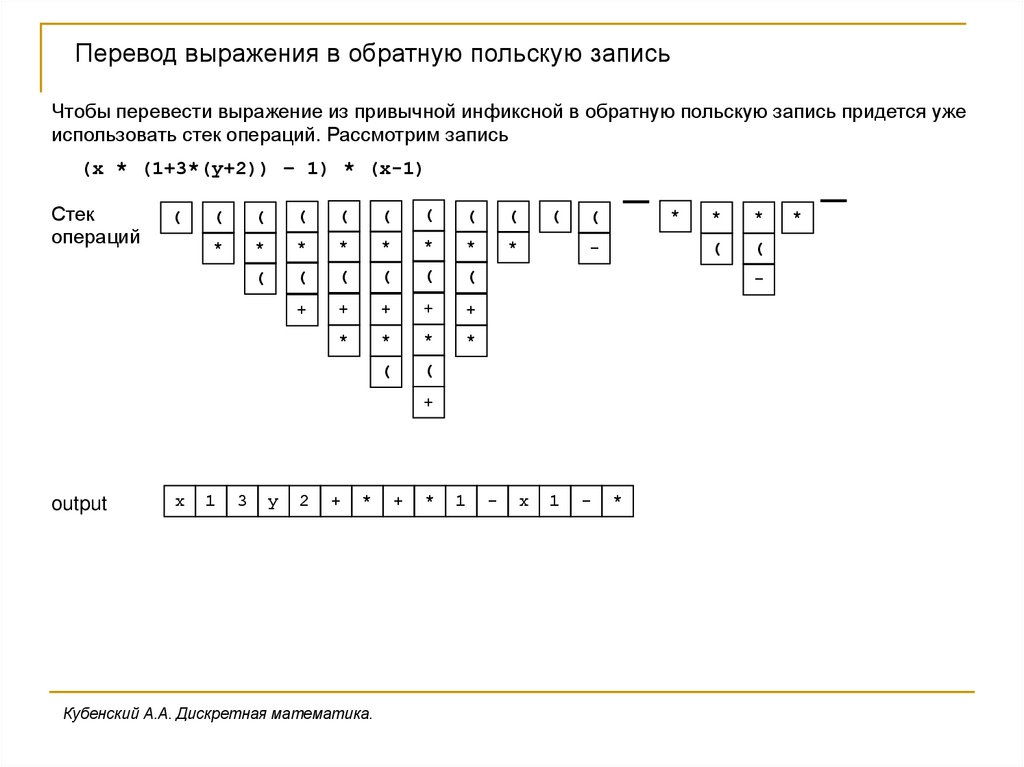
Перевод выражения в обратную польскую запись
Чтобы перевести выражение из привычной инфиксной в обратную польскую запись придется уже
использовать стек операций. Рассмотрим запись
(x * (1+3*(y+2)) – 1) * (x-1)
Стек
операций
(
(
(
(
(
(
(
(
(
*
*
*
*
*
*
*
*
(
(
(
(
(
(
+
+
+
+
+
*
*
*
*
(
(
(
*
(
-
x
1
3
y
2
+
*
Кубенский А.А. Дискретная математика.
+
*
1
*
(
(
-
+
output
*
-
x
1
-
*
*

7.

Стек вместо рекурсии
Вместо рекурсивного вызова иногда имеет смысл сохранить контекст в стеке. Рассмотрим,
например, рекурсивный алгоритм быстрой сортировки.
public static void quickSort(int[] data, int from, int to) {
if (to-from > 1) {
int c = data[from];
// Выбираем некоторый элемент
// Распределяем элементы массива на значения меньшие и большие c.
int low = from, high = to;
while (low < high) {
while (low < high && data[--high] >= c) ; data[low] = data[high];
while (low < high && data[++low] <= c) ; data[high] = data[low];
}
data[low] = c;
// Независимо сортируем верхнюю и нижнюю половины массива
quickSort(data, from, low);
quickSort(data, low+1, to);
}
}
Вместо рекурсивного вызова будем записывать границы сортируемых участков в стек и
извлекать их по мере необходимости.
Кубенский А.А. Дискретная математика.

8.

Стек вместо рекурсии
private static class Pair {
int low, high;
Pair(int low, int high) { this.low = low; this.high = high; }
}
public static void quickSort(int[] data) {
Stack<Pair> stack = new StackImpl<>();
stack.push(new Pair(0, data.length));
while (!stack.isEmpty()) {
Pair pair = stack.pop();
int low = pair.low;
int high = pair.high;
int c = data[low];
// Выбираем некоторый элемент
while (low < high) {
while (low < high && data[--high] >= c) ; data[low] = data[high];
while (low < high && data[++low] <= c) ; data[high] = data[low];
}
data[low] = c;
if (low - pair.low > 1) stack.push(new Pair(pair.low, low));
if (pair.high - low > 2) stack.push(new Pair(low+1, pair.high));
}
}
Кубенский А.А. Дискретная математика.

9.

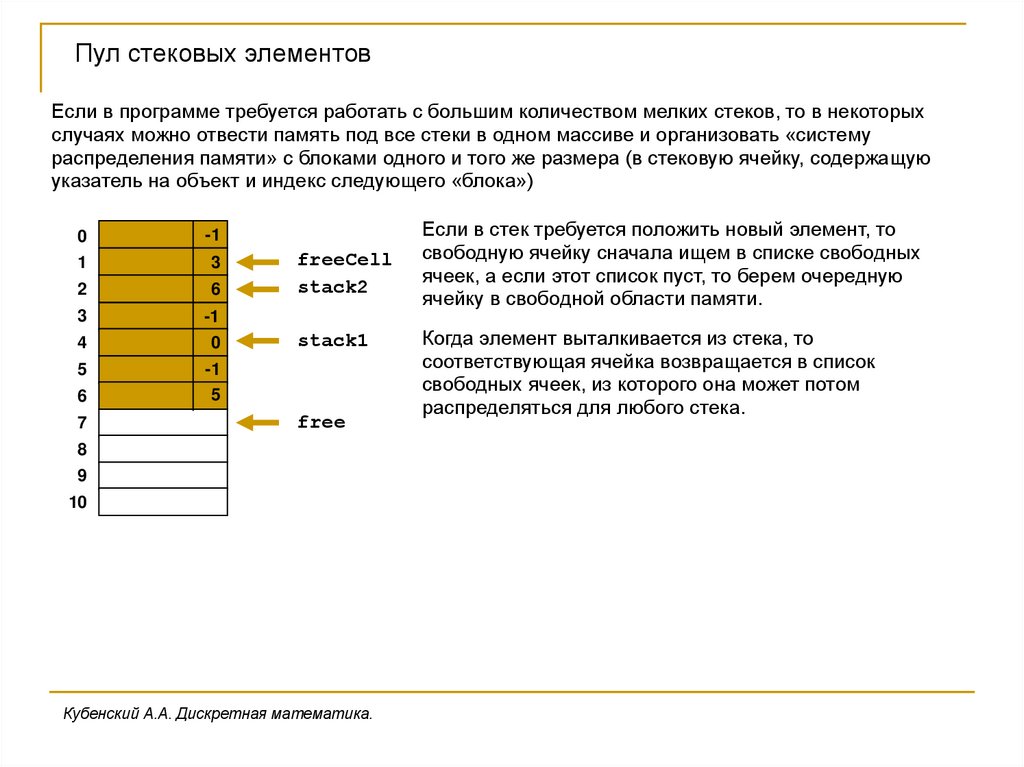
Пул стековых элементов
Если в программе требуется работать с большим количеством мелких стеков, то в некоторых
случаях можно отвести память под все стеки в одном массиве и организовать «систему
распределения памяти» с блоками одного и того же размера (в стековую ячейку, содержащую
указатель на объект и индекс следующего «блока»)
0
-1
1
3
2
6
3
-1
4
0
5
-1
5
6
7
freeCell
stack2
stack1
free
8
9
10
Кубенский А.А. Дискретная математика.
Если в стек требуется положить новый элемент, то
свободную ячейку сначала ищем в списке свободных
ячеек, а если этот список пуст, то берем очередную
ячейку в свободной области памяти.
Когда элемент выталкивается из стека, то
соответствующая ячейка возвращается в список
свободных ячеек, из которого она может потом
распределяться для любого стека.