Каркасы. Алгоритмизация и программирование. Язык С++, 11 класс

1.

1
Задача Штейнера
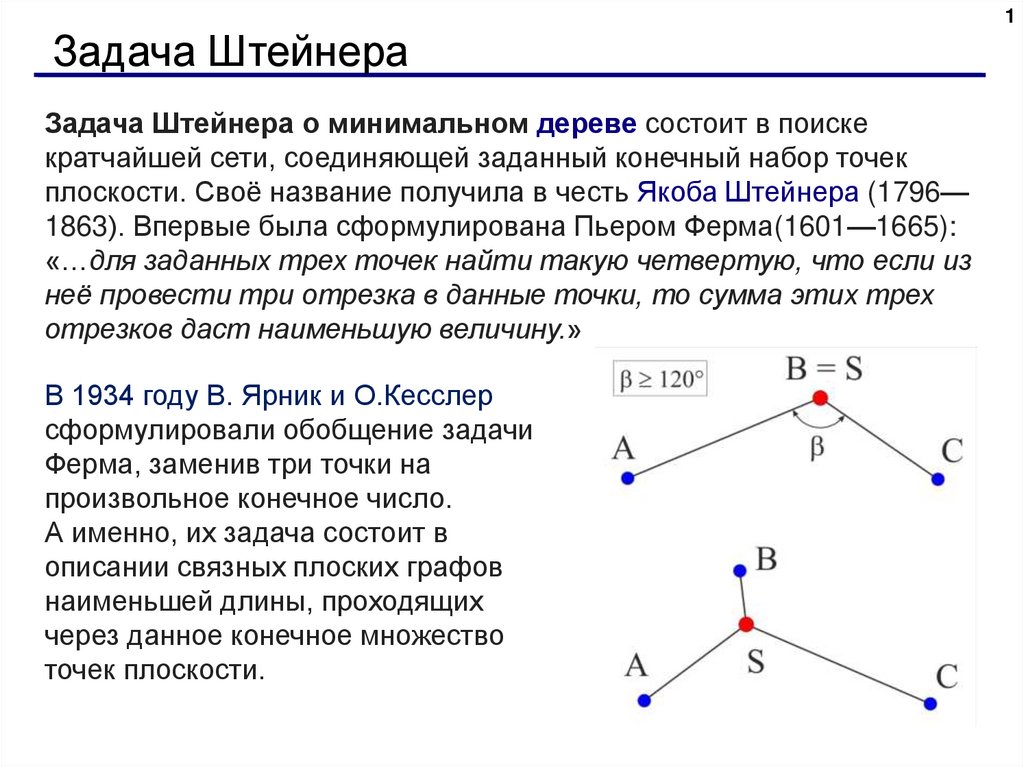
Задача Штейнера о минимальном дереве состоит в поиске
кратчайшей сети, соединяющей заданный конечный набор точек
плоскости. Своё название получила в честь Якоба Штейнера (1796—
1863). Впервые была сформулирована Пьером Ферма(1601—1665):
«…для заданных трех точек найти такую четвертую, что если из
неё провести три отрезка в данные точки, то сумма этих трех
отрезков даст наименьшую величину.»
В 1934 году В. Ярник и O.Кесслер
сформулировали обобщение задачи
Ферма, заменив три точки на
произвольное конечное число.
А именно, их задача состоит в
описании связных плоских графов
наименьшей длины, проходящих
через данное конечное множество
точек плоскости.

2.

2
Задача Прима-Краскала (Борувки-Ярника)
Задача: соединить N городов телефонной сетью так,
чтобы
длина
телефонных
линий
была
минимальная.
Та же задача: дан связный граф с N вершинами, веса
ребер заданы весовой матрицей W. Нужно найти
набор ребер, соединяющий все вершины графа
(остовное дерево) и имеющий наименьший вес.
7
0
3
2
1
8
4
5
3
6
4
0
1
2
3
4
0
0
7
3
5
∞
1
7
0
∞ 4
8
2
3
∞ 0 ∞ ∞
3
5
4
∞ 0
6
4
∞ 8 ∞ 6
0

3.

3
Жадный алгоритм
Жадный алгоритм – это многошаговый алгоритм, в котором на
каждом шаге принимается решение, лучшее в данный
момент.
В целом может получиться не оптимальное
! решение
(последовательность шагов)!
Шаг в задаче построения остовного дерева (каркаса) – это выбор
еще невыбранного ребра и добавление его к решению.
6
0
3
2
8
4
5
3
задаче построения каркаса
! Вжадный
алгоритм дает
1
7
4
оптимальное решение!

4.

4
Идея Отакара Борувки (1926) : Начиная с набора вершин
без рёбер (простейших компонент связности) добавлять
на каждом шаге минимальное из возможных рёбер,
соединяя две компоненты связности.
Идея Джозефа Краскала (1956) : Добавлять на каждом
шаге минимальное из возможных рёбер так, чтобы не
возникали циклы.
Идея Войцеха Ярника (1930) – Роберта Прима (1957) ,
Эдсгера Дейкстры (1959) : Сначала берётся
произвольная вершина и находится минимальное
инцидентное ей ребро. Затем, из рёбер, один конец
которых — уже принадлежит дереву, а другой — нет,
выбирается минимальное и присоединяется к дереву.
Рост дерева происходит до тех пор, пока не будут
исчерпаны все вершины исходного графа.

5.

5
Реализация алгоритма Краскала
Проблема: как проверить, что
1) ребро не выбрано, и
2) ребро не образует цикла с выбранными ребрами.
Решение: присвоить каждой вершине свой цвет и
перекрашивать вершины при добавлении ребра.
6
0
3
2
1
8
4
5
3
7
4
Алгоритм:
1) покрасить все вершины в разные цвета;
2) сделать N-1 раз в цикле:
выбрать ребро (i,j) минимальной длины из всех
ребер, соединяющих вершины разного цвета;
перекрасить все вершины, имеющие цвет j, в цвет i.
3) вывести найденные ребра.

6.

6
Реализация алгоритма Краскала
Структура «ребро»:
struct rebro {
int i, j;
// номера вершин
};
Основная программа:
весовая
цвета
const N = 5;
матрица
вершин
void main()
{
int W[N][N], Color[N], i, j,
k, min, col_i, col_j;
rebro Reb[N-1];
...
// здесь надо ввести матрицу W
for ( i = 0; i < N; i ++ ) // раскрасить вершины
Color[i] = i;
...
// основной алгоритм – заполнение массива Reb
...
// вывести найденные ребра (массив Reb)
}

7.

7
Реализация алгоритма Краскала
Основной алгоритм:
for ( k = 0; k < N-1; k ++ ) {
min = 30000; // большое число
нужно выбрать
N-1 ребро
цикл по всем
парам вершин
for ( i = 0; i < N-1; i ++ )
for ( j = i+1; j < N; j ++ )
if ( Color[i] != Color[j] &&
учитываем
только пары с
W[i][j] < min ) {
разным
min = W[i][j];
цветом вершин
Reb[k].i = i;
Reb[k].j = j;
запоминаем ребро и
col_i = Color[i];
цвета вершин
col_j = Color[j];
перекрашиваем
}
вершины цвета col_j
for ( i = 0; i < N; i ++ )
if ( Color[i] == col_j ) Color[i] = col_i;
}

8.

8
Сложность алгоритма
Основной цикл:
for ( k = 0; k < N-1; k ++ ) {
три вложенных
цикла, в каждом
число шагов <=N
...
for ( i = 0; i < N-1; i ++ )
for ( j = i+1; j < N; j ++ )
...
}
Количество операций:
O(N3) растет не быстрее, чем N3
Требуемая память:
int W[N][N], Color[N];
rebro Reb[N-1];
При предварительной
сортировке рёбер:
O(M log2M+N2)
O(N2)
По Приму с использованием множеств set - O((M+N) log2N)

9.

Алгоритмизация и программирование. Язык C++, 11 класс
9
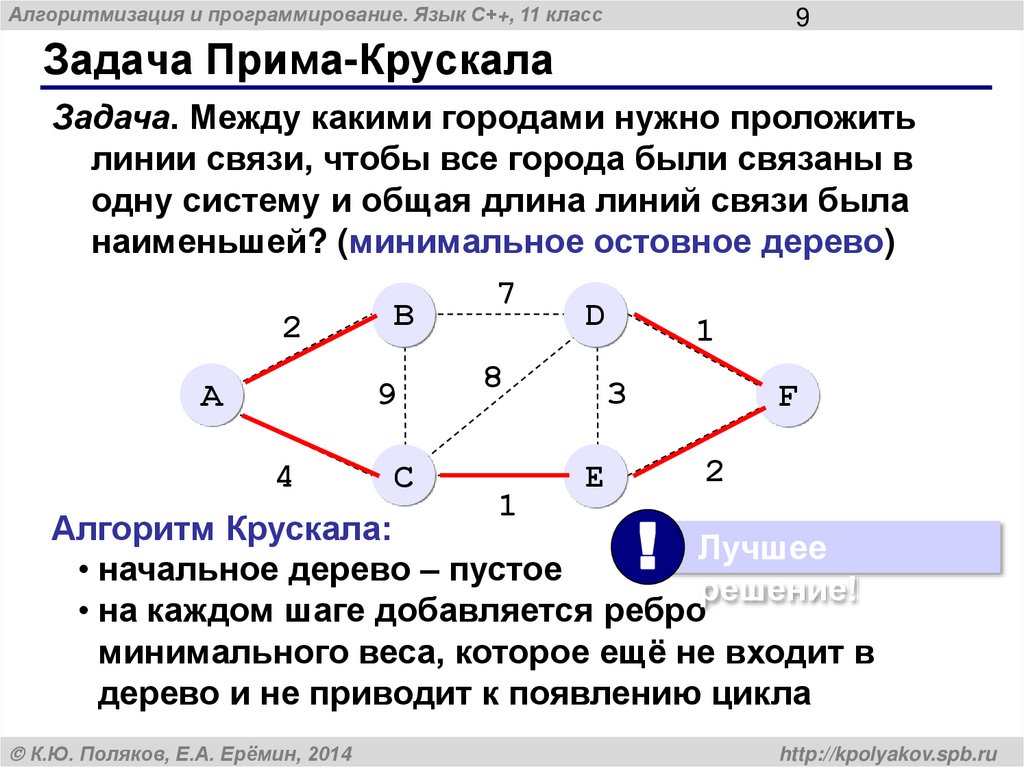
Задача Прима-Крускала
Задача. Между какими городами нужно проложить
линии связи, чтобы все города были связаны в
одну систему и общая длина линий связи была
наименьшей? (минимальное остовное дерево)
7
D
B
2
1
8
3
9
A
F
4
C
1
2
E
!
Алгоритм Крускала:
Лучшее
• начальное дерево – пустое
решение!
• на каждом шаге добавляется ребро
минимального веса, которое ещё не входит в
дерево и не приводит к появлению цикла
К.Ю. Поляков, Е.А. Ерёмин, 2014
http://kpolyakov.spb.ru

10.

Алгоритмизация и программирование. Язык C++, 11 класс
10
Раскраска вершин
2
B
9
A
4
C
7
D
8
1
1
3
E
for (i = 0; i < N; i ++) col[i] = i;
F
2
каждой
вершине
свой цвет
Сделать N-1 раз:
• ищем ребро минимальной длины среди всех
рёбер, концы которых окрашены в разные
цвета;
• найденное ребро (iMin,jMin) добавляется в
список выбранных, и все вершины, имеющие цвет
col[jMin], перекрашиваются в цвет col[iMin].
К.Ю. Поляков, Е.А. Ерёмин, 2014
http://kpolyakov.spb.ru

11.

Алгоритмизация и программирование. Язык C++, 11 класс
11
Раскраска вершин
Данные:
const int N = 6;
int W[N][N]; // весовая матрица
int col[N]; // цвета вершин
// номера вершин для выбранных ребер
int ostov[N-1][2];
int i, j, k, iMin, jMin, min, c;
Вывод результата:
for ( i = 0; i < N-1; i ++ )
cout << "(" << ostov[i][0] << ","
<< ostov[i][1] << ")" << endl;
К.Ю. Поляков, Е.А. Ерёмин, 2014
http://kpolyakov.spb.ru

12.

Алгоритмизация и программирование. Язык C++, 11 класс
12
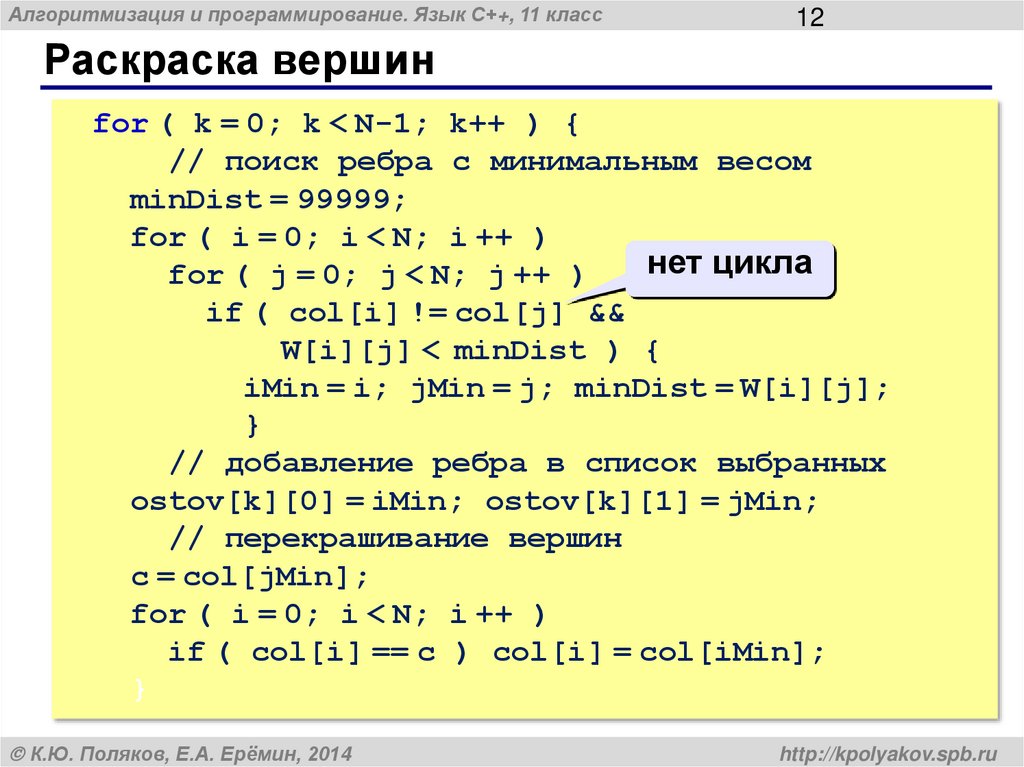
Раскраска вершин
for ( k = 0; k < N-1; k++ ) {
// поиск ребра с минимальным весом
minDist = 99999;
for ( i = 0; i < N; i ++ )
нет цикла
for ( j = 0; j < N; j ++ )
if ( col[i] != col[j] &&
W[i][j] < minDist ) {
iMin = i; jMin = j; minDist = W[i][j];
}
// добавление ребра в список выбранных
ostov[k][0] = iMin; ostov[k][1] = jMin;
// перекрашивание вершин
c = col[jMin];
for ( i = 0; i < N; i ++ )
if ( col[i] == c ) col[i] = col[iMin];
}
К.Ю. Поляков, Е.А. Ерёмин, 2014
http://kpolyakov.spb.ru