Базовые алгоритмы

1.

Базовые алгоритмы

2.

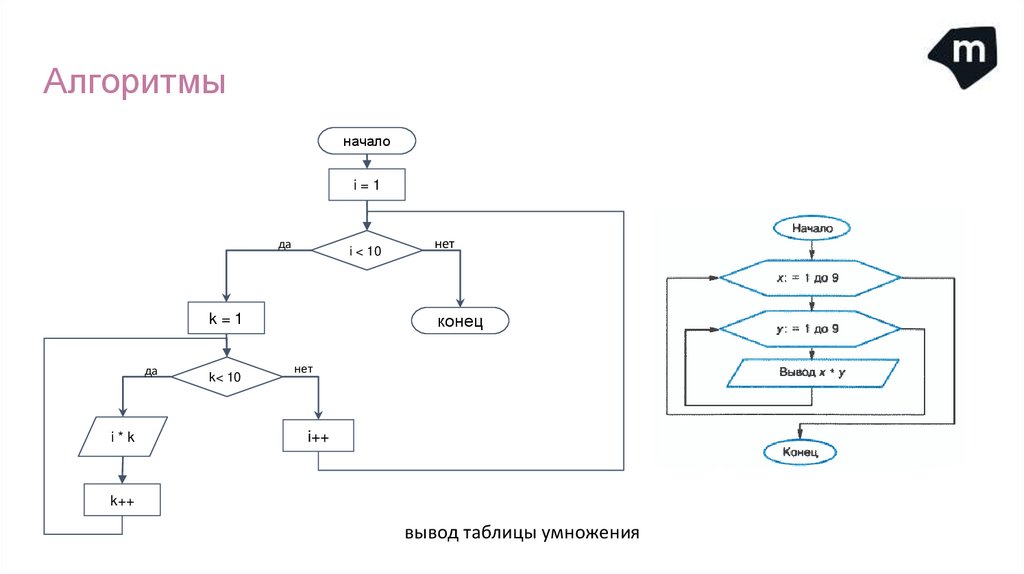
Алгоритмы
начало
i=1
да
i < 10
конец
k=1
да
i*k
k< 10
нет
нет
i++
k++
вывод таблицы умножения

3.

Алгоритмы
Все алгоритмы поиска делятся на
поиск в неупорядоченном множестве данных;
поиск в упорядоченном множестве данных.
Упорядоченность – наличие отсортированного ключевого поля.
Алгоритм последовательного поиска предполагает последовательный просмотр всех
записей множества, организованного как массив.

4.

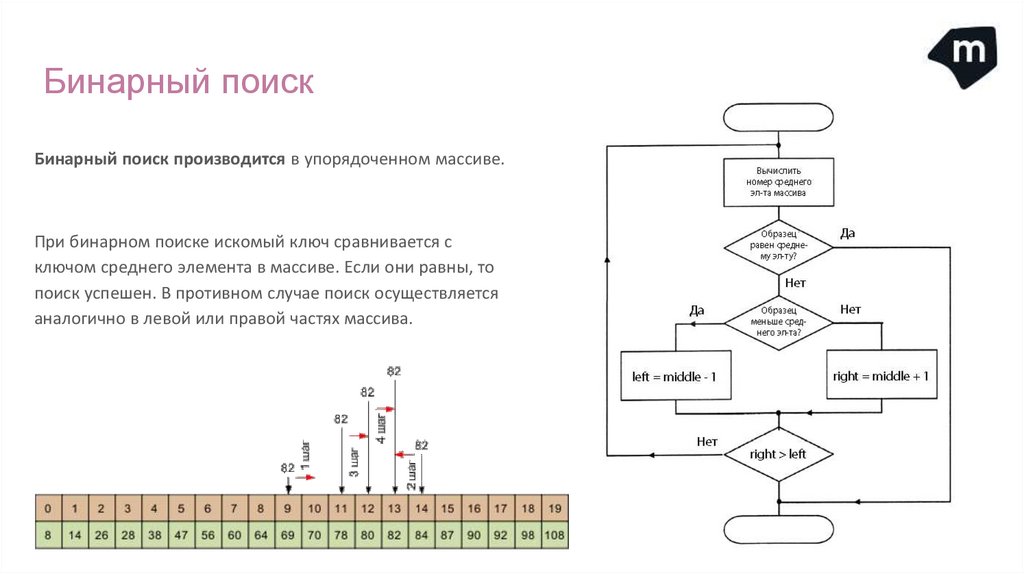
Бинарный поиск
Бинарный поиск производится в упорядоченном массиве.
При бинарном поиске искомый ключ сравнивается с
ключом среднего элемента в массиве. Если они равны, то
поиск успешен. В противном случае поиск осуществляется
аналогично в левой или правой частях массива.

5.

Алгоритмы сортировки
Сортировка — упорядочение (перестановка) элементов в подмножестве данных по какому-либо
критерию. Чаще всего в качестве критерия используется некоторое числовое поле, называемое
ключевым. Упорядочение элементов по ключевому полю предполагает, что ключевое поле каждого
следующего элемента не больше предыдущего (сортировка по убыванию). Если ключевое поле
каждого последующего элемента не меньше предыдущего, то говорят о сортировке по
возрастанию.
Все алгоритмы сортировки делятся на
● алгоритмы внутренней сортировки (сортировка массивов);
● алгоритмы внешней сортировки (сортировка файлов).

6.

Пузырьковая сортировка
Алгоритм пузырьковой сортировки предполагает сравнение соседних элементов.
В том случае, если их последовательность неверная, они меняются местами.
Сортировка осуществляется путем многократного прохождения по имеющемуся
массиву элементов
for (int i = 0; i < size - 1; i++)
{
for (int j = (size - 1); j > i; j--) // для всех элементов после
i-ого
{
if (num[j - 1] > num[j]) // если текущий элемент меньше
предыдущего
{
int temp = num[j - 1]; // меняем их местами
num[j - 1] = num[j];
num[j] = temp;
}
}
}

7.

Сортировка прямыми включениями
При сортировке вставкой массив проходится слева направо. Берём элемент (начиная с 1) и ищем, куда его можно
вставить в левой части массива так, чтобы слева находилось меньшее число, а справа — большее. И делаем так с
каждым последующим элементом.
Элементы входной последовательности просматриваются по одному, и каждый новый поступивший элемент
размещается в подходящее место среди ранее упорядоченных элементов
for (int i = 1; i < size; i++)
{
int value = num[i]; // запоминаем значение элемента
int index = i;
// и его индекс
while ((index > 0) && (num[index - 1] > value))
{
// смещаем другие элементы к концу массива пока они меньше index
num[index] = num[index - 1];
index--;
// смещаем просмотр к началу массива
}
num[index] = value; // рассматриваемый элемент помещаем на освободившееся место
}

8.

Сортировка шелла
Алгоритм сортировки, являющийся усовершенствованным вариантом сортировки вставками. Идея метода Шелла состоит в сравнении элементов,
стоящих не только рядом, но и на определённом расстоянии друг от друга. Иными словами — это сортировка вставками с предварительными
«грубыми» проходами.
Допустим, у нас есть массив элементов: (а1, а2, а3, а4, а5, а6, а7, а8, а9, а10, а11)
Применим алгоритм сортировки вставками к подмассиву, состоящему из каждого 5-го элемента, выглядеть он будет так: (а1, а6, а11)
Сохраняем результат сортировки в основном массиве. И теперь, с тем же интервалом между элементами, сдвигаемся на элемент вправо и сортируем
подмассив (а2, а7), затем то же самое для (а3, а8). И делаем так, пока не дойдём до конца массива.
Далее, возьмём подмассив из каждого 3-го элемента: (а1, а4, а7, а10)
Опять сохраняем результат сортировки в основном массиве. Затем, уже привычным движением сдвигаемся на один элемент вправо, получаем
подмассив: (а2, а5, а8, а11)
Сортируем так и далее.
for (int gap = length / 2; gap > 0; gap /= 2) { // 1st iteration gap is 8
for (int i = gap; i < length; i++) {
int key = array[i];
int j = i;
while (j >= gap && array[j - gap] > key) {
array[j] = array[j - gap];
j -= gap;
}
array[j] = key;
}
}

9.

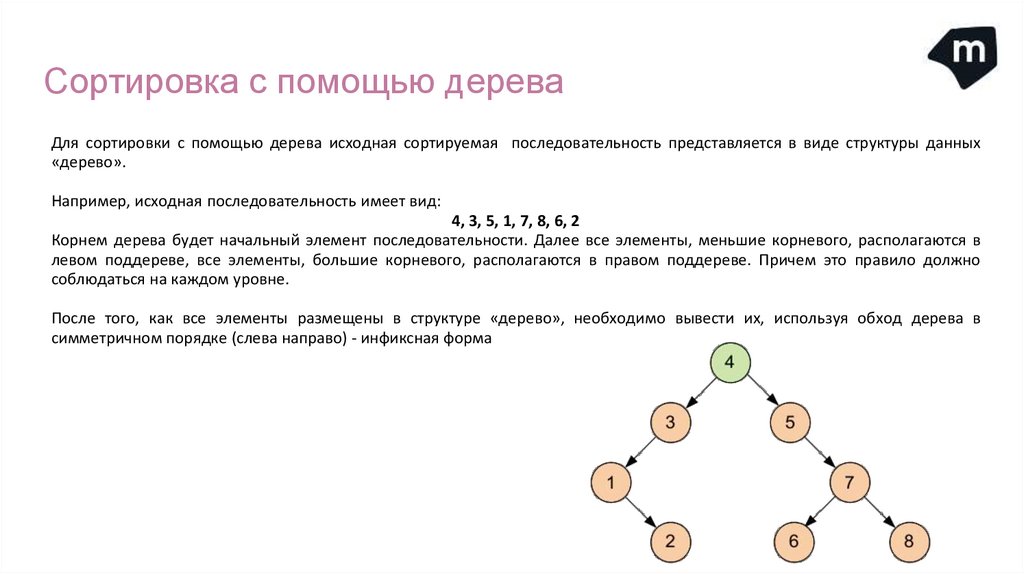
Сортировка с помощью дерева
Для сортировки с помощью дерева исходная сортируемая последовательность представляется в виде структуры данных
«дерево».
Например, исходная последовательность имеет вид:
4, 3, 5, 1, 7, 8, 6, 2
Корнем дерева будет начальный элемент последовательности. Далее все элементы, меньшие корневого, располагаются в
левом поддереве, все элементы, большие корневого, располагаются в правом поддереве. Причем это правило должно
соблюдаться на каждом уровне.
После того, как все элементы размещены в структуре «дерево», необходимо вывести их, используя обход дерева в
симметричном порядке (слева направо) - инфиксная форма