Похожие презентации:
Решение демонстрационного варианта
1.
2.
В одной из кодировок Unicode каждый символ кодируется 16 битами. Вова написал текст(в нём нет лишних пробелов):
«Ёж, лев, слон, олень, тюлень, носорог, крокодил, аллигатор — дикие животные».
Ученик вычеркнул из списка название одного из животных. Заодно он вычеркнул
ставшие лишними запятые и пробелы — два пробела не должны идти подряд.
При этом размер нового предложения в данной кодировке оказался на 16 байт меньше,
чем размер исходного предложения. Напишите в ответе вычеркнутое название животного.
Решение.
Поскольку один символ кодируется двумя байтами, из текста удалили 8 символов.
Заметим, что лишние запятая и пробел занимают четыре байта. Значит, название
животного, которое удалили из списка, должно состоять из шести букв, поскольку
(16 − 4) : 2 = 6 символов. Из всего списка только одно название животного состоит из 6
букв — тюлень.
Ответ: тюлень.
3.
Статья, набранная на компьютере, содержит 32 страницы, на каждойстранице 40 строк, в каждой строке 48 символов. Определите размер
статьи в кодировке КОИ -8, в которой каждый символ кодируется 8
битами.
Решение.
Найдем количество символов в статье:
32 · 40 · 48 = 25 · 5 · 23 · 3 · 24 = 15 · 212.
симв.
Один символ кодируется 8 бит, 210 байт составляют 1 Кбайт, поэтому информационный
объем статьи составляет
15 · 212 байт = 60 Кбайт. (15*212)/210=15*22
Ответ: 4.
4.
Валя шифрует русские слова (последовательности букв), записывая вместокаждой буквы её код:
А
01
Д
К
100 101
Н
10
О
С
111 000
Некоторые цепочки можно расшифровать не одним способом. Например, 00010101
может означать не только СКА, но и СНК. Даны три кодовые цепочки:
10111101
1010110
10111000
Найдите среди них ту, которая имеет только одну расшифровку, и запишите в
ответе расшифрованное слово.
5.
Решение.Проанализируем каждый вариант ответа:
1) «10111101» может означать как «КОА», так и «НОК».
2) «1010110» может означать как «КАН», так и «НКН».
3) «10111000» может означать только «НОС».
Следовательно, ответ «НОС».
6.
От разведчика была получена следующая шифрованная радиограмма, переданная сиспользованием азбуки Морзе:
•––•••–••––••–••–•––
При передаче радиограммы было потеряно разбиение на буквы, но известно, что в
радиограмме использовались только следующие буквы:
А
Д
Л
Т
Ж
•–
–•
•–•
–
•••–
Расшифруйте радиограмму. Запишите в ответе расшифрованную
радиограмму.
7.
Решение.Первые символы кода — «•–» — могут кодировать только букву А.
С символа «–» начинается только буква Д. Следующей буквой
может быть либо буква А, либо буква Л, однако, буква А нам не
подходит, поскольку в таком случае дальнейшая расшифровка
невозможна. Комбинация «–» соответствует букве Т, «–••» — букве
Д, «•–» — букве А.
Итак, шифром закодировано сообщение АДЛТДДТАТ.
8.
Между населёнными пунктами А, В, С, D, Е построены дороги, протяжённостькоторых (в километрах) приведена в таблице:
A
A
B
B
C
D
E
2
2
7
1
1
C
2
3
D
2
4
E
7
3
4
Определите длину кратчайшего пути между пунктами А и E.
Передвигаться можно только по дорогам, протяжённость которых
указана в таблице.
9.
Решение.Найдём все варианты маршрутов из A в E и выберем самый короткий.
Из
Из
Из
Из
пункта
пункта
пункта
пункта
A можно попасть в пункт B.
B можно попасть в пункты C, D, E.
C можно попасть в пункт E.
D можно попасть в пункт E.
A—B: длина маршрута 1 км.
A—B—C—E: длина маршрута 6 км.
A—B—D—E: длина маршрута 7 км.
A—B—E: длина маршрута 8 км.
Самый короткий путь: A—B—C—E. Длина маршрута 6 км.
Ответ: 6.
10.
У исполнителя Альфа две команды, которым присвоены номера:1. прибавь 1;
2. умножь на b
(b — неизвестное натуральное число; b ≥ 2).
Выполняя первую из них, Альфа увеличивает число на экране на 1, а выполняя вторую,
умножает это число на b. Программа для исполнителя Альфа — это последовательность
номеров команд. Известно, что программа 11211 переводит число 6 в число 82. Определите
значение b.
Решение.
Заметим, что после выполнения первых двух команд мы получаем число 8. Далее, составим и
решим уравнение:
8*b+2=82
8*b=80
b=10
2 способ, распишем команды по алгоритму:
((6+1)+1)=8, 8*b, ((8*b+1)+1)=82, 8b*2=82,
Ответ: 10.
b=10
11.
В программе «:=» обозначает оператор присваивания, знаки «+», «-», «*» и «/» —соответственно
операции сложения, вычитания, умножения и деления. Правила выполнения операций и
порядок действий
соответствуют правилам арифметики. Определите значение переменной b после выполнения
алгоритма:
а := 2
b := 4
а := 2*а + 3*b
b := a/2*b
ВРешение
ответе укажите одно целое число — значение переменной b.
а := 2
b := 4
а := 2*а + 3*b
2*2+3*4=16
b := a/2*b
16/2*4=32
В ответе укажите одно целое число — значение переменной b.
Ответ: 32
12.
У исполнителя Квадратор две команды, которым присвоены номера:1. прибавь 1
2. возведи в квадрат
Первая из них увеличивает число на экране на 1, вторая возводит его во вторую
степень.
Составьте алгоритм получения из числа 3 числа 84, содержащий не более 5
команд. В ответе запишите только номера команд.
(Например, 11221 — это алгоритм:
прибавь 1
прибавь 1
возведи в квадрат
возведи в квадрат
прибавь 1,
который преобразует число 1 в 82.)
Если таких алгоритмов более одного, то запишите любой из них.
13.
Решение.Не любое число является квадратом целого числа, поэтому, если мы пойдём от
числа 84 к числу 3, тогда однозначно восстановим программу. Полученные команды
будут записываться справа налево.
1. Число 84 не является квадратом, поэтому оно получено добавлением единицы к
числу 83: 84 = 83 + 1 (команда 1).
2. Число 83 не является квадратом, поэтому оно получено добавлением единицы к
числу 82: 83 = 82 + 1 (команда 1).
3. Число 82 не является квадратом, поэтому оно получено добавлением единицы к
числу 81: 82 = 81 + 1 (команда 1).
4. Число 81 является квадратом числа 9: 81 = 9 · 9 (команда 2).
5. Число 9 является квадратом числа 3: 9 = 3 · 3 (команда 2).
Искомая последовательность команд: 22111.
Ответ: 22111.
14.
Файл размером 64 Кбайт передаётся через некоторое соединение со скоростью 1024бит в секунду.
Определите размер файла (в Кбайт), который можно передать за то же время через
другое соединение со скоростью 256 бит в секунду. В ответе укажите одно число —
размер файла в Кбайт. Единицы измерения писать не нужно
Решение:
U1= 1024 бит/сек
V1= 64 Кб
t1=t2
U2=256 бит/сек
V2=?
V=U*t t=V/U
64/1024=x/256 x= (64*256)/1024=16
Ответ: 16
15.
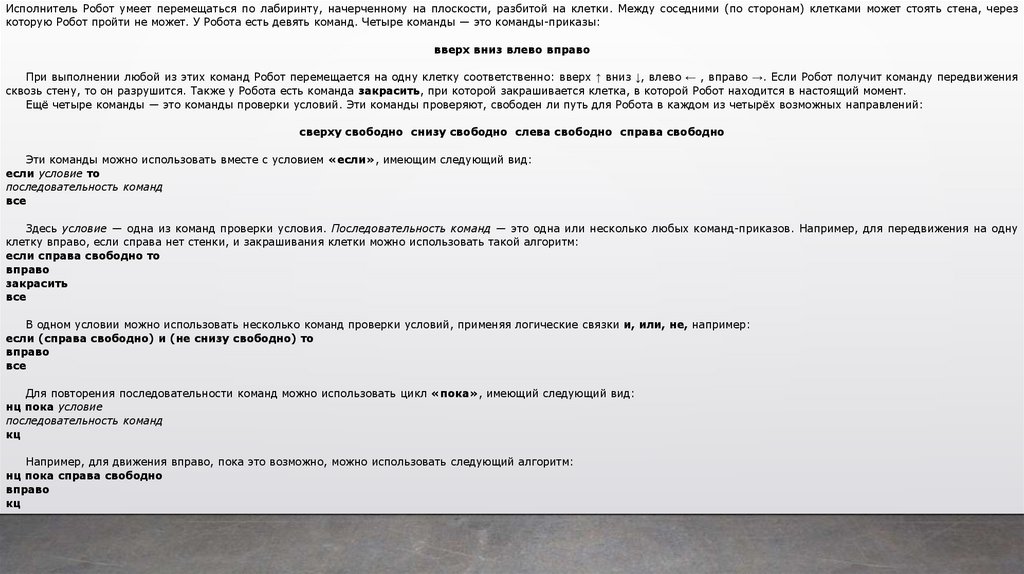
Исполнитель Робот умеет перемещаться по лабиринту, начерченному на плоскости, разбитой на клетки. Между соседними (по сторонам) клетками может стоять стена, черезкоторую Робот пройти не может. У Робота есть девять команд. Четыре команды — это команды-приказы:
вверх вниз влево вправо
При выполнении любой из этих команд Робот перемещается на одну клетку соответственно: вверх ↑ вниз ↓, влево ← , вправо →. Если Робот получит команду передвижения
сквозь стену, то он разрушится. Также у Робота есть команда закрасить, при которой закрашивается клетка, в которой Робот находится в настоящий момент.
Ещё четыре команды — это команды проверки условий. Эти команды проверяют, свободен ли путь для Робота в каждом из четырёх возможных направлений:
сверху свободно снизу свободно слева свободно справа свободно
Эти команды можно использовать вместе с условием «если», имеющим следующий вид:
если условие то
последовательность команд
все
Здесь условие — одна из команд проверки условия. Последовательность команд — это одна или несколько любых команд-приказов. Например, для передвижения на одну
клетку вправо, если справа нет стенки, и закрашивания клетки можно использовать такой алгоритм:
если справа свободно то
вправо
закрасить
все
В одном условии можно использовать несколько команд проверки условий, применяя логические связки и, или, не, например:
если (справа свободно) и (не снизу свободно) то
вправо
все
Для повторения последовательности команд можно использовать цикл «пока», имеющий следующий вид:
нц пока условие
последовательность команд
кц
Например, для движения вправо, пока это возможно, можно использовать следующий алгоритм:
нц пока справа свободно
вправо
кц
16.
Выполните задание.На бесконечном поле есть горизонтальная и вертикальная
стены. Правый конец горизонтальной стены соединён с
верхним концом вертикальной стены. Длины стен неизвестны.
В каждой стене есть ровно один проход, точное место прохода
и его ширина неизвестны. Робот находится в клетке,
расположенной непосредственно под горизонтальной стеной у
её левого конца. На рисунке указан один из возможных
способов расположения стен и Робота (Робот обозначен
буквой «Р»).
Напишите для Робота алгоритм, закрашивающий все
клетки,
расположенные
непосредственно
ниже
горизонтальной стены и левее вертикальной стены. Проходы
должны остаться незакрашенными. Робот должен закрасить
только
клетки,
удовлетворяющие
данному
условию.
Например, для приведённого выше рисунка Робот должен
закрасить следующие клетки (см. рисунок).
При исполнении алгоритма Робот не должен разрушиться,
выполнение алгоритма должно завершиться. Конечное
расположение Робота может быть произвольным. Алгоритм
должен решать задачу для любого допустимого расположения
стен и любого расположения и размера проходов внутри стен.
Алгоритм может быть выполнен в среде формального
исполнителя или записан в текстовом редакторе. Сохраните
алгоритм в текстовом файле.
17.
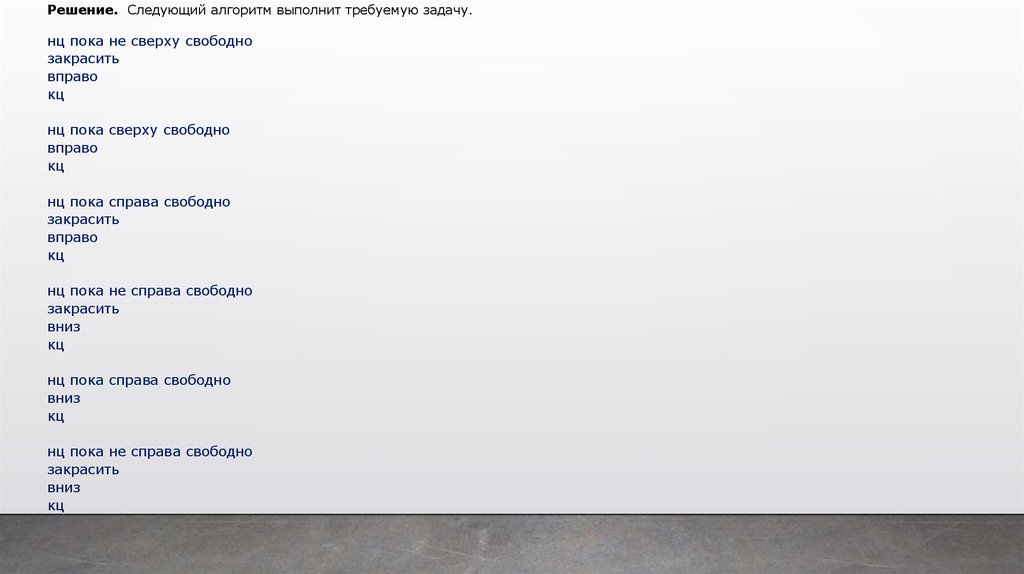
Решение. Следующий алгоритм выполнит требуемую задачу.нц пока не сверху свободно
закрасить
вправо
кц
нц пока сверху свободно
вправо
кц
нц пока справа свободно
закрасить
вправо
кц
нц пока не справа свободно
закрасить
вниз
кц
нц пока справа свободно
вниз
кц
нц пока не справа свободно
закрасить
вниз
кц
















 Информатика
Информатика








