Теория вероятности и её применение

1.

ГБОУ РО «БККК»
Теория вероятности.
Тема :« Теория вероятности и её применение»
Выполнил:
кадет взвода 9/2
Митрохин Станислав Олегович
Проверил:
преподаватель теории вероятности
Бочарова Ольга Петровна
11.02 2023

2.

3.

4.

5.

6.

7.

Вероятность того, что на тесте по биологии учащийся О. верно решит больше 11 задач, равна 0,67.
Вероятность того, что О. верно решит больше 10 задач, равна 0,74. Найдите вероятность того, что О.
верно решит ровно 11 задач.
Решение.
Рассмотрим события A = «учащийся решит 11 задач» и В = «учащийся решит больше 11 задач». Их
сумма — событие A + B = «учащийся решит больше 10 задач». События A и В несовместные,
вероятность их суммы равна сумме вероятностей этих событий: P(A + B) = P(A) + P(B). Тогда,
используя данные задачи, получаем: 0,74 = P(A) + 0,67, откуда P(A) = 0,74 − 0,67 = 0,07. Ответ: 0,07.
Вероятность того, что на тесте по химии учащийся П. верно решит больше 8 задач, равна 0,48.
Вероятность того, что П. верно решит больше 7 задач, равна 0,54. Найдите вероятность того, что П.
верно решит ровно 8 задач.
Решение.
Вероятность решить несколько задач складывается из суммы вероятностей решить каждую из этих
задач. Больше 8: решить 9-ю, 10-ю ... Больше 7: решить 8-ю, 9-ю, 10-ю ...Вероятность решить 8-ю =
0,54-0,48=0,06. Ответ:0.06

8.

9.

Если гроссмейстер А. играет белыми, то он выигрывает у гроссмейстера Б. с вероятностью 0,52. Если А.
играет черными, то А. выигрывает у Б. с вероятностью 0,3. Гроссмейстеры А. и Б. играют две партии,
причем во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.
Решение
Решение. Возможность выиграть первую и вторую партию не зависят друг от друга. Вероятность
произведения независимых событий равна произведению их вероятностей: 0,52 · 0,3 = 0,156. Ответ: 0,156.
Помещение освещается фонарём с двумя лампами. Вероятность перегорания лампы в течение года
равна 0,3. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
Решение
Найдем вероятность того, что перегорят обе лампы. Эти события независимые, вероятность их
произведения равно произведению вероятностей этих событий: 0,3·0,3 = 0,09.
Событие, состоящее в том, что не перегорит хотя бы одна лампа, противоположное. Следовательно, его
вероятность равна 1 − 0,09 = 0,91

10.

11.

Физика.
Во второй половине 19 века была в работах Максвелла, Больцмана и Гиббса была развита
статистическая механика, которая описывала состояние разряженных систем, содержащих огромное
число частиц (порядка числа Авогадро). Если раньше понятие распределения случайной величины было
преимущественно связано с распределением ошибок измерения, то теперь распределенными оказались
самые разные величины – скорости, энергии, длины свободного пробега.
Сельское хозяйство.
В начале 20 века в Англии была поставлена задача количественного сравнения эффективности
различных методов ведения сельского хозяйства. Для решения этой задачи была развита теория
планирования экспериментов, дисперсионный анализ. Основная заслуга в развитии этого уже чисто
практического использования статистики принадлежит сэру Рональду Фишеру, астроному(!) по
образованию, а в дальнейшем фермеру, статистику, генетику, президенту английского Королевского
общества. Современная математическая статистика, пригодная для широкого применения в практике,
была развита в Англии (Карл Пирсон, Стьюдент, Фишер). Стьюдент впервые решил задачу оценки
неизвестного параметра распределения без использования байесовского подхода.
Промышленность.
Введение методов статистического контроля на производстве (контрольные карты Шухарта). Сокращение
необходимого количества испытаний качества продукции. Математические методы оказываются уже
настолько важными, что их стали засекречивать. Так книга с описанием новой методики, позволявшей
сократить количество испытаний (“Последовательный анализ” Вальда), была издана только после
окончания второй мировой войны в 1947 году.

12.

Примеров использования вероятности в реальной жизни
Прогнозирование погоды
Возможно, наиболее распространенным примером использования вероятности в реальной жизни
является прогнозирование погоды.
Вероятность используется синоптиками для оценки вероятности того, что в определенный день в
определенной области будет дождь, снег, облака и т. Д.
Синоптики регулярно говорят что-то вроде “вероятность дождя сегодня составляет 80% между 14:00 и
17:00”, чтобы указать, что вероятность дождя в определенные часы высока.
Стихийные бедствия
Экологические департаменты стран часто используют вероятность для определения вероятности
стихийного бедствия, такого как ураган, торнадо, землетрясение и т. Д. ударит по стране в данном году.
Если вероятность достаточно высока, то департамент будет принимать решения о жилье, распределении
ресурсов и т. Д., Которые сведут к минимуму последствия стихийного бедствия.
Трафик
Обычные люди используют вероятность каждый день, когда решают куда-нибудь поехать.
На основе времени суток, местоположения в городе, погодных условий и т. Д. мы все склонны делать
вероятностные прогнозы о том, насколько плохим будет трафик в течение определенного времени.

13.

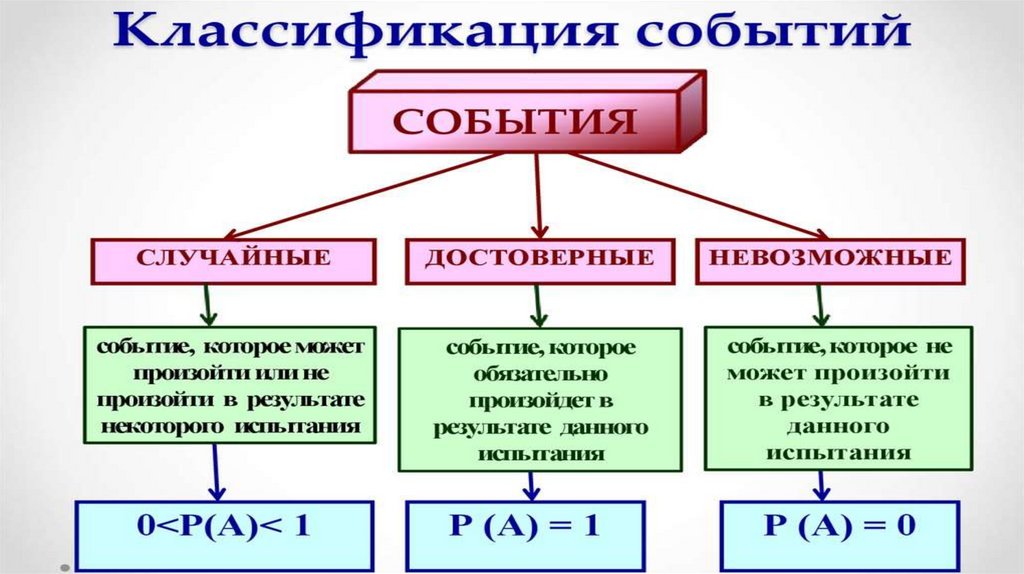
вывод
Мы познакомились с определением теории вероятностей. Изучили историю
возникновения. Узнали, что теория вероятностей изучает закономерности,
возникающие в случайных экспериментах. Случайным называют
эксперимент, результат которого нельзя предсказать заранее.
Невозможность предсказать результат отличает случайное явление от
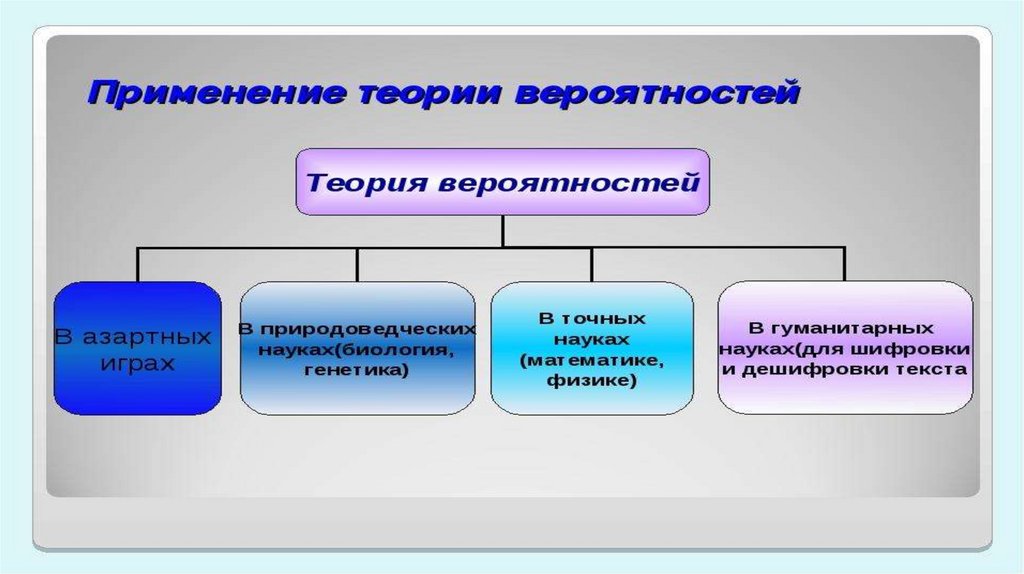
определяемого. Практическое применение теории вероятностей велико.
Человек часто применяет теорию вероятностей в повседневном быту, хотя
может и не знать математические формулы. С помощью формул и примеров
научились решать задачи на определение классической вероятности.
Таким образом, рассмотрев теорию вероятности, ее положения и
возможности, можно утверждать, что возникновение данной теории не было
случайным явлением в науке, а было вызвано необходимостью дальнейшего
развития технологии