Опыт моделирования сейсмических данных 2D в Seismic Unix

1.

KSM #49
Опыт моделирования сейсмических данных 2D в Seismic Unix:
от технических нюансов к моделированию сейсмических данных
Тестирование алгоритмов ослабления поверхностной волны на
модельных данных 2D с различным шагом по ПП
Применение некоторых процедур временной обработки к
модельным сейсмическим данным 2D
ООО «ПетроТрейс»
Москва 2022

2.

Опыт моделирования сейсмических данных 2D в Seismic Unix:
от технических нюансов к моделированию сейсмических данных
2

3.

Вводная информация
Seismic Unix (SU) – это открытый пакет программ для обработки сейсмических данных без интерфейса.
Взаимодействие с программами можно осуществлять через командную строку или с помощью скриптов.
Основы работы в SU и общая концепция хорошо описаны в первых трех главах (Introduction, Unix Commands
and Concepts, Trace Headers and Windowing Data) книги Seismic Data Processing with Seismic Unix (David Forel, Thomas
Benz, and Wayne D. Pennington). Рекомендуется к прочтению. После прочтения многие вопросы сразу отпадут.
Из того, что может быть полезным сейчас:
- если ввести название программы из SU (без аргументов) в командную строку и нажать Enter, появится
документация к этой программе (для программы fdelmodc необходимо при этом находиться на c7mmos1);
- можно посмотреть демонстрации выполнения множества программ из SU. Найти их можно здесь:
/apps/other/cwp/src/demos. В папке demos есть множество файлов README, перед запуском скриптов желательно
эти файлы прочитать. Также, вероятно, лучше запускать скрипты не напрямую из папки demos, чтобы случайно не
перезаписать/удалить/изменить что-то нужное.
- в целом, расширения у выходных файлов могут быть любые. Но среди пользователей SU есть некие
соглашения по поводу расширений файлов. Полезно их знать, потому что они используются в демонстрационных
скриптах и вообще в литературе. Стоит их придерживаться, потому что это облегчает коммуникацию по теме SU.
Сейчас важны следующие расширения файлов:
*.su – бинарные сейсмические данные (которые в отличие от segy-файлов не содержат текстовый заголовок
edcdic и бинарный заголовок, а содержат только трассы с заголовками трасс);
*.dat – бинарные несейсмические данные.
3

4.

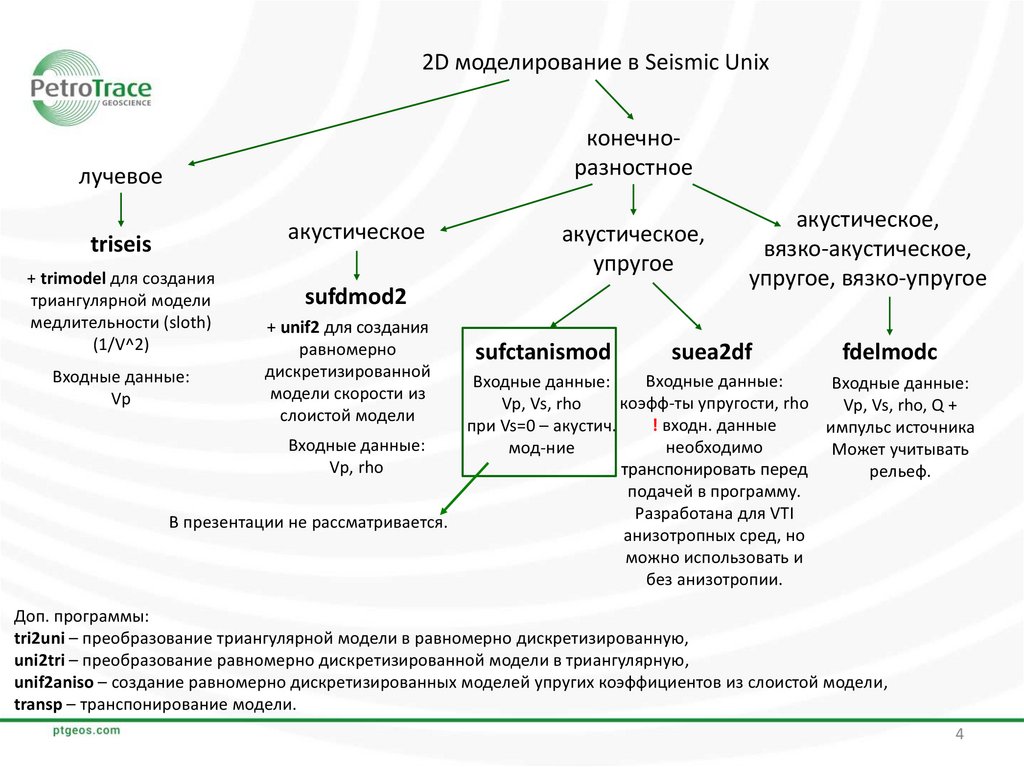
2D моделирование в Seismic Unix
конечноразностное
лучевое
акустическое
triseis
+ trimodel для создания
триангулярной модели
медлительности (sloth)
(1/V^2)
Входные данные:
Vp
акустическое,
упругое
sufdmod2
+ unif2 для создания
равномерно
дискретизированной
модели скорости из
слоистой модели
Входные данные:
Vp, rho
В презентации не рассматривается.
sufctanismod
акустическое,
вязко-акустическое,
упругое, вязко-упругое
suea2df
fdelmodc
Входные данные:
Входные данные:
Входные данные:
коэфф-ты упругости, rho
Vp, Vs, rho
Vp, Vs, rho, Q +
! входн. данные
при Vs=0 – акустич.
импульс источника
необходимо
мод-ние
Может учитывать
транспонировать перед
рельеф.
подачей в программу.
Разработана для VTI
анизотропных сред, но
можно использовать и
без анизотропии.
Доп. программы:
tri2uni – преобразование триангулярной модели в равномерно дискретизированную,
uni2tri – преобразование равномерно дискретизированной модели в триангулярную,
unif2aniso – создание равномерно дискретизированных моделей упругих коэффициентов из слоистой модели,
transp – транспонирование модели.
4

5.

Программа triseis (лучевое моделирование)
Входные данные: триангулярная модель медлительности (sloth, 1/V^2), которую можно создать с помощью
программы trimodel или преобразовать из равномерно дискретизированной модели с помощью программы
uni2tri (также всегда есть вариант загрузить из segy-файла, но после этого модель все равно нужно преобразовать
в триангулярную с помощью uni2tri).
В программе trimodel модель среды задается, по сути, вручную. Отдельно задаются границы, затем слои
между границами заливаются значением медлительности. Можно задавать градиенты медлительности. В целом, с
помощью этой программы сложную модель задать проблематично. Главное, что эта программа создает
триангулярную модель, подходящую для программы лучевого моделирования triseis.
Также можно создать модель в программе unif2. С помощью этой программы создаются равномерно
дискретизированные модели (по сути, матрицы значений). В целом, как и triseis, unif2 – «ручная» программа. В
отличие от triseis в unif2 границы модели задаются из внешнего текстового файла. Эта программа подходит для
создания моделей типа ГСС или с наклонными слоями.
Для использования полученной с помощью unif2 модели в программе моделирования triseis необходимо
преобразовать модель из равномерно дискретизированной в триангулярную. Сделать это можно с помощью
программы uni2tri (также есть обратная программа tri2uni).
Перед моделированием сейсмограмм можно выполнить трассирование лучей и посмотреть, как будут
выглядеть лучи (волновое поле) для конкретной модели (программа psmerge). Также с помощью программы
psmerge можно подобрать параметры лучевого моделирования, которые затем можно будет указать в программе
triseis.
Программа triseis за одно выполнение моделирует одну трассу с импульсом, соответствующим одной границе
модели. Поэтому для получения сейсмограммы, «зарегистрированной» более чем одним приемником с
отражениями от всех границ модели, необходимо использовать циклы (цикл по границам модели и цикл по
приемникам). Для моделирования набора сейсмограмм необходимо также добавить цикл по источникам.
5

6.

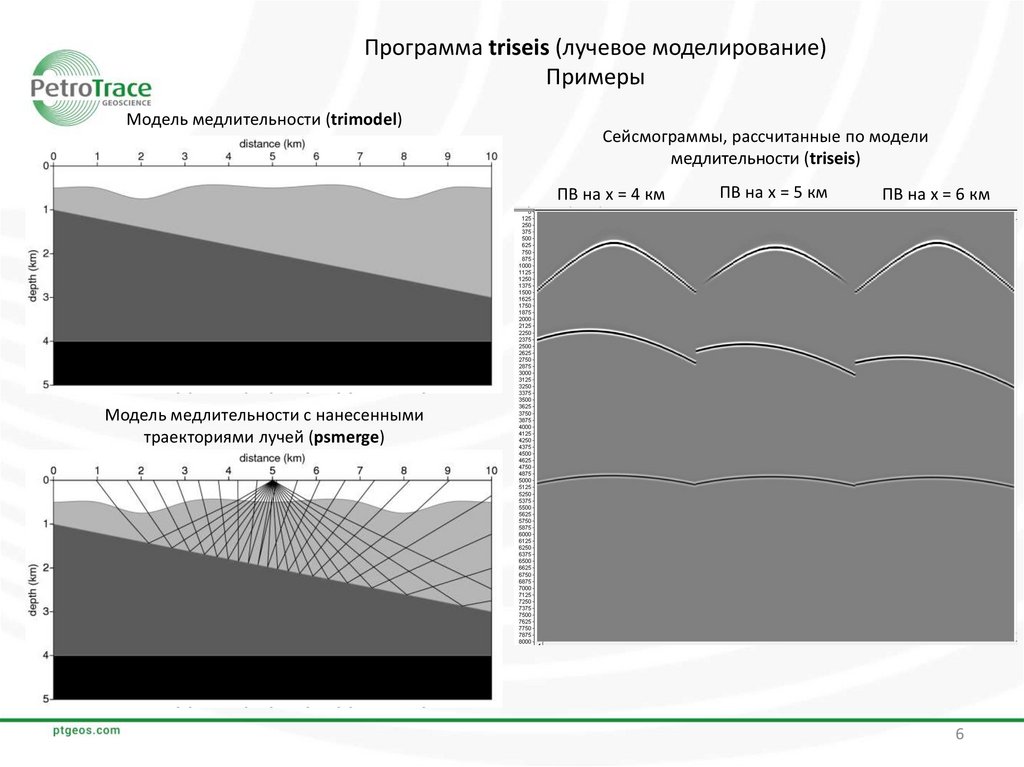
Программа triseis (лучевое моделирование)
Примеры
Модель медлительности (trimodel)
Сейсмограммы, рассчитанные по модели
медлительности (triseis)
ПВ на х = 4 км
ПВ на х = 5 км
ПВ на х = 6 км
Модель медлительности с нанесенными
траекториями лучей (psmerge)
6

7.

Программа sufdmod2 (акустическое моделирование)
Входные данные: глубинная скоростная модель, плотностная модель (опционально). Исходные модели
можно создать с помощью программы unif2 или других средств SU, можно загрузить из segy-файла.
Программа автоматически рассчитывает временной шаг дискретизации dt по формуле: dt = dz/2Vmax, где
Vmax – максимальная скорость в скоростной модели, dz – шаг дискретизации скоростной модели по глубине.
Получаемые на выходе программы модельные сейсмограммы будут иметь шаг дискретизации dt.
Количество отсчетов в трассах получаемых сейсмограмм рассчитывается по формуле: nt = 1 + tmax/dt, где
tmax – по сути, длина записи в секундах, задается пользователем.
Программа обязательно должна выписывать волновое поле, иначе возникнет ошибка: segy output can’t be tty.
Можно выписывать поле в файл-пустышку /dev/null.
Бинарный файл скоростей (и плотностей), с которым работает программа, представляет собой матрицу без
каких-либо заголовков.
Программа не понимает отрицательные глубины.
При некорректном задании пространственного и временного шагов дискретизации в полученных данных
может наблюдаться численная дисперсия. Для схем 2 порядка (как в программе sufdmod2) на длину волны
должны приходиться 10-11 узлов сетки, для схем 4 порядка – примерно 5 узлов.
При этом соотношение пространственной и временной разрешающих способностей должно быть
ограничено. В программе sufdmod2 для ограничения используется следующее условие (Courant-Friedrichs-Levy):
Vmax*dt/dx<=Cmax, где Vmax – максимальная скорость в модели, dx – шаг по сетке (если по осям x и z шаги
отличны, то меньший из них); Cmax изменяется в зависимости от метода, используемого для решения дискретного
уравнения.
Заглубление приемников не может быть равно 0 или 1 м. Заглубление источника может быть равно 0 м (то
есть источник может располагаться на дневной поверхности).
Плотность задается в г/см3 (но можно задавать и в кг/м3, поскольку в вычислениях размерность сокращается;
итоговый результат не зависит от размерности плотности).
fmax – максимальная частота источника: fmax = Vmin/10h, Vmin – минимальная скорость в модели, h – шаг по
вертикали (dz). fpeak = favg = fmax/2.
7

8.

Программа suea2df (акустическое и упругое моделирование)
Входные данные: разрезы коэффициентов упругости (можно создать с помощью программы unif2aniso,
можно пересчитать из разрезов скоростей продольных и поперечных волн, предварительно загруженных из segyфайла или созданных программой unif2 или других средств SU), плотностная модель (опционально).
! Перед подачей моделей на вход программы suea2df модели необходимо транспонировать (transp).
При работе в режиме упругого моделирования без анизотропии достаточно задать два упругих коэффициента
c11 и c55, которые рассчитываются по формулам:
Для акустического моделирования без анизотропии необходим только файл с11. Однако для программы оба
файла с11 и с55 являются обязательными, поэтому нужно будет также подать на вход файл с55, заполненный
нулями.
Для анизотропного случая (для VTI среды) упругие коэффициенты рассчитываются через параметры Томсена
по следующим формулам:
Диапазоны изменений
параметров Томсена
(взято из help к программе unif2aniso):
! с11 для изотропного и анизотропного случаев отличаются.
Шаг дискретизации dt задается пользователем.
Согласно help ячейки исходных моделей должны быть квадратными (dx = dz).
Есть возможность выгрузить модельный импульс источника в текстовый файл.
8

9.

Программа fdelmodc
(акустическое, вязко-акустическое, упругое, вязко-упругое моделирование)
Входные данные: Vp, Vs, rho, Q + импульс источника.
Программа была разработана для моделирования измерений сейсмической интерферометрии (шумные
сигналы источников, расположенных случайно; большие длины записи).
Основное отличие от других конечно-разностных алгоритмов заключается в возможности использовать
частотно-ограниченные шумные сигнатуры источников, расположенных случайно в приповерхностном слое, и
моделировать общий эффект от всех этих источников только на одном шаге моделирования.
Шаги дискретизации по x и z в исходных моделях должны быть одинаковыми.
Если необходимо задать область модели, в которой волны не распространяются, нужно задать скорости в этой
области равными нулю. Плотность нулевой задавать не нужно, иначе будет ошибка.
Граничные условия. Есть возможность задавать ширину зоны тейперинга (параметр ntaper, количество узлов
сетки). По умолчанию: ntaper = 4cpmax/(fmax*dx), то есть 4 длины волны. cpmax – максимальная скорость
продольных волн в модели, fmax – максимальная частота источника, dx – размер ячейки модели. В зависимости от
размера ячейки ширины зоны тейперинга в 40-80 ячеек может быть достаточно. Чем больше зона, тем сильнее
поглощение и дольше выполняется моделирование. Все границы, для которых «включен» тейперинг, используют
одну и ту же ширину зоны. Разные задавать нельзя.
Помещение источника P на свободную поверхность (z = 0) приведет к тому, что никакая энергия не проникнет
в среду, и итоговые файлы будут содержать только 0 (это связано с граничными условиями). Волны от Fz источника
(src_type = 7), расположенного на поверхности z = 0, проникают в среду. Этот источник является альтернативой
источника P.
Помещение источника P на один узел ниже свободной поверхности симулирует дипольный источник.
Отрицательная часть диполя – отражение от свободной поверхности. Помещение приемников на один узел ниже
свободной поверхности также приводит к дипольному отклику.
Приемники Vz на свободной поверхности измеряют волновое поле, P-приемники ничего не измеряют.
От свободной поверхности всегда будет приходить отражение. Для ослабления спутника от источника можно
использовать программу baseop option=ghost (примитивная).
9

10.

Программа fdelmodc
(акустическое, вязко-акустическое, упругое, вязко-упругое моделирование)
Рельеф
Программа может учитывать рельеф. Для этого скорости должны быть равны 0 выше рельефа. Для
помещения источника или приемника на рельеф достаточно поместить его (источник или приемник) в корректную
латеральную позицию выше рельефа. В программе осуществляется поиск по глубине до 1-ого ненулевого
значения скорости и в это место помещается источник или приемник.
Параметр sinkdepth = n помещает пункт приема на n узлов сетки ниже обнаруженного 1-ого ненулевого
значения на линии рельефа. Параметр sinkdepth_src = n помещает пункт возбуждения на n узлов сетки ниже
обнаруженного 1-ого ненулевого значения на линии рельефа.
В заголовках d2 и d1 данных, подаваемых на вход программы, должна храниться информация о шагах
дискретизации по горизонтали и вертикали (они должны быть равны друг другу). Заголовок d2 соответствует dx,
заголовок d1 – dz. Заносить значения в заголовки можно с помощью программы sushw. Если в заголовках данных
dx = dz = 0, то нужно прописать значение шага дискретизации в скрипте. Если dx = dx = n, n > 0, то значение n
автоматически считается программой из заголовков данных.
Можно задавать шаг по пунктам приема, отличный от сетки моделей параметров.
Перед началом вычислений программа проверяет, выполняются ли условия стабильности и отсутствия
дисперсии. Если условия не выполняются, скрипт выдает ошибку с предложением, как нужно изменить шаг
дискретизации или максимальную частоту сигнала, чтобы получить стабильную схему. Эту проверку можно
обойти, задав значение параметра fmax в соответствии с предложенным программой. Эти критерии (стабильности
и дисперсии) не работают для вязко-упругих сред.
10

11.

Моделирование сейсмических данных 2D
(конечно-разностное, упругое, программа fdelmodc)
11

12.

Параметры моделирования
Для моделирования 2D сейсмограмм использовалась программа fdelmodc, входящая в состав
пакета утилит Seismic Unix. В программе реализованы 4 конечно-разностные схемы, позволяющие
осуществить акустическое, вязко-акустическое, упругое и вязко-упругое 2D моделирование волновых
полей.
В рамках данного эксперимента выполнялось только акустическое и упругое моделирование.
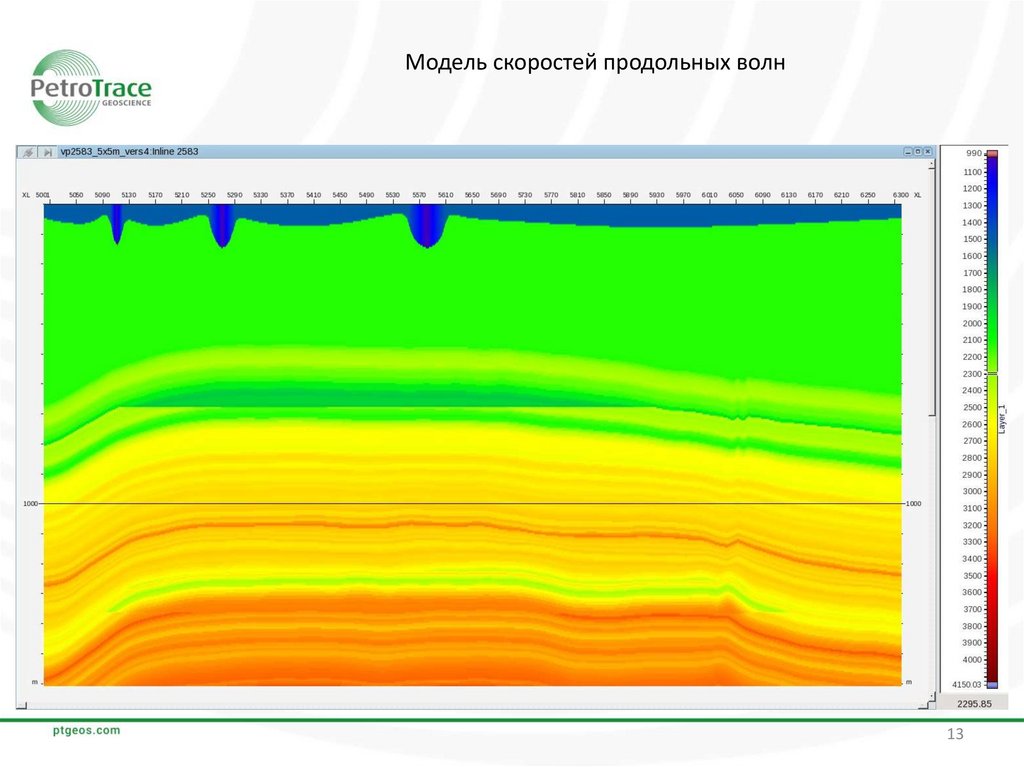
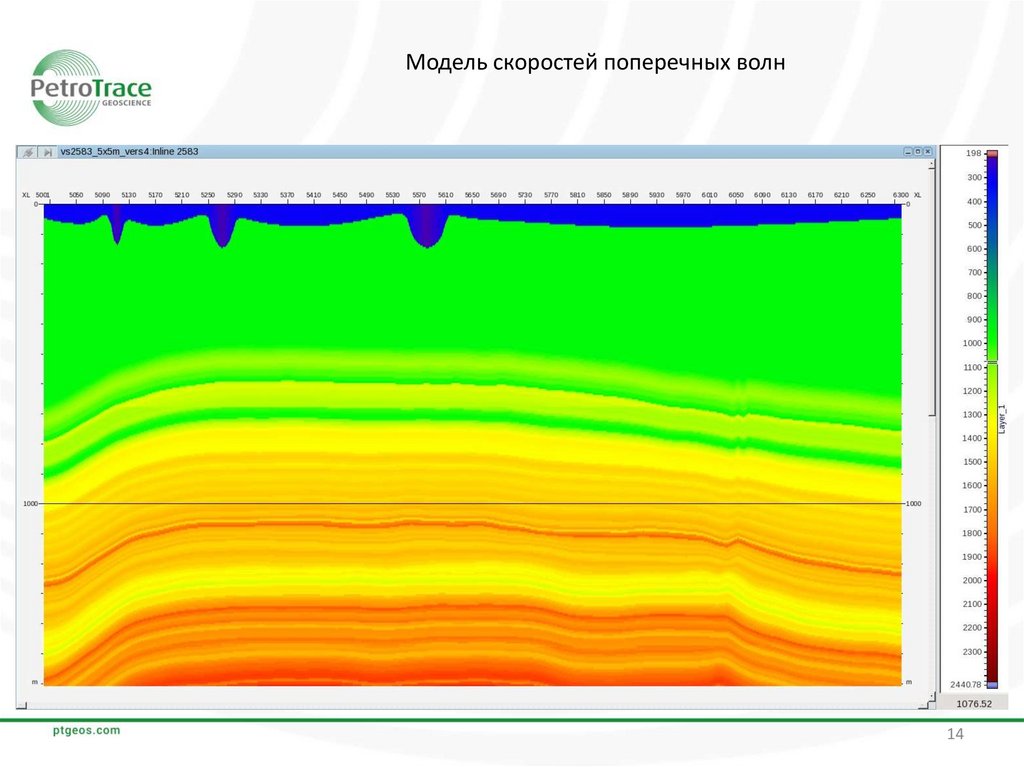
Входными данными программы fdelmodc являются разрезы скоростей продольных и
поперечных волн, разрез плотностей и файл с импульсом источника. Импульс источника был
сгенерирован в одной из программ моделирования Seismic Unix и выгружен в текстовый файл.
Импульс источника в данном эксперименте – производная гауссиана, средняя частота 30 Гц,
длительность 50 мс.
Параметры моделирования:
- размер ячейки исходных моделей: 5х5 м;
- шаг дискретизации по времени (используется в процессе моделирования): 0.5 мс;
- граничные условия: дневная поверхность – свободная граница; левая, правая и нижняя
границы модели – поглощающие границы с зоной тейперинга 100 узлов;
- источники и приемники заглублены на 10 м относительно дневной поверхности;
- шаг по ПВ 50 м, шаг по ПП 5 м;
Источник
- длина записи 4 с, шаг дискретизации выходных данных 2 мс.
t, мс
12

13.

Модель скоростей продольных волн
13

14.

Модель скоростей поперечных волн
14

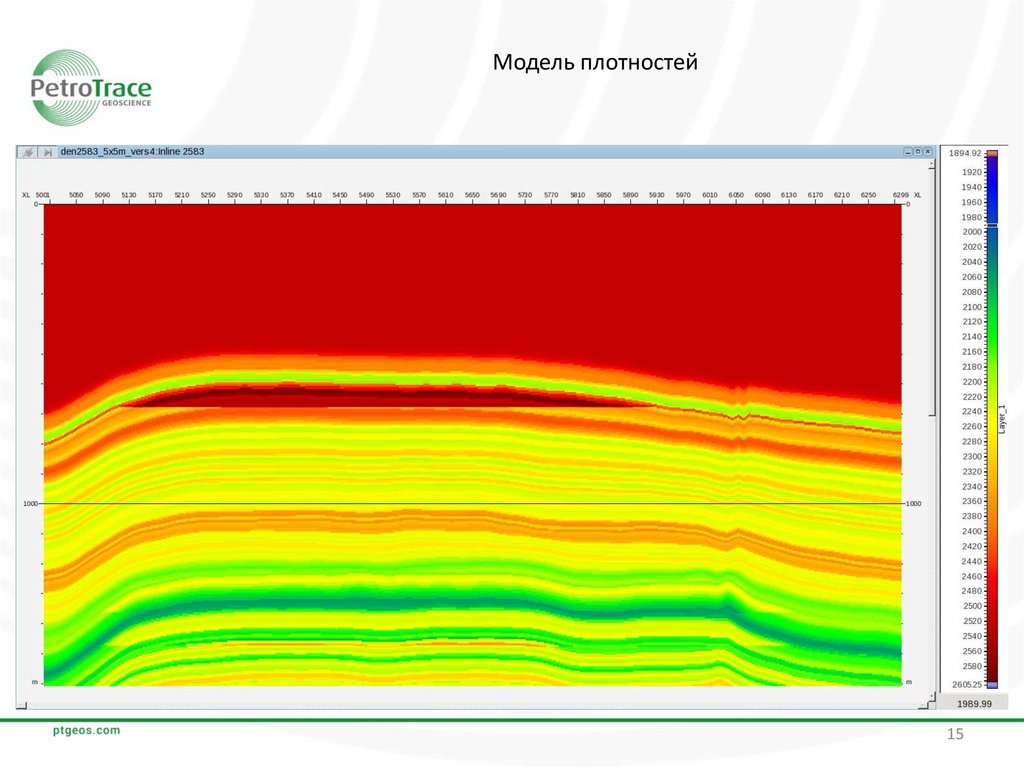
15.

Модель плотностей
15

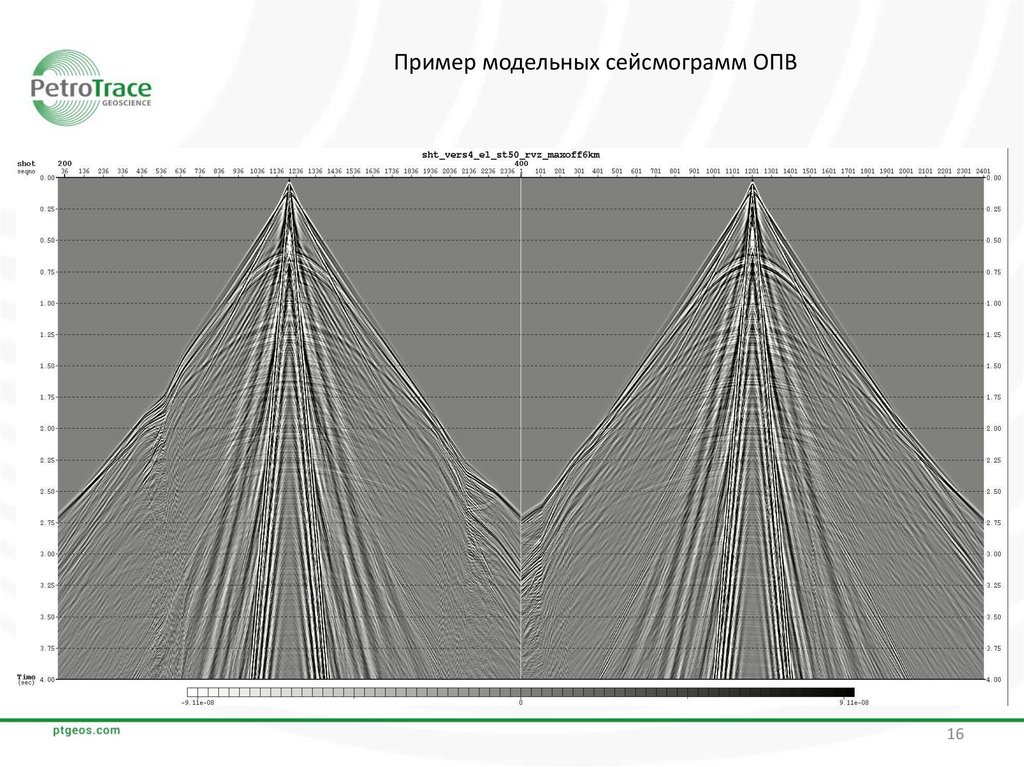
16.

Пример модельных сейсмограмм ОПВ
16

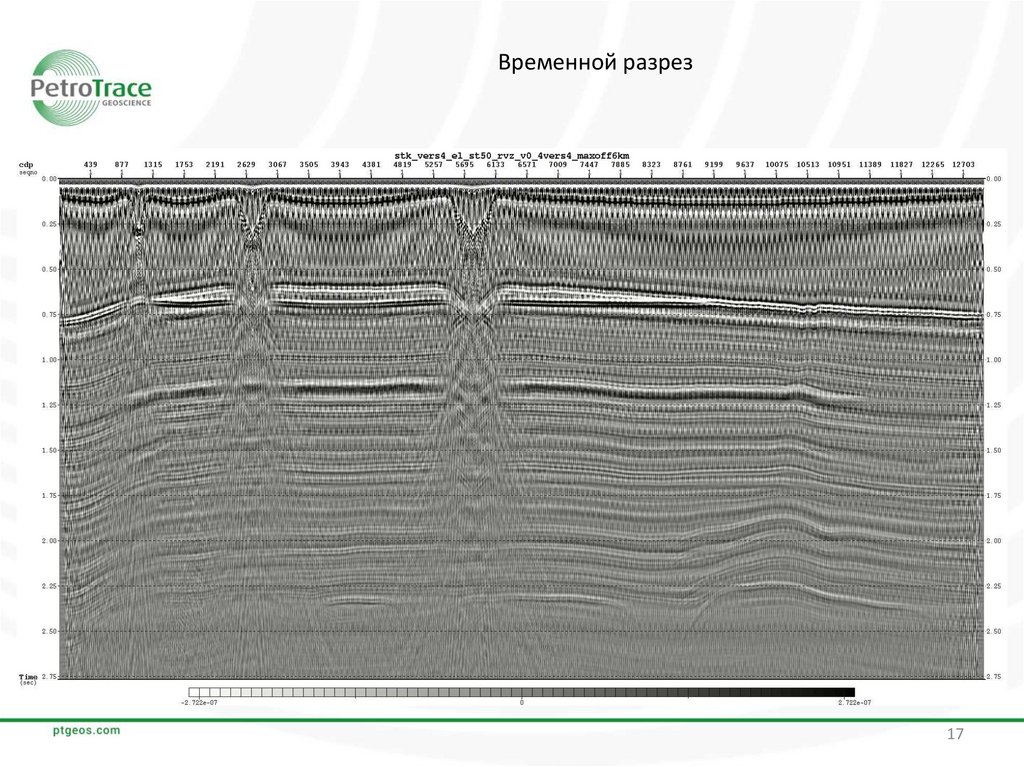
17.

Временной разрез
17

18.

Тестирование алгоритмов ослабления поверхностной волны на
модельных данных 2D с различным шагом по ПП
18

19.

Введение
Цель данного этапа – тестирование алгоритмов ослабления поверхностных волн на модельных
сейсмограммах с различными интервалами между пунктами приема (ПП).
В начале работ из исходного набора модельных сейсмических данных с шагом между ПП 5 м были
получены наборы с интервалами между ПП 15, 25, 50 и 100 м.
Для ослабления поверхностных волн на всех имеющихся наборах данных использовались два
алгоритма – низкочастотная фильтрация массива (LFAF) и F-K фильтрация (FKFILT).
LFAF осуществляет ослабление линейных помех по следующему алгоритму:
1. Преобразование сейсмограмм из области t-x в область f-x;
2. Свертка каждой частотной компоненты из заданного частотного диапазона (диапазона, в
котором требуется ослабить линейные волны-помехи) с прямоугольной функцией определенной
длины;
3. Обратное преобразование сейсмограмм из области f-x в область t-x.
При F-K фильтрации сейсмограммы преобразуются из области t-x в область f-k (частота – волновое
число). В области f-k происходит разделение различных типов волн, и за счет этого появляется
возможность их локализации и подавления. Таким образом, при F-K фильтрации основной задачей
является построение фильтра по F-K изображению или, иначе говоря, задание области на F-K
изображении, внутри которой требуется выполнить подавление. Построение фильтра можно
выполнять путем задания полигонов или наклонов.
19

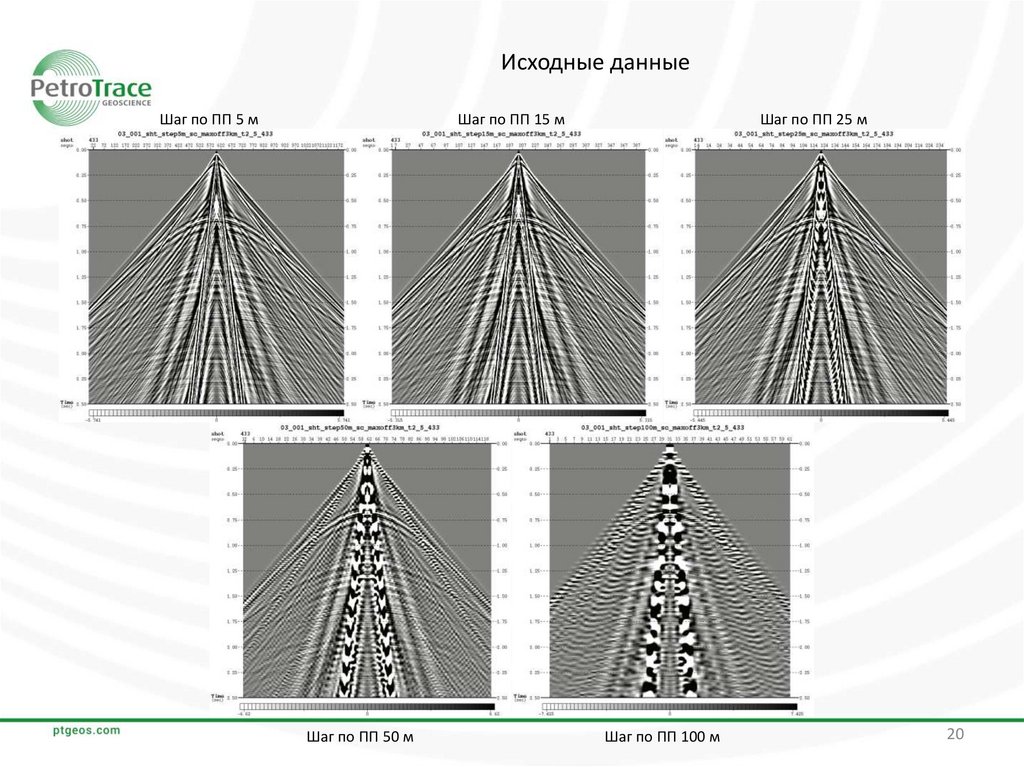
20.

Исходные данные
Шаг по ПП 5 м
Шаг по ПП 25 м
Шаг по ПП 15 м
Шаг по ПП 50 м
Шаг по ПП 100 м
20

21.

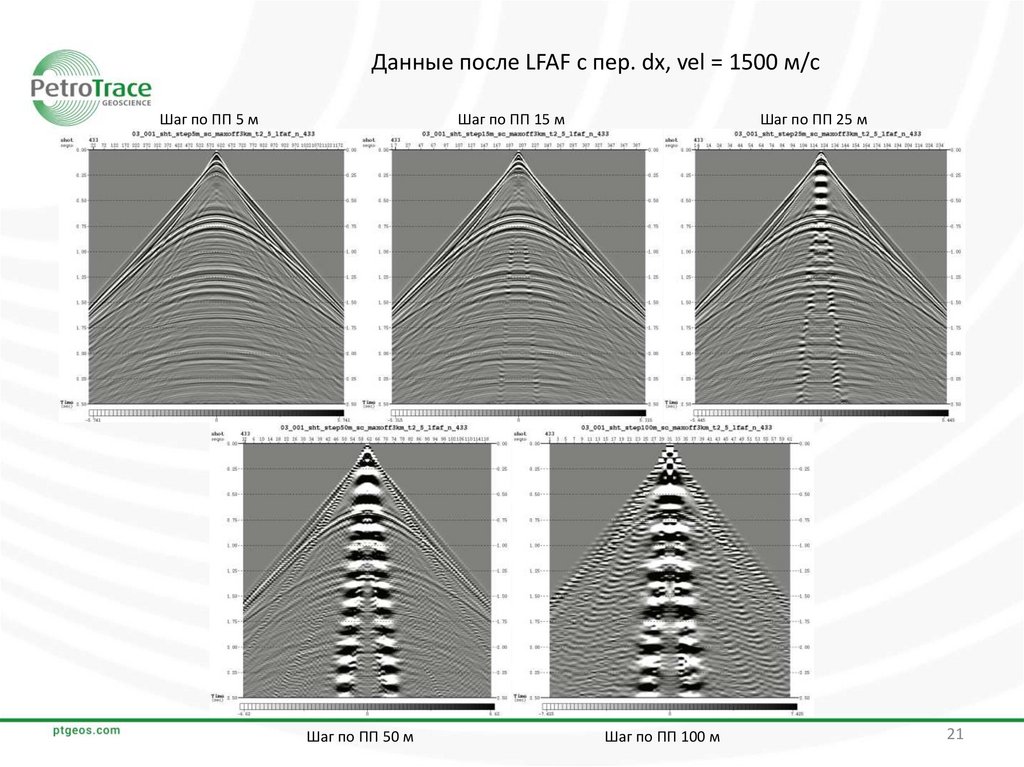
Данные после LFAF с пер. dx, vel = 1500 м/с
Шаг по ПП 5 м
Шаг по ПП 25 м
Шаг по ПП 15 м
Шаг по ПП 50 м
Шаг по ПП 100 м
21

22.

Разность между исходными данными и данными после LFAF
с пер. dx, vel = 1500 м/с
Шаг по ПП 5 м
Шаг по ПП 25 м
Шаг по ПП 15 м
Шаг по ПП 50 м
Шаг по ПП 100 м
22

23.

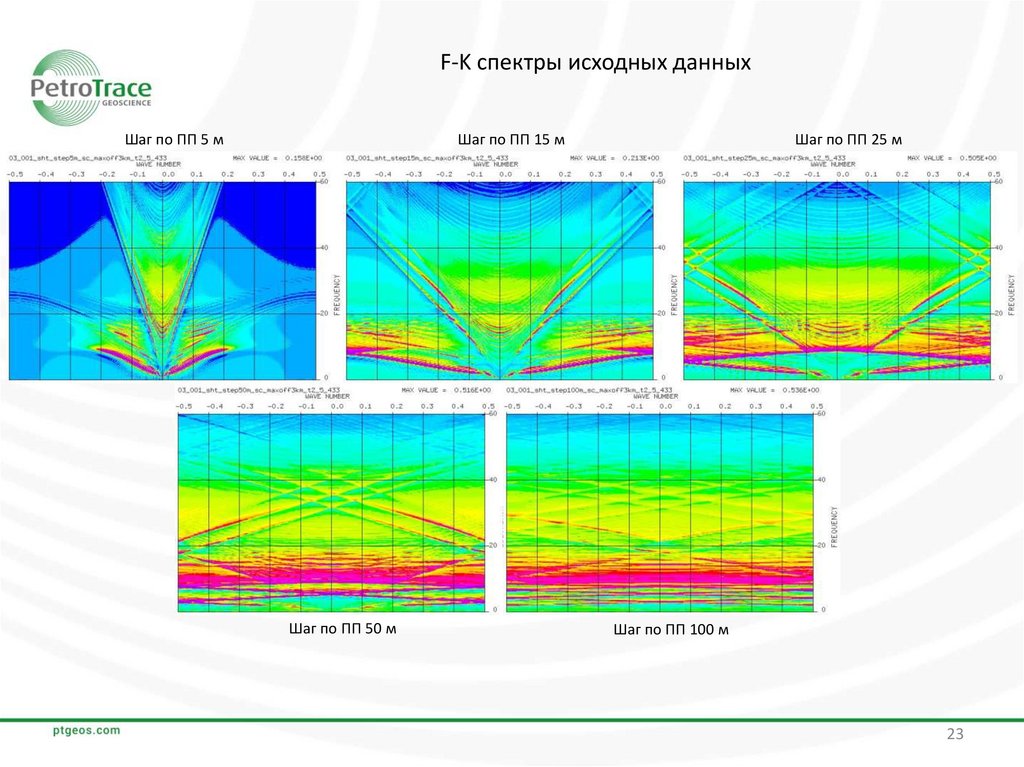
F-K спектры исходных данных
Шаг по ПП 5 м
Шаг по ПП 15 м
Шаг по ПП 50 м
Шаг по ПП 25 м
Шаг по ПП 100 м
23

24.

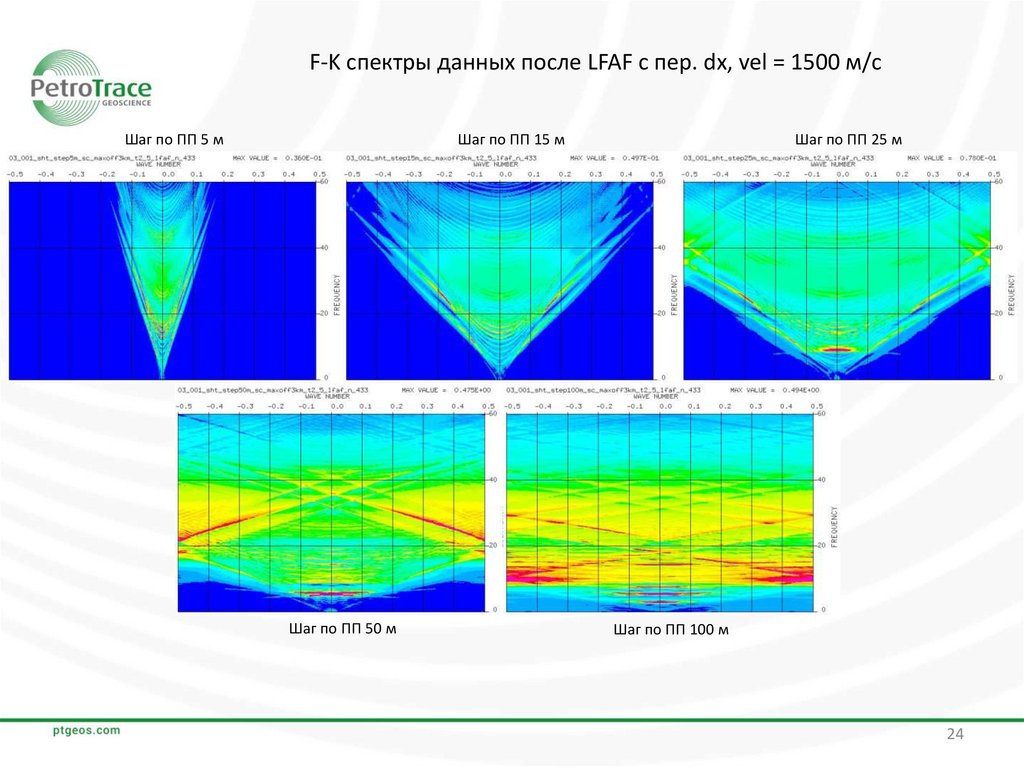
F-K спектры данных после LFAF с пер. dx, vel = 1500 м/с
Шаг по ПП 5 м
Шаг по ПП 15 м
Шаг по ПП 50 м
Шаг по ПП 25 м
Шаг по ПП 100 м
24

25.

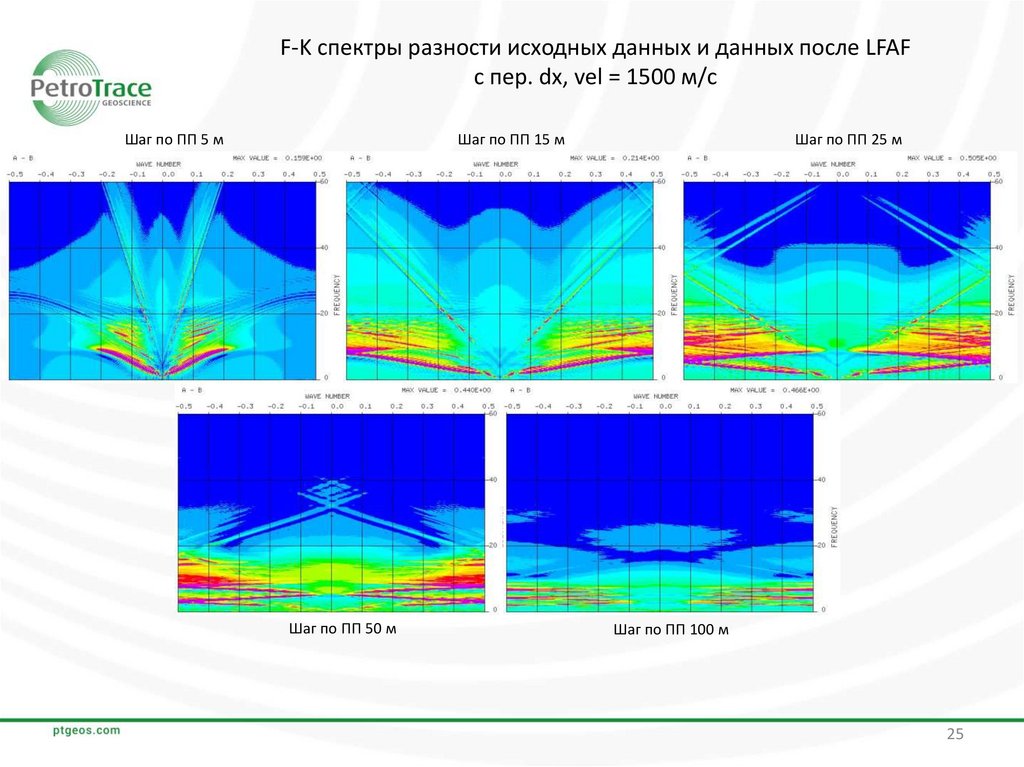
F-K спектры разности исходных данных и данных после LFAF
с пер. dx, vel = 1500 м/с
Шаг по ПП 5 м
Шаг по ПП 15 м
Шаг по ПП 50 м
Шаг по ПП 25 м
Шаг по ПП 100 м
25

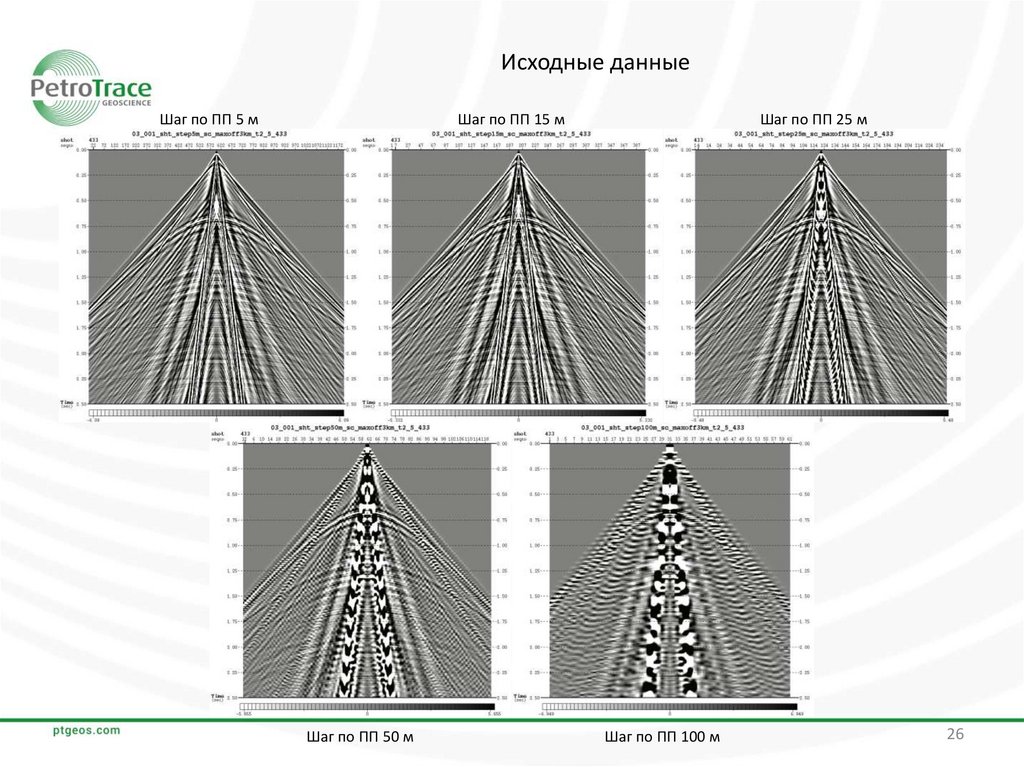
26.

Исходные данные
Шаг по ПП 5 м
Шаг по ПП 25 м
Шаг по ПП 15 м
Шаг по ПП 50 м
Шаг по ПП 100 м
26

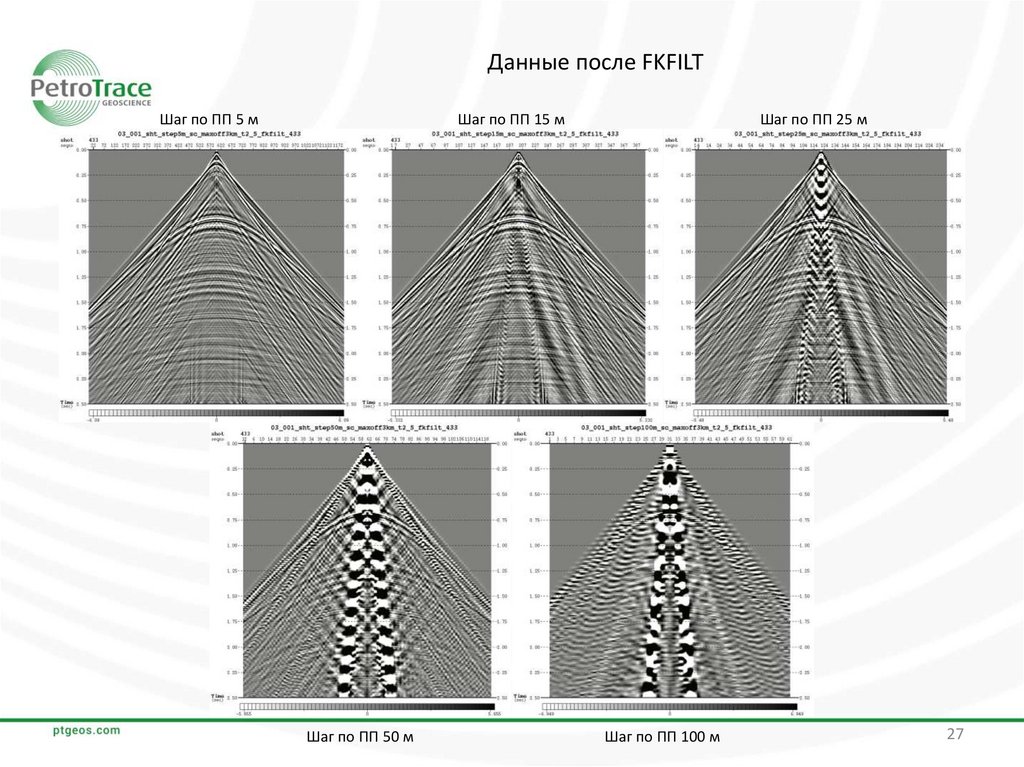
27.

Данные после FKFILT
Шаг по ПП 5 м
Шаг по ПП 25 м
Шаг по ПП 15 м
Шаг по ПП 50 м
Шаг по ПП 100 м
27

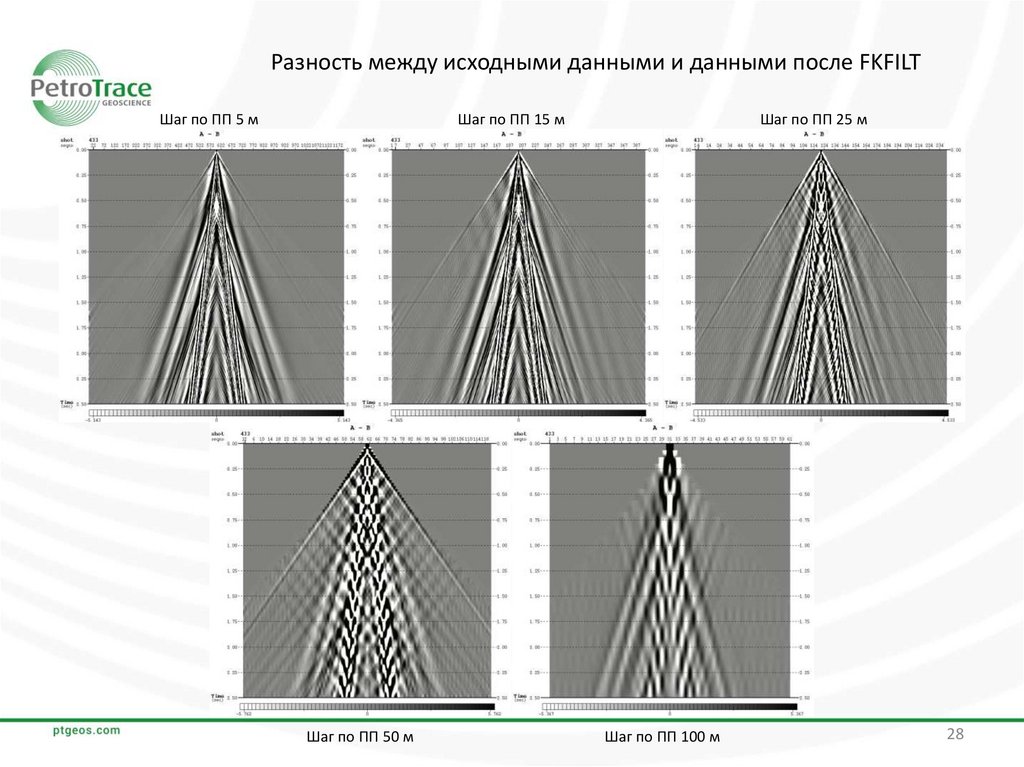
28.

Разность между исходными данными и данными после FKFILT
Шаг по ПП 5 м
Шаг по ПП 25 м
Шаг по ПП 15 м
Шаг по ПП 50 м
Шаг по ПП 100 м
28

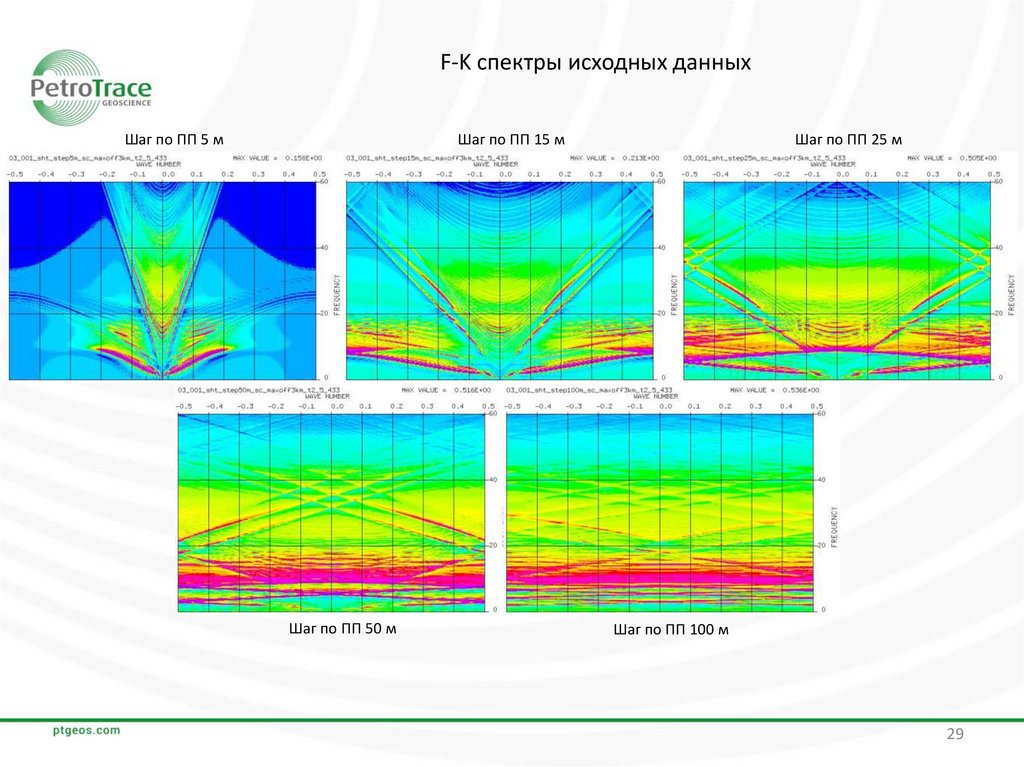
29.

F-K спектры исходных данных
Шаг по ПП 5 м
Шаг по ПП 15 м
Шаг по ПП 50 м
Шаг по ПП 25 м
Шаг по ПП 100 м
29

30.

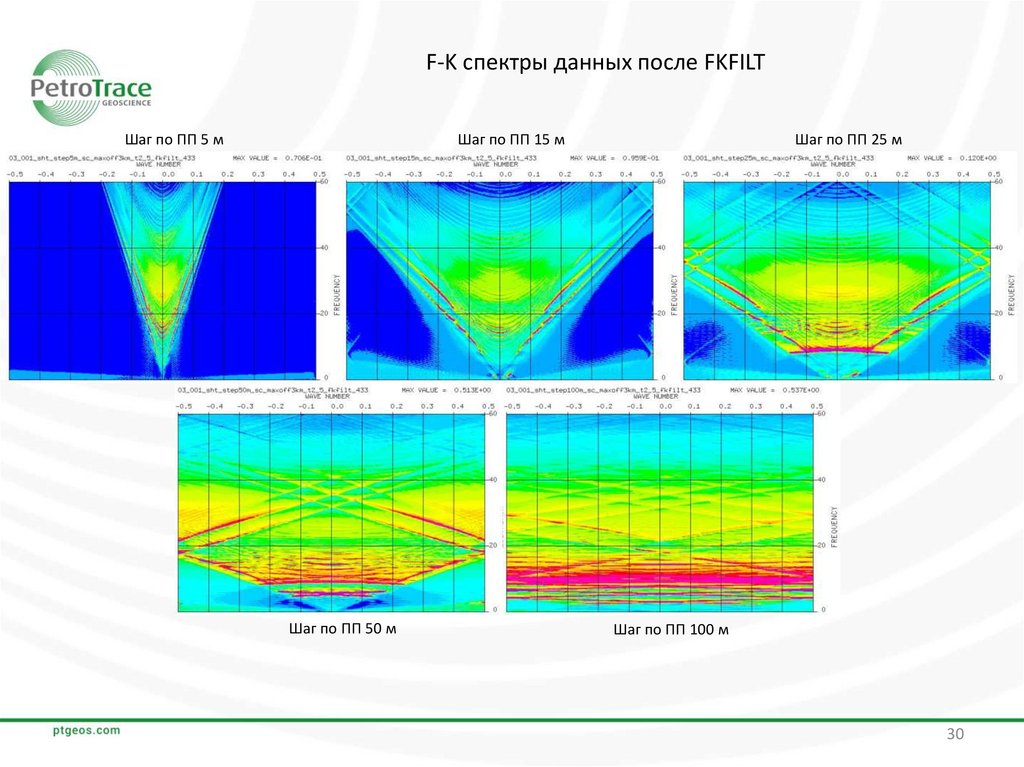
F-K спектры данных после FKFILT
Шаг по ПП 5 м
Шаг по ПП 15 м
Шаг по ПП 50 м
Шаг по ПП 25 м
Шаг по ПП 100 м
30

31.

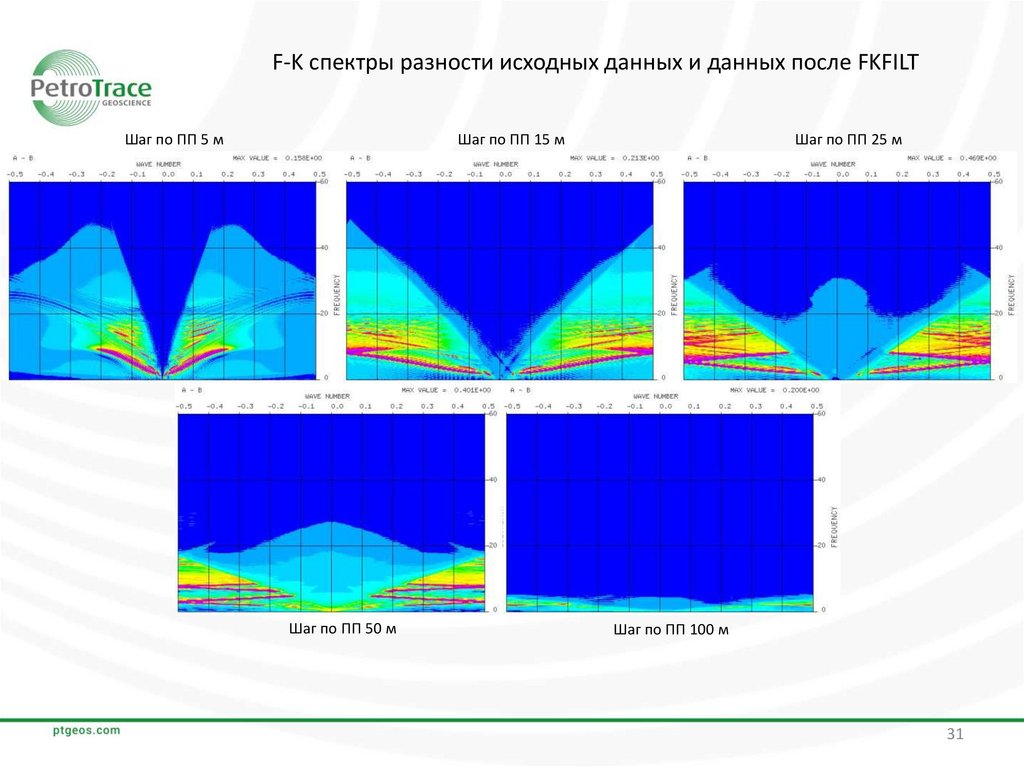
F-K спектры разности исходных данных и данных после FKFILT
Шаг по ПП 5 м
Шаг по ПП 15 м
Шаг по ПП 50 м
Шаг по ПП 25 м
Шаг по ПП 100 м
31

32.

Выводы
С увеличением шага между ПП усиливается аляйсинг-эффект на сейсмических данных. Это хорошо
видно как по сейсмическим данным, так и по F-K спектрам этих данных. По F-K спектрам исходных
данных можно сделать вывод, что аляйсинг-эффект отсутствует только на данных с шагом между ПП 5
м.
В целом, для рассмотренных алгоритмов ослабления линейных помех характерно ухудшение
результата при увеличении шага между ПП. Лучший результат получен для данных с интервалом между
ПП 5 м. В этом случае алгоритмы сработали идеально, и дополнительные инструменты для улучшения
результата не требуются. Результат ослабления волн-помех на данных с шагом по ПП 15 м также близок
к удовлетворительному.
Далее с увеличением шага между ПП наблюдается ухудшение результатов работы алгоритмов:
линейные помехи ослабляются не полностью, оставшаяся часть помех начинает «размазываться» в
виде ложных низкочастотных высокоамплитудных событий. На данных после F-K фильтрации также
появились артефакты фильтрации.
Полигоны и наклоны для F-K фильтрации линейных помех настраиваются в f-k области,
следовательно, точность и корректность их задания зависит от качества F-K изображения. Для данных с
интервалами между ПП 5-25 м аляйсинг-эффект проявляется не так сильно, линейные помехи и
полезный сигнал визуально разделяются достаточно хорошо, и задание фильтра в f-k области не
вызывает проблем. На F-K спектрах данных с интервалами 50 и 100 м между ПП линейные помехи и
полезный сигнал разделяются значительно хуже. В этих случаях задавать параметры фильтра
становится сложнее.
Кроме того, при наличии аляйсинг-эффекта в сейсмических данных часть линейных помех
интерферирует с полезным сигналом в области f-k, поэтому разделить их с помощью F-K фильтрации не
удастся. В этом смысле алгоритм LFAF обладает преимуществом перед F-K фильтрацией, поскольку
ослабляет линейные помехи в указанной области. Это хорошо видно на представленных F-K спектрах.
32

33.

На следующем этапе выполнения работ из исходного набора сейсмических данных с шагом между
ПП 5 м был получен еще один набор путем группирования приемников.
Группирование было выполнено на базе 10 приемников (45 м) встык, без перекрытий. Центр базы
соответствовал приемникам с координатами 0, 50, 100, … м. Таким образом, в полученном наборе шаг
между ПП составлял 50 м.
По полученному набору данных также выполнялось ослабление поверхностных волн алгоритмами
LFAF и FKFILT.
Далее будет представлено сопоставление полученных результатов для данных с интервалом
между ПП 50 м без группирования приемников и с группированием.
33

34.

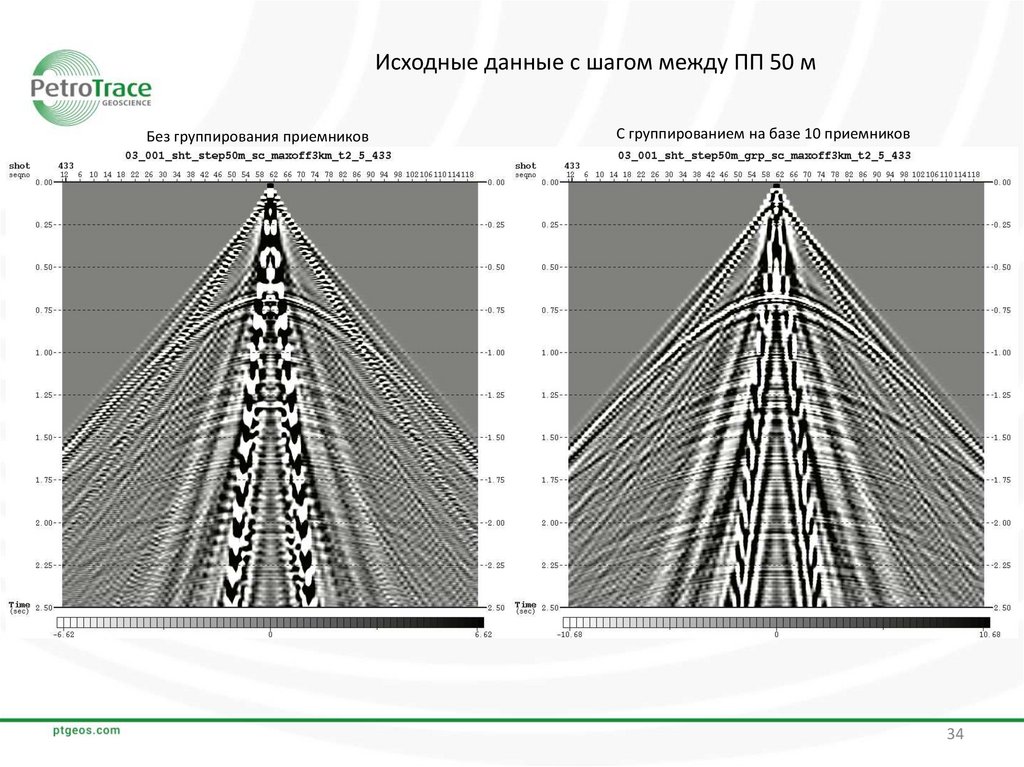
Исходные данные с шагом между ПП 50 м
Без группирования приемников
С группированием на базе 10 приемников
34

35.

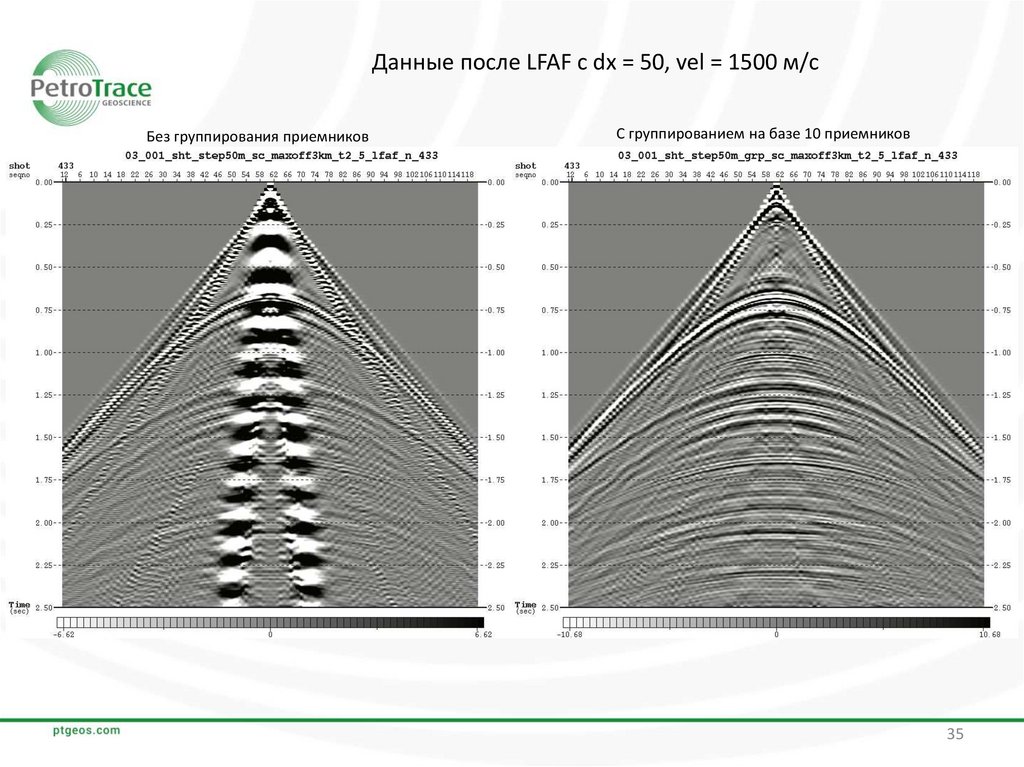
Данные после LFAF с dx = 50, vel = 1500 м/с
Без группирования приемников
С группированием на базе 10 приемников
35

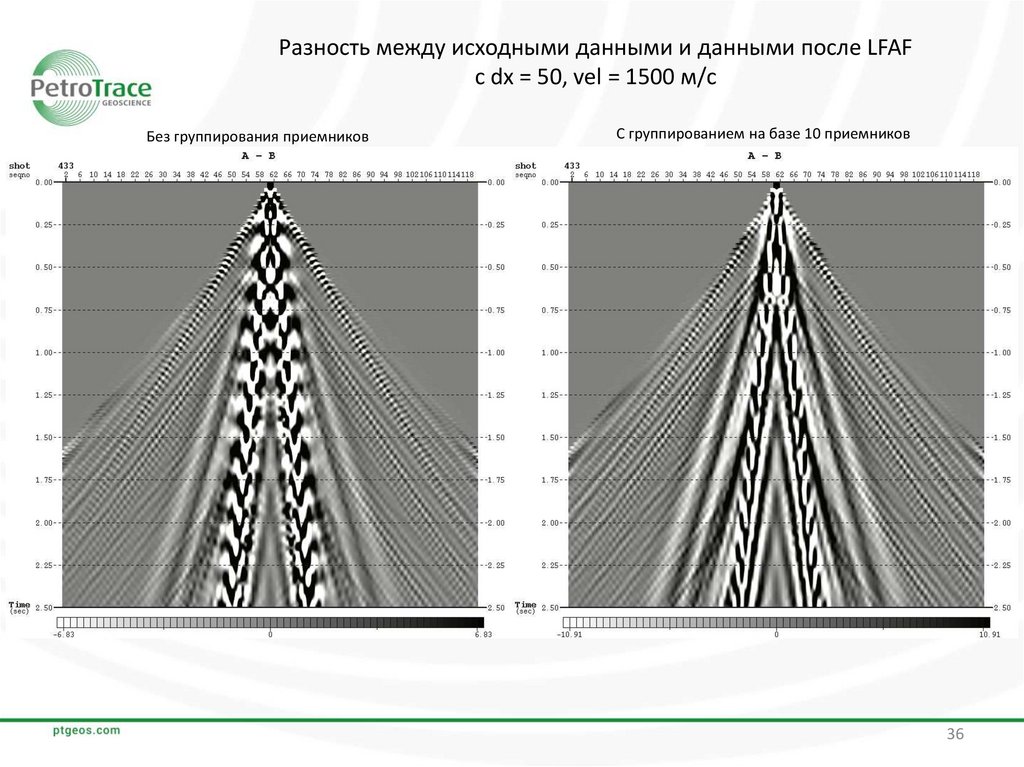
36.

Разность между исходными данными и данными после LFAF
с dx = 50, vel = 1500 м/с
Без группирования приемников
С группированием на базе 10 приемников
36

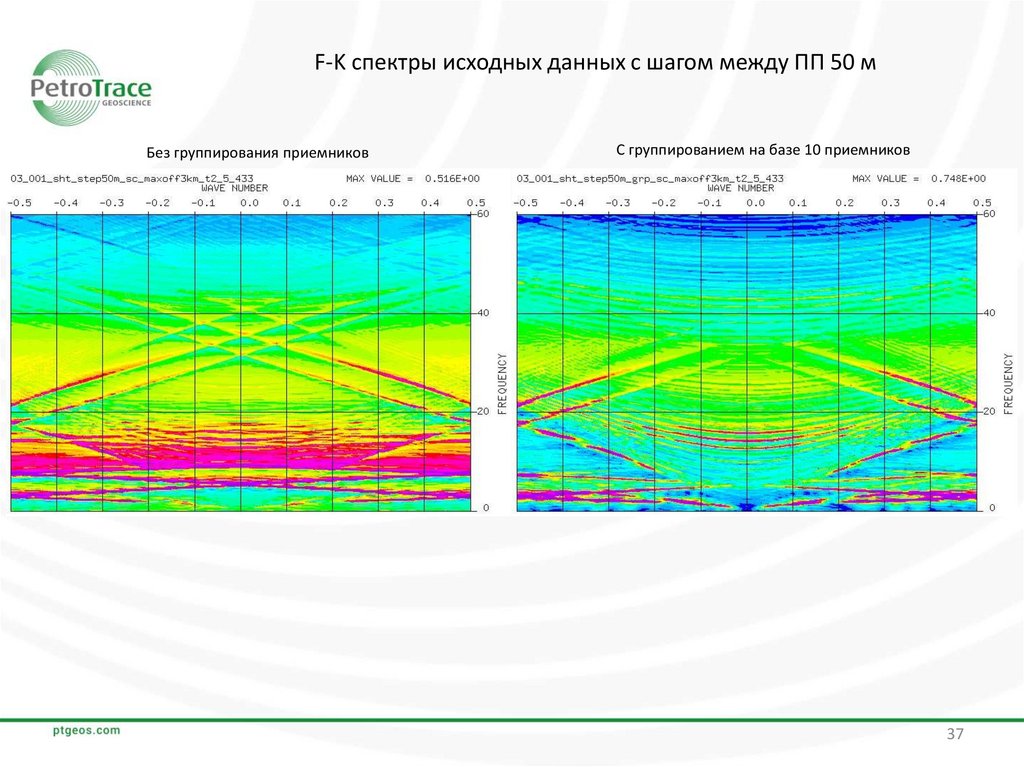
37.

F-K спектры исходных данных с шагом между ПП 50 м
Без группирования приемников
С группированием на базе 10 приемников
37

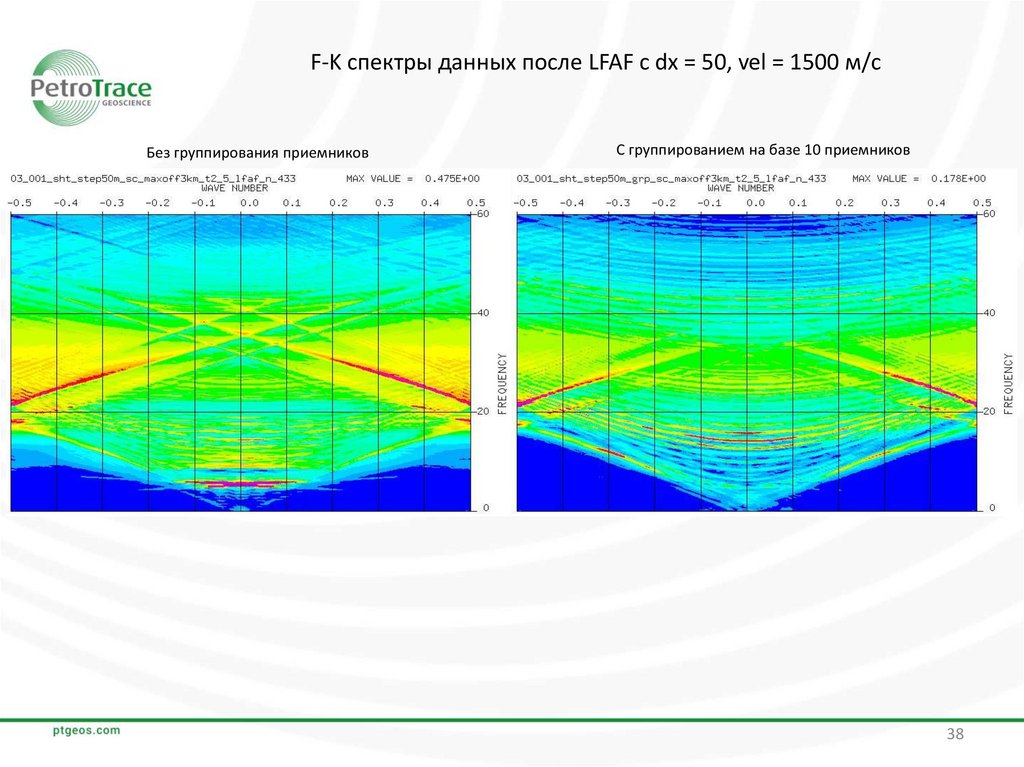
38.

F-K спектры данных после LFAF с dx = 50, vel = 1500 м/с
Без группирования приемников
С группированием на базе 10 приемников
38

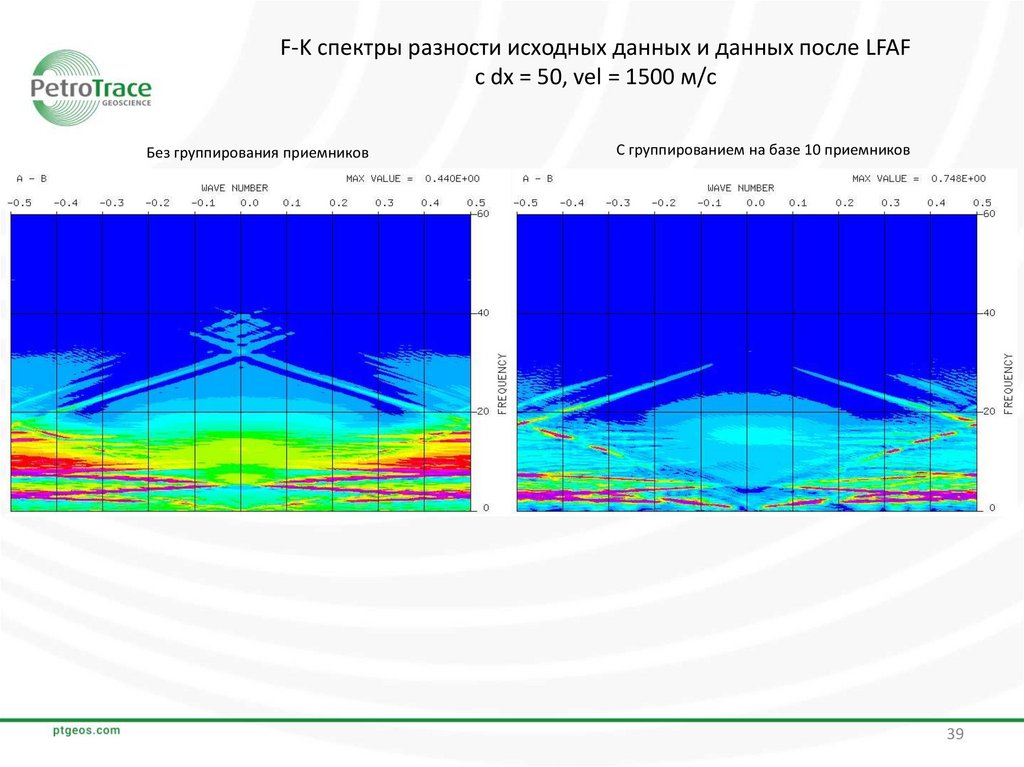
39.

F-K спектры разности исходных данных и данных после LFAF
с dx = 50, vel = 1500 м/с
Без группирования приемников
С группированием на базе 10 приемников
39

40.

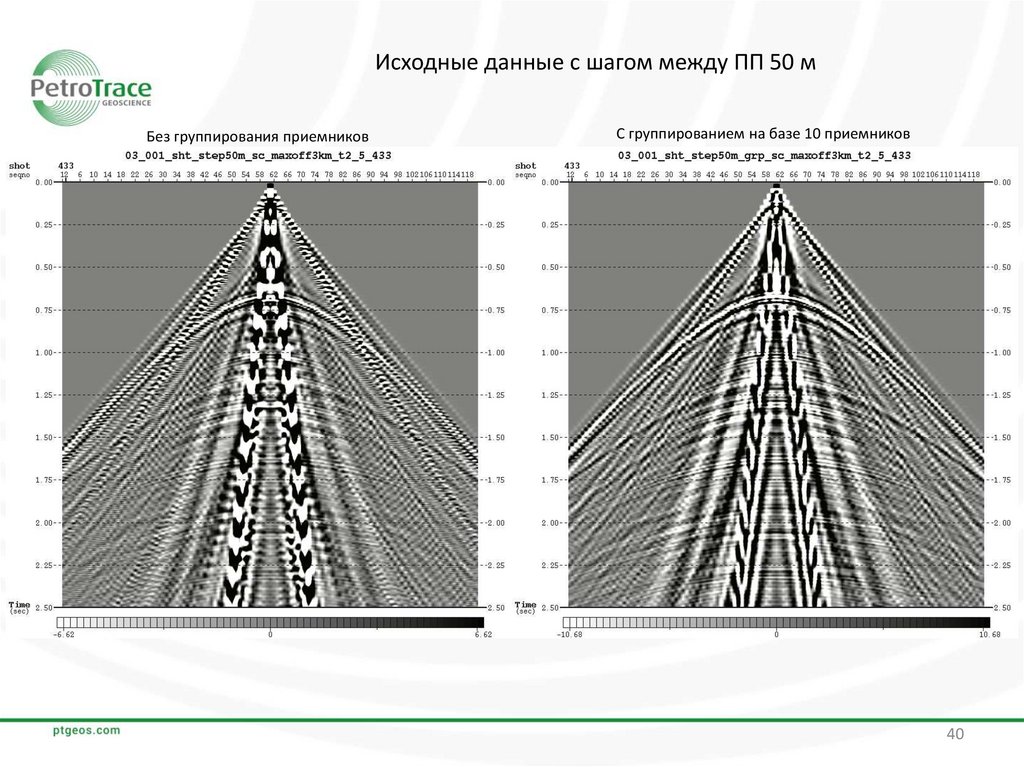
Исходные данные с шагом между ПП 50 м
Без группирования приемников
С группированием на базе 10 приемников
40

41.

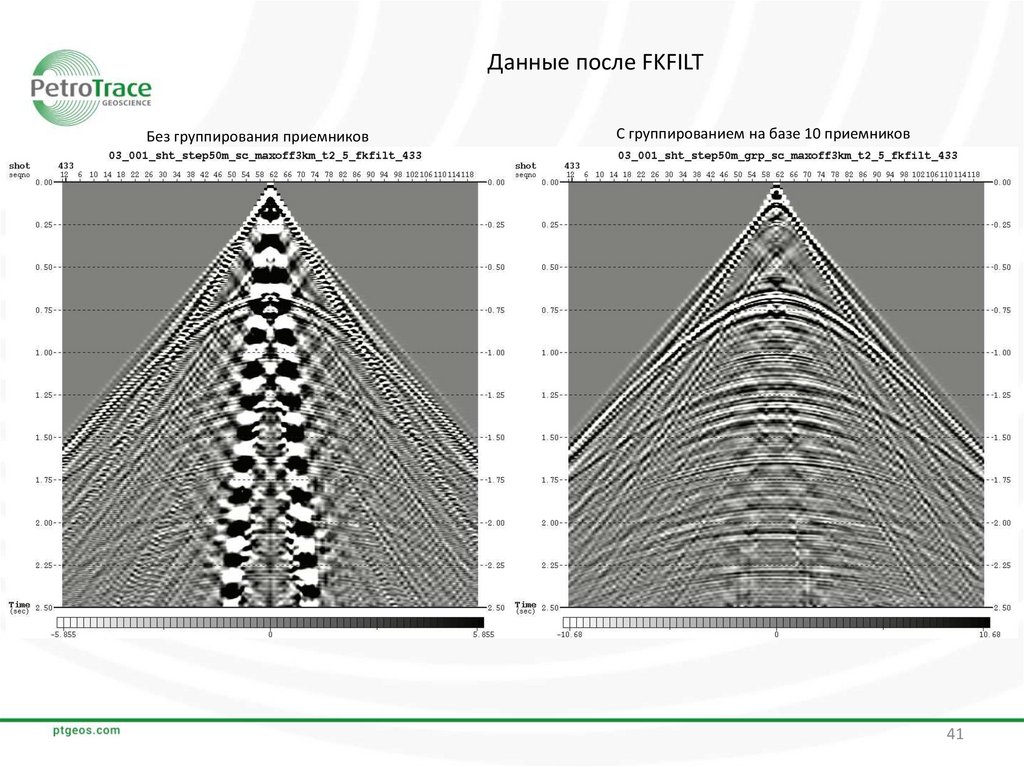
Данные после FKFILT
Без группирования приемников
С группированием на базе 10 приемников
41

42.

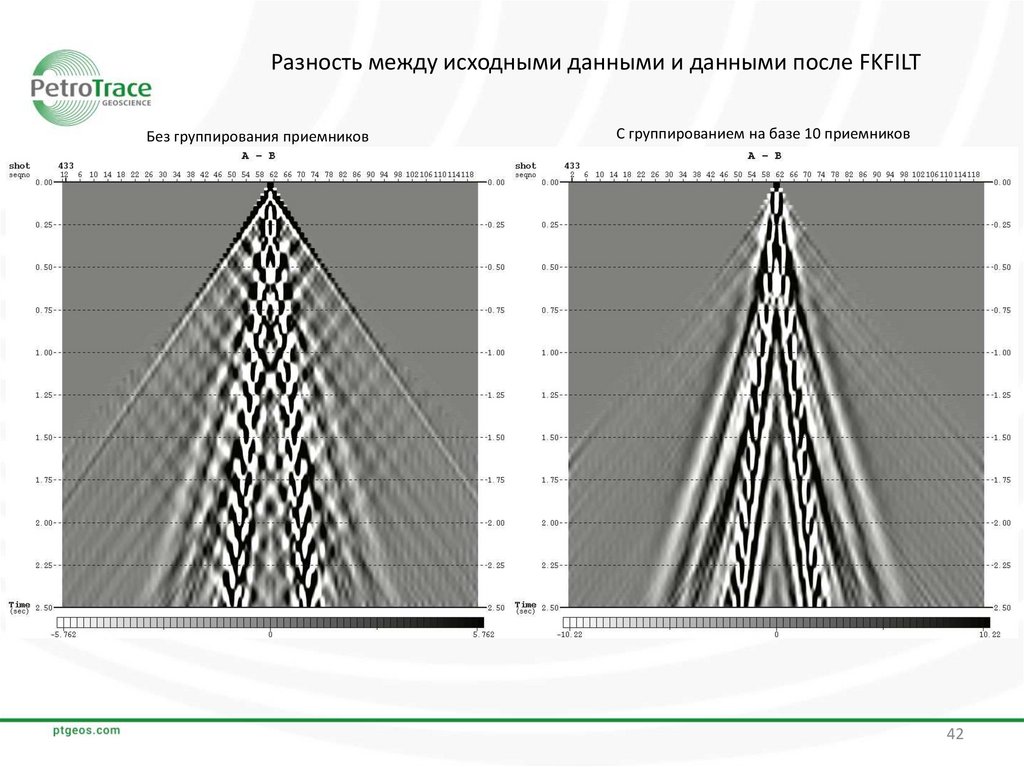
Разность между исходными данными и данными после FKFILT
Без группирования приемников
С группированием на базе 10 приемников
42

43.

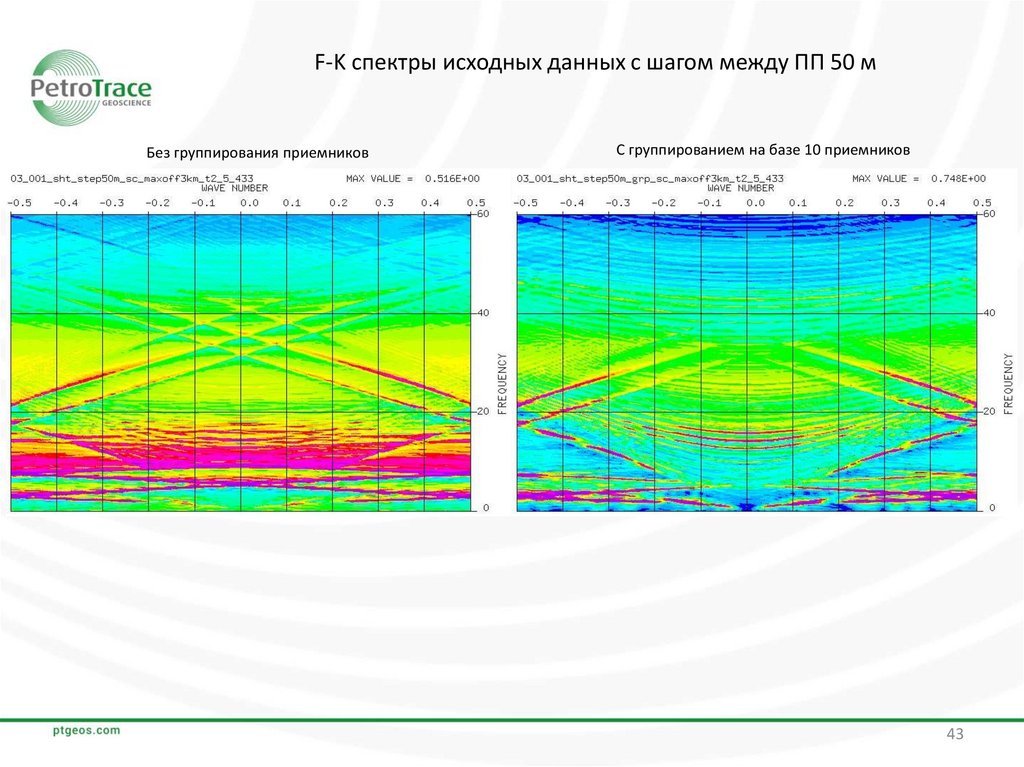
F-K спектры исходных данных с шагом между ПП 50 м
Без группирования приемников
С группированием на базе 10 приемников
43

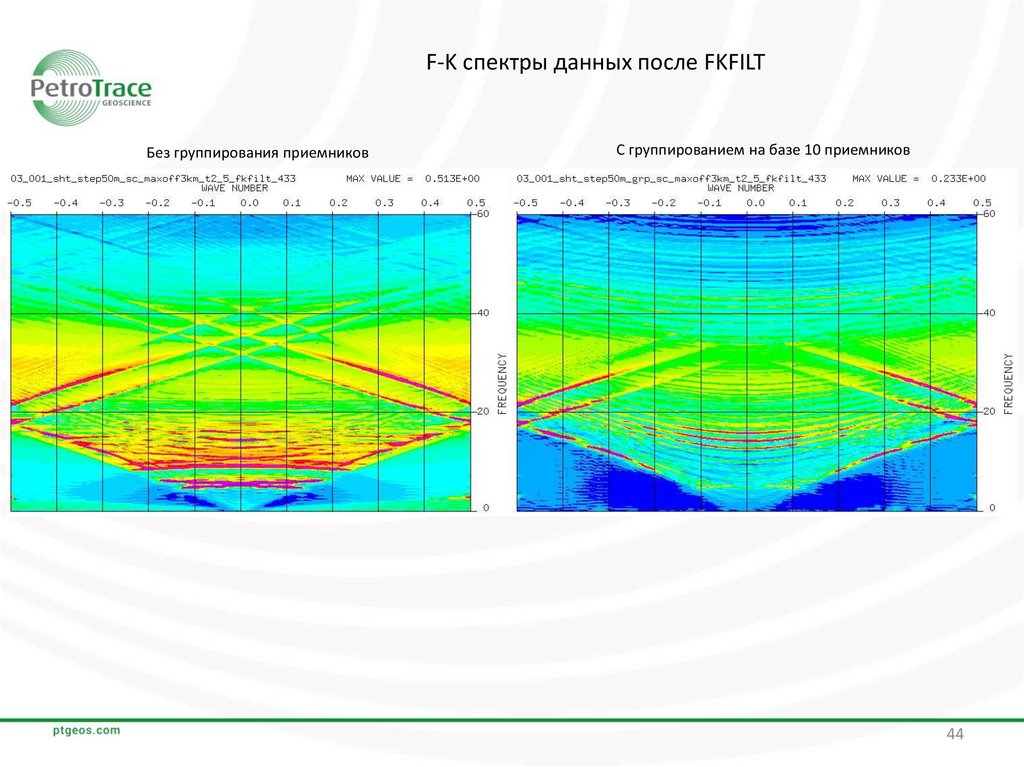
44.

F-K спектры данных после FKFILT
Без группирования приемников
С группированием на базе 10 приемников
44

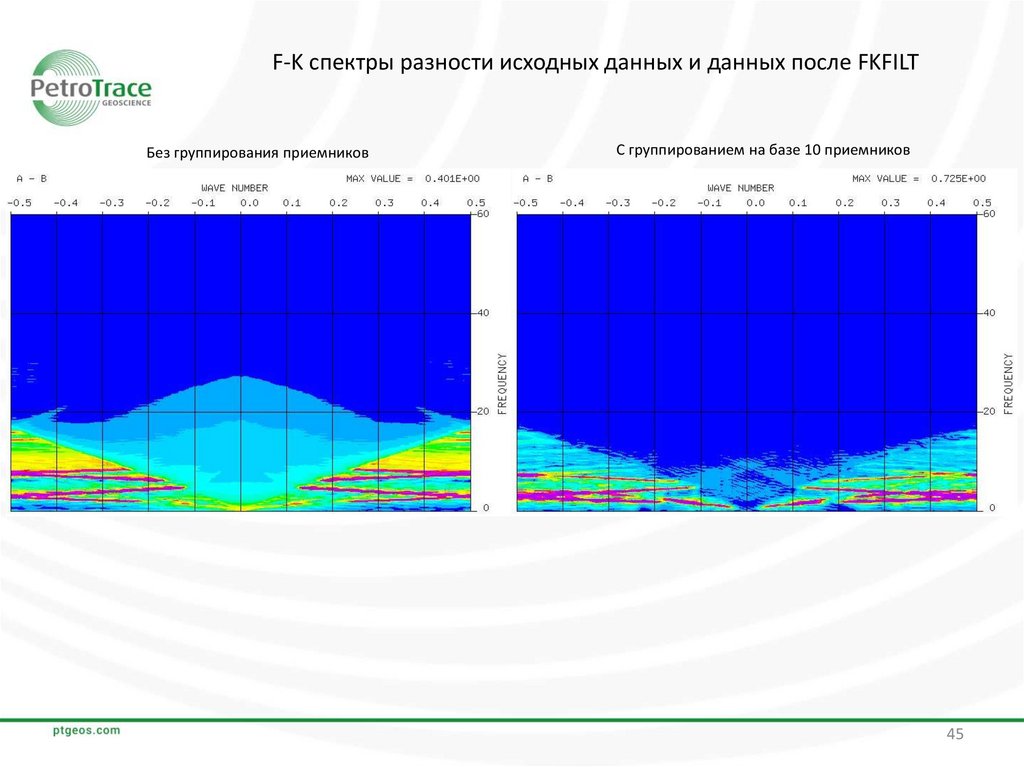
45.

F-K спектры разности исходных данных и данных после FKFILT
Без группирования приемников
С группированием на базе 10 приемников
45

46.

Выводы
При сравнении полученных результатов становится очевидной роль группирования сейсмических
приемников в целях ослабления аляйсинг-эффекта.
По исходным сейсмограммам и рассчитанным по ним F-K спектрам видно, что данные с
группированием приемников в значительно меньшей степени подвержены влиянию аляйсинг-эффекта
по сравнению с данными без группирования.
Результаты ослабления поверхностных волн с помощью алгоритма LFAF и F-K фильтрации
показывают возможность полного ослабления волн-помех на данных с группированием. При этом на
сейсмограммах без группирования значительная часть помех остается в данных в искаженном из-за
присутствия аляйсинг-эффекта виде.
Поскольку в данных с шагом 25 м без группирования аляйсинг-эффект проявляется не так сильно, с
помощью дополнительных процедур обработки возможно улучшить полученный результат ослабления
поверхностных волн до удовлетворительного.
Подводя итог, считаем более оптимальным при проведении полевых работ использовать шаг
между ПП 25 м в случае отсутствия группирования сейсмоприемников или 50 м с линейным
группированием.
46

47.

Применение некоторых процедур временной обработки к
модельным сейсмическим данным 2D
47

48.

Введение
В рамках данного этапа по синтетическим сейсмическим данным 2Д выполнялись следующие
процедуры временной обработки:
- ослабление линейных помех с помощью модуля LFAF;
- коррекция кинематических поправок (скоростной анализ) и статических поправок (MASTT, Techco
Geophysical);
- ослабление кратных волн с помощью параболического преобразования Радона (RADNPAR).
Исходные данные – модельные сейсмограммы с группированием на базе 10 приемников (45 м).
48

49.

Ослабление линейных помех с помощью модуля LFAF
Для ослабления поверхностных волн на исходном наборе модельных данных использовалась
низкочастотная фильтрация массива (LFAF).
Программа LFAF осуществляет ослабление линейных помех по следующему алгоритму:
1. Преобразование сейсмограмм из области t-x в область f-x;
2. Свертка каждой частотной компоненты из заданного частотного диапазона (диапазона, в
котором требуется ослабить линейные волны-помехи) с прямоугольной функцией определенной
длины;
3. Обратное преобразование сейсмограмм из области f-x в область t-x.
Перед применением процедуры LFAF в данные вводились статические и кинематические поправки.
Программа выполнялась во всем диапазоне частот со следующими значениями параметров:
пространственный шаг дискретизации dx = 50, скорость поверхностных волн vel = 1500 м/с.
49

50.

Ослабление линейных помех с помощью модуля LFAF
Пример сейсмограмм ОПВ до подавления поверхностных волн
50

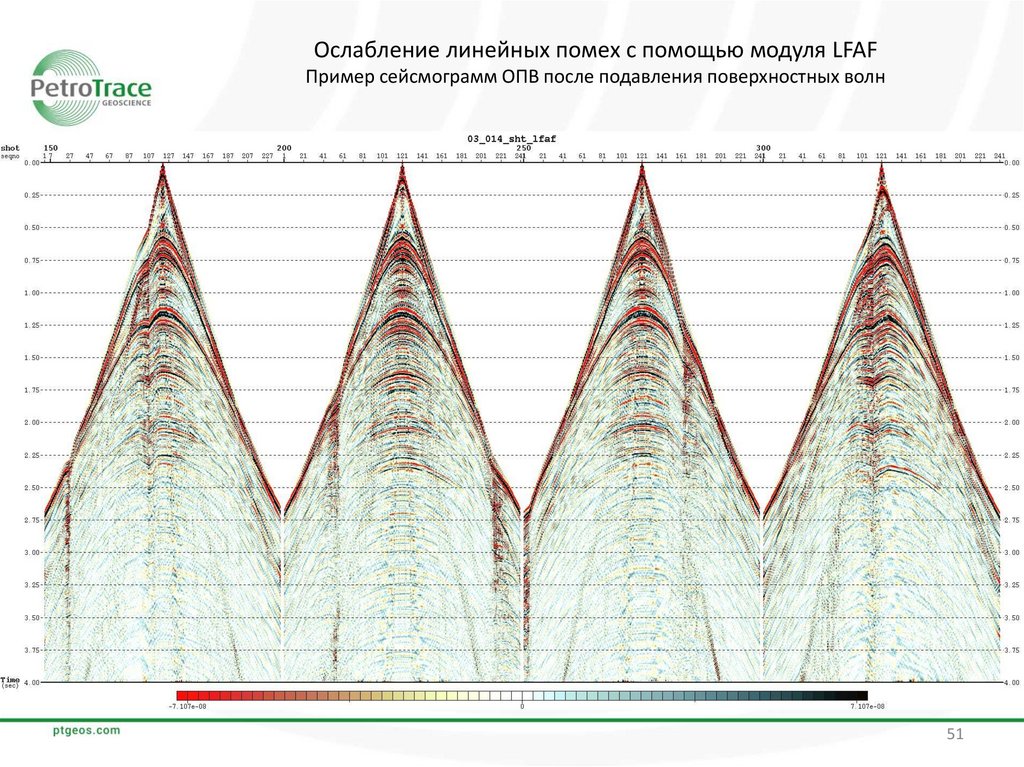
51.

Ослабление линейных помех с помощью модуля LFAF
Пример сейсмограмм ОПВ после подавления поверхностных волн
51

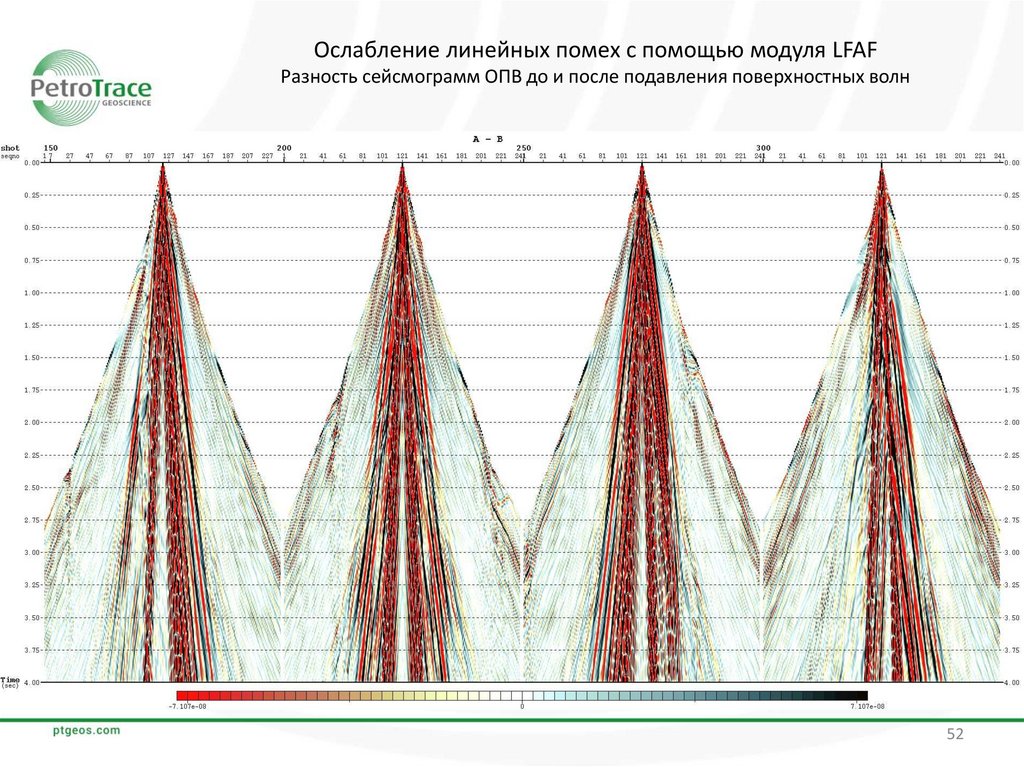
52.

Ослабление линейных помех с помощью модуля LFAF
Разность сейсмограмм ОПВ до и после подавления поверхностных волн
52

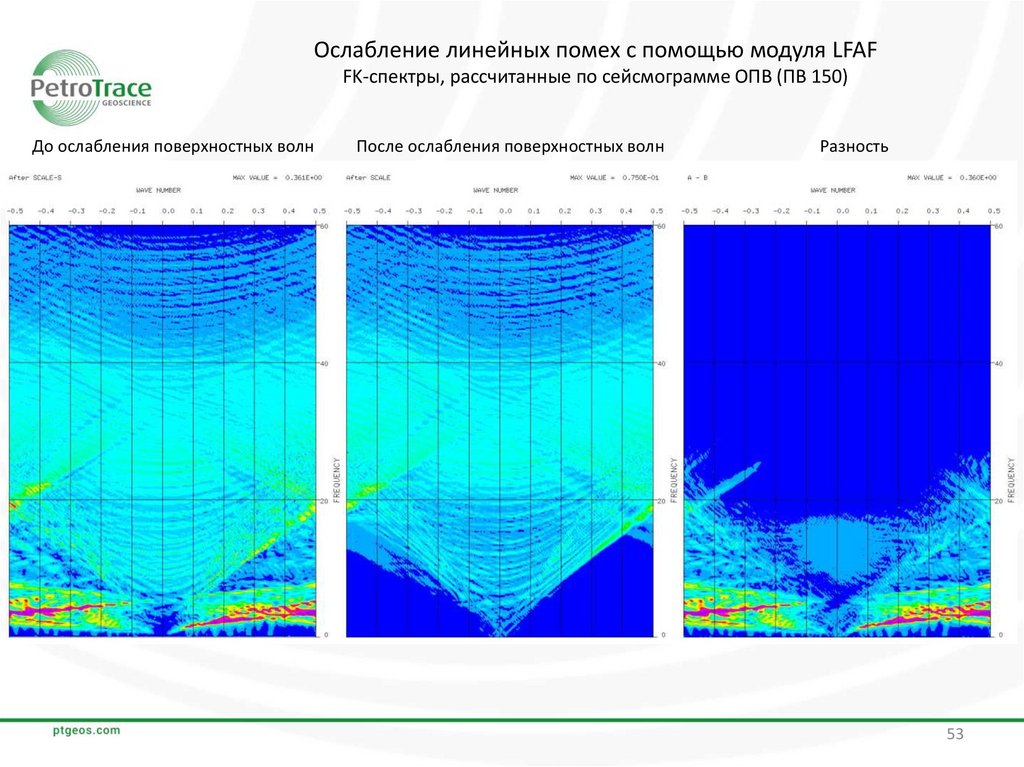
53.

Ослабление линейных помех с помощью модуля LFAF
FK-спектры, рассчитанные по сейсмограмме ОПВ (ПВ 150)
До ослабления поверхностных волн
После ослабления поверхностных волн
Разность
53

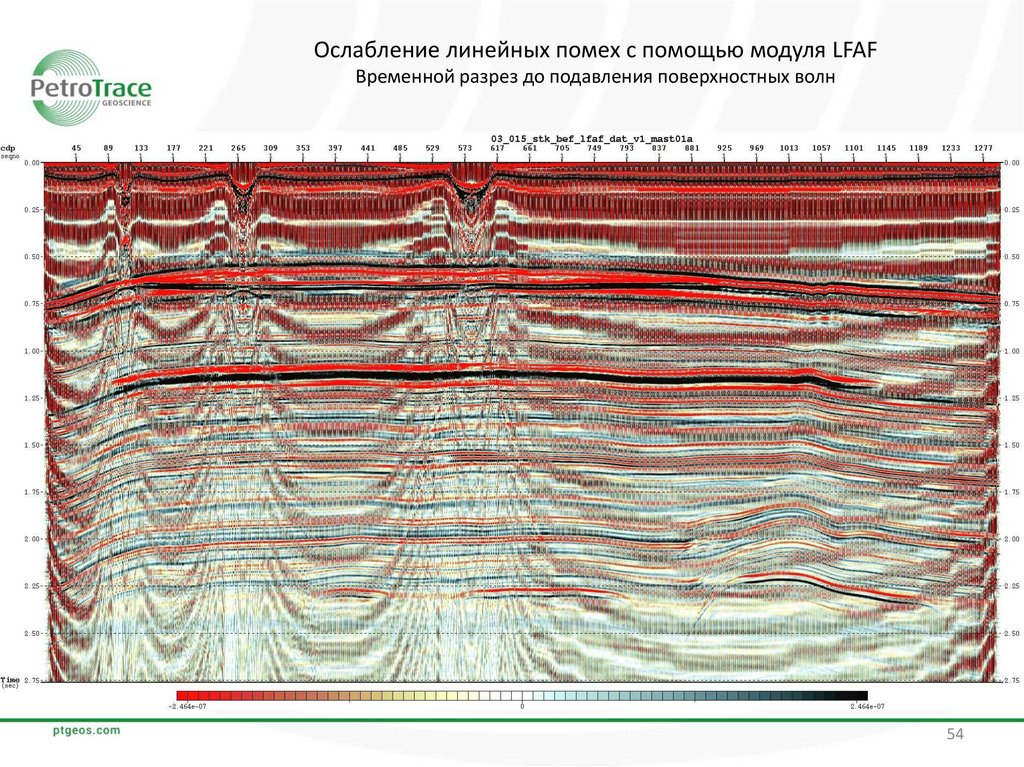
54.

Ослабление линейных помех с помощью модуля LFAF
Временной разрез до подавления поверхностных волн
54

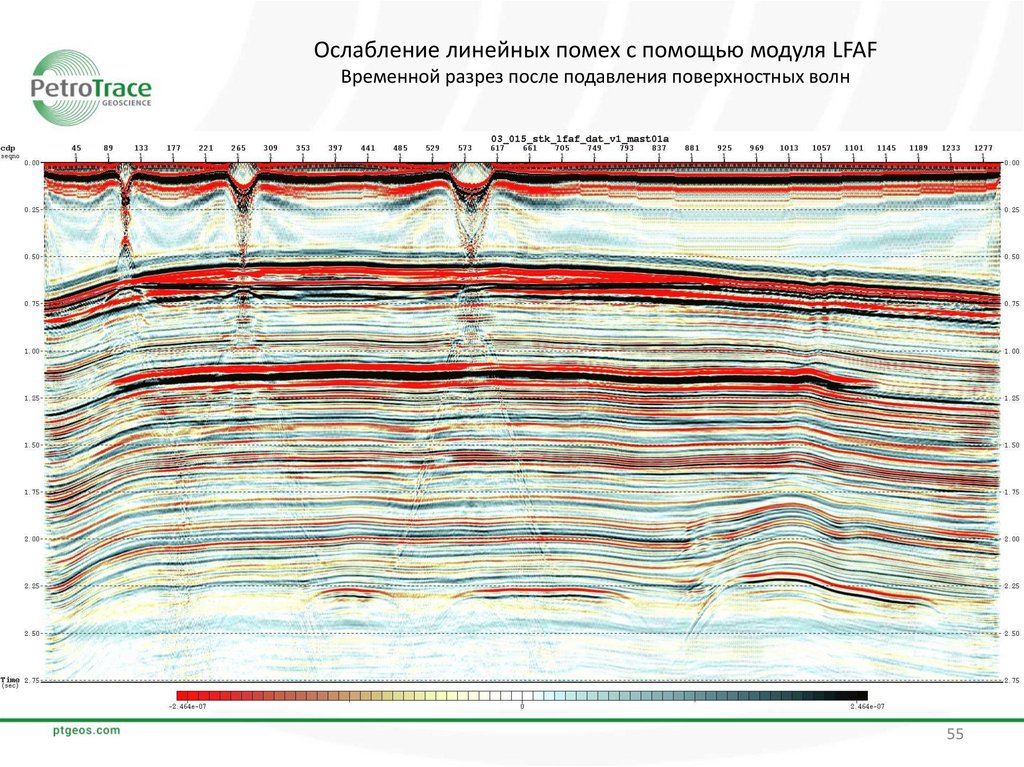
55.

Ослабление линейных помех с помощью модуля LFAF
Временной разрез после подавления поверхностных волн
55

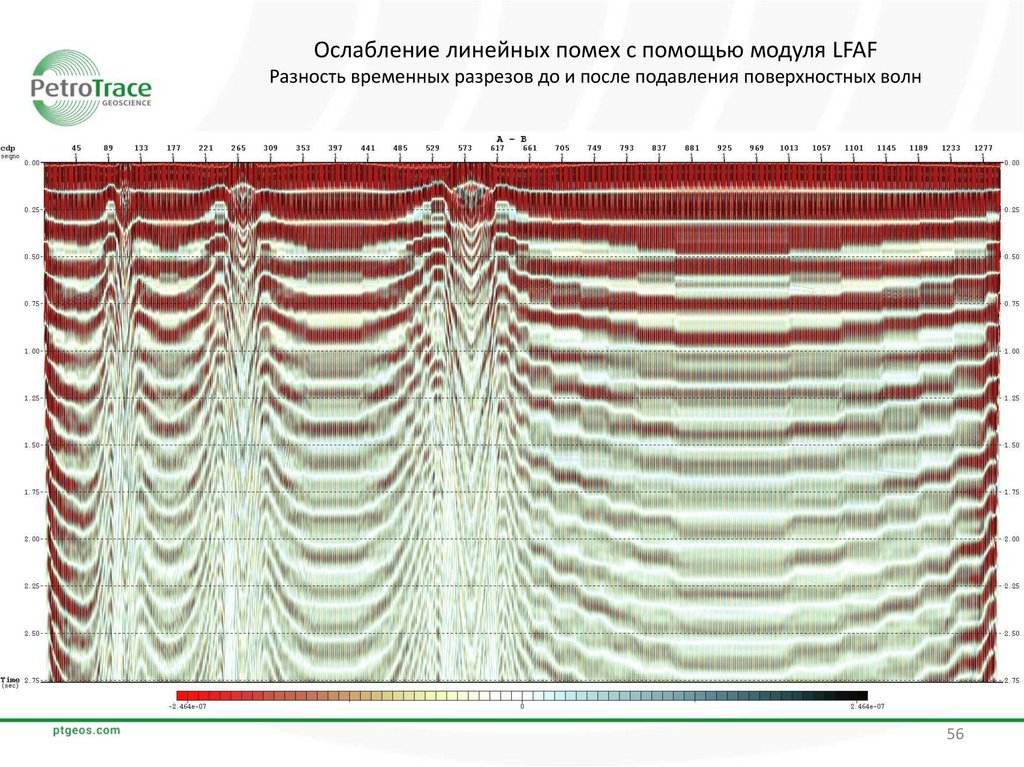
56.

Ослабление линейных помех с помощью модуля LFAF
Разность временных разрезов до и после подавления поверхностных волн
56

57.

Коррекция кинематических и статических поправок
В качестве априорных статических поправок были взяты статические поправки, рассчитанные по
преломленным волнам в программном комплексе Flatirons (XtremeGeo) (этот этап детально
представлен в отдельной презентации).
Анализ скоростей суммирования выполнялся с шагом 100 ОГТ. Для улучшения визуализации и
повышения качества пикировок скоростей формировались суперподборки ОГТ с переменной базой
(максимальная база – 21 ОГТ).
Для автоматического расчета остаточных статических поправок использовалась программа MASTT
(Techco Geophysical). В программе используется критерий выбора медианного значения сдвига
максимума ФВК. Это позволяет избегать локальных максимумов ФВК («переходов на фазу») при
наличии высокоамплитудных статических сдвигов.
57

58.

Коррекция кинематических и статических поправок
Временной разрез, полученный с начальными скоростями суммирования
(заданными в одной точке)
58

59.

Коррекция кинематических и статических поправок
Временной разрез, полученный с финальными скоростями суммирования
(после скоростного анализа с шагом 100 ОГТ)
59

60.

Коррекция кинематических и статических поправок
Временной разрез после автоматической коррекции статических поправок
(получен с финальными скоростями суммирования)
60

61.

Ослабление кратных волн с помощью параболического преобразования Радона
Ослабление кратных волн выполнялось с помощью модуля RADNPAR. RADNPAR осуществляет
параболическое преобразование Радона по сейсмограммам ОГТ с введенной кинематикой. При
введении корректной кинематики ожидается, что годографы однократных отражений спрямятся, а у
годографов многократных отражений будет наблюдаться недоспрямление или переспрямление. На
основе этих кинематических отличий можно разделить однократные и многократные события в tau-p
области и выполнить ослабление кратных волн.
RADNPAR преобразует данные из области t-x в область tau-p. После прямого преобразования в
область tau-p программа либо обнуляет заданную пользователем область однократно отраженных
волн, выполняет обратное преобразование в область t-x оставшейся энергии кратных волн и вычитает
полученный результат из исходных данных, либо обнуляет заданную пользователем область кратных
отраженных волн, выполняет обратное преобразование в область t-x оставшейся энергии однократно
отраженных волн и заменяет исходные данные данными после ослабления кратных волн.
По результатам тестирования процедуры RADNPAR преобразование данных в tau-p область
осуществлялось со следующими параметрами: максимальное удаление – 6000 м, минимальный
кинематический сдвиг – -150 мс, максимальный кинематический сдвиг – 1200 мс, количество парабол в
трансформации – 351.
Затем в области tau-p применялся фильтр с кинематическими сдвигами в диапазоне (-150)-150 мс
на удалении 6000 м для вычитания полезных отражений (количество парабол в трансформации – 150).
Полученная модель шума адаптивно вычиталась из исходных сейсмограмм при трансформации во
временную область.
61

62.

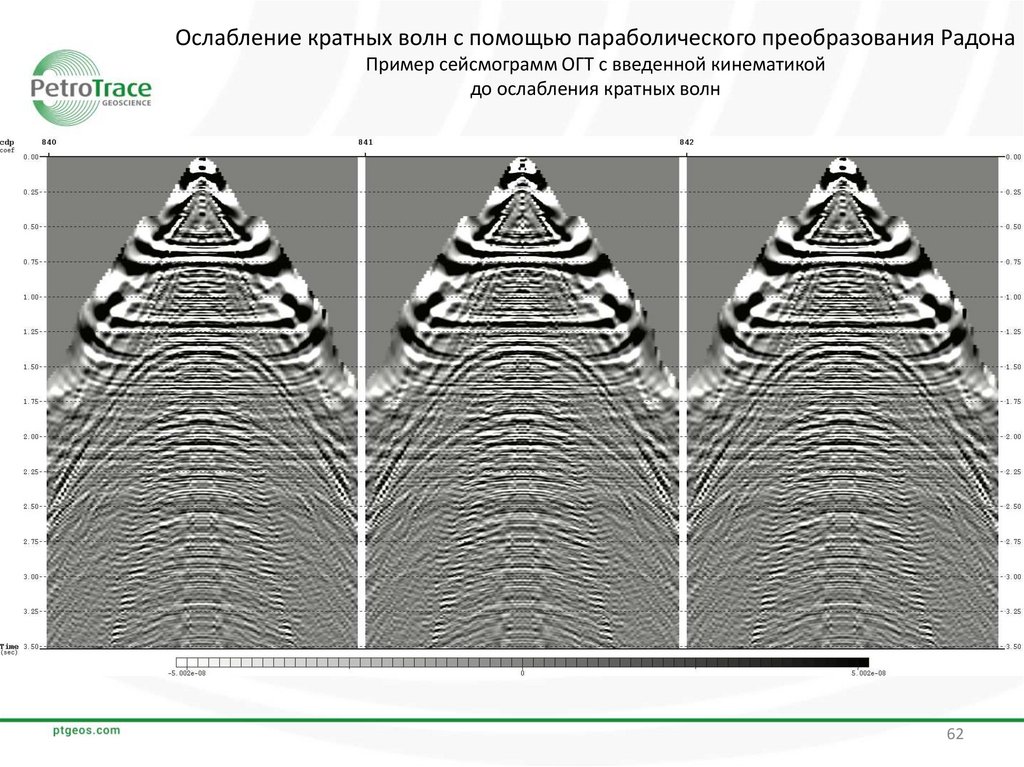
Ослабление кратных волн с помощью параболического преобразования Радона
Пример сейсмограмм ОГТ с введенной кинематикой
до ослабления кратных волн
62

63.

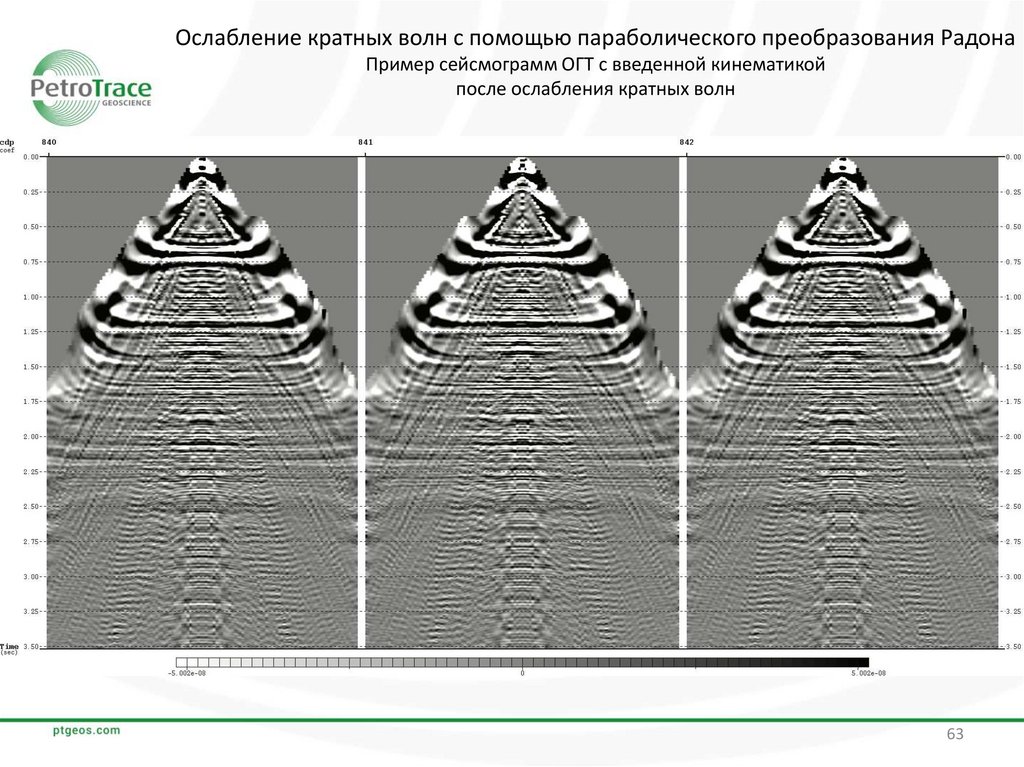
Ослабление кратных волн с помощью параболического преобразования Радона
Пример сейсмограмм ОГТ с введенной кинематикой
после ослабления кратных волн
63

64.

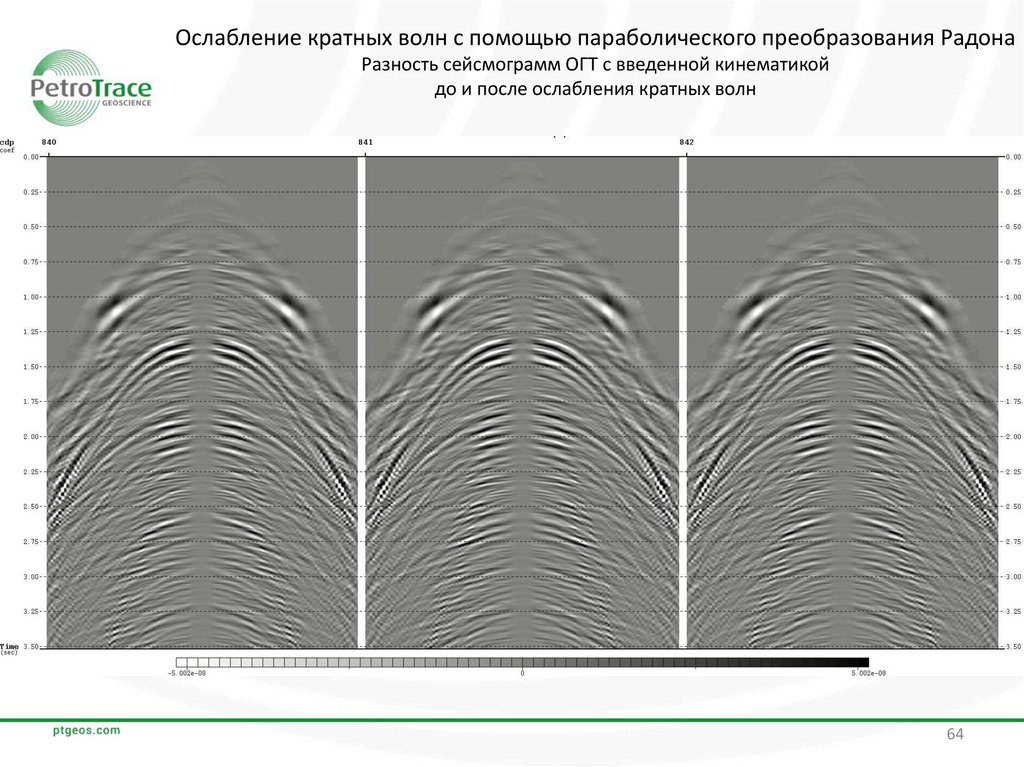
Ослабление кратных волн с помощью параболического преобразования Радона
Разность сейсмограмм ОГТ с введенной кинематикой
до и после ослабления кратных волн
64

65.

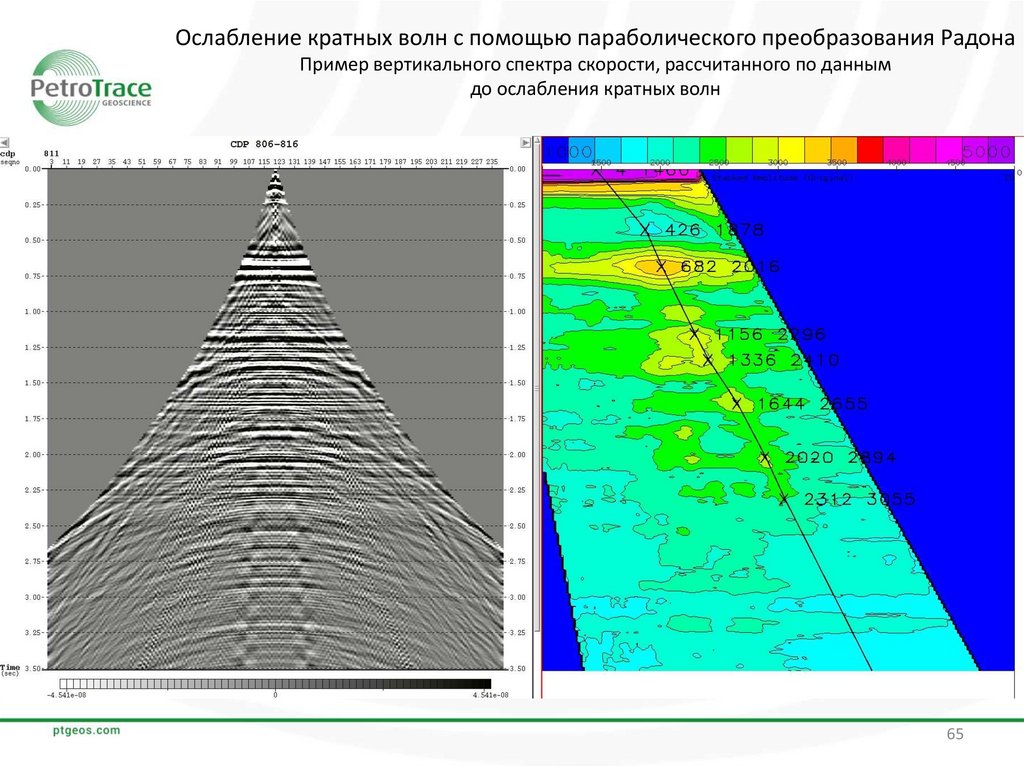
Ослабление кратных волн с помощью параболического преобразования Радона
Пример вертикального спектра скорости, рассчитанного по данным
до ослабления кратных волн
65

66.

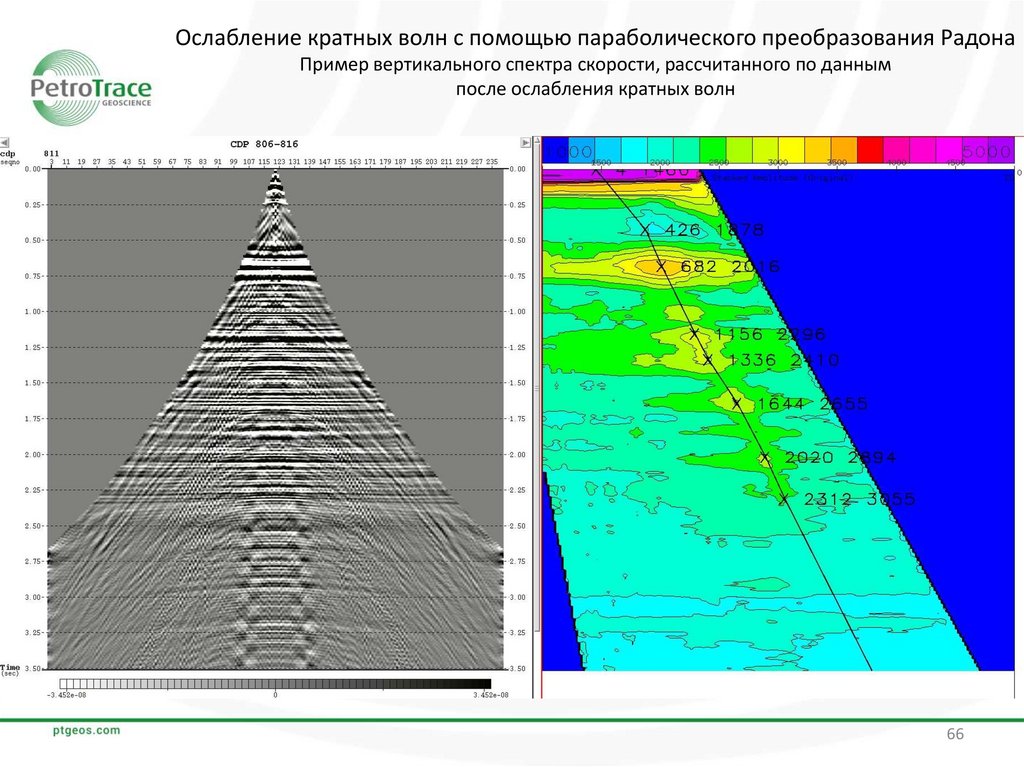
Ослабление кратных волн с помощью параболического преобразования Радона
Пример вертикального спектра скорости, рассчитанного по данным
после ослабления кратных волн
66

67.

Выводы
По набору модельных сейсмограмм 2Д выполнены следующие процедуры временной обработки:
ослабление поверхностных волн, коррекция кинематических и статических поправок, ослабление
кратных волн.
С помощью процедуры низкочастотной фильтрации массива LFAF удалось в значительной степени
ослабить поверхностные волны.
В результате выполнения интерактивного анализа скоростей суммирования и автоматической
коррекции остаточных статических поправок удалось улучшить прослеживаемость отражающих
горизонтов без изменения глобального структурного плана.
На сейсмограммах ОГТ, а также на вертикальных спектрах скоростей до и после подавления
кратных волн видно, что энергия, соответствующая кратным отражениям, значительно ослабла после
применения преобразования Радона.
67

68.

СПАСИБО ЗА ВНИМАНИЕ
ПетроТрейс Москва
PetroTrace London
РФ, 115114, Москва, Летниковская ул. 10, стр.4
Бизнес-центр «Святогор-4», 6 этаж
PetroTrace Ltd
Dukes Court, Woking, Surrey,
UK, GU21 5BH
тел.: +7 495 995 5230
факс: +7 495 995 5232
e: [email protected]
t: +44 (0)1483 662 421
e: [email protected]