Теория вероятности и комбинаторные правила для решение задач ЕГЭ В10

1.

Теория вероятности и
комбинаторные правила
для решение задач ЕГЭ В10
Белянская Елена Валентиновна
учитель математики ГБОУ СОШ №5
ОЦ «Лидер» г.о.Кинель

2.

Справочный
материал
Случайное событие (СС)- это событие, которое либо произойдёт,
либо нет.
Испытание – любое действие, которое может привести к одному
или нескольким результатам.
Исход - конечный результат испытания. Значит испытание
может иметь один или несколько исходов.
Например:
1) Бросаете монету – это испытание.
Исходы – орёл, решка.
2) Подбросили кубик (иногда называют игральной костью) –
это испытание.
Выпасть может 1, 2, 3, 4, 5 или 6 – это исходы.

3.

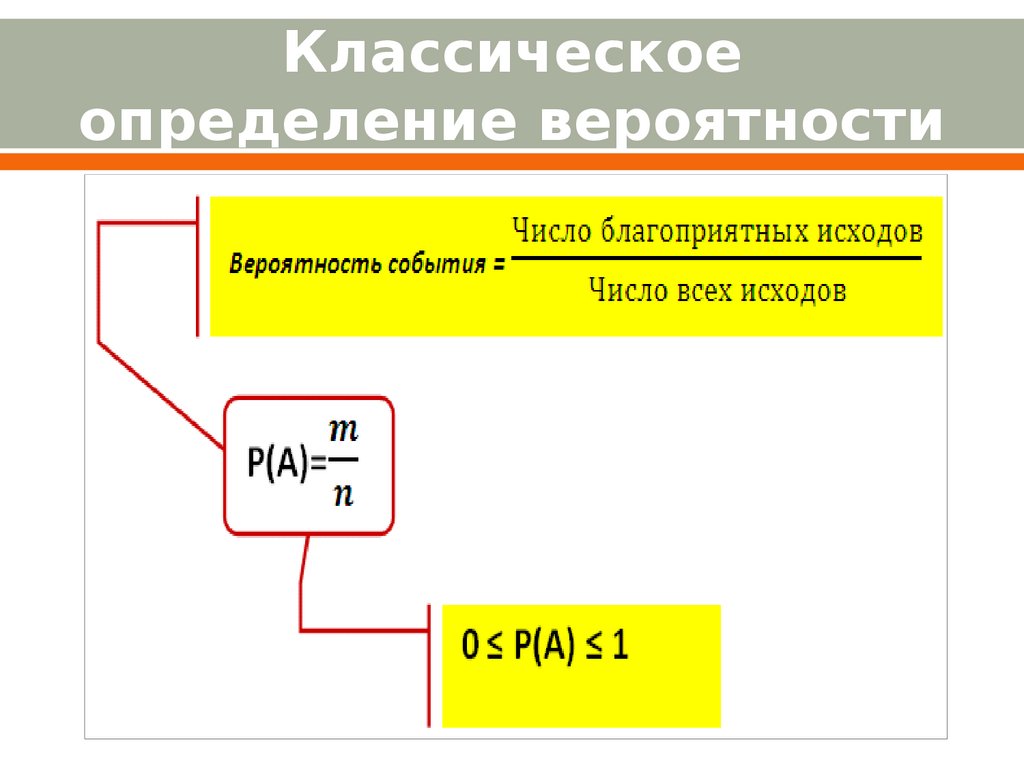
Классическое
определение вероятности

4.

Задача 1. Игральный кубик бросили один раз.
Какова вероятность того, что выпало число очков,
не менее 4.
Решение:
Случайный эксперимент – бросание кубика.
Элементарное событие – число на выпавшей грани.
Всего граней:
N=6
Элементарные события:
1, 2, 3, 4, 5, 6
N(A)=3
N ( A) 3 1
P( A)
N
6 2
Ответ:0,5

5.

Задача 2. В чемпионате по гимнастике
участвуют 50 спортсменок: 24 из США, 13
из Мексики, остальные — из Канады.
Порядок, в котором выступают гимнастки,
определяется
жребием.
Найдите
вероятность
того,
что
спортсменка,
Решение:
выступающая
первой,– выступление
окажется
из
Случайный эксперимент
спортсменок
Канады.
Элементарное событие – выступающая первой, окажется
из Канады
Число элементарных событий: N=50
Событие А = {выспупающая первой, окажется из Канады},
N(A)= m=50-(24+13)=13
N ( A) 13
P( A)
0,26
N
50
Ответ: 0,26

6.

Задача 3.
В чемпионате мира участвуют 4 группы 16 команд. С
помощью жребия их нужно разделить на группы по 4
команды в каждой. В ящике вперемешку лежат карточки с
номерами групп:
1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4.
Капитаны команд тянут по одной карточке. Какова
вероятность того, что команда России окажется во второй
группе.
Решение:
Множество элементарных событий: N=16
A={команда России во второй группе}
С номером «2» четыре карточки: N(A)=4
N ( A) 4
P( A)
0,25
N
16
Ответ: 0,25

7.

Задача 4. В случайном эксперименте бросают три игральные
кости. Найти вероятность того, что в сумме выпадет 7 очков.
Результат округлите до сотых.
Эксперимент: бросают три игральные кости.
Благоприятное событие А: в сумме выпало 7 очков.
Количество
благоприятных
событий m=?
331 223 511
313 232 151
133 322 115
412 142
421 214
124 241
Количество всех событий группы n=?
1-я кость - 6 вариантов
2-я кость - 6 вариантов
3-я кость - 6 вариантов
18
6 6 6 216
m 18
Р ( А)
0,08
n 216
7

8.

Задача 5. Конкурс исполнителей проводится в 5 дней.
Всего заявлено 80 выступлений — по одному от каждой
страны. В первый день 8 выступлений, остальные
распределены поровну между оставшимися днями.
Порядок выступлений определяется жеребьёвкой.
Какова вероятность, что выступление представителя
России состоится в третий день конкурса?
Решение:
Множество элементарных событий: N=80
A={команда России выступает в третий день}
В третий день выступает : N(A)=(80-8):4=18
N ( A) 18
P( A)
0,225
N
80
Ответ: 0,225

9.

Задача 6. Перед началом первого тура чемпионата по
бадминтону участников разбивают на игровые пары
случайным образом с помощью жребия. Всего в чемпионате
участвует 26 бадминтонистов, среди которых 10 участников из
России, в том числе Руслан Орлов. Найдите вероятность того,
что в первом туре Руслан Орлов будет играть с каким-либо
бадминтонистом из России?
Решение:
Множество элементарных событий: N=25
A={Орлов будет играть с русским}
Русских бадминтонистов : N(A)=9
N ( A) 9
P( A)
0,36
N
25
Ответ: 0,36

10.

Задача 7. В классе 26 человек, среди них два близнеца —
Андрей и Сергей. Класс случайным образом делят на две
группы по 13 человек в каждой. Найдите вероятность того,
что Андрей и Сергей окажутся в одной группе.
Ответ: 0,48

11.

Справочный
материал
Сумма вероятностей всех элементарных событий опыта
равна 1.
Вероятность события А равна сумме вероятностей
элементарных событий, благоприятствующих этому
событию.
Несовместные события – события, которые не
наступают в одном опыте.
Противоположные события – те, которые
состоят из тех и только тех элементарных исходов
опыта, которые не входят в А и обозначаются
А
Р А 1 Р А

12.

Справочный
материал
Объединение событий
А В
- событие, состоящее из элементарных исходов,
благоприятствующих хотя бы одному из
событий А и В.
- Формула сложения вероятностей для
несовместных событий:
Р(А В) Р(А) Р(В)
- Формула сложения вероятностей :
Р А В Р А Р В Р А В

13.

Справочный
материал
Пересечение событий А В - это событие,
состоящее из элементарных исходов,
благоприятствующих обоим событиям А и В.
Независимые события. События А и В называются
независимыми, если
Р ( А В ) Р ( А ) Р ( В )

14.

Задача 8. Из районного центра в деревню ежедневно
ходит автобус. Вероятность того, что в понедельник в
автобусе окажется меньше 20 пассажиров, равна 0,94.
Вероятность того, что окажется меньше 15 пассажиров,
равна 0,56. Найдите вероятность того, что число
пассажиров будет от 15 до 19.
Решение:
А: Число пассажиров меньше 20
P(A)=0,94
А1: Число
пассажиров
меньше
15
Р(А1)=0,56
0,94-
А2: Число
пассажиров
от 15 до
19
Р(А2)=?
Ответ: 0,48

15.

Задача 9. В торговом центре два одинаковых автомата
продают кофе. Вероятность того, что к концу дня в автомате
закончится кофе, равна 0,3. Вероятность того, что кофе
закончится в обоих автоматах, равна 0,12. Найдите
вероятность того, что к концу дня кофе останется в обоих
автоматах.
Решение.
1. Определим события:
А={кофе закончится в первом
автомате}
В={кофе закончится во втором
автомате}
По условию задачи Р(А)=Р(В)=0,3 и
P ( A B ) 0 ,12
2. По формуле сложения вероятностей
найдем вероятность события:

16.

Задача 9. В торговом центре два одинаковых автомата продают
кофе. Вероятность того, что к концу дня в автомате закончится
кофе, равна 0,3. Вероятность того, что кофе закончится в обоих
автоматах, равна 0,12. Найдите вероятность того, что к концу
дня кофе останется в обоих автоматах.
A B {кофе закончится хотя бы
в одном из автоматов}
Р( А В)
=Р(А)+Р(В) – Р( А В) =
=0,3+0,3-0,12=0,48
Следовательно, вероятность
противоположного события «кофе
останется в обоих автоматах»
равна 1-0,48=0,52.
Ответ. 0,52

17.

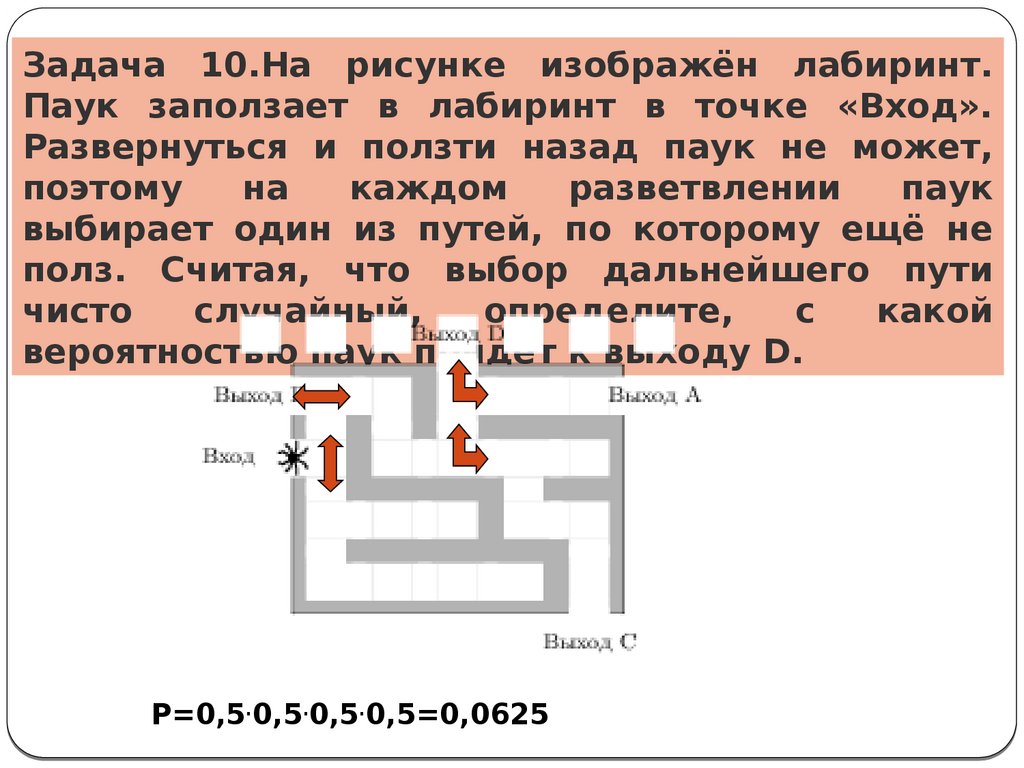
Задача 10.На рисунке изображён лабиринт.
Паук заползает в лабиринт в точке «Вход».
Развернуться и ползти назад паук не может,
поэтому
на
каждом
разветвлении
паук
выбирает один из путей, по которому ещё не
полз. Считая, что выбор дальнейшего пути
чисто
случайный,
определите,
с
какой
вероятностью паук придёт к выходу D.
Р=0,5.0,5.0,5.0,5=0,0625

18.

Задача 11. В магазине стоят два платежных автомата.
Каждый из них может быть неисправен с вероятностью 0,05
независимо от другого автомата. Найдите вероятность того,
что хотя бы один автомат исправен.
Решение.
1. Найдем вероятность противоположного
события:
={оба автомата неисправны }
А
2. Для этого используем формулу
умножения вероятностей независимых
событий: Р ( А ) 0,05 0,05 0,0025
3. Значит вероятность события
А={хотя бы один автомат исправен} равна:
Р(А)=1 – 0,0025=0,9975.
Ответ. 0,9975

19.

Задача 12.Агрофирма закупает куриные яйца в двух
домашних хозяйствах. 40% яиц из первого хозяйства —
яйца высшей категории, а из второго хозяйства — 20%
яиц высшей категории. Всего высшую категорию
получает 35% яиц. Найдите вероятность того, что яйцо,
купленное у этой агрофирмы, окажется из первого
хозяйства.
40
%
35%
20
A={яйцо, купленное у агрофирмы,%
окажется из 1-го хозяйства.}

20.

40
%
Пусть Р(А)=х
35%
20
A={яйцо, купленное у агрофирмы,%
окажется из 1-го хозяйства.}
В={яйцо, купленное у агрофирмы, окажется из 2-го хозяйства.}
Р(В)=1-х
А1={яйцо высшей категории, купленное у агрофирмы, окажется
из 1-го хозяйства.}
Р(А1)=0,4.X
А2={яйцо высшей категории, купленное у агрофирмы, окажется
из 2-го хозяйства.}
Р(А2)=0,2(1-.X)
Из уравнения 0,4х+0,2(1-х)=0,35
получим х=0,75

21.

Задача13.В магазине три продавца. Каждый из них занят с
клиентом с вероятностью 0,3. Найдите вероятность того, что
в случайный момент времени все три продавца заняты
одновременно (считайте, что клиенты заходят независимо
друг от друга).
Ответ: 0,027

22.

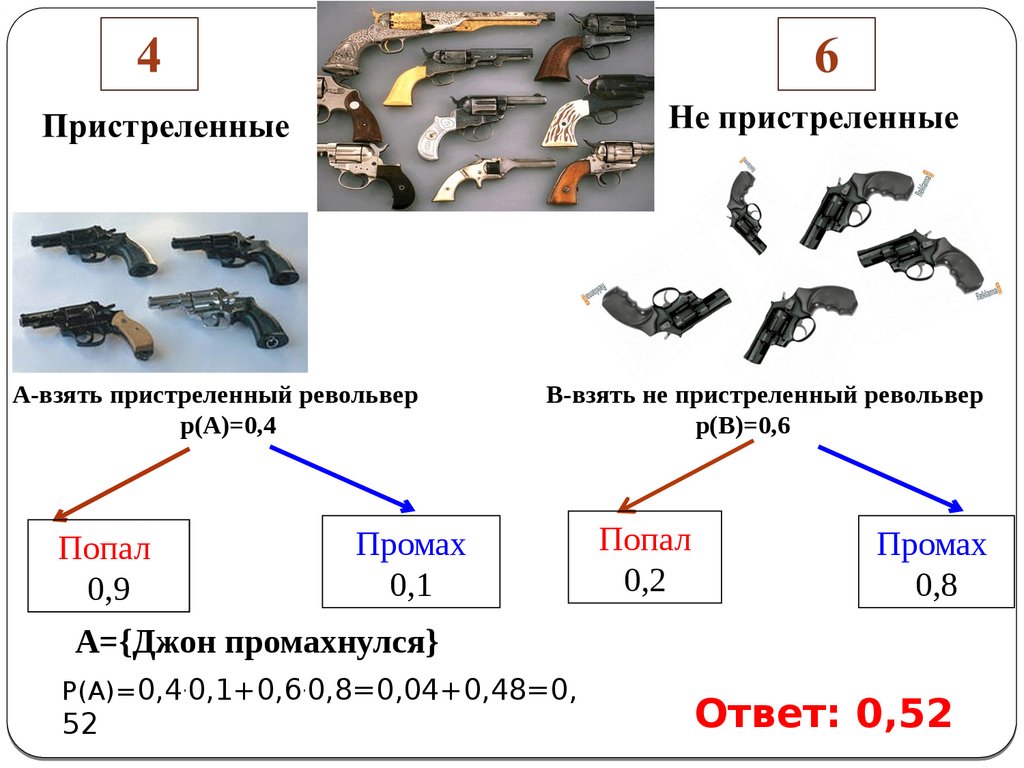
Задача 14.Ковбой Джон попадает в муху на стене с
вероятностью 0,9, если стреляет из пристрелянного
револьвера. Если Джон стреляет из не пристрелянного
револьвера, то он попадает в муху с вероятностью 0,2. На
столе лежит 10 револьверов, из них только 4 пристрелянные.
Ковбой Джон видит на стене муху, наудачу хватает первый
попавшийся револьвер и стреляет в муху. Найдите
вероятность того, что Джон промахнётся.
4
Пристреленные
6
Не пристреленные

23.

А-взять пристреленный револьвер
р(А)=0,4
Попал
0,9
В-взять не пристреленный револьвер
р(В)=0,6
Промах
0,1
Попал
0,2
Промах
0,8
A={Джон промахнулся}
P(A)=0,4.0,1+0,6.0,8=0,04+0,48=0,
52
Ответ: 0,52

24.

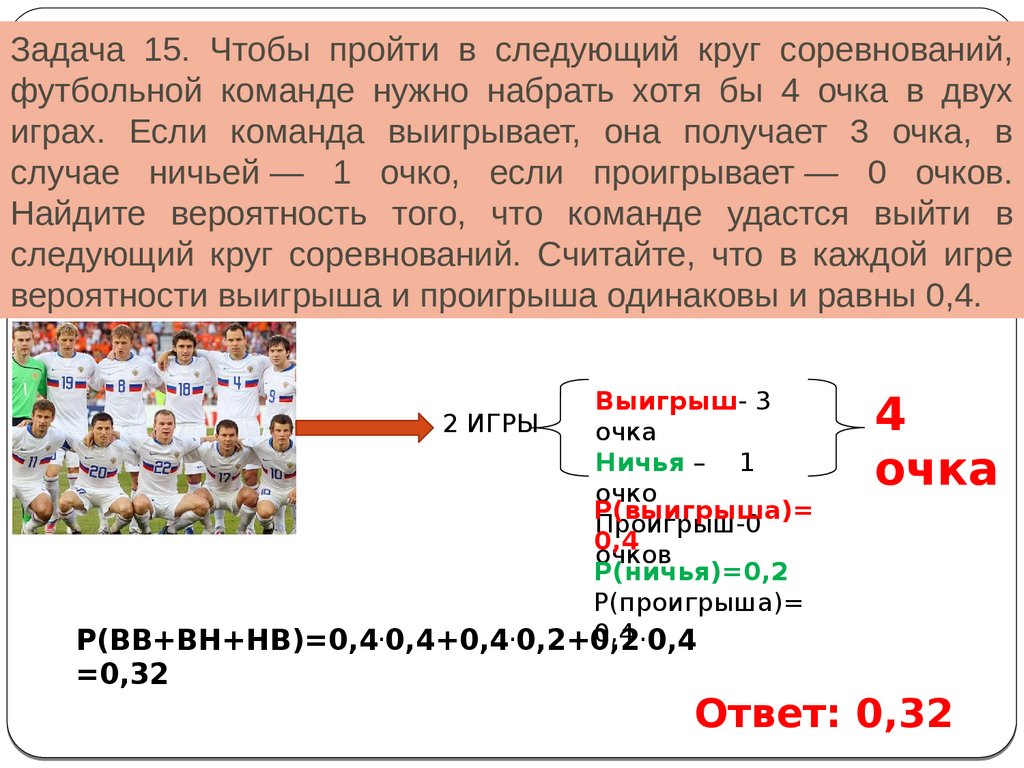
Задача 15. Чтобы пройти в следующий круг соревнований,
футбольной команде нужно набрать хотя бы 4 очка в двух
играх. Если команда выигрывает, она получает 3 очка, в
случае ничьей — 1 очко, если проигрывает — 0 очков.
Найдите вероятность того, что команде удастся выйти в
следующий круг соревнований. Считайте, что в каждой игре
вероятности выигрыша и проигрыша одинаковы и равны 0,4.
Выигрыш- 3
очка
Ничья – 1
очко
Р(выигрыша)=
Проигрыш-0
0,4
очков
Р(ничья)=0,2
Р(проигрыша)=
0,4 .0,4
Р(ВВ+ВН+НВ)=0,4.0,4+0,4.0,2+0,2
2 ИГРЫ
=0,32
4
очка
Ответ: 0,32

25.

Задача 16. Всем пациентам с подозрением на гепатит делают анализ крови.
Если анализ выявляет гепатит, то результат анализа называется
положительным. У больных гепатитом пациентов анализ даёт
положительный результат с вероятностью 0,9. Если пациент не болен
гепатитом, то анализ может дать ложный положительный результат с
вероятностью 0,01. Известно, что 5% пациентов, поступающих с
подозрением на гепатит, действительно больны гепатитом. Найдите
вероятность того, что результат анализа у пациента, поступившего в
клинику с подозрением на гепатит, будет положительным.
Больных
5%
0,9
Здоровых
Здоровых
95%
95%
0,01
Р(Анализ
положительный)=0,05.0,9+0,95.0,01=0,0545
Ответ:

26.

О
Б
И
!
С
Е
А
И
А
П
З
Н
С
А
М
И
Н
В