Системы счисления

1.

Системы
счисления
ProfExam

2.

Система счисления это знаковая система, в которой числа
записываются по определенным
правилам с помощью символов
некоторого алфавита, называемых
цифрами.
Цифры – это знаки, используемые при
записи чисел. Сами знаки составляют
алфавит системы счисления.

3.

Системы счисления
(классификация)
Непозиционные
Системы счисления,
в которых каждой
цифре соответствует
величина,
не зависящая от её
места в записи числа
Позиционные
Системы счисления,
в которых количественное
значение цифры зависит
от ее положения (позиции)
в числе (в
последовательности цифр,
изображающей число)
Древнегреческая
Древнегреческая,
Римская.
Десятичная, двоичная и т.д.

4.

Позиционные системы счисления
В позиционных системах счисления количественное
значение цифры зависит от ее позиции в числе.
Позиция цифры в числе называется разрядом.
Наиболее распространенной позиционной системой
счисления является десятичная.
Например в числе 555
5 сотен, 5 десятков, 5 единиц
55510=5*102 + 5*101 + 5*100
Алфавит десятичной системы счисления 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Основание системы 10

5.

Двоичная система счисления
Двоичная система счисления является основной
системой представления информации памяти
компьютера.
Алфавит двоичной системы счисления
Основание системы 2
1012
1*22 + 0*21 + 1*20
0и1

6.

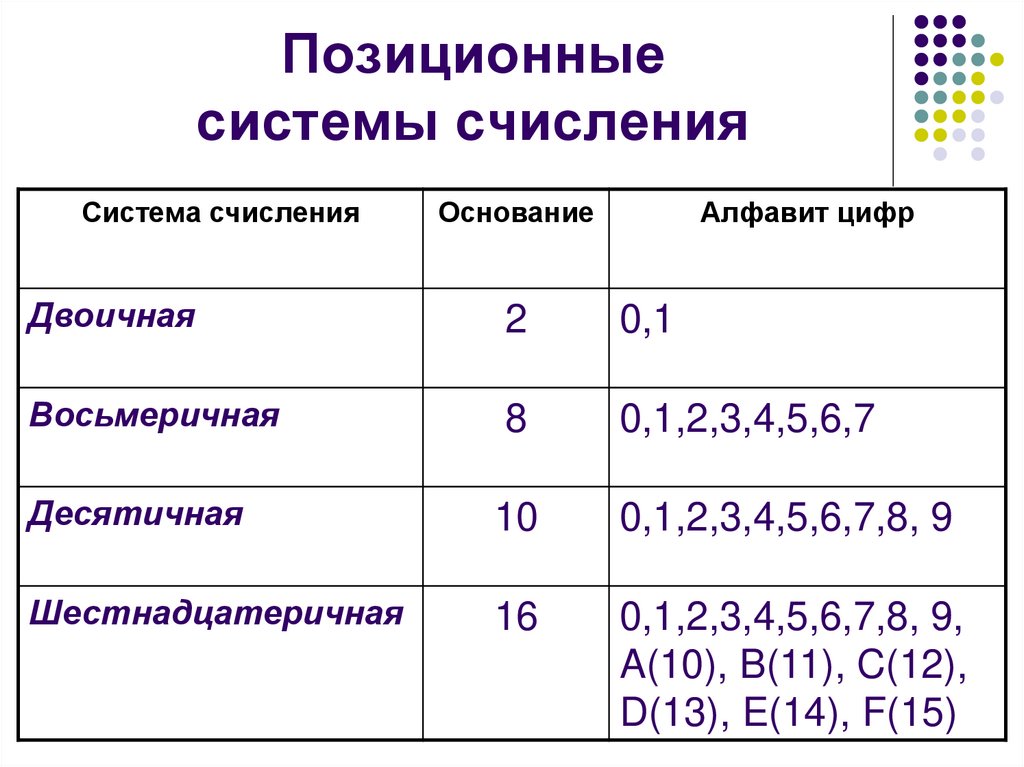
Позиционные
системы счисления
Система счисления
Основание
Алфавит цифр
Двоичная
2
0,1
Восьмеричная
8
0,1,2,3,4,5,6,7
Десятичная
10
0,1,2,3,4,5,6,7,8, 9
Шестнадцатеричная
16
0,1,2,3,4,5,6,7,8, 9,
A(10), B(11), C(12),
D(13), E(14), F(15)

7.

Правило перевода
из разных систем счисления
в десятичную:
необходимо записать число
в развернутой форме
и вычислить его значение
110112=1*24 + 1*23 + 0*22 + 1*21 + 1*20
= 1*16+1*8 + 0*4 + 1*2 + 1*1 = 2710
338 =3*81+3*80=3*8+3*1=24+3=2710
1В16=1*161+В*160=1*16+11*1=2710

8.

Перевод чисел из десятичной
системы счисления
в другие системы
Способ деления: десятичное число делим на
основание системы – получаем частное и
остаток. Остаток запоминается. Частное
вновь делим на основание системы – опять
получаем частное и остаток. И так
продолжаем, пока частное не станет меньше
основания системы.
После чего записываем последнее частное и
все остатки в обратном порядке – полученное
число и есть результат перевода из
десятичной системы счисления в искомую.

9.

Перевод числа из десятичной системы счисления
в двоичную систему счисления.
26 / 2
0 13 / 2
1 6/2
результат деления
0 3/2
110102
1 1
Перевод числа из десятичной системы счисления
в восьмеричную.
26 / 8
2
3 результат деления 328
Перевод числа из десятичной системы счисления в
шестнадцатеричную.
26 / 16
10 1
А
результат деления 1А16

10.

Перевод чисел из двоичной
системы счисления в
восьмеричную.
1010012 1012 0012
1*22 + 0*21 + 1*20 0*22 + 0*21 +1*20=518
Двоичные
триады
Восьмеричные
цифры
000 001 010 011 100 101 110 111
0
1
2
1010012 1012 0012 =518
5
1
3
4
5
6
7

11.

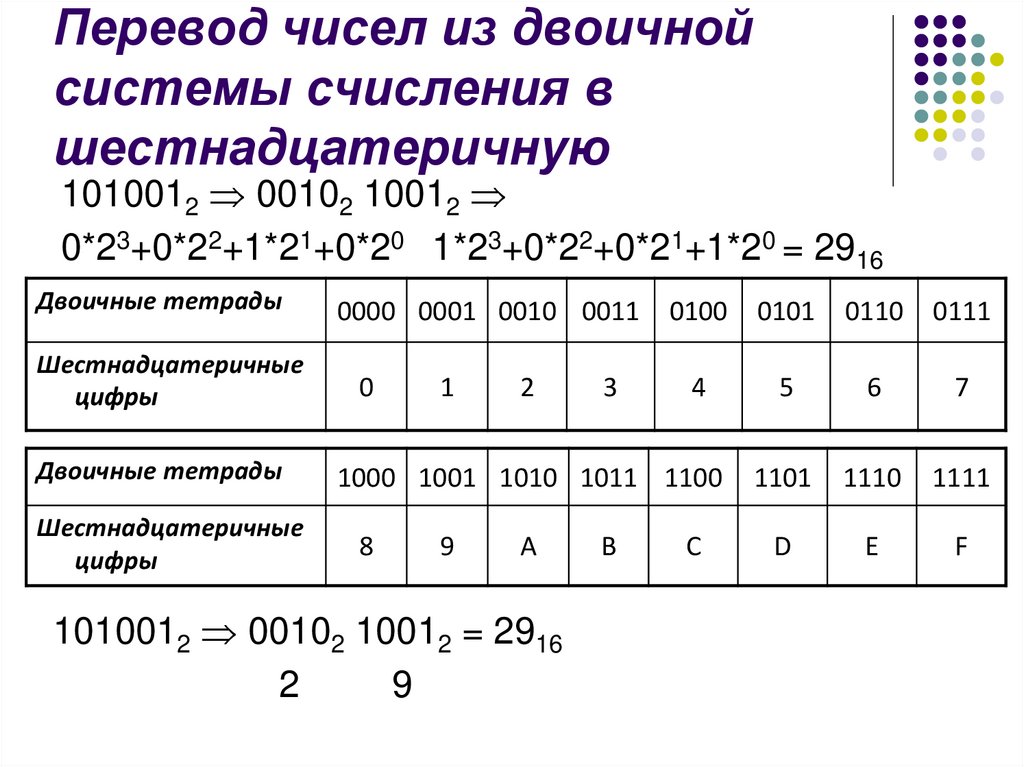
Перевод чисел из двоичной
системы счисления в
шестнадцатеричную
1010012 00102 10012
0*23+0*22+1*21+0*20 1*23+0*22+0*21+1*20 = 2916
Двоичные тетрады
Шестнадцатеричные
цифры
Двоичные тетрады
Шестнадцатеричные
цифры
0000 0001 0010 0011
0
1
2
3
0100
0101
0110
0111
4
5
6
7
1101
1110
1111
D
E
F
1000 1001 1010 1011 1100
8
9
А
1010012 00102 10012 = 2916
2
9
В
С

12.

Задачи на закрепление.
Переведите в десятичную систему
двоичное число 1010012
Вычислите: 101010102 – 2528 + 716. Ответ
запишите в десятичной системе
счисления.
Сколько существует натуральных чисел x,
для которых выполнено неравенство
110111002 < x < DF16?

13.

Вопросы и задания на дом
1.
2.
3.
4.
5.
6.
Чем отличаются позиционные системы счисления от
непозиционных?
Может ли в качестве цифры использоваться символ буквы?
Переведите в десятичную системы счисления из
Двоичной: 1010, 11101, 10111
Восьмеричной: 7, 22, 17
Шестнадцатеричной: BF, 9C, 2A
Переведите из десятичной системы счисления в двоичную,
восьмеричную и шестнадцатеричную числа: 67, 77
Переведите из двоичной системы счисления в восьмеричную
и шестнадцатеричную системы числа:1111, 1010101.
Сравните числа, выраженные в различных системах
счисления: 11012 и D16; 358 и 1С16