Звездчатые многогранники

1.

2.

«Математика владеет не только
истиной, но и высшей красотой красотой отточенной и строгой,
возвышенно чистой стремящейся к
подлинному совершенству, которое
свойственно лишь величайшим
образцам искусства»
Бертран Рассел.

3.

Введение:
Математика – это не только стройная система
законов, теорем, задач, но и уникальное средство
познания красоты. А красота многогранна и
многолика. Она выражает целесообразность
устройства мира, подтверждает универсальность
математических закономерностей. Изучая
математику, мы открываем всё новые и новые
слагаемые красоты, приближаясь к пониманию, а
затем и к созданию красоты и гармонии. Когда
раскрывается эффективность применения
математических методов в различных областях, не
ущемляется роль математики, не подменяется
другими предметами, а, наоборот, повышается
интерес к предмету, выявляется высокое значение
математики, процесс познания её делается
увлекательным

4.

Цель работы:
• - Расширить знания о звёздчатых
многогранниках.
• -Исследовать способы изготовления
различных моделей звёздчатых
многогранников.
• -Увеличение интереса к геометрии;
• -Развитие логического мышления.

5.

Актуальность:
Теория многогранников не является одним лишь
достоянием прошлого. И сейчас, спустя два
тысячелетия, многих привлекает лежащее в их основе
эстетическое начало. О том, что они не утратили свою
притягательность и поныне, весьма убедительно
свидетельствует и их применение в науке, искусстве,
архитектуре. Они встречаются в живой и неживой
природе, в окружающем нас мире. Кроме того, теория
многогранников является современным разделом
математики, она, имеет большое значение как для
теоретических исследований по геометрии, так и для
практических приложений в других разделах
математики. Таким образом, данная тема актуальна, а
знания по данной проблеме являются важными для
современного общества

6.

Звездчатые многогранники
Кроме правильных и полуправильных
многогранников, красивые формы имеют, так
называемые, звездчатые многогранники.
Первые два были открыты И. Кеплером, а два
других почти 200 лет спустя построил Л.
Пуансо (1777-1859) .
Именно поэтому правильные звездчатые
многогранники называют телами Кеплера –
Пуансо. Они получаются из правильных
многогранников продолжением их граней
или ребер.

7.

Малый звездчатый додекаэдр
Малый звездчатый додекаэдр - правильный звездчатый многогранник .
Состоит из двенадцати граней, грань малого звездчатого додекаэдра правильная пятиконечная звезда, пентаграмма. Каждая вершина малого
звездчатого додекаэдра - вершина пяти пентаграмм сходящихся в ней.
Малый звездчатый додекаэдр можно получить продолжив грани
правильного выпуклого додекаэдра до их первого пересечения.
Основные характеристики:
Тип - Правильный звездчатый
многогранник
Грань - Правильная
пятиконечная звезда
(пентаграмма)
Граней - 12
Граней при вершине - 5
Вершин - 12
Ребер - 30

8.

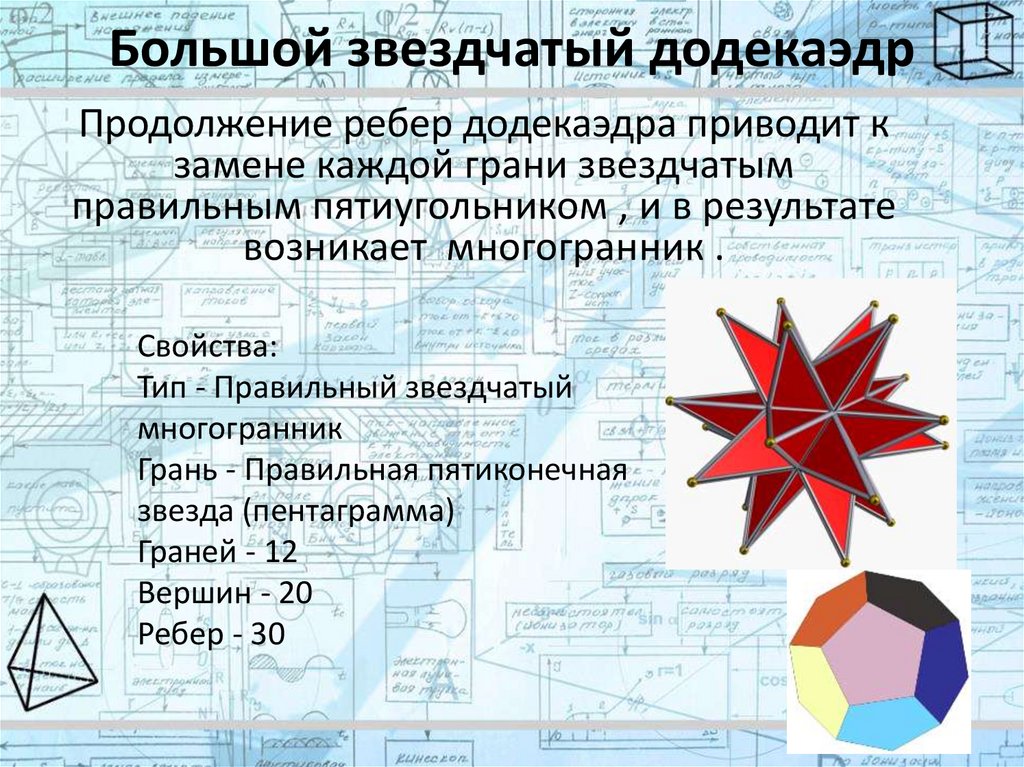
Большой звездчатый додекаэдр
Продолжение ребер додекаэдра приводит к
замене каждой грани звездчатым
правильным пятиугольником , и в результате
возникает многогранник .
Свойства:
Тип - Правильный звездчатый
многогранник
Грань - Правильная пятиконечная
звезда (пентаграмма)
Граней - 12
Вершин - 20
Ребер - 30

9.

Звёздчатый икосаэдр
Звездчатая форма икосаэдра
состоит из 20 частей, каждая
часть представляет собой
невысокую треугольную
пирамиду без основания

10.

Звездчатый октаэдр
Звёздчатый октаэдр можно было бы
признать правильным
многогранником, так как все его
грани - правильные треугольники
одинакового размера и все углы
между ними равны.

11.

Многогранное оригами

12.

Заключение
Многогранники – интересные тела геометрии,
имеющие разнообразные свойства. По
внешнему признаку имеют различия, но они
объединены в одну группу, и объединяет их
великая наука – геометрия. «Земные звезды»
сложны по своим особенностям и свойствам, но
именно сложность и загадочность этих тел и
привлекает различных людей изучать их.
Математическая безупречность линий ни чуть
не ограничивает творчество, фантазию людей.

13.

Список литературы:
1)М. Венниджер «Модели
многогранников».Москва «Мир» 1974г.
Использованные ресурсы:
https://ru.wikipedia.org/wiki/Звёздчатый_многогранник
http://dic.academic.ru/dic.nsf/ruwiki/105329