В стране целых и рациональных чисел

1. Тема: «В стране целых и рациональных чисел»

« Числа не управляют миром, но они
показывают, как управлять им».
( И. Гёте).
Подготовила:
Учитель математики
МБОУ-СОШ № 14 г.
Армавира
Гаёкова Екатерина
Сергеевна

2.

Для счета предметов используются числа , которые
называются натуральными. Для обозначения
множества натуральных чисел употребляется
буква N -первая буква латинского слова Naturalis,
«естественный», «натуральный»
Натуральные числа, числа им противоположные
и число нуль, образуют множество целых чисел,
которое обозначается Z - первой буквой
немецкого слова Zahl - «число».
m
Множество чисел, которое можно представить в виде
,
называется множеством рациональных чисел и обозна- n
чается- Q первой буквой французского слова Quotient
- «отношение».

3.

Цель занятия:
систематизировать
знания о целых
рациональных числах;
познакомиться с
историей возникновения
целых и рациональных
чисел;
выделить общее свойство
рациональных чисел.

4.

Натуральные числа возникли в силу
необходимости вести счет любых
предметов.
Натуральные числа несут ещё
другую функцию –
характеристика порядка предметов,
расположенных в ряд.
1
2
3
4
5
6
7
8 9 10…

5.

О натуральном,в смысле естественном,
ряде чисел говорится во «Введении в
арифметику» греческого математика
( неопифагорийца) Никомаха из Геразы.
В современном смысле
понятие и термин
«Натуральное число»
встречается у французского
философа и математика
Ж.Даламбера (1717-1783)

6.

Натуральные числа
1, 2, 3, 4, 5, 6...
n - натуральное
n∈ N
Сумма и произведение натуральных
чисел есть число натуральное.

7.

Дроби естественно возникли при решении
задач о разделе имущества, измерении
земельных участков, исчислении времени.

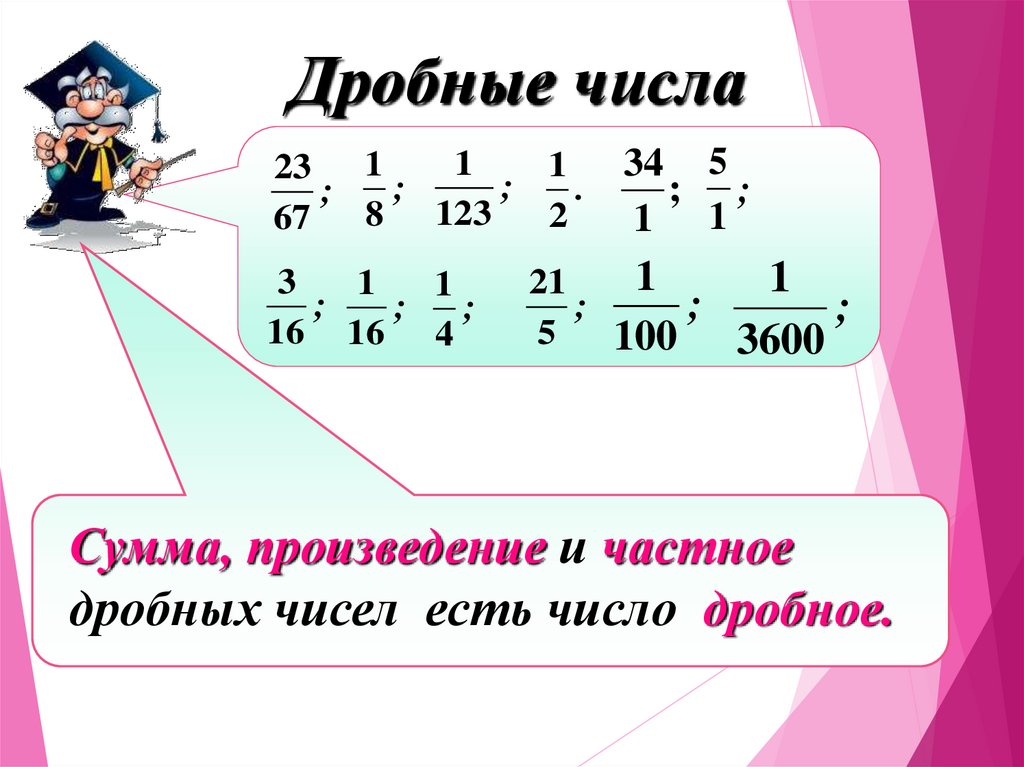
8.

Дробные числа
1
1
1
23
;
;
.
;
8 123
2
67
3
1
1
;
;
;
16 16 4
34 5
; ;
1 1
1
21
;
;
5
100
1
;
3600
Сумма, произведение и частное
дробных чисел есть число дробное.

9.

1) доли или единичные дроби,
у которых числитель единица,
знаменателем же может быть
любое целое число; 1 ; 1 ; 1 ; 1 ;
16
8
4
123
2) дроби систематические, у которых
числителями могут быть любые числа,
знаменателями же – только числа некоторого
частного вида, например,
1
1
1
;
;
;
степени десяти или шестидесяти; 60 3600 100
3)дроби общего вида, у которых числители и
знаменатели могут быть любыми числами.

10.

Десятичные дроби в XV веке
ввел самаркандский ученый
ал - Каши.
Ничего, не зная об открытии ал – Коши,
десятичные дроби открыл второй раз,
приблизительно через 150 лет, после него,
фламандский ученый математик и инженер
Симон Стевин в труде «Децималь» (1585 г).

11.

Понятие отрицательных чисел
возникло в практике решения
алгебраических уравнений.
Отрицательные числа трактовались
так же как долг при финансовых и
бартерных расчетах.

12.

Отрицательные числа ввели
в математический обиход
Михаэль Штифель (1487—1567)
в книге «Полная арифметика» (1544),
и Никола Шюке (1445—1500)его работа была обнаружена в 1848
году.

13.

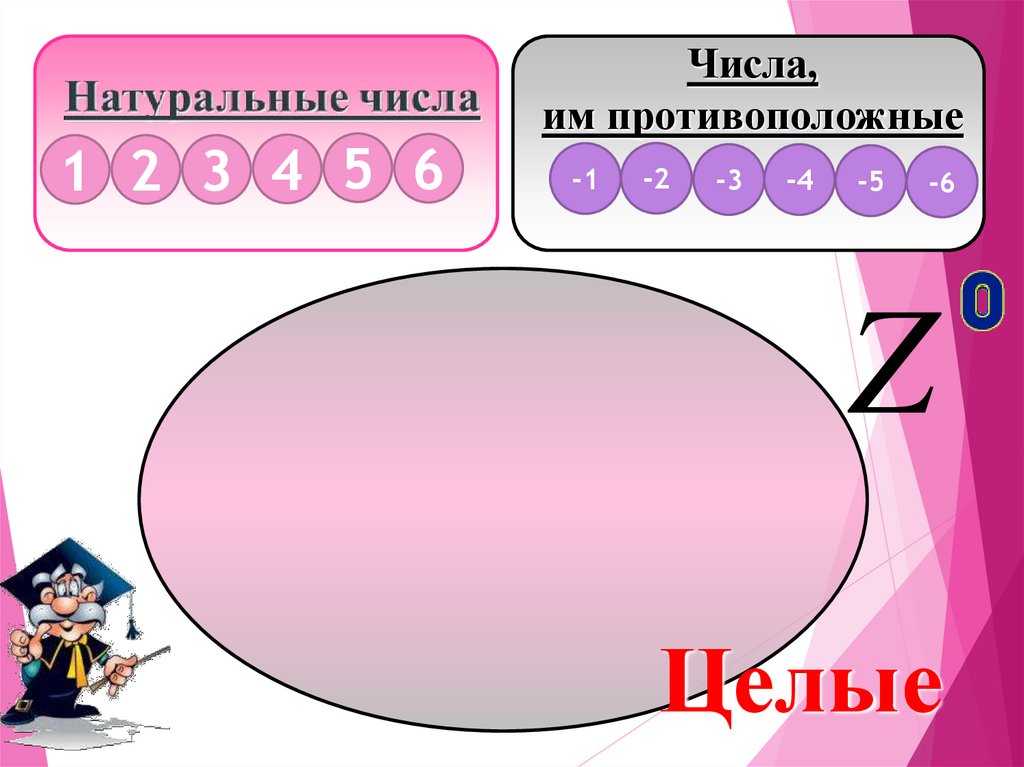
1 2 3 4 5 6
Числа,
им противоположные
-1
-2
-3
-4
-5
-6
Z
Целые

14.

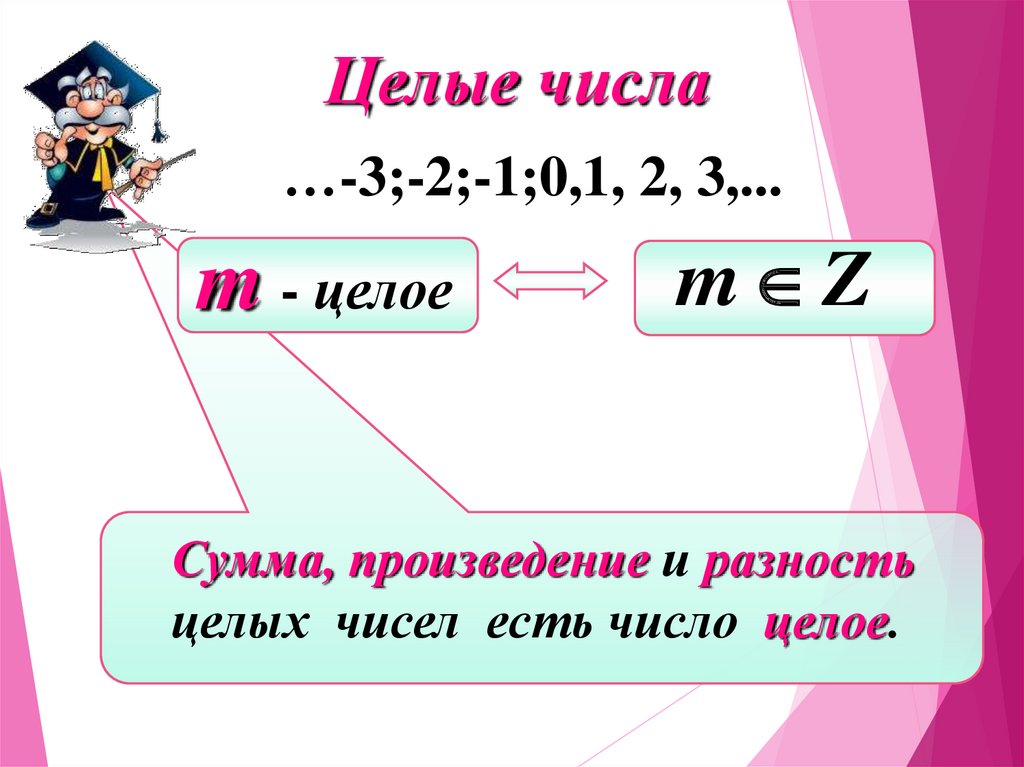
Целые числа
…-3;-2;-1;0,1, 2, 3,...
m - целое
m Z
Сумма, произведение и разность
целых чисел есть число целое.

15.

Целые числа
Дробные числа
2/7
2
5
7,1
3,2
0,(2)
0,1
1
0
-4
9
58
10
Q
Рациональные

16.

Рациональные числа
r - рациональное
r Q
Сумма, произведение, разность и
частное рациональных чисел есть
число рациональное.

17. Отношения между множествами натуральных, целых и рациональных чисел наглядно демонстрирует геометрическая иллюстрация – круги

Эйлера.
Q-
рациональные числа
ZЛеонард Эйлер
жил в России в
середине XYΙΙΙ
века и внес
большой вклад
в развитие
математики.
N-
целые числа
натуральные числа

18.

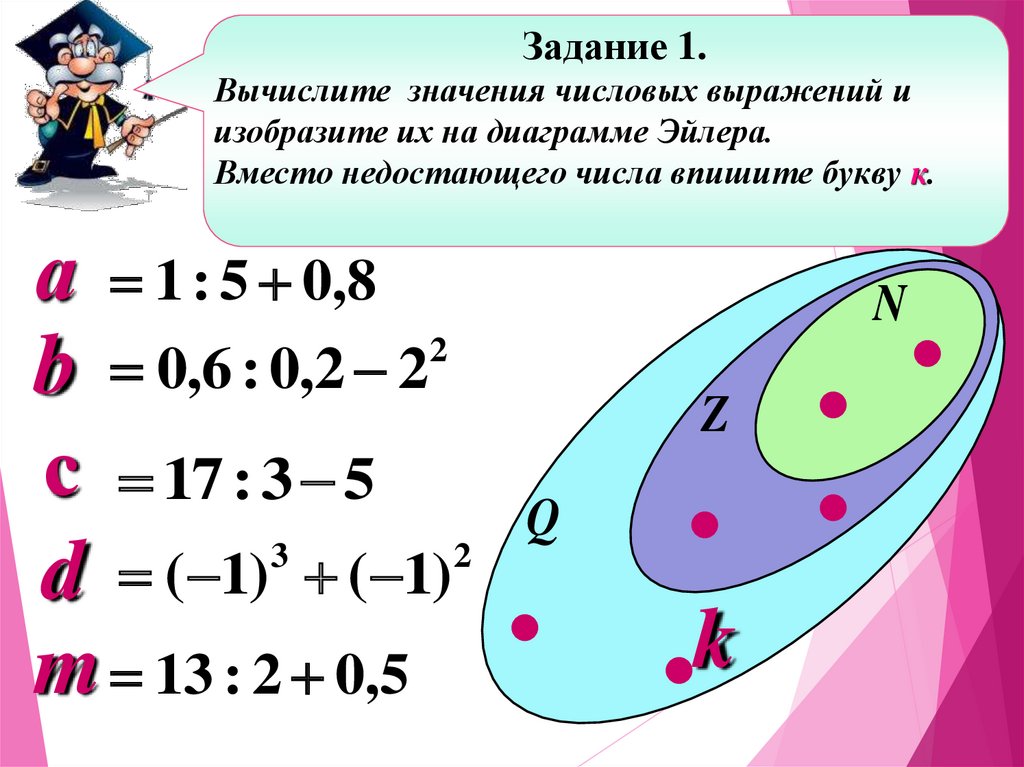
Задание 1.
Вычислите значения числовых выражений и
изобразите их на диаграмме Эйлера.
Вместо недостающего числа впишите букву к.
а 1 : 5 0,8
2
b 0,6 : 0,2 2
с 17 : 3 5
3
2
d ( 1) ( 1)
m 13 : 2 0,5
N
Z
Q
k

19.

Задание2. Замените данные
рациональные числа
десятичными дробями.
1
2
0,5
1
0,2
5
1
1
0,125
0 ,333...
8
3
1
0,25
4
2
0,4
5
3
0,375
8
2
0 ,666...
3
3
0,75
4
3
0,6
5
5
0,625
8
1
0 ,1666..
6

20. Дробные числа

Десятичные дроби
дроби со знаменателем
0,1
0,03
0,125984
10
n
15,0849
Преобразование обыкновенной дроби в
десятичную:
1
1 : 2 0 ,5
2
2
2 : 2 5 0 ,0 8
25

21.

Задание 3. Преобразование обыкновенной дроби в
десятичную
1
0 , 333 3 3 3 3 3 3 ... 0 , 3 Бесконечные
3
5
десятичные
0 ,555 5 5 5 5 ... 0 , 5
9
периодические
7
0 ,663
3 6 3 6 3 6 3 ... 0 , 63 дроби
11
2
0 ,2 8 5 7 1 4 2 6 8 7 1 4 ... 0 , 2 8 5 7 1 4
7
период

22.

Задание 4. Прочитайте дроби:
1) 0,(2)
2) 2,(21)
4) -3,0(3)
5) -0,1(6)
3) 1,(1)
6) 12,45(7)
чисто периодические
смешанные периодические

23.

Задание 5. Докажите, что равенства верны:
2
а) 0,222…=
9
9
б) 0,8181…=
11
7
в) 0,4666 …=
15

24.

Чтобы обратить чисто периодическую дробь
в обыкновенную, нужно в числителе обыкновенной
дроби поставить число,
образованное из цифр, стоящих в периоде,
а в знаменателе – написать цифру 9 столько раз,
сколько цифр в периоде.
0,(2)=
2
1 цифра
9
0,(81)=
81
2 цифры
99
9
11

25.

Чтобы обратить смешанную периодическую дробь
в обыкновенную, нужно в числителе обыкновенной дроби
поставить число, равное разности числа, образованного
цифрами, стоящими после запятой до начала второго
периода, и числа, образованного из цифр, стоящих после
запятой до начала первого периода;
а в знаменателе написать цифру 9 столько раз, сколько
цифр в периоде, и со столькими нулями, сколько цифр
между запятой и началом периода.
0,4(6)=
46
1 цифра
1 цифра
90
42 7
90 15

26.

Задание 6.
Проверь соседа
72
8
8
1) 1, (72) 1
1 1
99
11
11
912 9
903
301
2) 2,9(12) 2
2
2
990
990
495
128 12
116
29
3) 1,12(8) 1
1
1
900
900
225

27. Графический диктант

1) 2016 Z
1
2) 0 ,33
3
3) любое целое является рациональным
3
4)
0 ,375
8
4
5) 1 ,1 36 1
11
6) любое целое число является натуральным
7) любое рациональное число можно записать в виде конечной или
бесконечной периодической дроби
8) сумма, разность, произведение и частное рациональных чисел есть число
рациональное
9) (- 37,4 - 26,6) : (0,1) - натуральное
10) Q - обозначение множества рациональных чисел.

28.

да
нет
Проверь себя
МОЛОДЦЫ
!

29.

30. Домашнее задание:

§
1, изучить материал § 2.
В тетрадях: № 2-7

31. СПАСИБО ЗА ВНИМАНИЕ!

32.

Ресурсы интернета:
1) http://www.librus.ru/childrens-corner/scientifically-cognitiveliterature
2) /5676-mir-chisel.html;
3) http://odur.let.rug.nl/magazijn/decennia/1745-1754_45.htm;
4) http://project-gym6.narod.ru/1/62/euler.htm;
5) http://sferica.by.ru/history/pi.html;
6) http://www.peoples.ru/science/mathematics/simon_stev
in/;
7) http://www.proshkolu.ru/user/galrybo/file/455559/;
8) http://www.15a20.com.mx/images/sections/thumbs/thu
mb_7312558.jpg;
9) http://gr-matem.narod.ru/;
10) http://www.i-u.ru/biblio/archive/depman_mir/01.aspx