Похожие презентации:
Построение треугольника по трем сторонам
1.
Оленникова Т.Н.учитель математики ГБОУ школы № 413
2.
3.
В Атлантическом океане есть место, по форменапоминающее геометрическую фигуру, о которой
мы
сегодня
будем
говорить.
Это
место,
расположенное между Бермудскими островами,
государством Пуэрто-Рико, полуостровом Флорида и
называется
“бермудским треугольником”.
А ещё его называют “дьявольский треугольник”,
“треугольник
проклятых”.
Загадочность
его
заключается в том, что в нём бесследно исчезают
корабли и самолёты. Природа “бермудского
треугольника” остаётся тайной и по сей день.
4.
ВА
В
А
С
С
5.
Построение треугольникаПостроить треугольник АВС
со сторонами 5 см, 3 см и 4 см
Цель:
Научиться строить треугольник по трем
сторонам.
6.
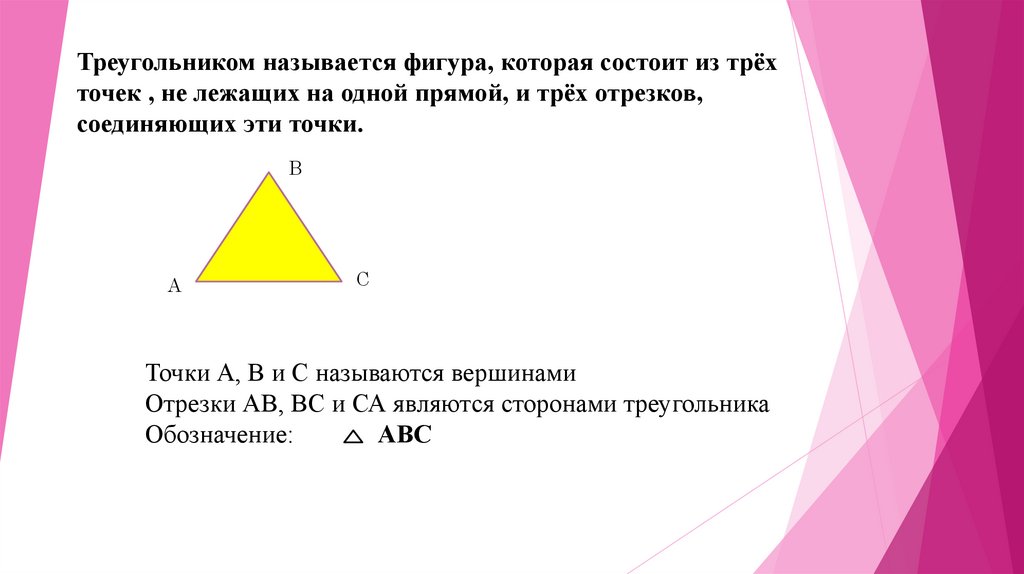
Треугольником называется фигура, которая состоит из трёхточек , не лежащих на одной прямой, и трёх отрезков,
соединяющих эти точки.
В
А
С
Точки А, В и С называются вершинами
Отрезки АВ, ВС и СА являются сторонами треугольника
Обозначение:
АВС
7.
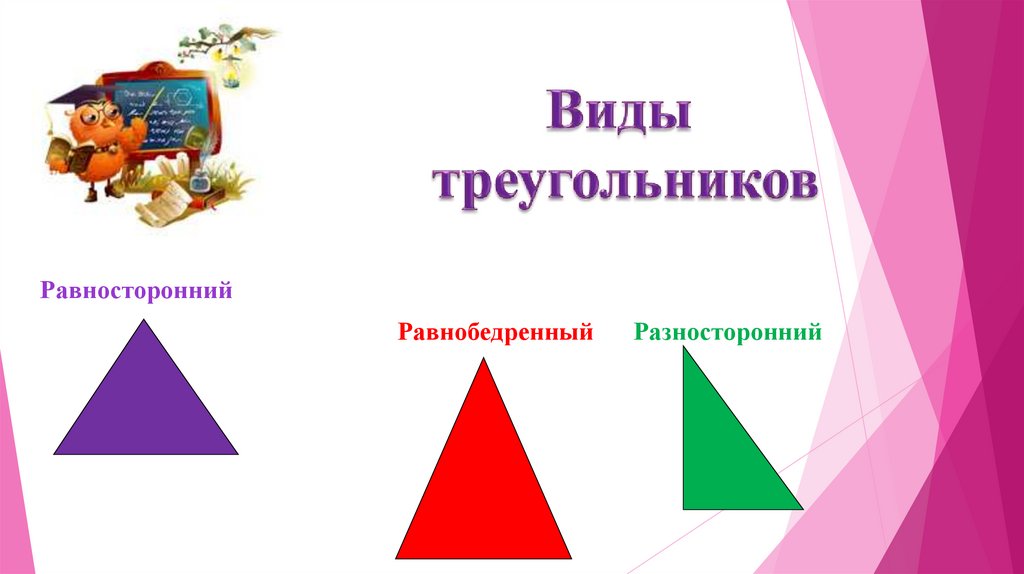
РавностороннийРавнобедренный
Разносторонний
8.
Треугольник – “жесткая” фигура. Если заданы три егостороны, то форму треугольника уже изменить нельзя,
не разрушив его. Это свойство широко используется на
практике
1) Делая садовую калитку обязательно прибивают планку/доску/,
иногда две планки, чтобы получить треугольники. Это придаёт
калитке прочность, иначе её перекосит.
2) Стропила зданий имеют вид треугольников. Это придаёт
крепость и устойчивость.
3) При строительстве любых мостов в их конструкциях также
присутствуют треугольники.
Чем больше треугольников в любой конструкции, тем она
прочнее.
9.
В различныхконструкциях:
Телебашня в Токио
10.
Построить треугольник АВСсо сторонами 5 см, 3 см и 4 см
1.
Строим отрезок АС = 5 см.
2.
Строим окружность с центром в точке А и радиусом 3 см.
3.
Строим окружность с центром в точке С и радиусом 4 см.
4.
Точку пересечения этих окружностей обозначим буквой В – это
третья вершина искомого треугольника.
5.
Проводим отрезки АВ и ВС. Получили
АВС.
11.
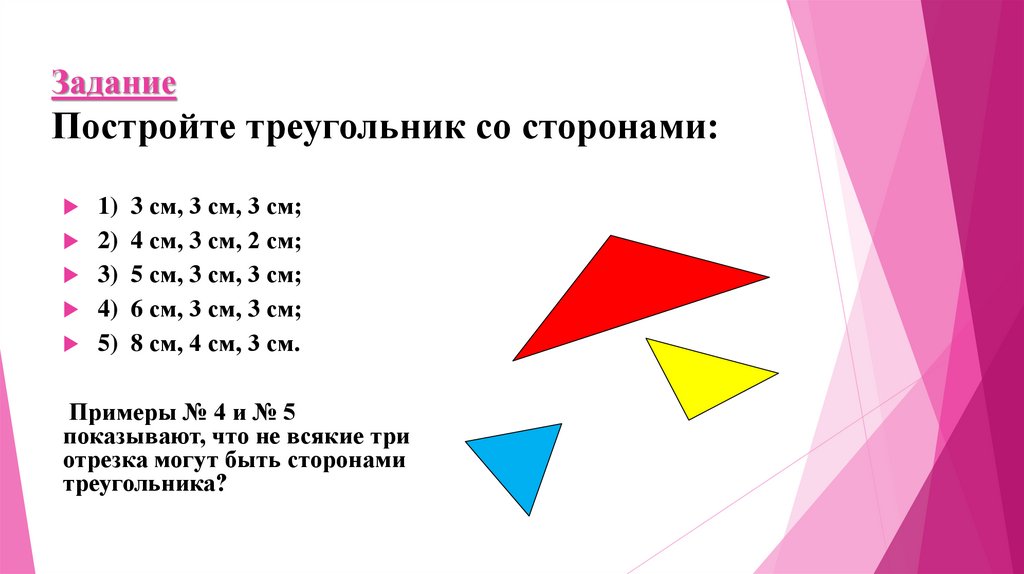
ЗаданиеПостройте треугольник со сторонами:
1)
2)
3)
4)
5)
3 см, 3 см, 3 см;
4 см, 3 см, 2 см;
5 см, 3 см, 3 см;
6 см, 3 см, 3 см;
8 см, 4 см, 3 см.
Примеры № 4 и № 5
показывают, что не всякие три
отрезка могут быть сторонами
треугольника?
12.
Неравенство треугольникаЛюбая сторона треугольника
меньше суммы двух других его
сторон
13.
Задание № 434 (1а)Даны
три отрезка. Как проверить,
можно ли построить треугольник с
такими сторонами?
Любая сторона треугольника меньше
суммы двух других его сторон
Или проверить, что наибольший
отрезок меньше суммы двух других
14.
Практическая работа1 ВАРИАНТ
1. В равнобедренном
треугольнике одна
сторона равна 3,5см, а
другая 7,5см. Какая
сторона является
основанием? Постройте
данный треугольник.
2. Сколько различных
треугольников можно
построить из отрезков
длиною 3см, 4 см, 5 см и
7 см? Ответ обоснуйте.
2 ВАРИАНТ
1. В равнобедренном
треугольнике одна
сторона равна 4 см, а
другая 8 см. Какая
сторона является
основанием? Постройте
данный треугольник.
2. Сколько различных
треугольников можно
построить из отрезков
длиною 2 см, 3 см, 5 см и
6 см? Ответ обоснуйте.
15.
Ответы1 ВАРИАНТ
1. Основание 3,5 см, боковые
стороны по 7,5см.
2. Можно построить 3 :
3 см, 4 см, 5 см, т.к.
5 < 3 + 4;
4 см, 5 см, 7 см, т.к.
7<4+5;
3 см, 5 см, 7 см, т.к.
7 < 3 + 5.
2 ВАРИАНТ
1. Основание 4 см, боковые
стороны по 8см.
2. Можно построить 2:
2 см, 5 см, 6 см, т.к.
6<2+5;
3 см, 5 см, 6 см, т.к.
6<3+5.
Нельзя со сторонами
2см, 3см и 5см, т.к.
2 см + 3 см = 5 см
16.
17.
Домашнее заданиеПо
учебнику п. 5.3
№ 433, 434 (1б, 2),
439(а) на повторение
18.
Подведение итогов1. Опишите алгоритм построения треугольника по
трем сторонам.
2. Треугольник с любыми ли сторонами можно
построить?
3. В чем состоит неравенство треугольника?















 Математика
Математика








